文章目录
前言
GDS图纸的生成
在半导体微纳加工中,一张精确的GDS图纸是器件制备的起点。一般有下面几种生成方式,
1.代码生成:Matlab和python都可安装编译器,通过编码结构的坐标参数来绘制图纸。适用于阵列规模较大且已知结构排布规律的情况;
2.lumerical FDTD等系列的导出:lumerical 软件可对在其中仿真的超构光栅阵列与光波导进行结构的导出。适用于规模较小且支持在有限时间内完成仿真的结构;
3.直接由图纸编辑软件生成:CWin4和klayout软件可以直接绘制基本结构和阵列,也可以对生成的图纸进行微调。适用于结构排布相对简单的情况;
提示:以下是本篇文章正文内容,下面案例可供参考
一、Matlab绘制GDS图纸的流程
先在Matlab中安装mex编译器
1.运行主文件夹下的makemex
2.提示运行成功后,在Project-New project目录下找到Cell-A-StraightWG,并运行
- 选择自行撰写的代码,生成GDS图纸
(文件:nicolasayotte/MatlabGDSPhotonicsToolbox)
二、Matlab生成GDS图纸的程序
1.整体示例
代码如下(以绘制超构纳米柱阵列为例):
matlab
%% *********************************
% Matlab绘制GDS图纸
clc,clear,close all;
gs = gds_structure('Circle');
load('radii_PC.txt');
radius = radii_PC;
radius = radius*10^9; % 量纲对齐,此前的默认单位为m,这里为nm
[Nx,Ny] = size(radius);
p = 650; % 单位为nm, 为周期数值
Mod_x = mod(Nx,2); % 判断是奇数阵列还是偶数阵列
if Mod_x == 1
x = -(p*(Nx-1)/2);
y = p*((Nx-1)/2);
else
x = -Nx/2*p; % 确定结构的初始中心坐标
y = Nx/2*p;
end
y_start = y; % y的起点坐标
m = 361;
C = zeros(m,2); % 数组:存储局部的圆周坐标
C2 = cell(Nx,Ny); % 元胞:存储每个阵列上的全部坐标
% 按列扫描 *********************
for j = 1:Ny
y = y_start;
for i = 1:Nx
R = radius(i,j);
% 确定了R之后开始确定四周的坐标
for k = 1:m
C(k,1) = R*cos(2*pi*(k-1)/(m-1))+x;
C(k,2) = R*sin(2*pi*(k-1)/(m-1))+y;
end
C1 = bsxfun(@plus,C,[x,y]);
C2{i,j} = C; % 将第一个圆柱的坐标存为C2元胞中的第一个元素
y = y - p; % 垂直平移到下一个结构的中心坐标
end
x = x + p; % 水平平移到下一个结构的中心坐标
end
gs(end+1)=gds_element('boundary','xy',C2,'layer',1); % layer是图层
glib=gds_library('Circle_BLOCKS','uunit',1e-9,'dbunit',1e-12,gs); % 这里的默认单位为1e-9,也就是nm, 1e-12为精度
write_gds_library(glib,'!PC_phase.gds'); % gds文件命名为PC_phase2.代码分析
使用Matlab生成GDS图纸的核心逻辑是确定并存储每个单元结构的坐标。
这里所用的案例是1000*1000的圆形阵列,之所以用代码产生,是因为这个阵列圆的半径是不同的,并且规律很复杂。首先导入这个阵列的半径参数,并给待生成的GDS层命名。
以图纸的正中心为二维坐标系的零点,确定图纸的起点在左上角。坐标为(-x_length/2,y_length/2)。具体数值=均匀排布的间距(p)*采样阵列数(Nx or Ny)/2,不过在这之前需要判断阵列为奇数or偶数。
从循环中坐标的变换可以看出,这里的扫描是按列扫行,再变列。
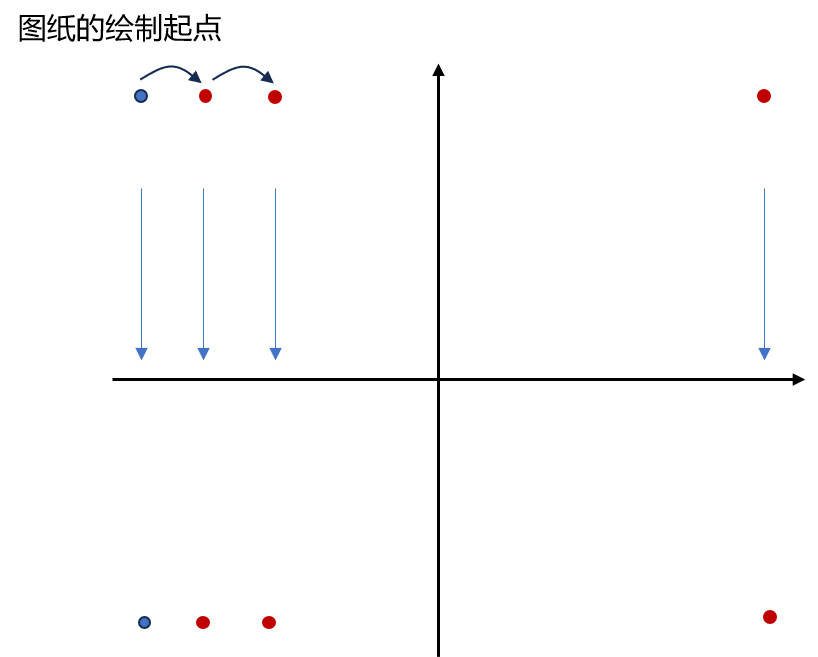
在确定了结构的中心位置之后,需要进一步确定边角的顶点坐标。从而让版图软件直接根据我们提供的坐标来连线绘图。对于矩形结构,除了中心坐标外还需要四个顶点坐标;而对于我们这里的圆结构,则需要对圆弧进行分段,为了尽可能逼近圆,这里以1°为一个间隔,将圆周量化为360个顶点。
从单个圆的局部坐标系来看,圆周上的顶点坐标可以简单由在一维轴上的投影得到。不过注意这里是相对坐标,顶点的绝对坐标还需加上圆心坐标,即(x + Δx, y+ Δy).
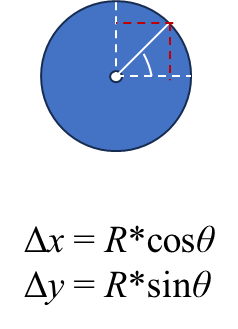
循环中的每个圆,先取得半径数值,再计算圆周上361个顶点坐标,最后与圆心坐标一起储存在元胞的对应位置中。
(PS:这里的单位为nm)
总结
以上就是利用matlab绘制GDS图纸的流程和基本逻辑,其他类型的图纸也可以通过增加或减少循环,或更改坐标标定规则来实现。