序列建模是深度学习的核心领域之一，旨在处理具有时序依赖关系的序列数据。从CNN到最新的Mamba模型，序列建模技术经历了革命性的演进，不断突破计算效率和建模能力的边界。
1 CNN
卷积神经网络（CNN）起初为图像而设计，但其通过一维卷积操作，同样能有效处理时间序列数据。CNN使用卷积核在输入序列上滑动，通过局部连接和权重共享提取局部特征。为了处理序列中的长程依赖，通常需要堆叠多层卷积网络，或采用扩张卷积等技巧来有目的地扩大模型的感受野。一个重要的演进是时序卷积网络，它通过因果卷积确保预测只依赖过去、扩张卷积扩大感受野，并结合残差连接，成为专门为序列任务设计的强大架构。
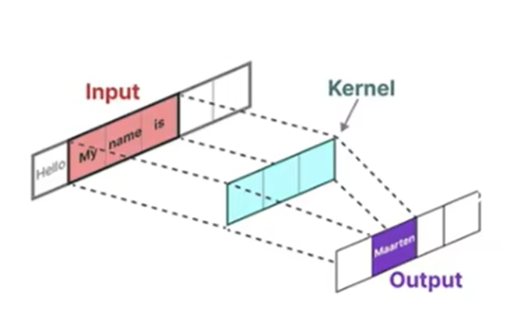
CNN的主要优势在于其高度的并行化能力，所有时间步的卷积计算可以同时进行，并且较短的路径使得梯度传播相对稳定，缓解了训练难题。然而，它存在两大根本局限：一是其结构本身更侧重捕捉局部特征，容易忽略全局特征，因为卷积核主要聚焦当前元素的邻近元素，无法让当前元素直接关注长程元素；二是它缺乏推理层面的优化，固定的卷积核限制了推理速度，相比RNN等结构，由于需要额外的乘加计算多个元素，其推理速度相对较慢。
2 RNN
循环神经网络（Recurrent Neural Network，RNN）是一种专门为序列数据设计的神经网络，结构图如下图所示：
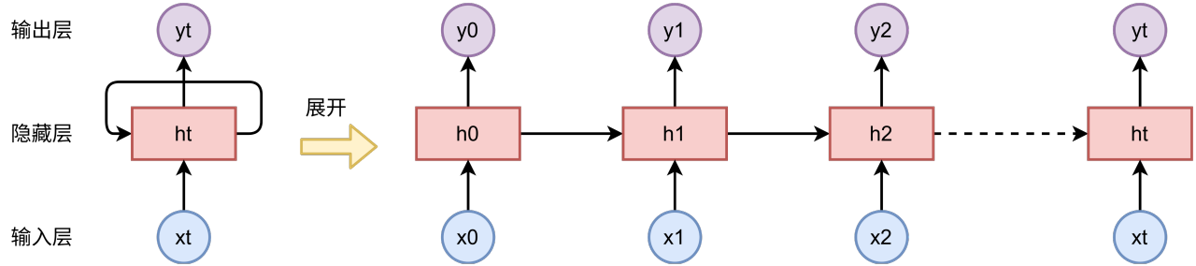
它的核心思想是通过引入循环连接和隐藏，实现对历史信息的记忆。相比于前馈神经网络的对每个输入独立处理，它在每一个时间步都通过接收当前输入和上一时刻的隐藏状态来更新当前时间步的隐藏状态，并传递给下一时刻，进而捕捉序列中的时序依赖关系，表达式如下：
在训练时，对于每个时间步，都需要接收当前时间步的输入和上一时刻的隐藏状态作为输入。这种链式的依赖关系，导致所有时间步的计算必须按顺序执行，无法像CNN那样将多个输入样本或时间步的计算分配到不同计算单元实现并行处理。在推理阶段，只需要通过接收当前时刻的隐藏状态即可得到输出，速度很快，近乎线性。但由于反向传播中的梯度消失和梯度爆炸问题，难以捕捉长期依赖。
3 Transformer
Transformer 的核心架构以自注意力机制为核心，彻底摆脱了循环神经网络的串行依赖，实现了序列数据的并行化处理。其整体结构如下图所示，由编码器（Encoder）和解码器（Decoder）两部分组成。
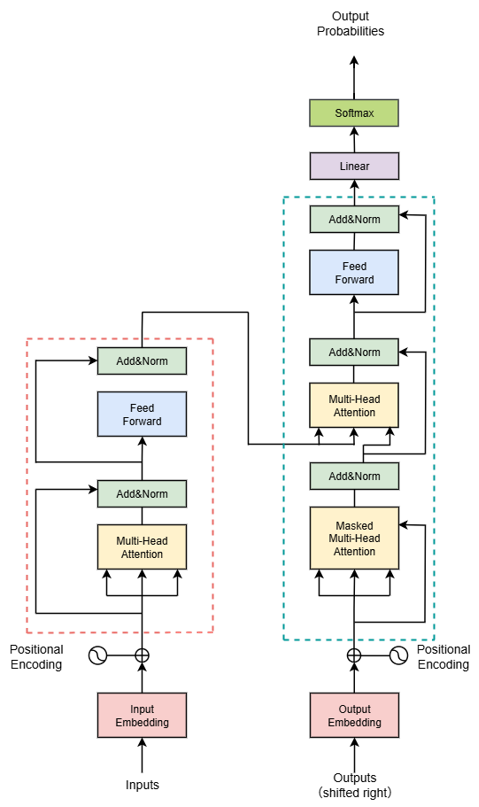
编码器 - 解码器架构包含 "编码器 + 解码器" 两个模块，编码器负责完整理解输入文本（比如翻译任务里的源语言），再将特征传递给解码器生成输出（目标语言），适配 "输入-输出" 类任务（如翻译、摘要）。
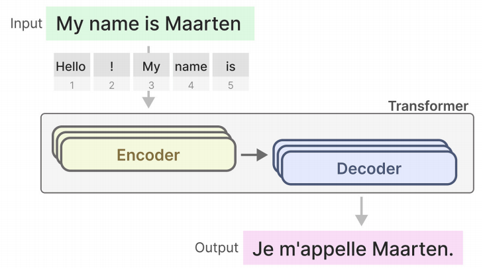
而单解码器架构是大语言模型（LLM）常用的架构形式，它仅保留解码器模块，输入文本直接进入解码器，通过自回归的因果注意力机制逐步生成后续内容，更专注于文本生成类任务（如聊天、创作）。
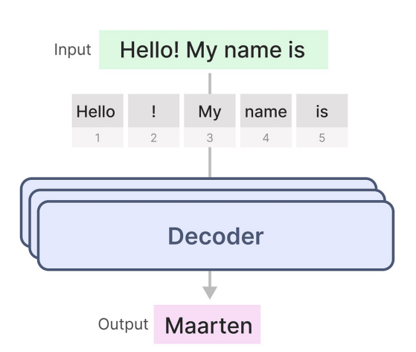
Transformer的解码器由N个结构相同的解码器层堆叠构成，其核心功能是基于编码器输出的全局上下文信息，生成符合任务要求的目标序列。每个解码器层包含三个关键子层，且每个子层都配备残差连接和层归一化，以保障信息流畅传递并稳定训练过程。
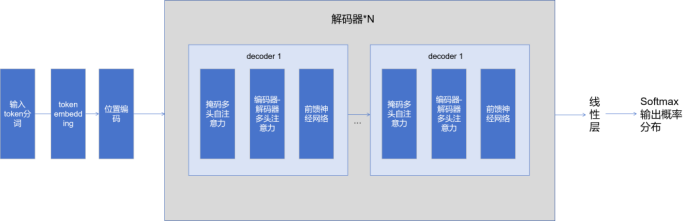
其中掩码多头自注意力机制的作用示意如下：
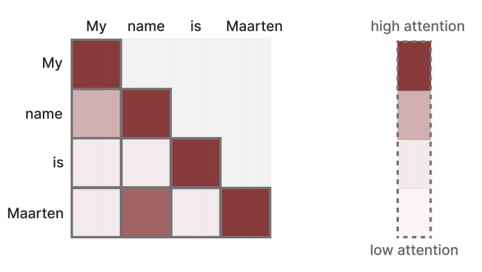
对于该句子中的4个Token，模型会同时将它们转化为 Query、Key、Value 矩阵，然后一次性计算所有Token之间的注意力分数。
掩码多头自注意力通过矩阵运算，一次性计算 "所有词对的注意力权重"。对一个长度为L的序列，注意力分数是一个L×L的矩阵，这个矩阵可以通过矩阵乘法一步算出，无需逐词处理。
在推理阶段，在生成每一个新token时，模型需要基于已生成的整个序列（长度为L）来计算注意力矩阵，其核心公式为：
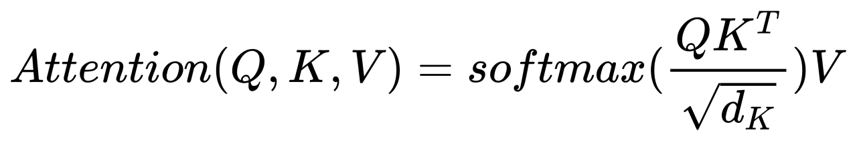
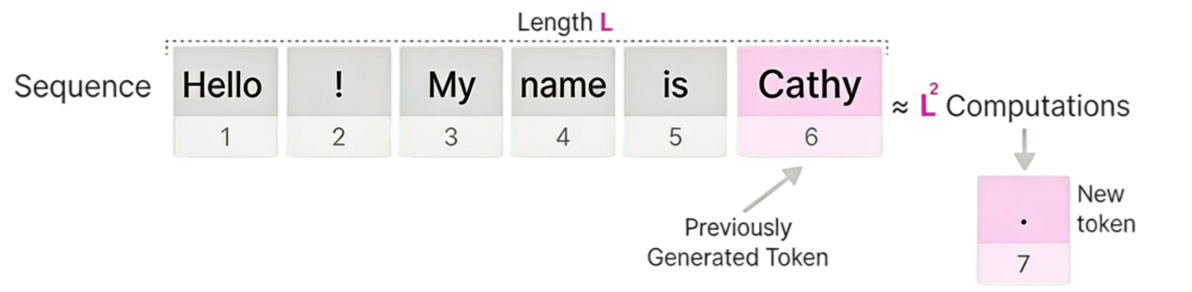
由于每次生成都需要对整个历史序列进行注意力计算，因此生成一个长度为L的序列所需的计算量大约与L²成正比，这导致了当序列变长时，推理成本会显著增加，成为Transformer模型在处理长序列时的一个关键瓶颈。
4 状态空间模型（State Space Model,SSM）
4.1 状态空间
状态空间是描述一个系统所需的最少状态数量，下图的迷宫即为一个动态系统，状态空间则是这个系统中所有可能状态的集合------每个状态由当前位置坐标(xi,yj)、可能的下一位置(xi',yj')可执行的动作（上下左右移动）、以及到达目标的距离等信息组成。
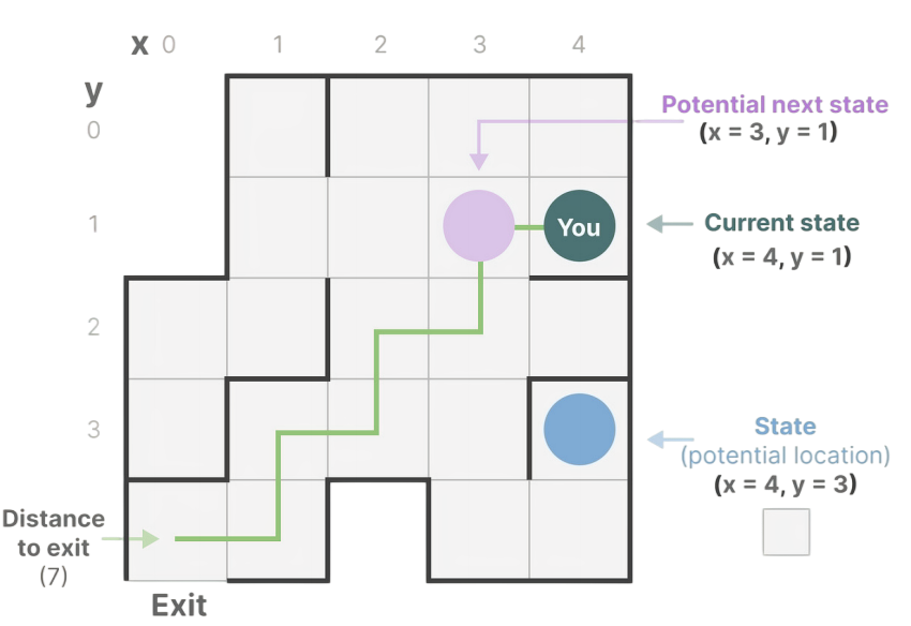
4.2 SSM的定义
SSM是一种用于描述系统状态，并能根据特定输入预测其下一状态的模型。考虑到输入一般都是连续的，它的一般表示是连续化形式，如下图所示：
其中，h(t)是上一时刻的隐藏状态，h'(t)是h(t)随时间的变化率，x(t)是当前时刻的输入，y(t)是最终输出。A是状态转移矩阵，作用是描述当前隐藏状态如何随时间演化。B是输入矩阵，C是输出矩阵，D是直接传递矩阵。
该图可以表示成下面的形式：
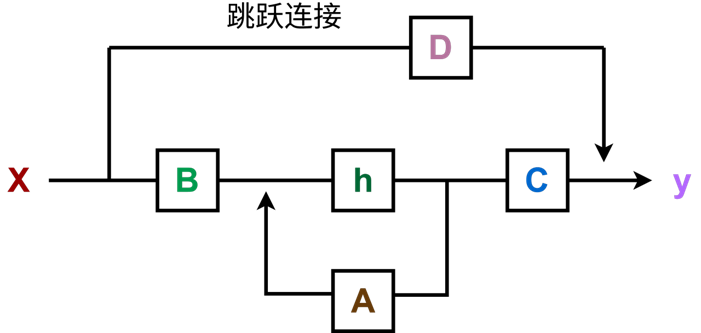
首先，输入信号x会先和输入矩阵B相乘，得到的向量会直接作用于系统的隐藏状态h------这一步的作用，是把输入信号的信息'注入'到系统的核心状态里。而隐藏状态h本身是一个承载了系统记忆的向量，它会和状态转移矩阵A相乘，这个过程描述了状态如何随时间动态更新，相当于系统在基于历史信息演化。
当状态更新完成后，输出矩阵C会把当前的隐藏状态映射到输出空间，让状态里的信息转化为输出信号；同时，输入信号x还会通过直接传递矩阵D直接作用于输出，也即跳跃连接，它能让输入的即时信息快速传递到输出端，避免信息在长流程中损耗。
最后，经过状态映射和跳跃连接的信号整合，系统就会输出最终的结果y。
4.3 离散化
自然语言处理中的任务大多数需要将序列进行分词成token进行处理，每一个token对应一个时间步。模型的输入本质上是离散时间步上的有限符号的集合，而不是连续的信号。因此，为了将状态空间模型应用于这些领域，必须将连续的微分方程转换为离散的差分方程，这个过程称为离散化。
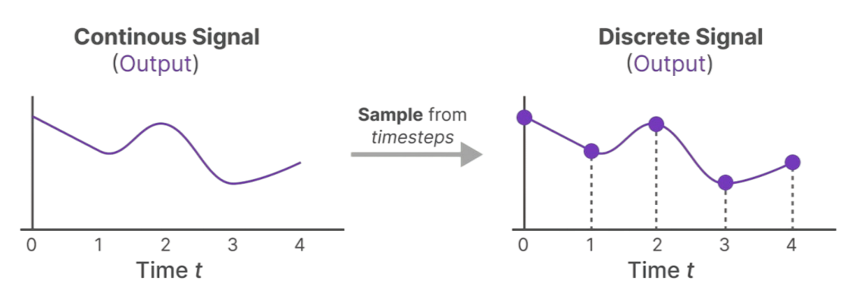
离散化常采用零阶保持技术。其具体做法是：在接收到离散信号的某个采样值后，立即更新输出信号为该值，并且在到达下一个采样时刻之前，始终将此值保持不变，形成一个"阶梯"状的波形。相邻阶梯之间的时间间隔，就是可学习的步长Δ。这个过程是为了给后续的连续系统提供一个可处理的、分段恒定的输入。
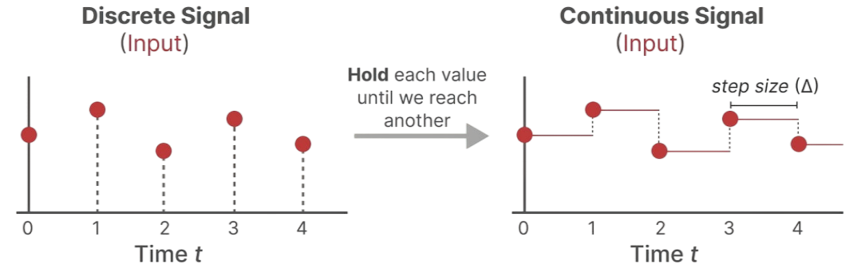
在输出阶段，我们需要从一个连续的系统输出信号中，通过采样得到我们最终需要的离散的输出信号。其具体做法是：在模型处理完连续的输入信号后，会产生一个连续的响应曲线。为了能在数字系统中使用这个结果，我们仅在特定的、与输入对齐的时间步长处（如图中t=0, 1, 2, 3, 4的时刻）对这条连续的输出曲线进行测量，提取其瞬间的值。这些被提取出来的离散点，就构成了模型的离散输出序列，完成了从连续域到数字域的转换。
在SSM中，我们对A和B进行采样，得到离散的两个矩阵：
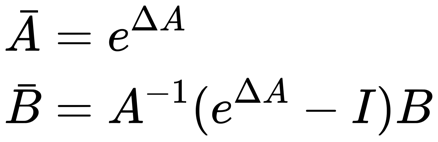
最终的表达式修改为：
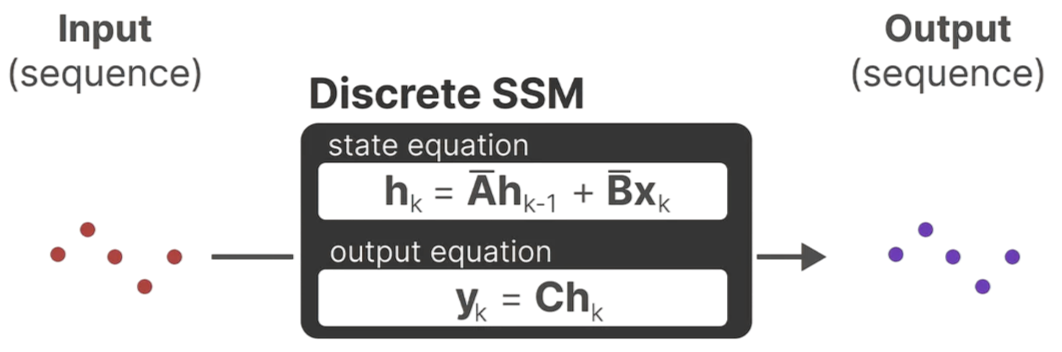
5 结构化状态空间模型（Structured State Space Model,S4）
在SSM中，状态维度为N，时间步维度为L。隐藏状态向量的大小为N*1，状态矩阵A的大小为N*N，计算复杂度为O(N²L)；模型需要存储每个时间步的状态向量，每个状态向量大小为N，因此总内存占用为O(NL)。
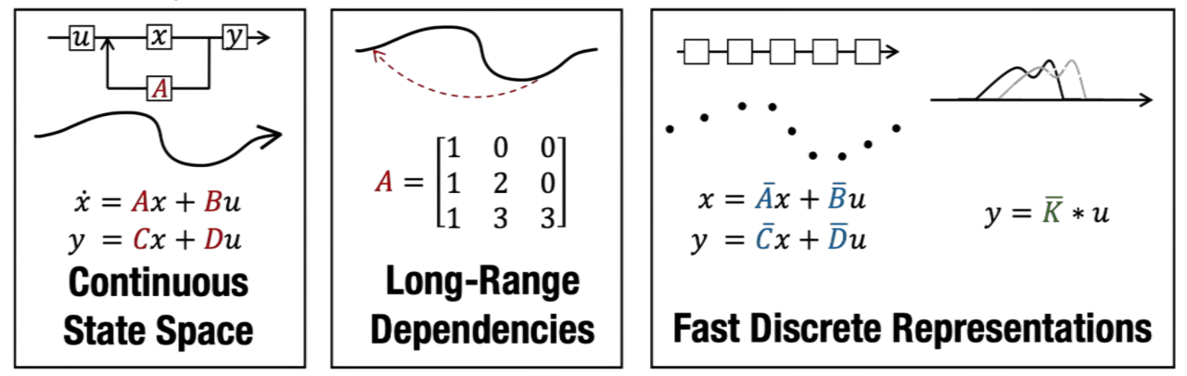
S4引入了一种新型参数化方法，能够高效地在连续状态空间表示、长程依赖表示、快速离散表示这三种表征之间切换，在多种任务的训练和推理过程中均保持高效，并在长序列处理方面表现出色。
5.1 循环结构表示
下图直观地展示了S4模型的循环（RNN）表示模式，这是其在推理阶段实现线性时间复杂度与低内存消耗的关键。
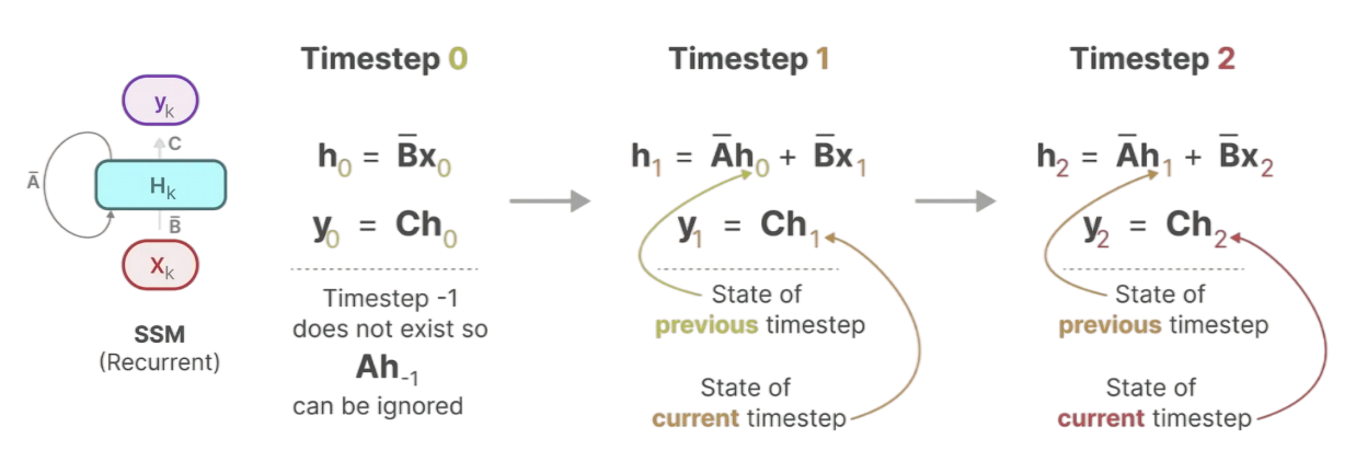
每个新状态都仅依赖于前一状态和当前输入，而无需回顾整个历史。这种结构使得模型在推理时，只需在内存中维护一个固定大小的状态向量，即可持续处理任意长度的序列，从而实现了与序列长度无关的常数级内存增长和线性时间复杂度的序列生成，这正是S4相比Transformer等模型在处理长序列时的核心效率优势所在。
5.1 卷积结构表示
输入序列u通过与一个结构化的一维卷积核进行卷积操作，将递归运算转化为卷积操作，最终得到输出序列y。
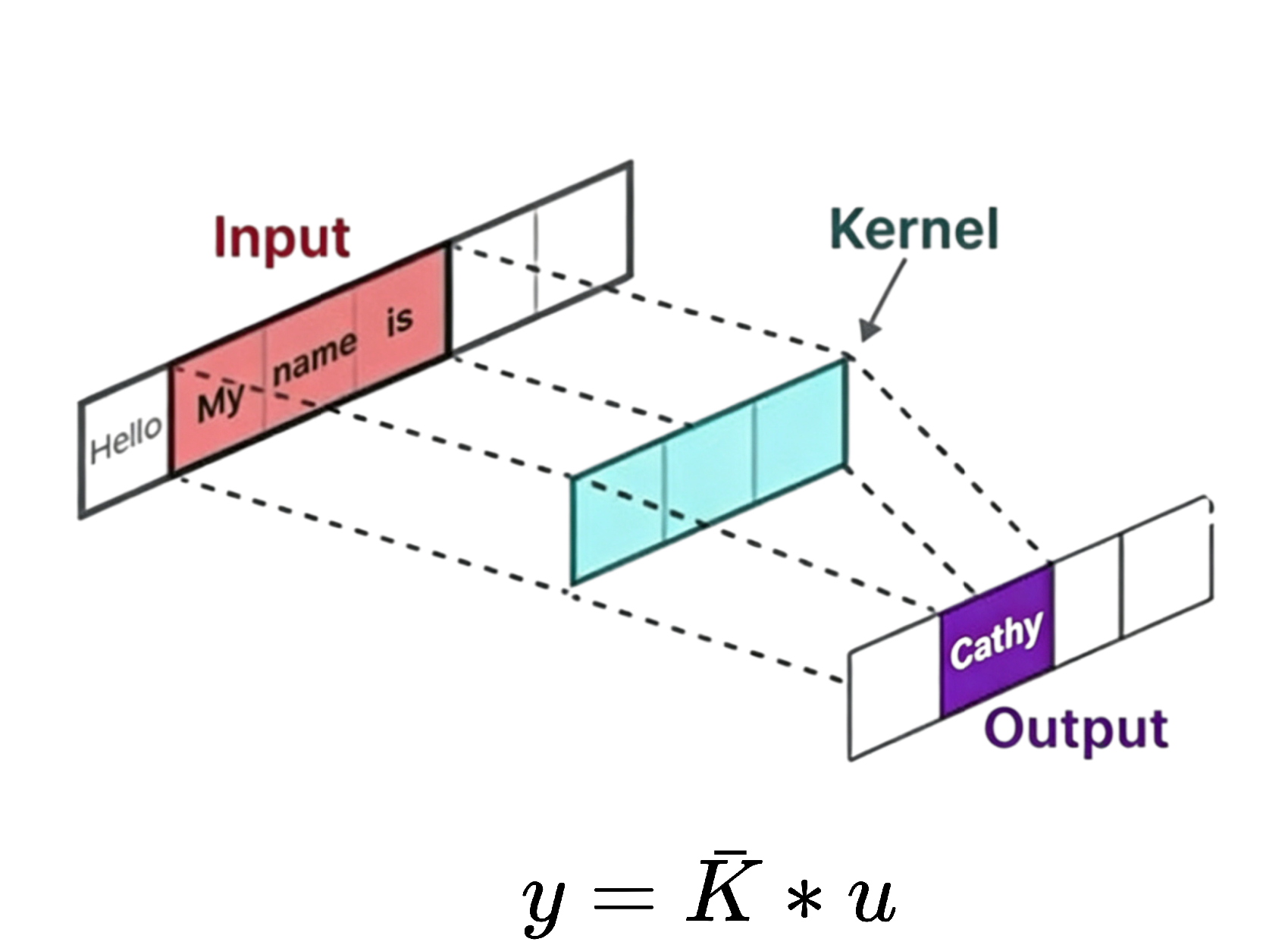
相比于传统卷积的局部运算，S4采用了全局卷积，每个输出位置都依赖于整个输入序列。在下图的文本生成任务中，输入是"My name is"，长度为3，这三个单词分别可以表示为x0、x1、x2，卷积核的大小也为3。
在序列之前使用Padding在输入序列前填充0，将S4特有的、单向的因果卷积，在序列起始位置的计算过程，直观地类比成传统CNN中卷积核滑动的形式，使三元素的卷积核能与一个完整的窗口对齐，从而说明在计算第一个输出
时，虽然卷积核有三个系数，但实际起作用的只有对应
的
这一个。
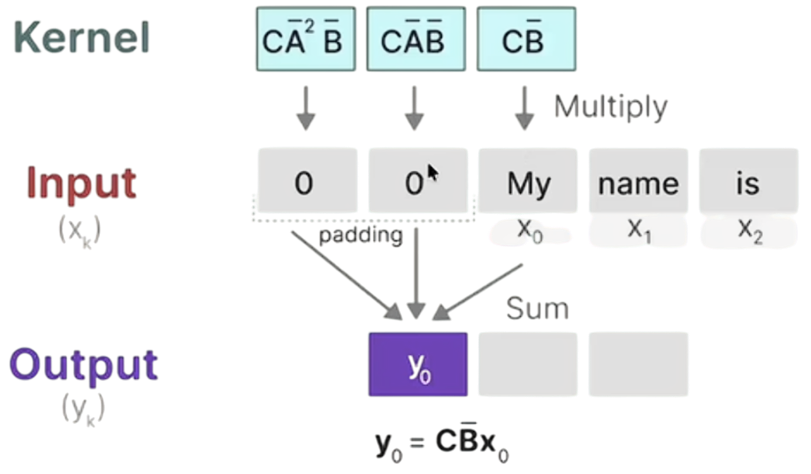
每个位置的输出计算如下：
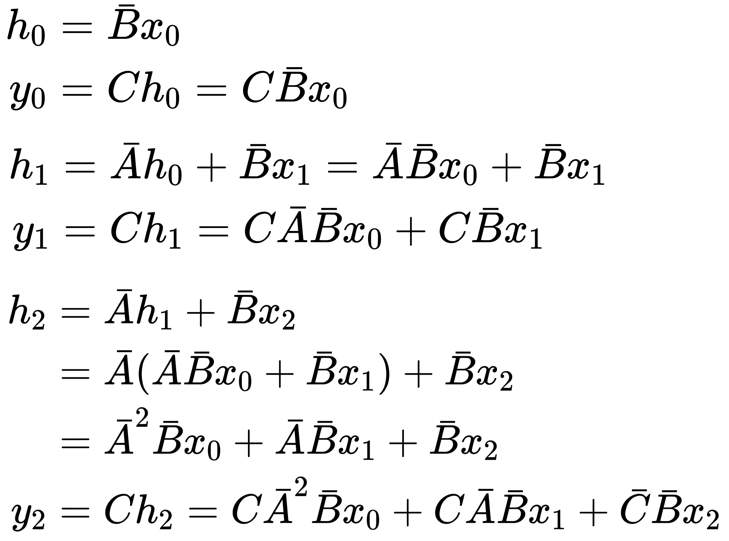
可以写成下面的卷积表示形式：
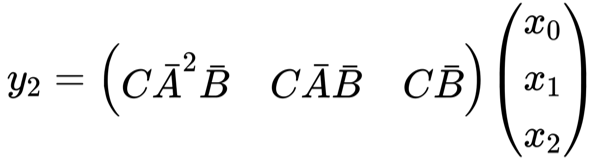
通过寻找规律，我们可以得到卷积核的一般表达式：
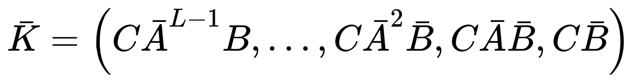
5.3 两种表示的优缺点
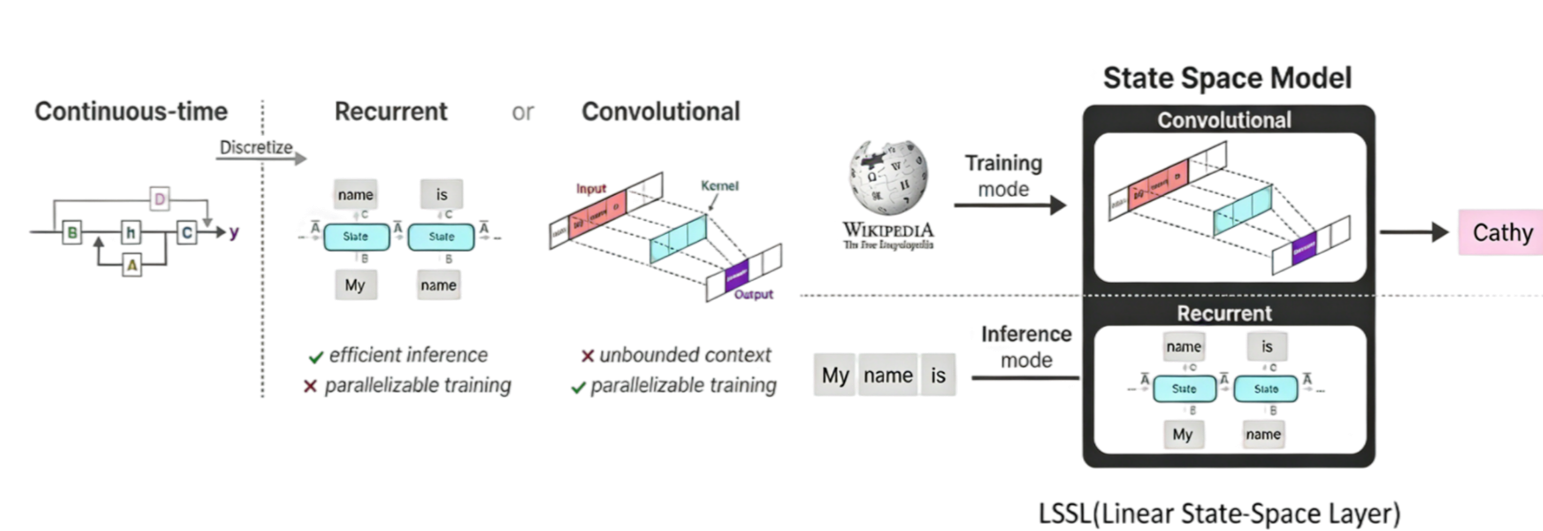
循环结构表示参考RNN的形式，能够实现快速推理，但是由于时间步之间存在依赖关系，无法进行并行训练。卷积结构表示可以实现并行训练，但是依赖固定长度的卷积核，只能覆盖 "卷积核尺寸以内" 的有限上下文；当输入序列的上下文长度超过卷积核的固定长度时，模型无法捕捉超出部分的信息。
线性状态空间层则结合了两者优势：训练阶段用卷积形式，推理阶段切换为递归形式，以此兼顾训练效率与推理时的长上下文需求。
5.4 Hippo矩阵
5.4.1 核心思想
在状态更新公式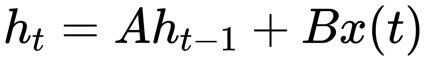
中，矩阵A负责从历史状态中提取和传递信息，其初始化方式直接决定了模型捕捉长期依赖的能力。传统SSM随机初始化A效果有限，而S4模型采用了HiPPO矩阵初始化A，其结构能更科学地压缩历史信息：
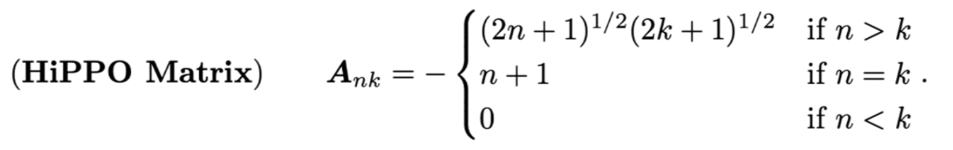
这个矩阵A定义为一个下三角矩阵，其元素的值由n（当前维度/时间尺度）和k（历史维度/时间尺度）的大小关系决定。当n>k时，元素为两个平方根的乘积，这建立了一种跨时间尺度的耦合，让模型能将更远的历史信息"投影"并整合到当前状态中；当n=k时，元素值随维度线性增长，这赋予了近期信息更强的权重；而当n<k时元素为0，确保了模型严格遵循因果性（当前状态只依赖过去，不依赖未来）。
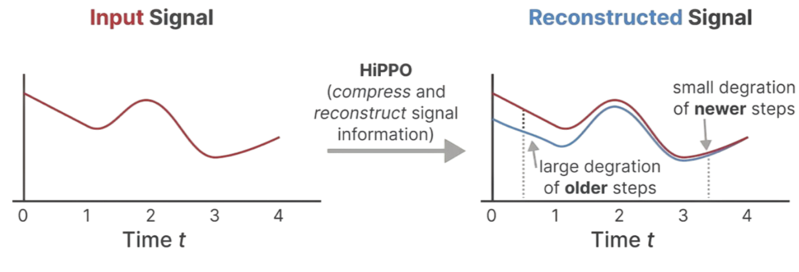
下面的波形图体现了Hippo矩阵的作用------重建信号能有效保留近期输入，同时对更早期的信号进行合理的"遗忘"。
5.4.2 矩阵分解
在卷积形态中，需要预计算一个长度为的卷积核
，这涉及到计算矩阵
的幂次（即
的效果）。如果直接使用原始的HiPPO矩阵
进行计算，其复杂度高达 O(N²L)（其中
是状态维度，
是序列长度），这在处理长序列时是无法承受的。
解决方法是将原始的Hippo矩阵转换为正规矩阵+低秩矩阵的形式：
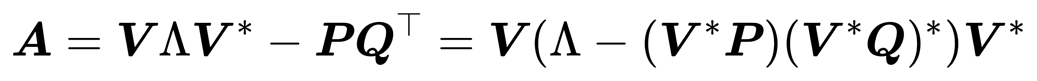
其中：
：一个正规矩阵（由其特征向量
和对角特征值矩阵
构成）。正规矩阵的良好性质是，它的任意幂次
可以简单地转化为
，计算从复杂的矩阵乘法降为简单的对角矩阵幂运算，效率极高；
：一个低秩矩阵，其中
P和Q是两个低秩矩阵。显著降低了计算复杂度和参数存储空间。
在状态空间模型的RNN形式中，状态更新公式的计算复杂度是O(N)，其中N是状态维度。这个复杂度只与状态向量的维度有关，而与矩阵A的具体结构（是否分解、是否低秩）完全无关。
矩阵分解的真正作用体现在训练阶段的卷积形式计算中。在卷积形式下，需要计算矩阵A的幂次，这会导致O(N²L)的复杂度。通过将A分解为正规矩阵和低秩矩阵的和，可以利用正规矩阵的对角化特性和Woodbury引理，将复杂度降低到Õ(N + L)（Õ表示忽略对数因子），实现高效的并行训练。
5.5 总结
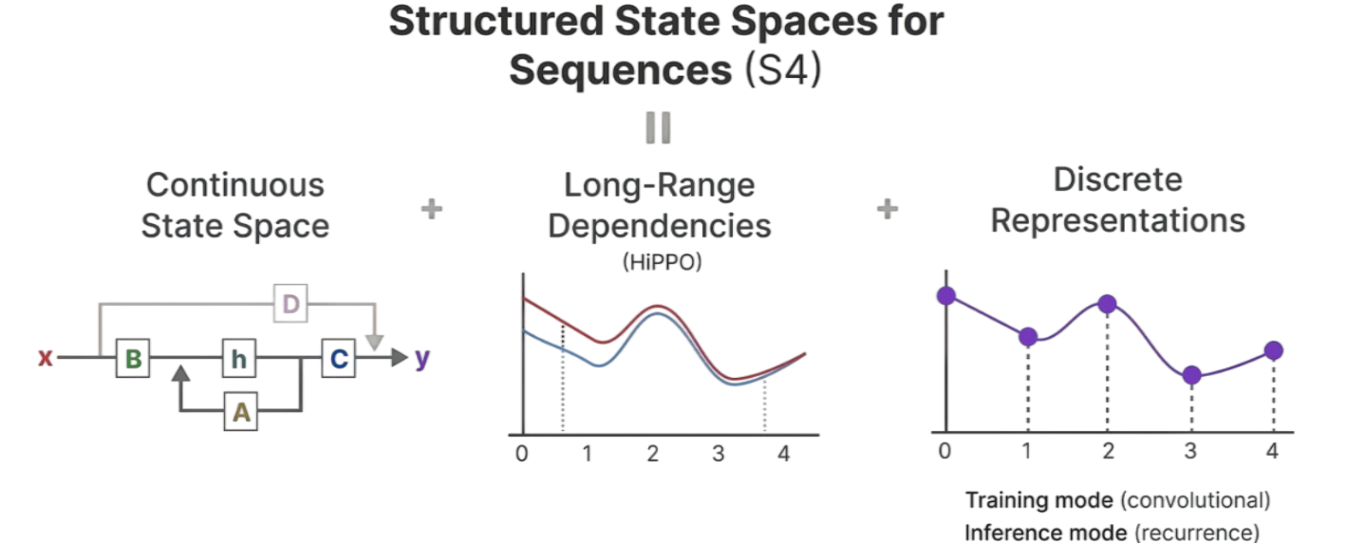
S4的核心构成可拆解为连续状态空间、长距离依赖处理和离散表示3个关键模块。连续状态空间呈现了 S4 的基础状态更新框架，这是 S4 实现序列建模的底层结构；长距离依赖处理（Long-Range Dependencies）借助 Hippo 矩阵实现；离散表示同时支持 "卷积形式" 和 "递归形式" 这两种不同的离散计算范式，适配了 S4 "训练" 和 "推理" 的不同需求。
5.6 S4的缺陷
S4具有几个核心缺陷：首先，它基于线性时不变系统构建，该系统的动态特性不会随输入或时间变化，灵活性较差；其次，模型缺乏输入选择性，无法根据输入内容自适应地决定重点关注哪些信息；再次，它在训练与推理的表示上存在矛盾，它们的表示逻辑存在差异，可能导致训练效果与推理效果不一致。
以下面的任务为例，模型需要从输入中有选择地提取所有的名词，理想情况下是输出Cats和yarn，但是S4可能做不到。
6 Mamba
Mamba在S4的基础上主要做了两点改进：选择性机制（Selective）和并行扫描算法（Scan）。因此，它的核心模块也被称为S6。
它的架构图如下图所示，结合了H3模块和MLP模块进行了改进，其核心是一个Mamba Block。
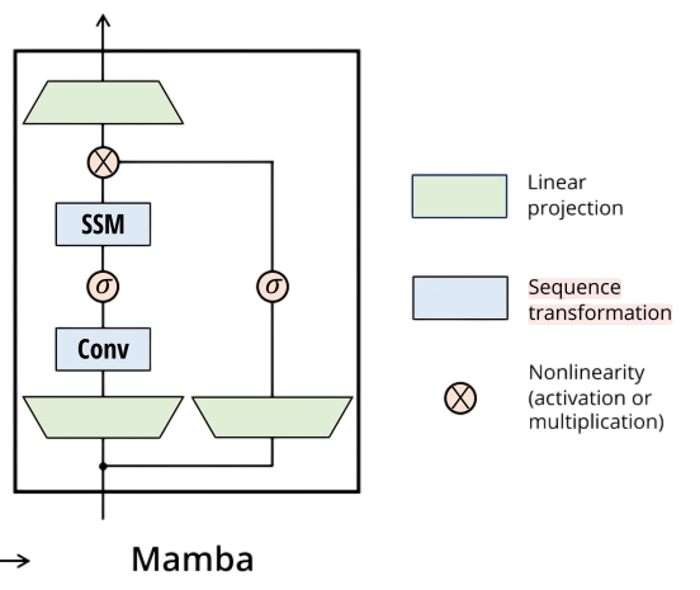
下面是Mamba Block的内部结构。
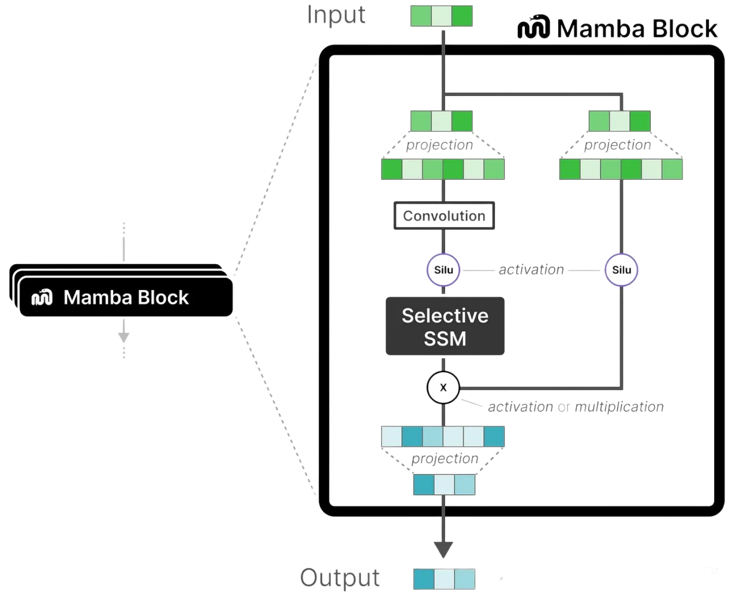
其工作原理是一个循环处理过程：输入首先进行输入投影，将输入序列映射到适合选择性SSM模型处理的维度。接着数据分为两路，一路通过一个卷积模块来捕获局部特征，之后通过SiLU激活函数引入非线性。另一路数据经过另一个线性层，再经过Sigmoid函数，生成门控信号g。最后，SSM路径的输出与门控信号g进行逐元素相乘，结果再经过输出投影，产生Mamba Block的最终输出。
6.1 选择性机制
选择性机制让参数矩阵B、C能够根据当前的输入进行动态调整，使得模型能够动态地选择性地传播或遗忘信息，从而解决了S4缺乏输入选择性的固有问题。S4和S6使用的两种算法的对比如下：
SSM (S4) 算法算法是基础的结构化状态空间模型。它接收一个形状为 (B, L, D) 的输入序列x，并输出一个相同形状的序列y。模型的核心是可学习的参数：矩阵A（N×N状态转移矩阵）、B 和 C，它们的形状均为 (D, N)。此外，还有一个通过函数生成的参数Δ，它控制着时间步长的离散化。
该模型的关键特性是时间不变性:所有参数（A, B, C, Δ）一旦被学习或初始化，就在整个序列的所有时间步上保持固定，不随输入内容的变化而改变。因此，在第五步进行离散化后，得到的离散矩阵和
也是固定的。这种时间不变性带来了一个重要的计算优势：第六步中的 SSM 计算，既可以通过对隐状态进行线性递推来完成，也可以等效地转换为一个全局卷积操作，这为训练和推理提供了灵活性。
SSM + Selection (S6) 算法的输入和输出形式与 S4 相同，但内部机制发生了根本性变化。它引入了"选择"机制，使模型的关键参数能够依赖于输入。
具体来说，模型中只有A 矩阵保持为全局可学习参数。而其他参数则动态生成：B 和 C 矩阵分别由输入x通过投影函数 和
实时生成，因此它们在每个批次、每个时间步都可以不同。时间步长参数Δ 则由一个基础参数加上输入x的函数
共同决定。这使得模型从"时间不变"转变为时间变化。由于参数在每个时间步都不同，第五步离散化后得到的
和
也变为四维张量 (B, L, D, N)。
这种时间变化特性带来了计算方式的改变。由于参数不再固定，无法推导出一个全局的、固定的卷积核，因此第六步中的SSM计算只能使用递推（Scan）方式逐时间步进行。这使得模型能够根据当前输入内容选择性地传递或遗忘信息，显著增强了其上下文感知和建模能力，但计算形式受到了限制。
6.2 并行扫描
并行扫描算法的引入，是为了解决Mamba模型在训练阶段面临的核心效率难题。如前所述，选择性机制使模型参数（B, C, Δ）变为输入依赖，这导致离散化后的状态矩阵Ā和输入矩阵B̄在每个时间步都不同，模型因此成为一个时间变化系统。时间变化性使得S4中那种将整个递推过程转换为一个固定全局卷积核的高效训练方法不再适用，因为每一步的操作都独一无二，无法预先计算一个统一的卷积核。
如果退回到像传统RNN那样，在训练时也严格按时间顺序一步一步进行递推计算，虽然可行，但会丧失宝贵的并行性，导致训练速度极其缓慢，无法利用现代GPU的大规模并行计算能力。这构成了一个矛盾：选择性机制带来了强大的建模能力，却可能牺牲训练效率。
并行扫描算法正是破解这一矛盾的关键。它本质上是一种允许对关联性操作进行并行化计算的算法。所谓关联性操作，指的是类似加法、乘法那样满足结合律的操作。一个简单的例子是计算一个序列的前缀和：[x1, x2, x3, ...] 的前缀和序列是 [x1, x1+x2, x1+x2+x3, ...]。虽然这个计算看起来是顺序依赖的（每个和都依赖于前一个结果），但通过巧妙的树状合并策略，可以在对数时间内并行计算出所有前缀和。
Mamba中的状态更新公式 正是一种广义的、系数可变的前缀计算形式。这里，"操作"不再是简单的加法，而是"乘以
然后加上
"这个复合操作。虽然每个时间步的
和
不同，但只要操作形式固定，并行扫描算法就能将这种线性递推计算重新组织。
具体来说，算法会将整个序列的递推计算构造成一棵计算树。在树的底层，先并行计算相邻时间步的局部组合结果；然后逐层向上，将这些局部结果两两合并，最终在log(L)层合并后，得到所有时间步的隐状态。这个过程允许GPU将大量细粒度的矩阵-向量乘法与加法操作同时进行，从而在训练时实现了高效的并行化，其耗时与序列长度L近似呈线性关系。
因此，并行扫描让Mamba鱼与熊掌兼得：在训练时，它通过并行的树状扫描算法，保持了与Transformer相当的序列并行训练效率；在推理时，它则切换回经典的、内存效率极高的顺序递推模式（RNN模式），生成每个新token仅需常数时间。这使得Mamba既能拥有基于内容的选择性感知能力，又能在实际应用中实现高效的训练和快速的推理，从而在长序列建模任务中展现出卓越的综合性能。
7 总结
总体而言，Mamba通过选择性机制与并行扫描算法的结合，完成了对序列建模范式的一次重要演进。选择性机制赋予了模型动态的、输入依赖的上下文建模能力，使其能够像注意力机制一样进行内容感知，解决了S4模型僵化与缺乏选择性的核心缺陷；而并行扫描算法则提供了强大的计算引擎，破解了时间变化系统在训练时的并行化难题，保障了模型可被高效训练。这一组合使Mamba能够在语言、音频、基因组学等众多领域的长期依赖建模任务中取得突破性表现，成为连接经典递归模型与现代并行架构的一座高效桥梁。