算法学习入门---二叉树

目录

1.二叉树的性质

2.二叉树的存储

顺序存储：

链式存储：

3.深度优先遍历（dfs）

4.宽度优先遍历（bfs）

5.二叉树算法题

洛谷---新二叉树

洛谷---二叉树的遍历

洛谷---【深基16.例3】二叉树深度

[洛谷--- [NOIP 2001 普及组] 求先序排列](#洛谷--- [NOIP 2001 普及组] 求先序排列)

[洛谷--- [USACO3.4] 美国血统 American Heritage](#洛谷--- [USACO3.4] 美国血统 American Heritage)

[洛谷--- [JLOI2009] 二叉树问题](#洛谷--- [JLOI2009] 二叉树问题)

---

1.二叉树的性质

二叉树必须是一棵有序树，也必须是一棵有根树，同时每个节点有且仅有左右两个孩子结点

1. 高度为h的满二叉树，结点个数为2^h-1（等比数列求和）
2. 结点为n的满二叉树，高度为log2^n+1
3. 按照层序遍历将二叉树从根节点开始从1编号，则有以下三条性质：

• 结点 i 左孩子的编号为 2*i
• 结点 i 右孩子的编号为 2*i + 1
• 结点 i 双亲的编号为 i/2

2.二叉树的存储

二叉树也是树，可以用 vector数组 或 链式前向星 来存储，仅需在存储的过程中标记谁是左孩子谁是右孩子即可。

• 比如vector数组，可以先尾插左孩子，再尾插右孩子
• 链式前向星存储时，可以先头插左孩子再头插右孩子，但遍历孩子的时候会先遍历到右孩子

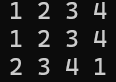
顺序存储：

不用vector数组来存储，完全二叉树的存储还可以通过一个极大的数组，然后按照层序遍历将二叉树从根节点开始从1编号，根据编号依次将结点放在数组对于的位置上。（如上图所示）

通过这种办法，就可以有效地使用到完全二叉树的各种性质，简化了我们的操作

---

如果不是一棵满二叉树或完全二叉树，也可以通过完全二叉树的思想来存储。将空出来的位置，用null（无效字符）来代替，通过这样的操作把一棵树补成一棵完全二叉树，这样就即能简化存储又能使用完全二叉树的各种性质

但这种办法因为需要补足完全二叉树，所以空间利用率特别低。也因此，顺序存储只适用于满二叉树或者完全二叉树或接近满的二叉树。

链式存储：

因为二叉树是一棵有序二叉树，所以可以直接用数组下标作为父节点，定义两个数组 l 和 r，分别表示为某一下标作为父节点的左孩子与右孩子，因为这样存储可以编号与元素一一对应，所以不需要e数组（元素数组）的辅助，同时也存储了结点与结点之间的关系（如果元素不是int型数据，可以再借助e数组的辅助，或者转换为可以一一对应的下标）

需要注意的是先输入的是左孩子结点，后输入的是右孩子结点，顺序不能颠倒

代码：

#include<iostream>
using namespace std;

const int N = 1e6+10;
int l[N],r[N];

int main()
{
	int n;cin>>n;//结点个数
	for(int i=1;i<=n;i++)
	{
		cin>>l[i]>>r[i];	
	} 
	return 0;
}

3.深度优先遍历（dfs）

二叉树的遍历分为了先序、中序、后序三种，实现方式与动态方式思想差不多。

因为是有根树，所以不需要bool数组的辅助了。

代码：

#include<iostream>
using namespace std;

const int N = 1e6+10;
int l[N],r[N];
void dfs1(int root)//先序
{
	cout<<root<<" ";
	if(l[root])dfs1(l[root]);
	if(r[root])dfs1(r[root]);
}
void dfs2(int root)//中序
{
	if(l[root])dfs2(l[root]);
	cout<<root<<" ";
	if(r[root])dfs2(r[root]);
}
void dfs3(int root)//后序
{
	if(l[root])dfs3(l[root]);
	if(r[root])dfs3(r[root]);
	cout<<root<<" ";
}

int main()
{
	int n;cin>>n;//结点个数
	for(int i=1;i<=n;i++)
	{
		cin>>l[i]>>r[i];	
	} 
	dfs1(1);
	cout<<endl;
	dfs2(1);
	cout<<endl;
	dfs3(1);
	cout<<endl;
	return 0;
}

4.宽度优先遍历（bfs）

层序遍历整个二叉树，方法和一般的树几乎一模一样。

代码：

#include<iostream>
#include<queue>
using namespace std;

const int N = 1e6+10;
int l[N],r[N];
void bfs()
{
	queue<int> q;
	q.push(1);
	while(q.size())
	{
		int val = q.front();q.pop();
		cout<<val<<" ";
		if(l[val])q.push(l[val]);
		if(r[val])q.push(r[val]);
	}
}

int main()
{
	int n;cin>>n;//结点个数
	for(int i=1;i<=n;i++)
	{
		cin>>l[i]>>r[i];	
	} 
	bfs();
	return 0;
}

5.二叉树算法题

洛谷---新二叉树

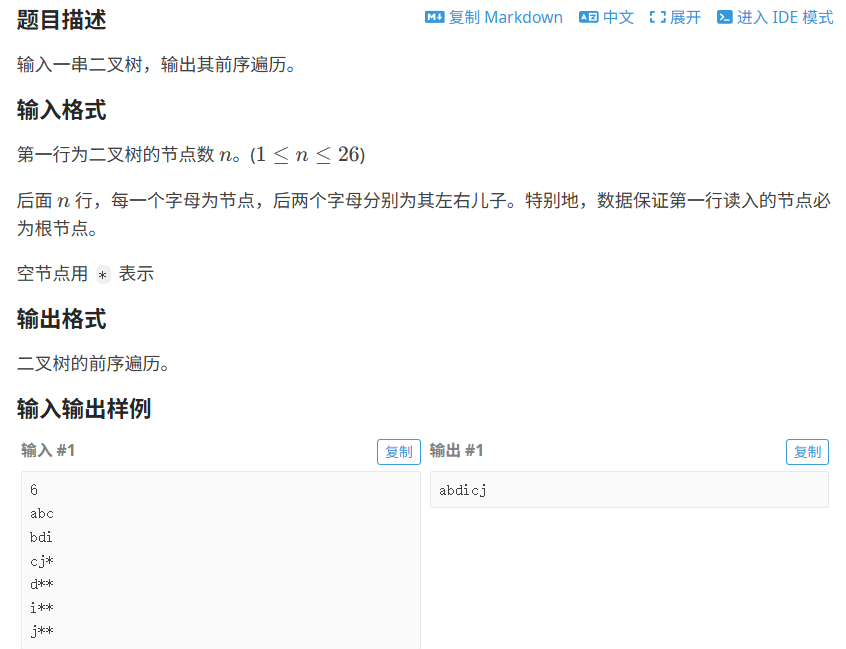
考察树的前序遍历

代码：

#include<iostream>
#include<string.h>
using namespace std;

const int N = 30;
int l[N],r[N];
void dfs(int root)
{
	char ch = root+'a';
	cout<<ch;
	if(l[root]!=-1)dfs(l[root]);
	if(r[root]!=-1)dfs(r[root]);
}

int main()
{
	memset(l, -1, sizeof(l));
	memset(r, -1, sizeof(r));
	int n;cin>>n;
	int flag = 1,st = -1;
	while(n--)
	{
		char root,left,right;cin>>root>>left>>right;
		if(left>='a'&&left<='z')l[root-'a']=left-'a';
		if(right>='a'&&right<='z')r[root-'a']=right-'a';
		if(flag)//第一次输入 
		{
			flag=0;
			st = root-'a';
		}
	}
	dfs(st);
	return 0;
}

代码易错点：如果要将数组中所有元素初始化为-1，则需要通过memset关键字

memset(l, -1, sizeof(l));

memset(r, -1, sizeof(r));

---

本题除了通过整型数组来ac，也可以直接通过char数组来解决，只不过需要开一个空间比较大的数组，这样数组下标就直接可以对应字母的acs码值，至少要开150个空间来存储

洛谷---二叉树的遍历

代码同上文中的深度优先遍历

洛谷---【深基16.例3】二叉树深度

代码1：

#include<iostream>
using namespace std;

const int N = 1e6+10;
int l[N],r[N];
int ret=0;
void dfs(int root,int h)//先序
{
	h++;
	if(h>ret)ret=h;
	if(l[root])dfs(l[root],h);
	if(r[root])dfs(r[root],h);
}

int main()
{
	int n;cin>>n;//结点个数
	for(int i=1;i<=n;i++)
	{
		cin>>l[i]>>r[i];	
	} 
	dfs(1,0);
	cout<<ret;
	return 0;
}

代码解释：通过先序遍历的方式来统计层数，不要用中序遍历或后序遍历，这样会导致最左边的叶节点 h=1，而根节点的 h = 整棵树的深度，比较难理解

把先序遍历中的打印结点操作换为统计当前结点为树的第几层即可，由于递归过程中是传值传参，所以子节点的h修改不会影响父节点的h

代码2：

#include<iostream>
using namespace std;

const int N = 1e6+10;
int l[N],r[N];
int dfs(int root)//先序
{
	if(!root)return 0;
	return max(dfs(l[root]),dfs(r[root]))+1;
}

int main()
{
	int n;cin>>n;//结点个数
	for(int i=1;i<=n;i++)
	{
		cin>>l[i]>>r[i];	
	} 
	cout<<dfs(1);
	return 0;
}

代码解释：

直接从叶节点往上一层一层返回深度，找到根节点的左右子树中深度更大的那个进行返回；遇到模拟的空结点直接返回0，表示开始统计当前子树的深度

洛谷--- [NOIP 2001 普及组] 求先序排列

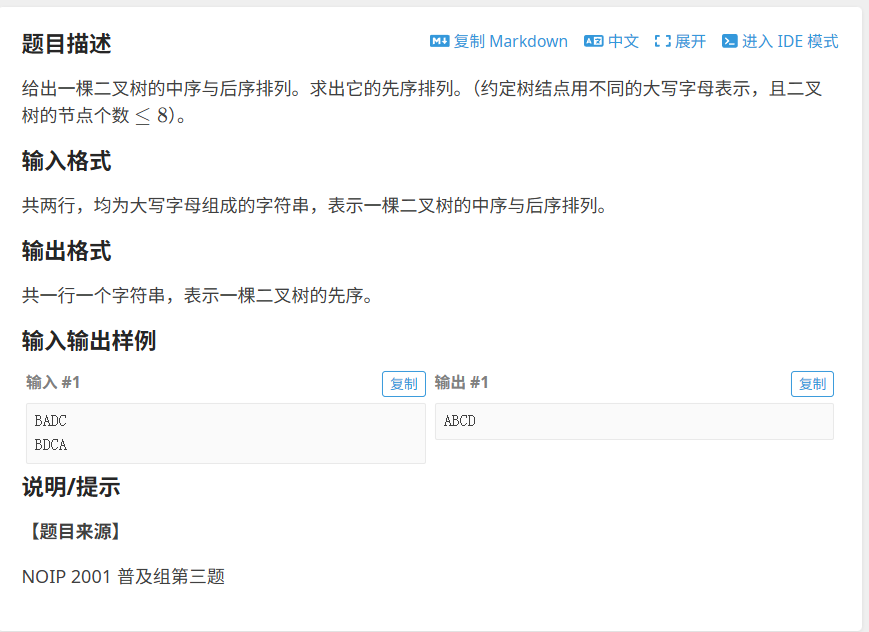
给出二叉树的中序、后序排列，求二叉树的先序排列

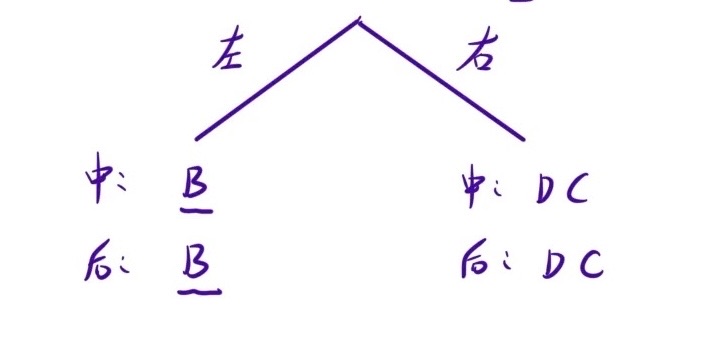
通过后序遍历的定义可以得知：后序遍历最后输入的一定是根节点

那么找到了根节点以后，中序遍历代表左根右，所以B是左子树、D和C是右子树

把这个思想推广到一般情况，即：

1. 先确定根节点（通过后序遍历）
2. 根据根节点，划分出左右子树（通过中序遍历）

如下图所示，在把一整棵树划分为左右两棵子树后右子树为DC，再把右子树看成一个完整的树，然后通过后序遍历确定根节点，根据根节点划分出左右子树即可

不断重复上述操作，每次都先输出根结点的值，然后划分完左右子树后，先对左子树进行重复

代码：

#include<iostream>
using namespace std;

string a,b; 

void dfs(int l1,int r1,int l2,int r2)//中序、后序的l、r坐标
{
	//递归出口（必须要有，要不然会一直dfs下去） 
	if(l1>r1) return;
	//找到根节点
	cout<<b[r2];
	char root = b[r2];	
	int cur = l1;//找到中序字符串中的根节点
	while(a[cur]!=root)cur++;
	
	//对左区间进行dfs
	dfs(l1,cur-1,l2,l2+cur-l1-1);
	//对右区间进行dfs 
	dfs(cur+1,r1,l2+cur-l1,r2-1);  
} 

int main()
{
	cin>>a>>b;
	dfs(0,a.size()-1,0,b.size()-1);
	return 0;
}

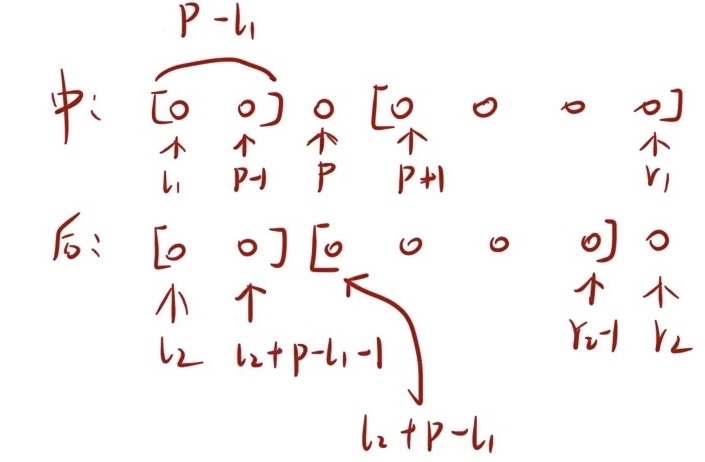
代码重点解释：

如上图1所示，我们可以用分治的思想来处理这个问题；即找到根节点以后，划分为左右两区间，然后对左右区间再进行操作

如上图2所示，中序遍历的字符串左右区间位置比较容易确定，左区间共有p-l1个元素，所以在后序遍历的字符串左区间中也只有p-l1个元素，但因为下标是从0开始的，所以后序遍历字符串左区间的终止位置为l2+p-l1-1，其右区间的终止位置需要是r2-1，把最后一个根节点去除

洛谷--- [USACO3.4] 美国血统 American Heritage

给出中序、前序遍历，求后序遍历

代码：

#include<iostream>
using namespace std;

string a,b; 


void dfs(int l1,int r1,int l2,int r2)//中序、前序的l、r坐标
{
	//递归出口（必须要有，要不然会一直dfs下去） 
	if(l1>r1) return;
	//找到根节点
	char root = b[l2];	
	int cur = l1;//找到中序字符串中的根节点
	while(a[cur]!=root)cur++;
	
	//对左区间进行dfs
	dfs(l1,cur-1,l2+1,l2+cur-l1);
	//对右区间进行dfs 
	dfs(cur+1,r1,l2+cur-l1+1,r2);  
	cout<<root;
} 

int main()
{
	cin>>a>>b;
	dfs(0,a.size()-1,0,b.size()-1);
	return 0;
}

代码易错点：l2是位于根节点的，所以左区间的截止位置与其距离正好为左区间元素个数

洛谷--- [JLOI2009] 二叉树问题

输入时，前一个输入为父节点后一个输入为子节点

距离为源节点到目标节点的祖先节点边数的2倍+祖先节点到目标结点边数

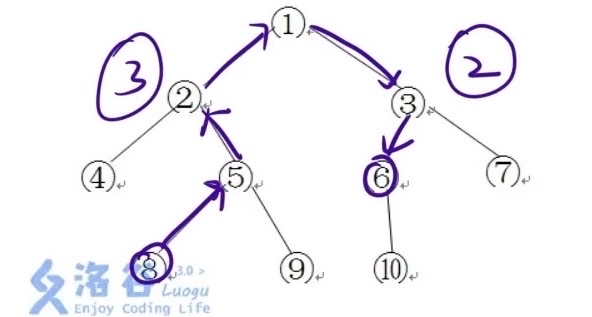
代码实现：

• 因为输入时，并没有明确输入的v为u的左节点还是右节点，只定义了v是u的子节点，所以 l、r 数组的实现方式不能用，得换成用vector数组创建起一棵有根树（输入特性）
• 求出深度，从叶节点往上统计；若当前结点的vector数组元素个数为0，则表明没有任何子节点，则为叶节点，遇到叶节点 return 1 要不然会把叶节点漏统计
• 求出宽度，用bfs统计队列中最大元素个数，每次输入一层元素销毁一层元素
• 求 x 到 y 的距离时，先从 x 向上爬，同时标记路径中所有点到 x 的距离，接下来 y 开始向上爬，当第一次遇到标记点时，更新结果（接下文）

---

求距离时如何让向上爬，求出各结点到源节点的距离？

因为无法确定源节点到哪一个结点停止，所以直接一路向上爬到根节点，统计源节点到根节点的所有距离情况

• fa[N]数组：fa[i] 表示 i 这个结点的父亲是谁
• dist[N]数组：dist[i] 表示 i（父节点） 这个结点到 x（子节点，最一开始是源节点） 的最短距离

使用时，dist[fa[x]] = dist[x]+1 表示父节点的到子节点的距离为子节点到子节点的子节点的距离+1，然后再把x更新为新的fa[x]（即其父亲）

---

如何标记 y 到相遇点的距离？

定义一个len，表示y到当前结点的距离；让y一步步往上爬（y=fa[y]），每爬一次len++，直到走到相遇点为止，判断是否相遇可以通过meet函数

代码：

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

const int N = 110;
vector<int> edges[N];
int ret=0;
int fa[N],dist[N];

int dfs(int root)
{
	if(!edges[root].size()) return 1;
	else if(edges[root].size()==1) return dfs(edges[root][0])+1;//只有1个孩子 
	else return max(dfs(edges[root][0]),dfs(edges[root][1]))+1;//有2个孩子 
}

void bfs()
{
	queue<int> q;
	q.push(1);
	
	while(q.size())
	{
			int sz = q.size();
			if(sz>ret)ret=sz;
		while(sz--)//开始存放下一层 
		{
			int root = q.front();q.pop();
			for(auto x:edges[root]) q.push(x);
		}
	}
}

bool meet(int x,int y)//判断是否相遇的函数(source为传值传参，所以不会被修改） 
{
	while(x!=1)
	{
		if(x==y)return true;
		else x=fa[x];	
	}	
	//当x、y都为整棵树的根节点时，需要特判
	if(x==y)return true;
	return false; 
} 

int main()
{
	//建树操作 
	int n;cin>>n;
	n--;
	while(n--)
	{
		int f,c;cin>>f>>c;
		edges[f].push_back(c);
		fa[c]=f; 
	}
	//求出深度
	cout<<dfs(1)<<endl;
	//求出宽度
	bfs();
	cout<<ret<<endl;
	int x,y;cin>>x>>y;
	int source = x; 
	while(x!=1)
	{
		dist[fa[x]]=dist[x]+1;
		x=fa[x];
	}
	int len=0;
	while(1)
	{
		if(!meet(source,y))
		{
			//表示没有相遇
			len++; 
			y=fa[y];
		}
		else break;
	}
	cout<<(dist[y]*2+len);
	return 0;
}