数据结构03——树

数据结构

树
二叉树

树

树的定义

树（Tree）：n （n>=0）个结点构成的有限集合

当n=0时，称为空树；

对于任意一棵非空树（n>0），它具备以下性质：

树中有一个称为"根（Root）"的特殊结点，用r表示；
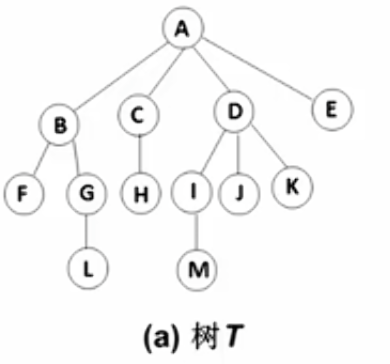
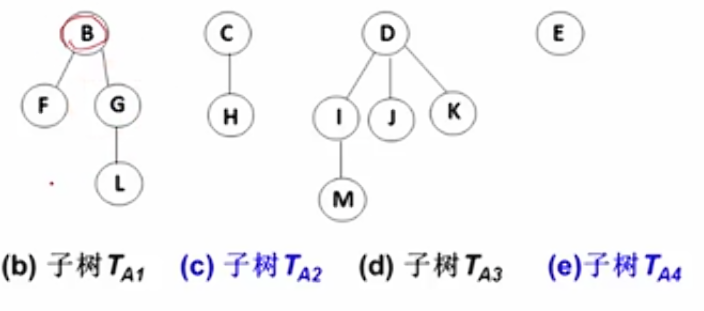
其余结点可分为m (m>0)个互不相交的有限集 T 1 ， T 2 ， . . . T m T_1，T_2，... T_m T1，T2，...Tm，其中每个集合本身又是一棵树，称为原来树的"子树（SubTree）"

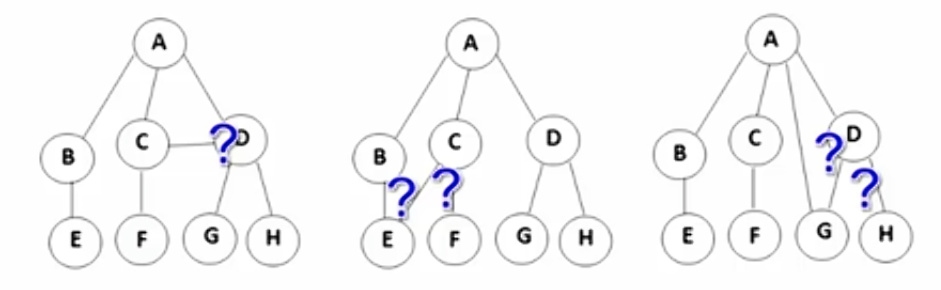
下图这些都不是树

子树是不相交的

除了根节点外，每个结点有且仅有一个父节点

一棵N个结点的树有N-1条边

树的基本术语

1.结点的度（Degree）：结点的子树个数

2.树的度：树的所有结点中最大的度数

3.叶结点（Leaf）：度为 0 的结点

4.父结点（Parent）：在树结构中，若结点 u 有一个或多个子结点（Child），则称结点 u 为这些子结点的父结点

5.子结点（Child）：若 A 结点是 B 结点的父结点，则称 B 结点是 A 结点的子结点；子结点也称孩子结点。

6.兄弟结点（Sibling）：具有同一父结点的各结点彼此是兄弟结点

路径和路径长度：从结点 n 1 n_1 n1 到 n k n_k nk 的路径为一个结点序列 n 1 ， n 2 ， . . . . n k n_1，n_2，....n_k n1，n2，....nk 路径所包含边的个数为路径的长度

8.祖先结点（Ancestor）：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点

9.子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙

10.结点的层次（Level）：规定根结点在 1 层，其它任一结点的层数是其父结点的层数加 1。

11.树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度。

注意：根节点没有父节点，叶子节点不可以作父节点

树的表示

用数组表示，不容易表示儿子和父亲这种关系

用链表表示，如下图

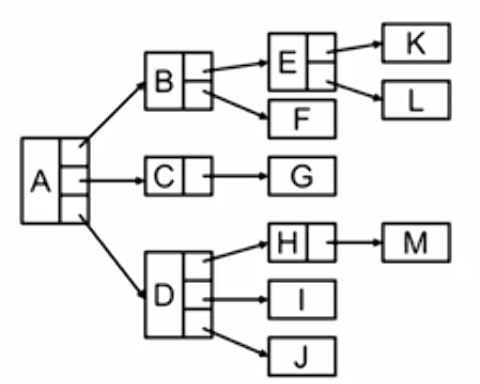
如果这个树的度为3

上图这种表示方式，需要空间为 3n。因为每个节点都需要3个指针，但实际只需要n+1个指针，因为只有n+1个边。这种浪费使得算法并不够好。

儿子兄弟表示法

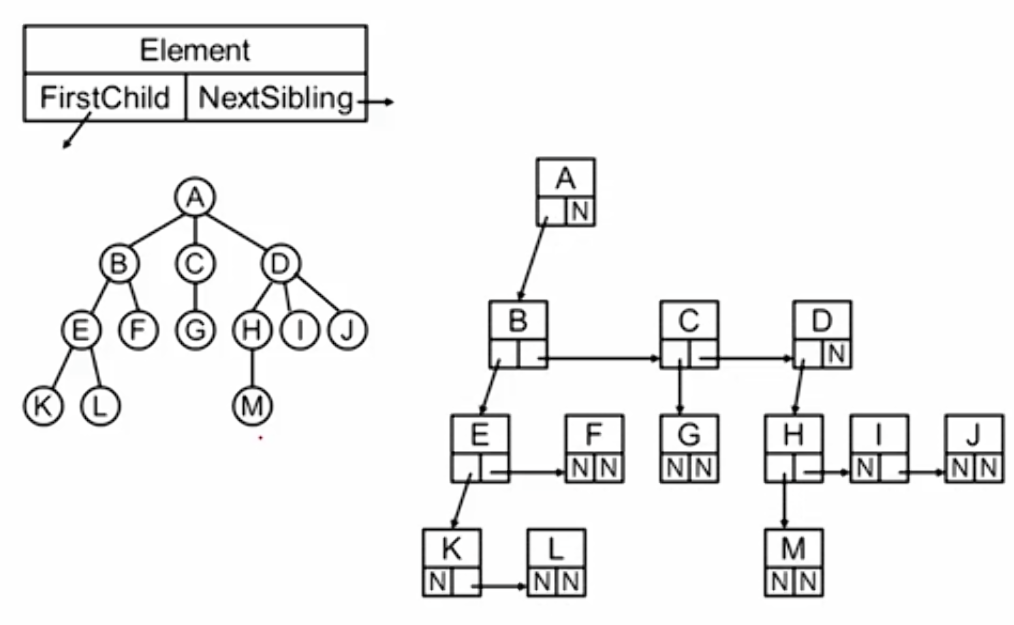
第一个指针指向自己的第一个子节点，第二个指针指向自己的右侧兄弟节点。

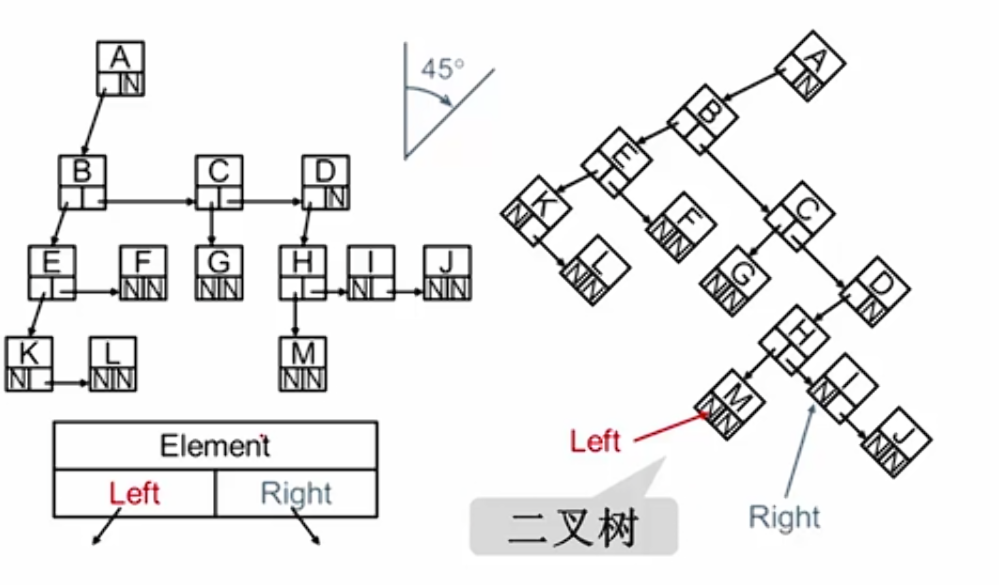
儿子兄弟法，也就是二叉树的变相来源

二叉树

二叉树的定义

二叉树 T T T：一个有穷的结点集合

这个集合可以为空

如果不为空，则它由根节点和称为其左子树 T L T_L TL和右子树 T R T_R TR的两个不相交的二叉树组成

二叉树的五种基本形态

二叉树的子树有左右顺序之分，一般度为2的树都没有。

特殊二叉树

完美二叉树就是全满

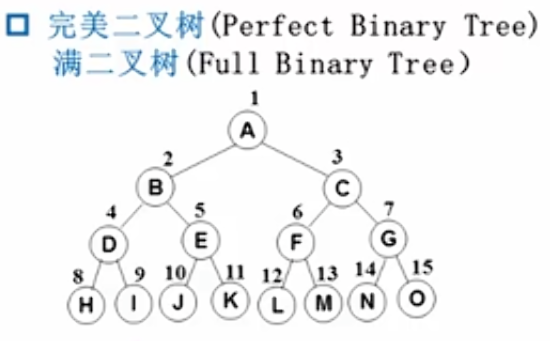
完全二叉树：

除最后一层外，其余各层的结点数都达到最大；

且最后一层的结点从左到右依次连续排列，中间不能有空缺。

二叉树几个重要性质

一个二叉树第 i i i 层的最大结点数为： 2 i − 1 ， i > = 1 2^{i-1}， i>=1 2i−1，i>=1

深度为 k k k的二叉树有最大结点总数为： 2 k − 1 ， k > = 1 2^k-1，k>=1 2k−1，k>=1

因为 1 + 2 + 2 2 + 2 3 + . . . . + 2 k − 1 = 2 k − 1 1+2+2^2+2^3+....+2^{k-1}=2^k-1 1+2+22+23+....+2k−1=2k−1

对于任何非空二叉树T，若 n 0 n_0 n0表示叶节点的个数、 n 2 n_2 n2是度为2的非叶结点个数，那么两者满足关系 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1

计算过程：

结点数： n 0 + n 1 + n 2 n_0+n_1+n_2 n0+n1+n2

边数： n 1 + 2 ∗ n 2 n_1+2*n_2 n1+2∗n2

结点数 = 边数+1

=>
n 0 + n 1 + n 2 = n 1 + 2 ∗ n 2 + 1 n_0+n_1+n_2=n_1+2*n_2+1 n0+n1+n2=n1+2∗n2+1

=>
n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1

二叉树的存储结构

顺序存储结构

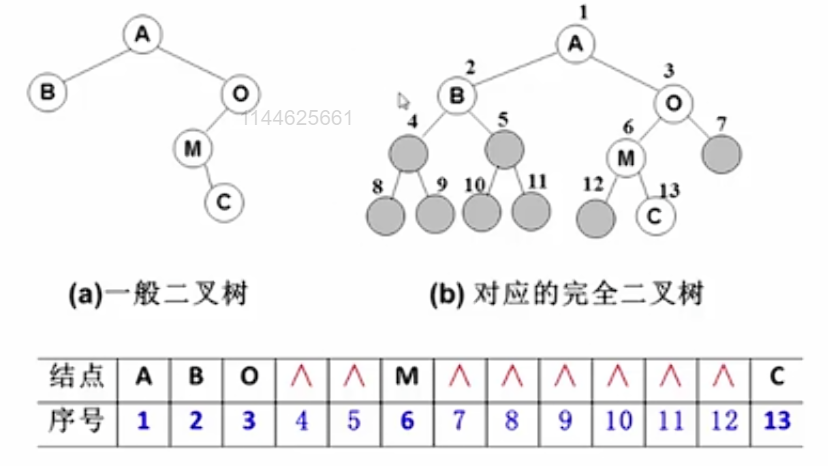
完全二叉树：按从上到下、从左到右顺序存储n个结点的完全二叉树的结点父子关系

非根结点（序号 i > 1）的父结点的序号是 ⌊ i / 2 ⌋ ⌊i / 2⌋ ⌊i/2⌋；

结点（序号为 i）的左孩子结点的序号是 2 i 2i 2i，（若 2 i ≤ n 2i ≤ n 2i≤n，否则没有左孩子）；

结点（序号为 i）的右孩子结点的序号是 2 i + 1 2i + 1 2i+1，（若 2 i + 1 ≤ n 2i + 1 ≤ n 2i+1≤n，否则没有右孩子）。

一般的二叉树也可以采用这种存储方式，但会造成空间的浪费

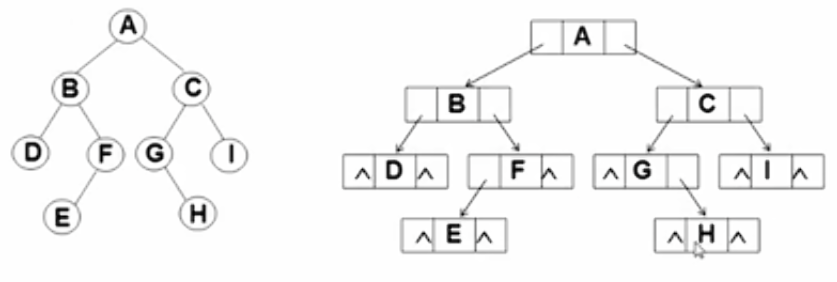
链表存储结构

c 复制代码

typedef struct TreeNode *BinTree;
typedef BinTree Position;
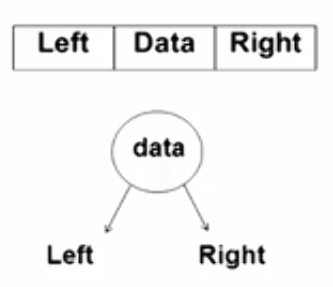
struct TreeNode{
	ElementType Data;
	BinTree Left;
	BinTree Right;
}

二叉树的遍历

递归遍历（最常见）

先序遍历

本质使用递归

遍历过程：
1 ◯ \textcircled{1} 1◯ 访问根节点
2 ◯ \textcircled{2} 2◯先序遍历左子树
3 ◯ \textcircled{3} 3◯先序遍历右子树

c 复制代码

void PreOrderTraversal (BinTree BT)
{
	if(BT) {
		printf("%d",BT->Data);
		PreOrderTraversal(BT->Left);
		PreOrderTraversal(BT->Right);
	}
}

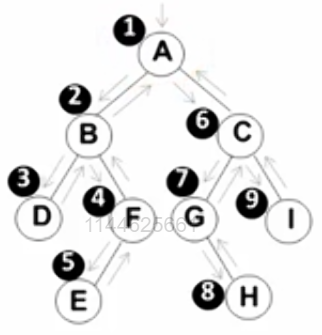
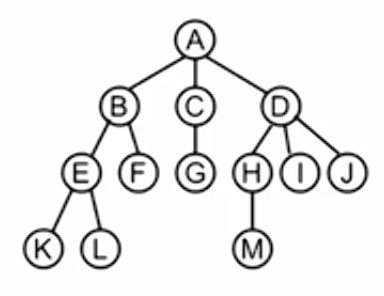
先序遍历结果：A B D F E C G H I

A ( B D F E ) ( C G H I )

中序遍历

本质使用递归

遍历过程：
1 ◯ \textcircled{1} 1◯中序遍历左子树
2 ◯ \textcircled{2} 2◯ 访问根节点
3 ◯ \textcircled{3} 3◯中序遍历右子树

c 复制代码

void InOrderTraversal (BinTree BT)
{
	if(BT) {
		InOrderTraversal(BT->Left);
		printf("%d",BT->Data);
		InOrderTraversal(BT->Right);
	}
}

中序遍历结果：D B E F A G H C I

( D B E F) A ( G H C I )

后序遍历

本质使用递归

遍历过程：
1 ◯ \textcircled{1} 1◯后序遍历左子树
2 ◯ \textcircled{2} 2◯后序遍历右子树
3 ◯ \textcircled{3} 3◯ 访问根节点

c 复制代码

void PostOrderTraversal (BinTree BT)
{
	if(BT) {
		PostOrderTraversal(BT->Left);
		PostOrderTraversal(BT->Right);
		printf("%d",BT->Data);
	}
}

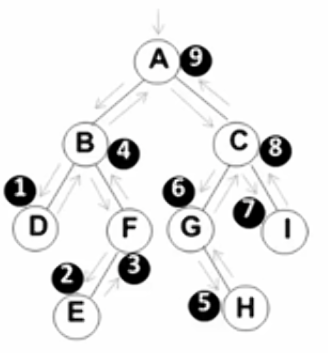
后序遍历结果：D E F B H G I C A

( D E F B ) ( H G I C ) A

注意：先序、中序、后序遍历过程中，经过结点的路线是一样的，只是访问各个结点的时机不同。

非递归遍历（用栈）

非递归先序遍历

在非递归实现中，深度优先遍历与二叉树的先序遍历类似，其访问操作均发生在结点入栈（被发现）时。

c 复制代码

void PreOrderTraversal( BinTree BT )
{
    BinTree T = BT;
    Stack S = CreatStack( MaxSize );   /* 创建并初始化堆栈 S */

    while ( T || !IsEmpty(S) ) {
        while ( T ) {                  /* 一直向左并将沿途结点压入堆栈 */
            printf("%5d", T->Data);    /* （访问）打印结点 */
            Push(S, T);
            T = T->Left;
        }

        if ( !IsEmpty(S) ) {
            T = Pop(S);                /* 结点弹出堆栈 */
            T = T->Right;              /* 转向右子树 */
        }
    }
}

非递归中序遍历

c 复制代码

void InOrderTraversal( BinTree BT )
{
    BinTree T = BT;
    Stack S = CreatStack( MaxSize );   /* 创建并初始化堆栈 S */

    while ( T || !IsEmpty(S) ) {
        while ( T ) {                  /* 一直向左并将沿途结点压入堆栈 */
            Push(S, T);
            T = T->Left;
        }

        if ( !IsEmpty(S) ) {
            T = Pop(S);                /* 结点弹出堆栈 */
            printf("%5d", T->Data);    /* （访问）打印结点 */
            T = T->Right;              /* 转向右子树 */
        }
    }
}

非递归后序遍历

后序遍历（Postorder Traversal：左 → 右 → 根）是非递归遍历里最难的一种。

常用的两种方式，第一种是最常见的，一个栈 + 最近访问结点（最经典、最爱考）

核心思想：引入一个指针 BinTree lastVisited = NULL;, 用于判断："右子树是否已经访问过"

算法规则

1.设当前结点为 T：一路向左入栈

2.查看栈顶结点：

如果右孩子存在且没访问过 → 转向右子树

否则 → 访问该结点并出栈

3.更新 lastVisited

c 复制代码

void PostOrder_OneStack(BinTree BT)
{
    Stack S = CreateStack(MaxSize);
    BinTree T = BT;
    BinTree lastVisited = NULL;

    while (T || !IsEmpty(S)) {

        while (T) {                 // 一直向左
            Push(S, T);
            T = T->Left;
        }

        T = Peek(S);                // 只看栈顶，不弹出

        if (T->Right && lastVisited != T->Right) {
            T = T->Right;           // 转向右子树
        } else {
            Pop(S);
            printf("%5d", T->Data); // 后序访问
            lastVisited = T;
            T = NULL;               // 防止重复进入
        }
    }
}

还有一种方式，使用两个栈，会造成空间的浪费，这里不赘述。

二叉树的层序遍历

用队列

和广度优先遍历基本相同

二叉树的层序遍历（Level-order Traversal）本质上就是图的广度优先搜索（BFS）在树结构上的特例。