1 单选题（每题 2 分，共 30 分）
第1题 下列关于类的说法，错误的是( )。
A. 构造函数不能声明为虚函数，但析构函数可以。
B. 函数参数如声明为类的引用类型，调用时不会调用该类的复制构造函数。
C. 静态方法属于类而不是某个具体对象，因此推荐用 类名::方法(...) 调用。
D. 不管基类的析构函数是否是虚函数，都可以通过基类指针/引用正确删除派生类对象。
解析：答案D。构造函数不能是虚函数（因为对象构造时虚表未建立），但析构函数可以（且应该声明为虚函数以实现多态安全），所以A说法无误；参数声明为引用（如 void foo(MyClass& obj)）时，传递的是对象别名，不会触发复制构造函数，只有值传递（如 void foo(MyClass obj)）才会调用复制构造函数，所以B说法正确；静态方法属于类本身，而非实例对象。推荐用 类名::方法(...) 调用（如 MyClass::staticFunc()），这能明确区分静态与实例方法，所以C说法合理；关键问题 ：如果基类析构函数不是虚函数 ，通过基类指针删除派生类对象时，只会调用基类析构函数，导致派生类资源泄露（如内存泄漏）。正确做法是：当基类可能被继承时，必须声明虚析构函数 （如 virtual ~Base() {}），所以D说法错误。故选D。
第2题 假设变量 veh 是类 Car 的一个实例，我们可以调用 veh.move() ，是因为面向对象编程有( )性质。
|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│class Vehicle { 2│private: 3│ string brand; 4│ 5│public: 6│ Vehicle(string b) : brand(b) {} 7│ 8│ void setBrand(const string& b) { brand = b; } 9│ string getBrand() const { return brand; } 10│ 11│ void move() const { 12│ cout << brand << " is moving..." << endl; 13│ } 14│}; 15│ 16│class Car : public Vehicle { 17│private: 18│ int seatCount; 19│ 20│public: 21│ Car(string b, int seats) : Vehicle(b), seatCount(seats) {} 22│ 23│ void showInfo() const { 24│ cout << "This car is a " << getBrand() 25│ << " with " << seatCount << " seats." << endl; 26│ } 27│}; |
A. 继承 (Inheritance) B. 封装 (Encapsulation)
C. 多态 (Polymorphism) D. 链接 (Linking)
解析：答案A。由Vehicle 类创建Car 类，即Car 类通过 class Car : public Vehicle 继承了 Vehicle 类（第16行）。move() 方法是 Vehicle 类中定义的公共方法（第11-13行），而 Car 类没有重写它 。因此，Car 的实例 veh 自动继承了 Vehicle 的 move() 方法，所以能直接调用 veh.move()。继承允许派生类（如 Car）复用基类（如 Vehicle）的属性和方法，无需重复代码。这里 veh.move() 能运行，正是因为 Car 继承了 Vehicle 的 move() 实现，体现了OOP的"代码复用"特性。封装关注数据隐藏（如 brand 是 private），但调用 move() 是方法访问，与封装无关；多态需要虚函数重写move()方法（如 virtual void move()），但 move() 不是虚函数，Car 也未重写它，因此不涉及多态；链接不是OOP标准性质，它属于编译/系统概念，与本题无关。故选A。
第3题 下面代码中 v1 和 v2 调用了相同接口 move() ，但输出结果不同，这体现了面向对象编程的( )特性。
|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│class Vehicle { 2│private: 3│ string brand; 4│ 5│public: 7│ Vehicle(string b) : brand(b) {} 7│ 8│ void setBrand(const string& b) { brand = b; } 9│ string getBrand() const { return brand; } 10│ 11│ virtual void move() const { 12│ cout << brand << " is moving..." << endl; 13│ } 14│}; 15│ 16│class Car : public Vehicle { 17│ private: 18│ int seatCount; 19│ 20│public: 21│ Car(string b, int seats) : Vehicle(b), seatCount(seats) {} 22│ 23│ void showInfo() const { 24│ cout << "This car is a " << getBrand() 25│ << " with " << seatCount << " seats." << endl; 26│} 27│ 28│ void move() const override { 29│ cout << getBrand() << " car is driving on the road!" << endl; 30│ } 31│}; 32│ 33│class Bike : public Vehicle { 34│public: 35│ Bike(string b) : Vehicle(b) {} 36│ 37│ void move() const override { 38│ cout << getBrand() << " bike is cycling on the path!" << endl; 30│ } 40│}; 41│ 42│int main() { 43│ Vehicle* v1 = new Car("Toyota", 5); 44│ Vehicle* v2 = new Bike("Giant"); 45│ 46│ v1->move(); 47│ v2->move(); 48│ 49│ delete v1; 50│ delete v2; 51│ return 0; 52│} |
A. 继承 (Inheritance) B. 封装 (Encapsulation)
C. 多态 (Polymorphism) D. 链接 (Linking)
解析：答案C。这道题的核心在于 多态（Polymorphism） 。相同调用：v1->move() 和 v2->move() 都是通过 Vehicle* 指针调用的同一接口 move()。不同输出：
v1（实际指向 Car）输出："Toyota car is driving on the road!"
v2（实际指向 Bike）输出："Giant bike is cycling on the path!"
基类 Vehicle 的 move() 声明为虚函数 virtual（第11行），派生类 Car 和 Bike 分别重写 override 了 move()（第28行、37行）。通过基类指针调用虚函数时，实际执行的是 对象重写的方法 （如 v1 实际是 Car，故调用 Car::move()）。这就是动态多态 ：同一接口（move()），不同行为（开车 vs 骑行）。Car/Bike 继承 Vehicle 是基础，但本题重点在于同一接口的差异化实现 ，而非单纯继承，而是虚函数+重写 实现多态；封装体现在 brand 私有化（第3行），但不体现在move()上；链接与编译/系统相关，与OOP特性无关。所以选C。
第4题 栈的操作特点是( )。
A. 先进先出 B. 先进后出 C. 随机访问 D. 双端进出
解析：答案B。栈（Stack）的操作特点是先进后出（FILO）， 最先进入栈的元素最后才能被取出（就像叠放的盘子：先放的在下层，最后才能拿到）。先进先出是队列（Queue） 的特性（如排队：先来先服务），栈不支持 。随机访问是数组（Array） 的特性，栈不支持 随机访问元素（只能访问栈顶元素）。双端进出是双端队列（Deque） 的特性（两端都可操作），栈不支持 。故选B。
第5题 循环队列常用于实现数据缓冲。假设一个循环队列容量为 5（即最多存放 4 个元素，留一个位置区分空与满），依次进行操作：入队数据1，2，3，出队1个数据，再入队数据4和5，此时队首到队尾的元素顺序是( )。
A. [2, 3, 4, 5] B. [1, 2, 3, 4] C. [3, 4, 5, 2] D. [2, 3, 5, 4]
解析：答案A。可以模拟循环队列的操作流程 ，逐步推演出结果。
初始化 ：如图1①队列空，front = 0, rear = 0（rear指向下一个插入位置）
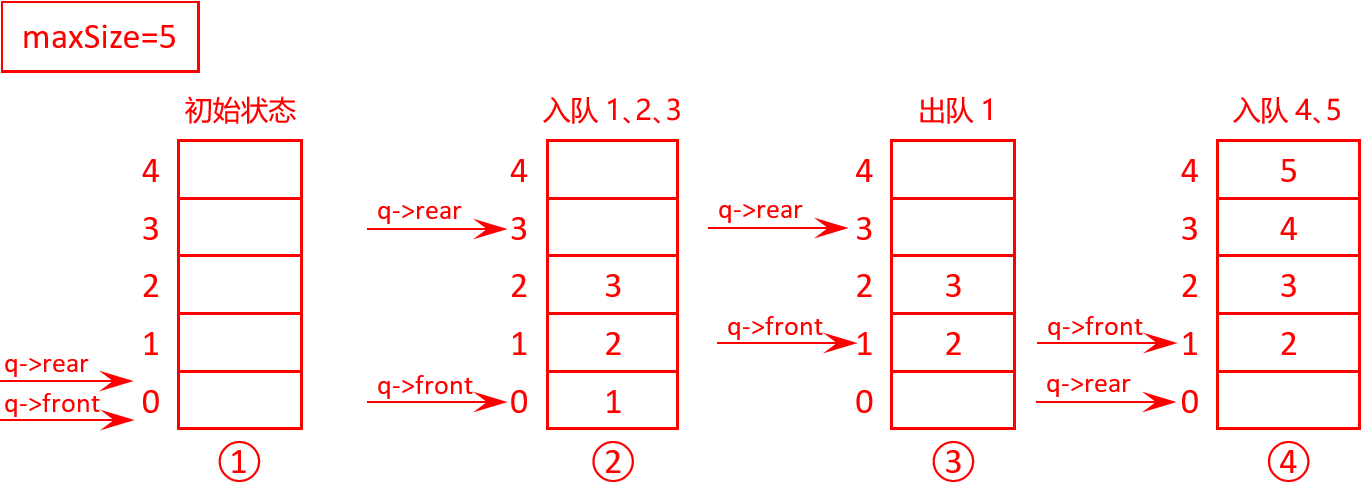
图1 程序生成的二叉树
入队1,2,3 ：如图1②入1 → rear = (0+1)%5 = 1；入2 → rear = (1+1)%5 = 2；入3 → rear = (2+1)%5 = 3。
出队1个 数据 ：如图1③移除队首(front=0位置的元素1)→ front = (0+1)%5 = 1
入队4和5 ：如图1④入4 → rear = (3+1)%5 = 4 ；入5 → rear = (4+1)%5 = 0 (循环到数组开头 )。此时队首到队尾的元素顺序是[2, 3, 4, 5]。故选A。
第6题 以下函数 createTree() 构造的树是什么类型？
|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│struct TreeNode { 2│int val; 3│TreeNode* left; 4│TreeNode* right; 5│TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 6│}; 7│ 8│TreeNode* createTree() { 9│TreeNode* root = new TreeNode(1); 10│root->left = new TreeNode(2); 11│root->right = new TreeNode(3); 12│root->left->left = new TreeNode(4); 13│root->left->right = new TreeNode(5); 14│return root; 15│} |
A. 满二叉树 B. 完全二叉树 C. 二叉排序树 D. 其他都不对
解析：答案B。按程序所建的二叉树结构如图2所示。
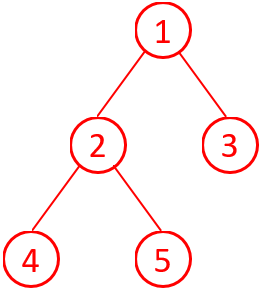
图2 程序生成的二叉树
满二叉树的定义为：一棵深度为k（层数为k）且具有2ᵏ - 1个节点的二叉树，其中所有层的节点数都达到最大值，即每个非叶节点都有两个子节点，且所有叶子节点都位于最深层。显然图2不符合满二叉树的定义。
完全二叉树的定义为：深度为k且有n个节点的二叉树，当且仅当其每个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时，称为完全二叉树。即除最后一层外，其他层的节点数都达到最大值，且最后一层的节点都集中在最左边。显然图2符合完全二叉树的定义。选B。
二叉排序树（又称二叉搜索树）的定义为：一棵空树或满足以下性质的二叉树：若左子树不为空，则左子树上所有节点的值均小于根节点的值；若右子树不为空，则右子树上所有节点的值均大于根节点的值；左、右子树也分别为二叉排序树，且没有键值相等的节点。显然图2不符合二叉排序树的定义。
第7题 已知二叉树的 中序遍历 是 [D, B, E, A, F, C]，先序遍历 是 [A, B, D, E, C, F]。请问该二叉树的后序遍历结果 是( )。
A. [D, E, B, F, C, A] B. [D, B, E, F, C, A] C. [D, E, B, C, F, A] D. [B, D, E, F, C, A]
解析：答案A。中序遍历先左树，再根节点，然后是右树，所有子树仍按先左树，再根，然后是右树规则遍历。选(前)序遍历先根节点，再是左树，然后是右树，所有子树仍按先根节点，再左树，然后是右树规则遍历
由先序遍历可知A是根节点，由中序遍历可知[D, B, E]是左树，[F, C]是右树。由先序遍历可知B是左子树的根节点，由中序遍历可知D是左树，E上右树，此时左、右树都只有一个点，整棵左子树结束。由先序遍历可知C上右子树的根节点，由中序遍历可知F是左树，此时左树只有一个点，无右树，整棵右子树结束。所构成的二叉树如图3所示。
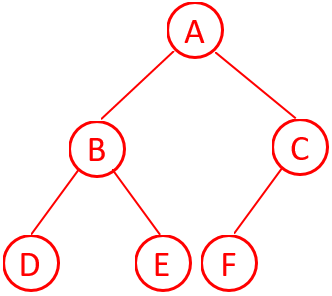
图3 按题意构建的哈夫曼树
后序遍历选是先左树、次右树、再根节点：D、E、B、F、C、A，故选A。
第8题 完全二叉树可以用数组连续高效存储，如果节点从 1 开始编号，则对有两个孩子节点的节点 i ，( )。
A. 左孩子位于 2i ，右孩子位于 2i+1
B. 完全二叉树的叶子节点可以出现在最后一层的任意位置
C. 所有节点都有两个孩子
D. 左孩子位于 2i+1 ，右孩子位于 2i+2
解析：答案A。在完全二叉树中，如果节点编号从1开始按层次遍历顺序编号，则对于任意节点i，左孩子节点的编号为 (2i)，右孩子节点的编号为 (2i+1)。故选A。
第9题 设有字符集 {a, b, c, d, e, f} ，其出现频率分别为 {5, 9, 12, 13, 16, 45} 。哈夫曼算法构造最优前缀编码，以下哪一组可能是对应的哈夫曼编码？（非叶子节点左边分支记作 0，右边分支记作 1，左右互换不影响 正确性）。
A. a: 00；b: 01；c: 10；d: 110；e: 111；f: 0
B. a: 1100；b: 1101；c: 100；d: 101；e: 111；f: 0
C. a: 000；b: 001；c: 01；d: 10；e: 110；f: 111
D. a: 10；b: 01；c: 100；d: 101；e: 111；f: 0
解析：答案B。以最小频率合并，频率左小右大为原则，建哈夫曼树如图4所示：
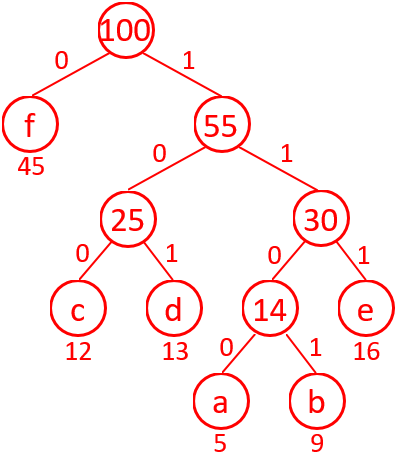
图4 按题意构建的哈夫曼树
a(5)和b(9)合并为14，c(12)和d(13)合并为25，14和e(16)合并为30，25和30合并为55，f(45)和55合并为100，构成图4所示哈夫曼树。
a: 1100，b: 1101，c: 100，d: 101，e: 111，f: 0
故选B。
第10题 下面代码生成格雷编码，则横线上应填写( )。
|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│vector grayCode(int n) { 2│if (n == 0) return {"0"}; 3│if (n == 1) return {"0", "1"}; 4│ 5│vector prev = grayCode(n-1); 6│vector result; 7│for (string s : prev) { 8│result.push_back("0" + s); 9│} 10│for (_______________) { // 在此处填写代码 11│result.push_back("1" + prev[i]); 12│} 13│return result; 14│} |
A. int i = 0; i < prev.size(); i++ B. int i = prev.size()-1; i >= 0; i--
C. auto s : prev D. int i = prev.size()/2; i < prev.size(); i++
解析：答案B。格雷编码要求相邻编码只有一位不同。递归生成n-1位编码后，通过镜像对称构造n位编码：前半部分（0前缀）保持原顺序；后半部分（1前缀）逆序添加，确保相邻编码差异。代码实现
for (int i = prev.size()-1; i >= 0; i--) { // 逆序遍历
result.push_back("1" + prev[i]);
}
逆序遍历prev，确保1前缀部分与0前缀部分对称
例如n=2时：
prev = {"00", "01", "11", "10"}
前半部分：{"000", "001", "011", "010"}
后半部分：{"110", "111", "101", "100"}（逆序添加）
A选项为正序遍历，会导致相邻编码差异超过一位，故错误；B选项为逆序遍历，符合镜像对称要求，故正确；C选项范围错误，无法遍历所有元素，故错误；D选项部分逆序，仅逆序一半元素，无法保证对称性，故错误。故选B。
第11题 请将下列树的深度优先遍历代码补充完整，横线处应填入( )。
|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│struct TreeNode { 2│ int val; 3│ TreeNode* left; 4│ TreeNode* right; 5│ TreeNode(int x): val(x), left(nullptr), right(nullptr) {} 6│}; 7│ 8│void dfs(TreeNode* root) { 9│ if (!root) return; 10│ ______ temp; // 在此处填写代码 11│ temp.push(root); 12│ while (!temp.empty()) { 13│ TreeNode* node = temp.top(); 14│ temp.pop(); 15│ cout << node->val << " "; 16│ if (node->right) temp.push(node->right); 17│ if (node->left) temp.push(node->left); 18│ } 19│} |
A. vector B. list C. queue D. stack
解析：答案D。这道题考察的是深度优先遍历(DFS)的非递归实现，初步判断横线处应填stack(栈)。看第10行声明 temp 后，第11行用temp.push()推入节点，第13行用temp.top()访问栈顶，第14行用temp.pop()弹出节点------这些操作是栈(stack)的典型方法(后进先出，LIFO)。非递归DFS依赖栈模拟递归调用栈。这里先推入根节点，循环中弹出节点并打印（前序遍历），再按"右子节点先入栈、左子节点后入栈"的顺序推入子节点（第16-17行）。这样左子节点先出栈处理，确保遍历顺序是根-左-右。
vector需用push_back()和back()/pop_back()，但代码用的是push()/top()不匹配，故A错误；list类似vector，无top()方法，操作不直接，B错误；queue用于广度优先搜索(BFS)，是先进先出(FIFO)，访问用front()而非top()，这里明显是DFS的栈行为，C错误。
故选D。
第12题 令𝑛是树的节点数目，下列代码实现了树的广度优先遍历，其时间复杂度是( )。
|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│void bfs(TreeNode* root) { 2│ if (!root) return; 3│ queue<TreeNode*> q; 4│ q.push(root); 5│ while (!q.empty()) { 6│ TreeNode* node = q.front(); 7│ q.pop(); 8│ cout << node->val << " "; 9│ if (node->left) q.push(node->left); 10│ if (node->right) q.push(node->right); 11│ } 12│} |
A. 𝑂(𝑛) B. 𝑂(log𝑛) C. 𝑂(𝑛²) D. 𝑂(2ⁿ)
解析：答案A。所有节点(包括 root)均被入队一次 (q.push())和出队一次 (q.front())。
每个节点的值输出(cout)和子节点检查(if 判断)均为常数时间操作𝑂(1)。总操作次数 = 入队𝑛次 + 出队𝑛次 + 访问节点值𝑛次 + 检查子节点2𝑛次（每个节点最多检查左右两个子节点）。
总时间 𝛵(𝑛) = 𝑛 × 𝑂(1) + 𝑛 × 𝑂(1) + 𝑛 × 𝑂(1) + 2 𝑛 × 𝑂(1) = 𝑂(𝑛)。故选A。
第13题 在二叉排序树(Binary Search Tree, BST)中查找元素50，从根节点开始：若根值为60，则下一步应去搜索：
A. 左子树 B. 右子树 C. 随机 D. 根节点
解析：答案A。二叉排序树满足以下性质的二叉树：左子树所有节点值均小于根节点，右子树所有节点值均大于根节点，且左右子树本身也为二叉排序树。由于根节点是60，查询元素为50，所示查询元素在左树。故选 A。
第14题 删除二叉排序树中的节点时，如果节点有两个孩子，则横线处应填入( )，其中findMax和findMin分别为寻找树的最大值和最小值的函数。
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│struct TreeNode { 2│ int val; 3│ TreeNode* left; 4│ TreeNode* right; 5│ TreeNode(int x): val(x), left(nullptr), right(nullptr) {} 6│}; 7│ 8│TreeNode* deleteNode(TreeNode* root, int key) { 9│ if (!root) return nullptr; 10│ if (key < root->val) { 11│ root->left = deleteNode(root->left, key); 12│ } 13│ else if (key > root->val) { 14│ root->right = deleteNode(root->right, key); 15│ } 16│ else { 17│ if (!root->left) return root->right; 18│ if (!root->right) return root->left; 19│ TreeNode* temp = ____________; // 在此处填写代码 20│ root->val = temp->val; 21│ root->right = deleteNode(root->right, temp->val); 22│ } 23│ return root; 24│} |
A. root->left B. root->right
C. findMin(root->right) D. findMax(root->left)
解析：答案C。当二叉排序树的节点有两个子节点时，删除策略是用中序后继或中序前驱来替代当前节点 。在题目提供的代码中，第21行显示删除操作是在右子树中进行的，因此这里选择的是中序后继 。中序后继是右子树中的最小节点，它的值大于当前节点但小于右子树中的其他所有节点，替换后仍然保持二叉排序树的性质。删除逻辑：当节点有两个子节点时，用右子树最小值(中序后继)替换当前节点值，再递归删除右子树中该最小值节点。所以选C。
第15题 给定𝑛个物品和一个最大承重为𝑊的背包，每个物品有一个重量𝑤𝑡[𝑖]和价值𝑣𝑎𝑙[𝑖]，每个物品只能选择放或不放。目标是选择若干个物品放入背包，使得总价值最大，且总重量不超过𝑊，则横线上应填写( )。
|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int knapsack(int W, vector& wt, vector& val, int n) { 2│ vector dp(W+1, 0); 3│ for (int i = 0; i < n; ++i) { 4│ for (int w = W; w >= wt[i]; --w) { 5│ ________________________ // 在此处填写代码 6│ 7│ } 8│ } 9│ return dp[W]; 10│} |
A. dp[w] = max(dp[w], dp[w] + val[i]);
B. dp[w] = dp[w - wt[i]] + val[i];
C. dp[w] = max(dp[w - 1], dp[w - wt[i]] + val[i]);
D. dp[w] = max(dp[w], dp[w - wt[i]] + val[i]);
解析：答案D。题目程序算法原理分析：这是经典的0-1背包问题的动态规划解法，采用空间优化的一维数组实现：dp[w]表示当前承重限制为w 时能获得的最大价值；外层循环 遍历每个物品 i，内层循环 从最大承重 W 倒序遍历到当前物品重量 wt[i]。
dp[w] = max(dp[w], dp[w - wt[i]] + val[i]) 的含义：dp[w]：不放入当前物品 i 时的最大价值(保持原值)，dp[w - wt[i]] + val[i]：放入当前物品 i 时的价值，即腾出 wt[i] 重量后的最大价值加上当前物品价值，max比较两种情况，选择价值更大的方案。
A选项：dp[w] + val[i] 错误，这会重复计算当前物品价值；B选项：缺少 max 比较，无法保证是最优解；C选项：dp[w-1] 无意义，重量减少1不一定对应有效状态。故选D。
2 判断题（每题 2 分，共 20 分）
第1题 当基类可能被多态使用，其析构函数应该声明为虚函数。
解析：答案正确。当基类可能被多态使用时，其析构函数应该声明为虚函数。这是因为如果通过基类指针删除派生类对象，非虚析构函数会导致派生类的析构函数不被调用，从而引发资源泄漏。声明为虚函数后，会触发正确的多态析构行为，先调用派生类析构函数，再调用基类析构函数。
第2题 哈夫曼编码是最优前缀码，且编码结果唯一。
解析：答案错误。哈夫曼编码是最优前缀码(其带权路径长度WPL最小)，但编码结果不唯一。当字符频率相同时，合并顺序不同会导致不同的树结构，从而产生不同的编码方案，但它们都能保证最优性。
第3题 一个含有100个节点的完全二叉树，高度为8。
解析：答案错误。一个含有100个节点的完全二叉树，如高度为h，则节点数在2ʰ⁻¹-2ʰ-1之间，2⁸⁻¹=128，2⁸-1=255。所以100个节点的完全二叉树不可能高度为8。
第4题 在C++ STL中，栈(std::stack)的pop操作返回栈顶元素并移除它。
解析：答案错误。C++ STL中std::stack的pop()操作仅移除栈顶元素，不返回任何值(返回类型为void)，要获取栈顶元素的值，应使用top()成员函数。
第5题 循环队列通过模运算循环使用空间。
解析：答案正确。循环队列通过模运算(取余)实现头尾相接的逻辑结构，当指针到达数组末尾时，会通过取模运算回到数组起始位置，从而循环使用已释放的空间。这是解决顺序队列"假溢出"问题的标准方法。
第6题 一棵有𝑛个节点的二叉树一定有𝑛-1条边。
解析：答案正确。根据树的性质，一棵有𝑛个节点的树，其边数恒为𝑛-1。这可以通过数学归纳法证明：当𝑛=1时边数为0；假设𝑛=𝑘时成立，则增加一个节点时需增加一条边使其连通且无环，此时边数为𝑘，符合(𝑘+1)-1。因此，对于任何𝑛个节点的树，边数都是𝑛-1。
第7题 以下代码实现了二叉树的中序遍历。输入以下二叉树，中序遍历结果是 4 2 5 1 3 6。
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│// 1 2│// / \ 3│// 2 3 4│// / \ \ 5│// 4 5 6 6│ 7│struct TreeNode { 8│ int val; 9│ TreeNode* left; 10│ TreeNode* right; 11│ TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 12│}; 13│ 14│void inorderIterative(TreeNode* root) { 15│ stack st; 16│ TreeNode* curr = root; 17│ 18│ while (curr || !st.empty()) { 19│ while (curr) { 20│ st.push(curr); 21│ curr = curr->left; 22│ } 23│ curr = st.top(); st.pop(); 24│ cout << curr->val << " "; 25│ curr = curr->right; 26│ } 27│} |
解析：答案正确。题目提供的代码使用栈模拟递归调用栈，先遍历左子树，再访问根节点，最后遍历右子树。对示例二叉树输出：4 2 5 1 3 6 (符合中序遍历规则：左-根-右)。
第8题 下面代码实现的二叉排序树的查找操作时间复杂度是𝑂(ℎ)，其中ℎ为树高。
|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│TreeNode* searchBST(TreeNode* root, int val) { 2│ while (root && root->val != val) { 3│ root = (val < root->val) ? root->left : root->right; 4│ } 5│ return root; 6│} |
解析：答案正确。题目所给程序代码实现二叉排序树(BST)的查找操作。BST性质：左子树值<根值<右子树值。程序中循环迭代：每次比较后直接跳转到左/右子树，最坏需遍历树高ℎ。最坏/平均情况：𝑂(ℎ)，最坏𝑂(𝑛)（退化为链表，此时ℎ=𝑛）
第9题 下面代码实现了动态规划版本的斐波那契数列计算，其时间复杂度是𝑂(2ⁿ)。
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int fib_dp(int n) { 2│ if (n <= 1) return n; 3│ vector dp(n+1); 4│ dp[0] = 0; 5│ dp[1] = 1; 6│ for (int i = 2; i <= n; i++) { 7│ dp[i] = dp[i-1] + dp[i-2]; 8│ } 9│ return dp[n]; 10│} |
解析：答案错误。题目所给程序是动态规划实现的斐波那契数列，其时间复杂度为：𝑂(𝑛)，并不是𝑂(2ⁿ)。
输入规模：输入为整数𝑛，目标是计算第𝑛个斐波那契数。初始化操作(第2~5行)：常数时间 𝑂(1)，第7行循环体𝑂(1)操作，循环体行6~8行共执行了n-1次，时间复杂度为𝑂(𝑛)。
第10题 有一排香蕉，每个香蕉有不同的甜度值。小猴子想吃香蕉，但不能吃相邻的香蕉。以下代码能找到小猴子吃到最甜的香蕉组合。
|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│// bananas：香蕉的甜度 2│void findSelectedBananas(vector& bananas, vector& dp) { 3│ vector selected; 4│ int i = bananas.size() - 1; 5│ 6│ while (i >= 0) { 7│ if (i == 0) { 8│ selected.push_back(0); 9│ break; 10│ } 11│ 12│ if (dp[i] == dp[i-1]) { 13│ i--; 14│ } else { 15│ selected.push_back(i); 16│ i -= 2; 17│ } 18│ } 19│ 20│ reverse(selected.begin(), selected.end()); 21│ cout << "小猴子吃了第: "; 22│ for (int idx : selected) 23│ cout << idx+1 << " "; 24│ cout << "个香蕉" << endl; 25│} 26│ 27│int main() { 28│ vector bananas = {1, 2, 3, 1}; // 每个香蕉的甜 29│ 30│ vector dp(bananas.size()); 31│ dp[0] = bananas[0]; 32│ dp[1] = max(bananas[0], bananas[1]); 33│ for (int i = 2; i < bananas.size(); i++) { 34│ dp[i] = max(bananas[i] + dp[i-2], dp[i-1]); 35│ } 36│ findSelectedBananas(bananas, dp); 37│ 38│ return 0; 39│} |
解析：答案正确。题目所给程序代码实现动态规划解决小猴子吃香蕉问题，核心功能包括：
动态规划数组初始化：dp[i]表示前i个香蕉中能吃到的最大甜度
状态转移方程：dp[i] = max(dp[i-1], bananas[i] + dp[i-2])，选择不吃当前或吃当前+跳过下一个
结果回溯：通过dp数组反向推导最优选择的香蕉索引
输出结果：打印小猴子选择的香蕉编号（从1开始计数）
3 编程题（每题 25 分，共 50 分）
3.1 编程题1
- 试题名称：划分字符串
- 时间限制：1.0 s
- 内存限制：512.0 MB
3.1.1题目描述
小A有一个由𝑛个小写字母组成的字符串𝑠。他希望将𝑠划分为若干个子串，使得子串中每个字母至多出现一次。例如，对于字符串street来说，str+e+e+t是满足条件的划分；而 s+tree+t不是，因为子串tree中e出现了两次。
额外地，小A还给出了价值𝑎₁, 𝑎₂, ..., 𝑎ₙ，表示划分后长度为𝑖的子串价值为𝑎ᵢ。小A希望最大化划分后得到的子串价值之和。你能帮他求出划分后子串价值之和的最大值吗？
3.1.2 输入格式
第一行，一个正整数𝑛，表示字符串的长度。
第二行，一个包含𝑛个小写字母的字符串𝑠。
第三行， 个正整数𝑎₁, 𝑎₂, ..., 𝑎ₙ，表示不同长度的子串价值。
3.1.3 输出格式
一行，一个整数，表示划分后子串价值之和的最大值。
3.1.4 样例
3.1.4.1 输入样例1
|----------------------------|
| 1│6 2│street 3│2 1 7 4 3 3 |
3.1.4.2 输出样例1
|------|
| 1│13 |
3.1.4.3 输入样例2
|------------------------------------|
| 1│8 2│blossoms 3│1 1 2 3 5 8 13 21 |
3.1.4.4 输出样例2
|-----|
| 1│8 |
3.1.5 数据范围
对于40%的测试点，保证1≤𝑛≤10³。
对于所有测试点，保证1≤𝑛≤10⁵，1≤𝑎ᵢ≤10⁹。
3.1.6 编写程序
编程思路：这道题使用动态规划(Dynamic Programming)。贪心在---般情况下不能保证正确。如样例2，随子串长度增加，子串价值是增加的(1 1 2 3 5 8 13 21)，对字符串blossoms，会拆成blos + som + s，价值为3+2+1=6，不如每个字符一个子串，价值8*1=8更高。
由于数据量1≤𝑛≤10⁵，只能采用𝑂(𝑛)、𝑂(𝑛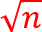
)或𝑂(𝑛log𝑛)的方法。本方法采用标准的自底向上DP，加上位掩码(mask)来快速判断某---段子串中是否有重复字母，并在发现重复时剪枝(break)，从而把时间复杂度控制在𝑂(26𝑛)级别。
由于只有小写字母，子串中每个字母用第1~26位置1的32位整数mask表示，a为1(1<<0)，b为2(1<<1)，c为4(1<<2)，...，z为2²⁵(1<<25)。如子串中已存在某字母，则mask中对应位置1，设cur为当前字母的位置置1值，则mask & cur为1则字母重复。
核心代码：
for(int i=1; i<=n; i++){
int mask = 0;
for(int j=i; j; j--){
int cur = 1 << (s[j-1] - 'a'); // s[j-1] - 'a'为第j个字母的序号0~25
if (mask & cur) break;
mask |= cur;
f[i] = max(f[i], f[j - 1] + a[i - j + 1));
}
}
外层i ：表示在求f[i]，也就是前缀s[1..i]的最优值(注意代码中s用的是索引从0开始和a用的是索引从1开始)。
mask ：用32位整数的位表示法记录当前子串里已经出现的字母(a对应第0位置1，b对应第1位置1，......，z对应第25位置1)。这样检测重复和加入新字母都能用位运算𝑂(1)完成。
内层j从i向前遍历，尝试把s[j..i]当成最后---个子串：
cur = 1 << (s[j-1] - 'a')：当前字符对应的位(0~25)，cur当前字符对应的位置1；
if (mask & cur) break; ：如果该位已在mask中，说明s[j..i]有重复字母，更往前的j会使子串更长，且仍包含这个重复字符，因此向前继续尝试更小j没必要------可以break(剪枝)；否则把该字母加入mask，然后更新f[i] = max(f[i], f[j-1] + a[i- j+1])，i- j+1为子串长度。
． f[0]默认为0。最终答案是f[n]。
动态规划的四个要素： 1)状态(State)，设f[i]为前i个字符(s[1..i])能取得的最大价值和。这是标准的"前缀最优"定义。2)转移(Transition)，对于f[i]，枚举最后---个子串s[j..i] (1≤j≤i)且要求s[0..i-1]每个字母不重复：f[i]=max(f[j-1]+a[i-j-1)如果j≤i, s[j..i]无重复，也就是：最后这个子串要么从某个j开始，把前缀s[0..j-2]的最优f(j-1)加上这个子串的值a[len]，所有可行的j取最大值。3)初始条件(Basacases)，f[0] = 0(空串价值为0)。4)计算顺序(Order)，自底向上：i从1到n，对每个i内部j从i递减到1(遇到重复直接break)。因为f[i]依赖f[i-1]，而j-1<i保证这些状态已被计算过。完整代码如下：
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 5; // n≤10⁵
int n;
char s[N]; // s字符串用字符数组
int a[N]; // n个长度为𝑖的子串价值为𝑎ᵢ
long long f[N]; // 𝑎ᵢ≤10⁹，f[i]为前i个字符(s[1..i])能取得的最大价值和
int main() {
cin >> n;
cin >> s; // s中只有小写字母，如含空格要用cin.getline()
for (int i = 1; i <= n; i++) // a索引(下标)从1开始，s索引(下标)从0开始
cin >> a[i];
for (int i = 1; i <= n; i++) {
int mask = 0;
for (int j = i; j; j--) {
int cur = 1 << (s[j-1] - 'a'); // s[j-1] - 'a'为第j个字母的序号0~25
if (mask & cur) break; // 第j个字符重复，则结束(剪枝)
mask |= cur; // 将第j个字符标记在mask中(指定位置1)
f[i] = max(f[i], f[j - 1] + a[i - j + 1]); // i-j+1为子串长度
}
}
cout << f[n]; // 当i为n时便是结果
return 0;
}3.2 编程题2
- 试题名称：货物运输
- 时间限制：1.0 s
- 内存限制：512.0 MB
3.2.1题目描述
A国有𝑛座城市，依次以1,2,...,𝑛编号，其中1号城市为首都。这𝑛座城市由𝑛-1条双向道路连接，第𝑖条道路(1≤𝑖≤𝑛)连接编号为𝑢ᵢ, 𝑣ᵢ的两座城市，道路长度为𝑙ᵢ。任意两座城市间均可通过双向道路到达。
现在A国需要从首都向各个城市运送货物。具体来说，满载货物的车队会从首都开出，经过一座城市时将对应的货物送出，因此车队需要经过所有城市。A国希望你设计一条路线，在从首都出发经过所有城市的前提下，最小化经过的道路长度总和。注意一座城市可以经过多次，车队最后可以不返回首都。
3.2.2 输入格式
第一行，一个正整数𝑎，表示A国的城市数量。 接下来𝑛-1行，每行三个整数𝑢ᵢ, 𝑣ᵢ, 𝑙ᵢ，表示一条双向道路连接编号为𝑢ᵢ, 𝑣ᵢ的两座城市，道路长度为𝑙ᵢ。
3.2.3 输出格式
一行，一个整数，表示你设计的路线所经过的道路长度总和。
3.2.4 样例
3.2.4.1 输入样例1
|-----------------------------|
| 1│4 2│1 2 6 3│1 3 1 4│3 4 5 |
3.2.4.2 输出样例1
|------|
| 1│18 |
3.2.4.3 输入样例2
|-----------------------------------------------------|
| 1│7 2│1 2 1 3│2 3 1 4│3 4 1 5│7 6 1 6│6 5 1 7│5 1 1 |
3.2.4.4 输出样例2
|-----|
| 1│9 |
3.2.5 数据范围
对于30%的测试点，保证1≤𝑛≤8。
对于另外30%的测试点，保证仅与一条双向道路连接的城市恰有两座。
对于所有测试点，保证1≤𝑛≤10⁵，1≤𝑢ᵢ, 𝑣ᵢ≤𝑛，1≤𝑙ᵢ≤10⁹。
3.2.6 编写程序
编程思路：这道题树的最远距离节点(边权和最大)搜索问题。先看样例1：
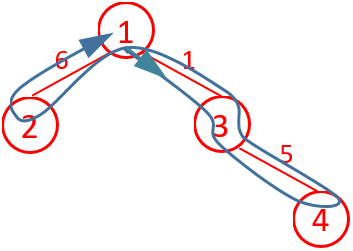
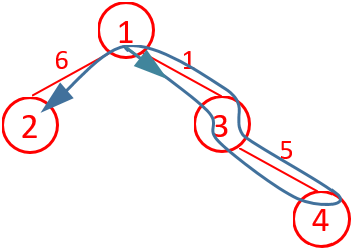
图 5 从 1 号根节点出发返回根节点 图 6 从 1 号根节点出发不返回根节点
按样例1数据构造的树如图5所示，如从根节点1出发返回根节点，则每条边都得走两遍。由于车队最后可以不返回首都(根节点)，求从首都(根节点)出发经过所有城市的前提下，最小化经过的道路长度总和，那就在返回首都(根节点)的基础上减去从根节点去往最远节点的距离，如图6所示，从1号出发到3，再从3出发到4，返回4，返回1，从1号出发到2，路程是1+5+5+1+6=18=(6+1+5)*2-6。由于此样例从1到6距离是6，从1到4距离也是6，所以走法不是唯一的，结果是相同的。表明：每条边走两次减去从根节点到最远节点的距离就是结果。因此问题变成求从根节点到最远距离的节点的距离，可用深度优先(dfs)遍历节点，记录距离，然后求最大距离。
读取数据的时间复杂度为𝑂(𝑛)，深度优先(dfs)遍历𝑛个节点𝑛-1条边的时间复杂度为𝑂(𝑛+𝑛-1)→𝑂(𝑛)，求最大距离的时间复杂度为𝑂(𝑛)，总体时间复杂度为𝑂(𝑛)，不会超时。
参考程序代码如下：
cpp
#include<iostream>
using namespace std;
const int MAXN = 1e5 + 5;
int n, head[MAXN], nxt[MAXN * 2], to[MAXN * 2], tot = 0;
long long d[MAXN], w[MAXN * 2], ans = 0;
void add(int x, int y, int z) { // 构建树
to[++tot] = y; // 边终点。tot为边的编号，每条来去两个编号
w[tot] = z; // 此边长度
nxt[tot] = head[x]; // 边起点编号
head[x] = tot; // 边起点节点编号(双向边，每个节点编两次，x⇋y)
}
void dfs(int u, int fa) { // 深度优先求从u单向到最后节点的距离
for (int i = head[u]; i; i = nxt[i]) {
if (to[i] == fa ) continue; // 如到达节点是父节点(非单向)
d[to[i]] = d[u] + w[i]; // 计算距离
dfs(to[i], u); // 递归直到to[i]=0, 无节点结束
}
}
int main() {
cin >> n; // 节点数(城市数)
int u, v, l;
for (int i = 1; i < n ; ++i) { // n-1条双向道路(双向边)
cin >> u >> v >> l;
add(u, v, l); // 添加u到v的边
add(v, u, l); // 因为双向，再添加v到u的边
ans += l * 2; // 每条边走两遍
}
dfs(1, 0); // 从1号首都(根节点)开始，父节点0，1均可
long long max_len = 0; // 最长路径长度(根节点到最远节点距离)
for (int i = 1; i <= n; ++i ) max_len = max(max_len, d[i]); // 求max_len
cout << ans - max_len; // ans为返回首都(根节点)的距离。
return 0;
}