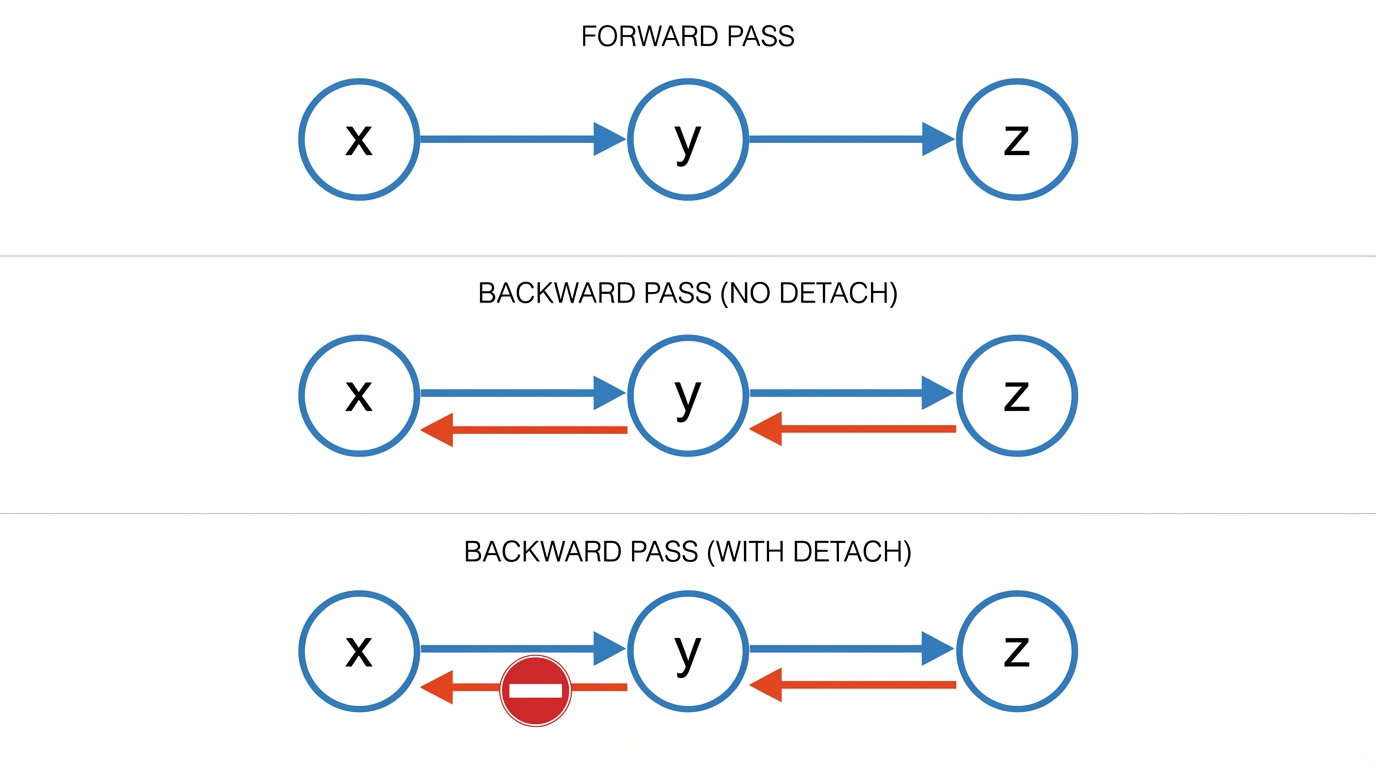
一、Detaching Computation:分离计算图中的梯度传播
在使用自动微分进行模型训练时,我们有时希望将部分计算从计算图中"摘除",使其在反向传播阶段不再参与梯度计算。
例如,设 yyy 是 xxx 的函数,zzz 又同时依赖于 xxx 和 yyy。
y=f(x),z=g(x,y) y = f(x),z = g(x,y) y=f(x),z=g(x,y)
zzz同时显式依赖 xxx,又通过yyy隐式依赖 xxx。
在标准的链式法则下,zzz 关于 xxx 的梯度为:
dzdx=∂g(x,y)∂x+∂g(x,y)∂y⋅dydx \frac{dz}{dx} = \frac{\partial g(x, y)}{\partial x} + \frac{\partial g(x, y)}{\partial y} \cdot \frac{dy}{dx} dxdz=∂x∂g(x,y)+∂y∂g(x,y)⋅dxdy
但在某些场景下,我们希望将 yyy 视为常数 ,只关注 xxx 对 zzz 的"直接影响",即人为令:dydx=0\frac{d y}{d x} = 0dxdy=0
这正是 detach() 的核心思想:主动切断计算图中的梯度路径。
1. 一个直观的示例
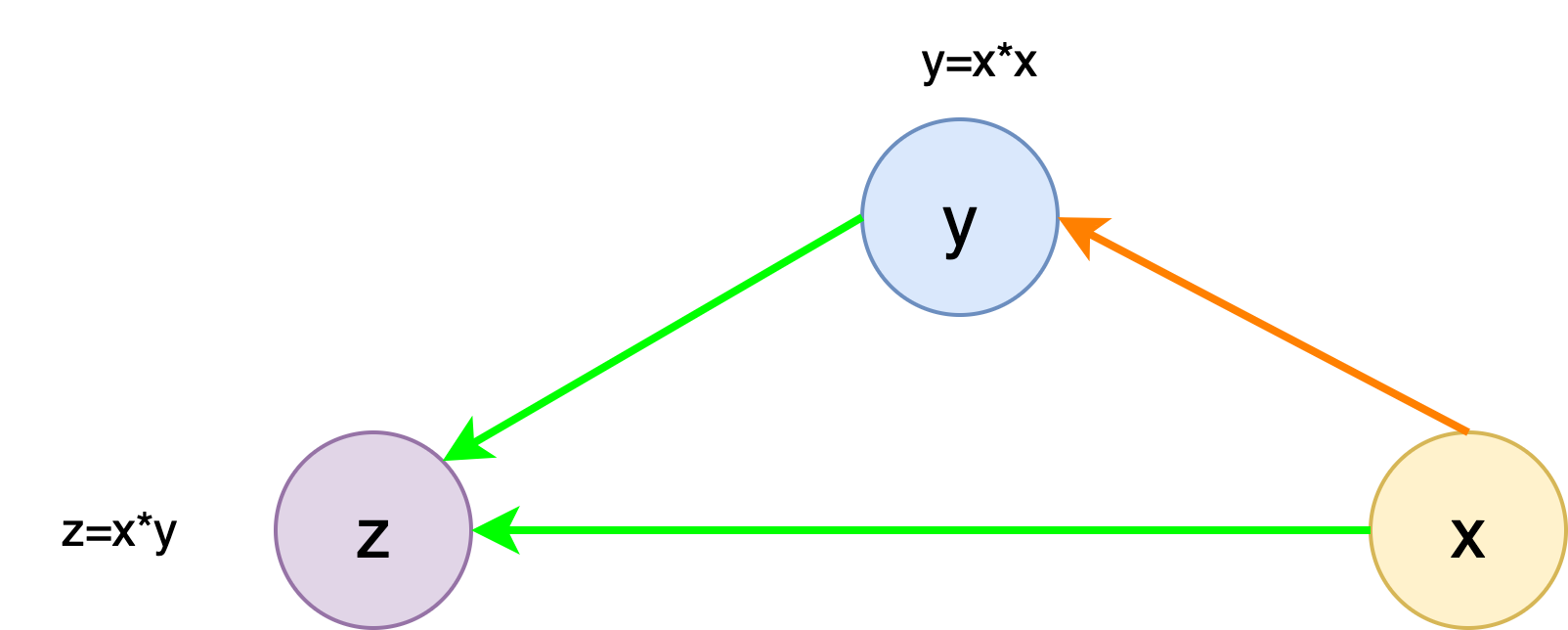
设:y=x2,z=x⋅yy = x^2, z=x \cdot yy=x2,z=x⋅y。如果按照完整的计算图进行反向传播,则有:
z=x⋅y=x3dzdx=3x2 z = x \cdot y = x^3 \\ \frac{d z}{d x} = 3x^2 z=x⋅y=x3dxdz=3x2
-
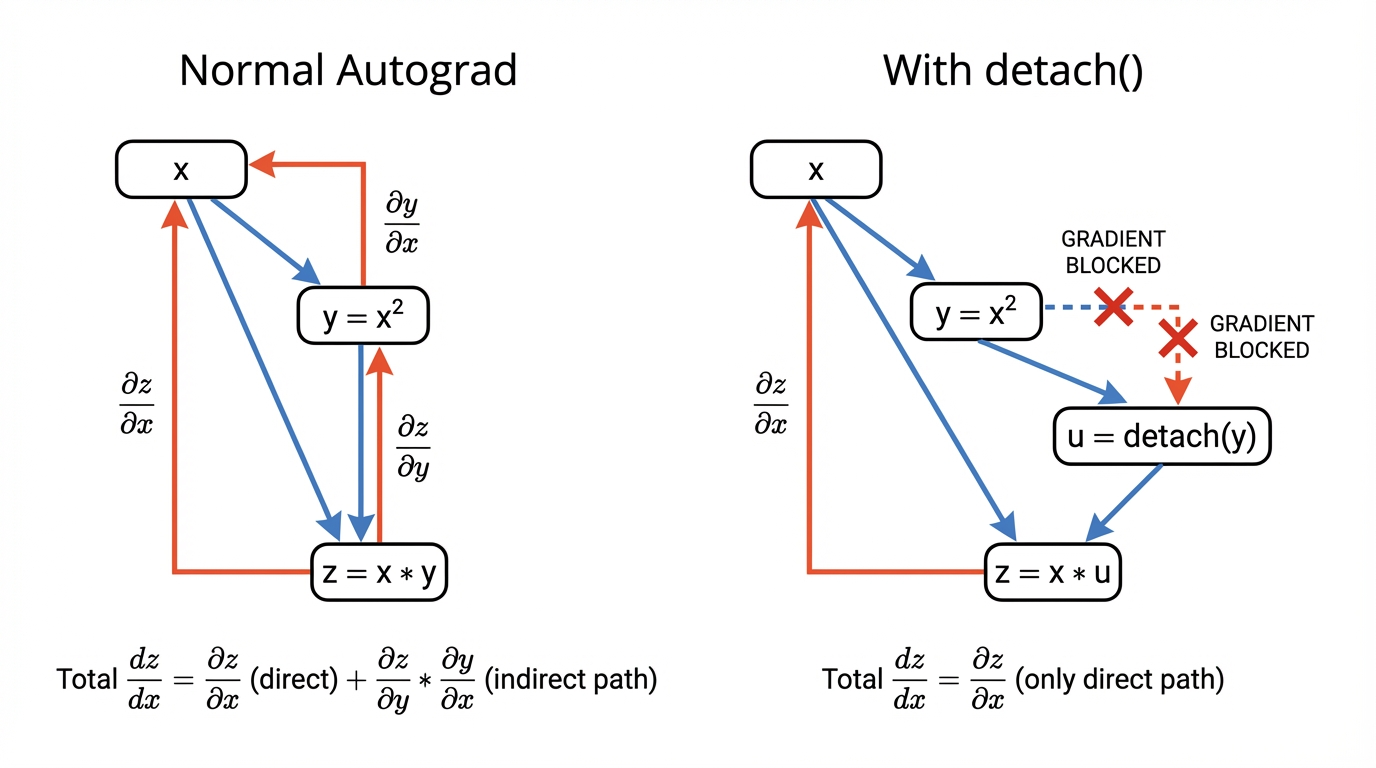
但现在我们希望在计算 zzz 的梯度时,不通过 yyy 反向传播到 xxx 。此时,可以构造一个新的变量 uuu:
- uuu 的数值与 yyy 相同
- 但 uuu 不再携带 yyy 的计算图信息
-
在 PyTorch 中,这可以通过
detach()实现。python>>> x.grad.zero_() tensor([0., 0., 0., 0.]) >>> y = x * x >>> u = y.detach() >>> z = u * x >>> z.sum().backward() >>> x.grad == u tensor([True, True, True, True])此时:
z=u⋅x,∂z∂x=u z = u \cdot x, \frac{\partial z}{\partial x} = u z=u⋅x,∂x∂z=u 可以看到,梯度结果为 uuu,而不是 3x23x^23x2。
-
这是因为,调用
detach()后,PyTorch 会返回一个新的 Tensor:- 与原 Tensor 共享底层数据
- 但其
grad_fn被置为None requires_grad=False,不再参与反向传播
2. detach 不会破坏原有计算图
需要强调的是:detach() 只会影响从它开始的新分支 ,并不会破坏原始 Tensor 的计算图。因此,仍然可以对 yyy 本身进行反向传播:
python
>>> x.grad.zero_()
tensor([0., 0., 0., 0.])
>>> y.sum().backward()
>>> x.grad == 2 * x
tensor([True, True, True, True]) 这是因为:
y = x * x的计算图仍然完整存在u = y.detach()只是创建了一个不再向后传播梯度的新视图
3. Python 控制流下的自动微分
需要注意的是,detach() 只会切断显式指定的梯度路径。在其他情况下,PyTorch 的自动微分系统依然可以在复杂的 Python 控制流下正常工作。
例如:
python
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c-
沿着这条实际执行的路径,
f中的所有操作都是线性的(乘常数):- 初始化:b0=2ab_0 = 2ab0=2a
- 多次循环:bi=2i×b0(i=1,2,⋯ ,n)b_i = 2^i \times b_0 (i = 1,2,\cdots, n)bi=2i×b0(i=1,2,⋯,n)
- 条件分支:c=bc = bc=b或c=100bc = 100bc=100b
-
该函数在数学上是分段线性的:对任意输入 aaa,都存在某个常数 kkk,使得 f(a)=k⋅af(a) = k \cdot af(a)=k⋅a。
其中,常数kkk由运行时控制流决定:
k={2n+1 if bn.sum()>0100×2n+1 if bn.sum()≤0 k = \begin{cases} 2^{n+1} & \text{ if } b_{n}.sum()>0 \\ 100 \times 2^{n+1} & \text{ if } b_{n}.sum() \le 0 \end{cases} k={2n+1100×2n+1 if bn.sum()>0 if bn.sum()≤0
python
>>> a = torch.randn(size=(), requires_grad=True)
>>> d = f(a)
>>> d.backward()
>>> a.grad
tensor(4096.)
>>> d / a
tensor(4096., grad_fn=<DivBackward0>) 这说明:即使计算图的构建依赖于 while、if 等 Python 控制流,PyTorch 仍然可以正确地记录运算并计算梯度。
二、从计算图角度理解detach
1. 从计算图中"摘取"一个Tensor
detach():把一个 Tensor 从计算图中"摘下来",使其后续操作不再参与反向传播。
detach()之后的 tensor- 不再有 grad_fn
- 不会影响模型参数的梯度计算
2. 计算图对比
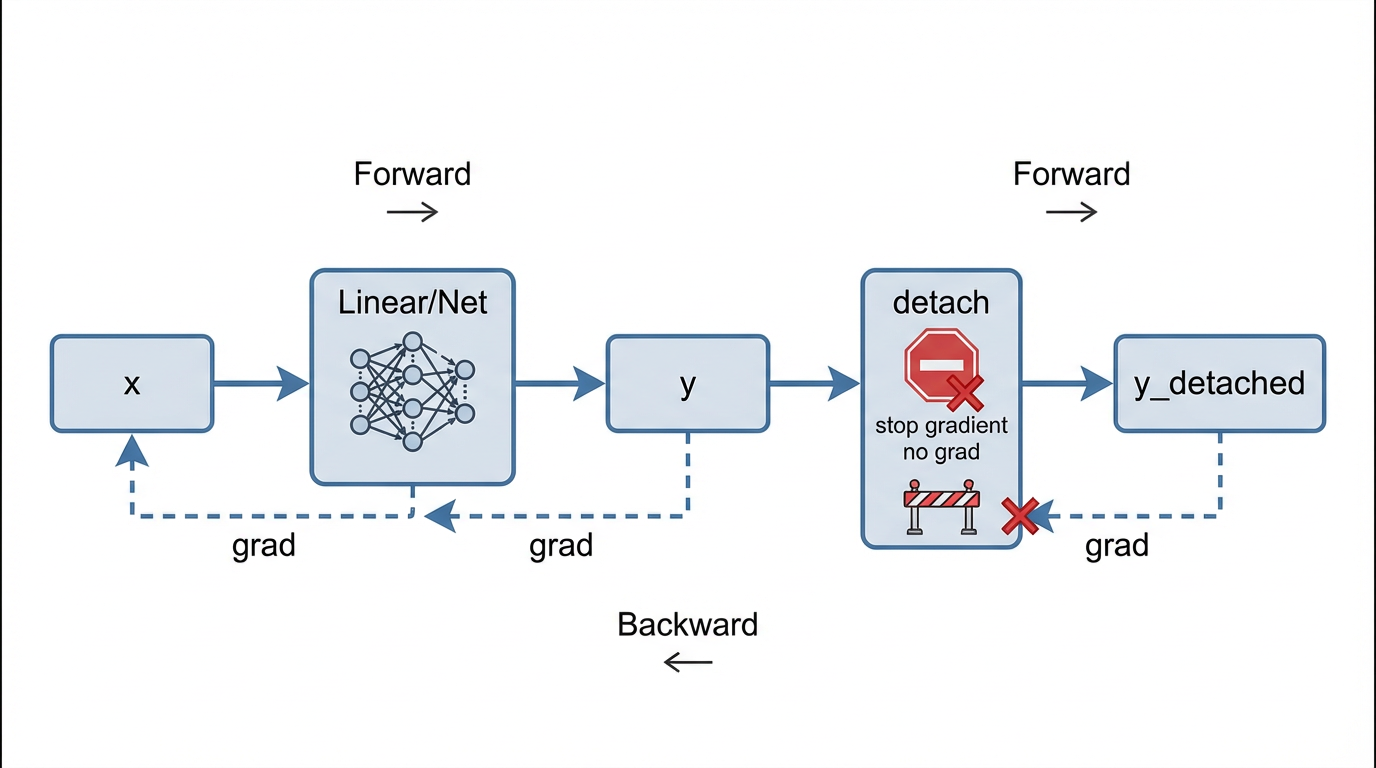
(1) 正常前向传播(训练阶段)
y = net(x) 对应的计算图为:
x ──▶ net ──▶ y
▲
计算图y录了完整的计算历史loss.backward()时,梯度会沿图反向传播
(2) 使用 detach()
y_detached = y.detach()。
计算图变为:
x ──▶ net ──▶ y y_detached
▲ ❌ 无计算图y_detached是一个新的 Tensor- 与
y共享数据,但不共享计算图 - 对
y_detached的任何操作,都不会反向影响net
三、Detach的典型应用场景
1. 推理 / 预测阶段:阻止梯度传播
python
pred = net(x)
pred_np = pred.detach().numpy()-
numpy()只能作用于不需要梯度的 Tensor -
若 Tensor 仍在计算图中,会触发运行时错误
bashRuntimeError: Can't call numpy() on Tensor that requires grad -
因此,
.detach().numpy()成为常见的标准写法。
在使用
torch.no_grad()的情况下,detach()往往是冗余的,但保留它可以提高代码的鲁棒性。
2. 冻结部分网络结构
在一些模型中,我们希望只训练网络的某一部分,例如:
python
h = encoder(x)
h = h.detach() # 冻结 encoder
out = decoder(h) 此时:
-
decoder的参数会被更新 -
encoder的参数梯度不会被计算这是
detach()在模型设计中非常经典且重要的用途。
3. detach、no_grad 与 eval 的区别(对比)
| 方法 | 作用范围 | 是否构建计算图 |
|---|---|---|
detach() |
单个 Tensor | 后续不参与 |
torch.no_grad() |
代码块 | 整段不构建 |
model.eval() |
模型行为 | 与梯度无关 |
四、小结
detach() 并不是"关闭梯度计算",而是在计算图中人为切断某些梯度路径。它允许我们在保持数值一致的前提下,精确控制哪些计算参与反向传播、哪些被视为常数。
这一机制在冻结子网络、构造辅助损失、以及推理阶段的数据处理等场景中都至关重要。
⚠️ 注意:由于
detach()返回的 Tensor 与原 Tensor 共享底层存储,对其进行 in-place 操作 可能会影响原 Tensor 的值,应谨慎使用。