一、时间复杂度
1.1定义
时间复杂度是算法执行次数(y)和数据总量(n)的关系,反映算法 "效率趋势"(不是具体执行时间)。
例:
y = a------------>y=1------------>O(1) 算法的执行次数与数据总量无关
y = an+b------------>y=n------------>O(n)
y = logan------------>y=logn------------>O(logn)
y = an²+bn+c------------>y=n²------------>O(n²)
效率排序:O(1)<O(logn)<O(n)<O(nlogn)<O(n2)
1.2真题练手
例题1:
int sum=0;
for(int i=1;i<n;i*=2)
for(int j=0;j<i;j++)
sum++;分析:
外层循环:i从 1 开始,每次 ×2,直到i≥n,执行次数是 log2n(比如 n=8 时,i=1、2、4,共 3 次);
内层循环:每次执行i次(i=1 时执行 1 次,i=2 时执行 2 次,...,i=2^k 时执行 2^k 次);
总执行次数:1+2+4+...+2log2n−1=2log2n−1=n−1;
时间复杂度:O(n)。
例题2:
int i=0;
while(i*i <=n)
i++;分析:
循环结束条件是i² >n,即i>√n,执行次数约为 ;
时间复杂度:O(√n)
例题3:
count=0;
for(k=1;k<=n;k*=2)
for(j=1;j<=n;j++)
count++;分析:
外层循环:k从 1 开始,每次 ×2,直到k>n,执行次数是 log2n(比如 n=8 时,k=1、2、4、8,共 4 次);
内层循环:每次固定执行n次;
总执行次数:log2n×n=nlog2n;
时间复杂度:O(nlogn)(对应选项 C)。
二、查找算法:从 "暴力" 到 "高效"
计算机 80% 的操作是 "查找",两种常见方式对比:
2.1无序数组查找(暴力遍历)
比如数组[5,7,4,2,0,3,1,6]找 "4":
只能从头到尾遍历,最坏情况执行 n 次;
时间复杂度:O(n)。

2.2折半查找(二分查找,仅适用于有序数组)
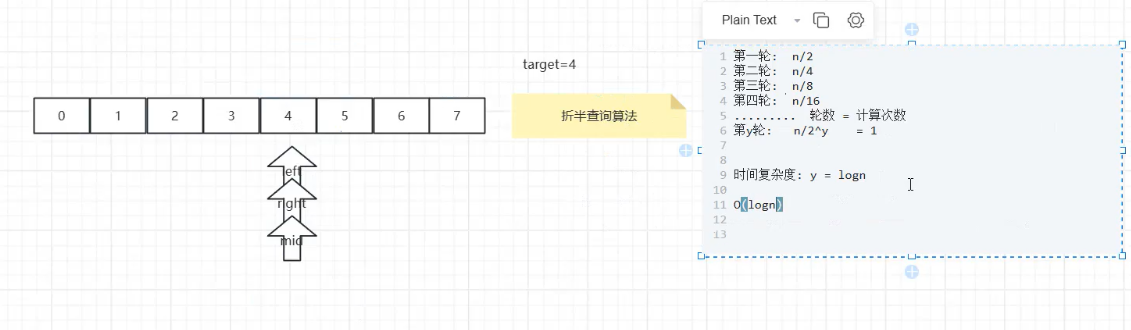
比如有序数组[0,1,2,3,4,5,6,7]找 "4":
步骤:先查中间位mid=3(对应值 3),比 4 小,再查右半部分的中间位mid=5(对应值 5),比 4 大,最后查中间位 4(找到目标);
执行次数:log2n(n=8 时执行 3 次);
时间复杂度:O(logn)。
三、排序算法:不同算法的效率差异
要想用折半查找,得先把数组排序 ------ 看几个经典排序的逻辑和复杂度。
3.1冒泡排序(O(n2))
核心逻辑 :前后元素对比,大的往后 "冒泡"。比如数组[4,2,0,3,1,5,6,7]:
第 1 轮:对比 (4,2)→交换,(4,0)→交换,...,最大的 "7" 移到末尾;
第 2 轮:对比剩下的元素,第二大的 "6" 移到倒数第二位;
最坏情况执行次数:1+2+...+(n−1)=n(n−1)/2;
时间复杂度:O(n2)。

3.2简单选择排序(O(n2))
核心逻辑 :每轮找最小值,和待排序部分的第一个元素交换。比如数组[0,1,2,3,5,4,7,6]:
第 1 轮:找最小的 "0",和第一个元素交换(已在正确位置);
第 2 轮:找剩下的最小 "1",和第二个元素交换;
无论数组是否有序,都要遍历找最小值,执行次数约n2/2;
时间复杂度:O(n2)。

3.3新增:插入排序(O(n2))
核心逻辑: 把数组分成 "已排序部分" 和 "未排序部分",每次从未排序部分取第一个元素 ,插入到已排序部分的合适位置(类似打扑克时整理手牌)。
举个例子,数组[4,2,0,3,1,5,6,7]:
第 1 轮:已排序部分是[4],取未排序的2,插入后变成[2,4];
第 2 轮:已排序部分是[2,4],取未排序的0,插入后变成[0,2,4];
第 3 轮:取未排序的3,插入到2和4之间,变成[0,2,3,4];
...... 直到所有元素插入完成。
最好情况:数组已经有序,每次插入只需要比较 1 次,总执行次数是n,时间复杂度O(n);
最坏情况:数组逆序,第i个元素需要比较i次(比如第 2 个元素比较 2 次,第 3 个比较 3 次...),总执行次数是1+2+...+(n−1)=n(n−1)/2,时间复杂度O(n2);
平均情况:时间复杂度也是O(n2)。

3.4 希尔排序(介于O(nlogn)和O(n2))
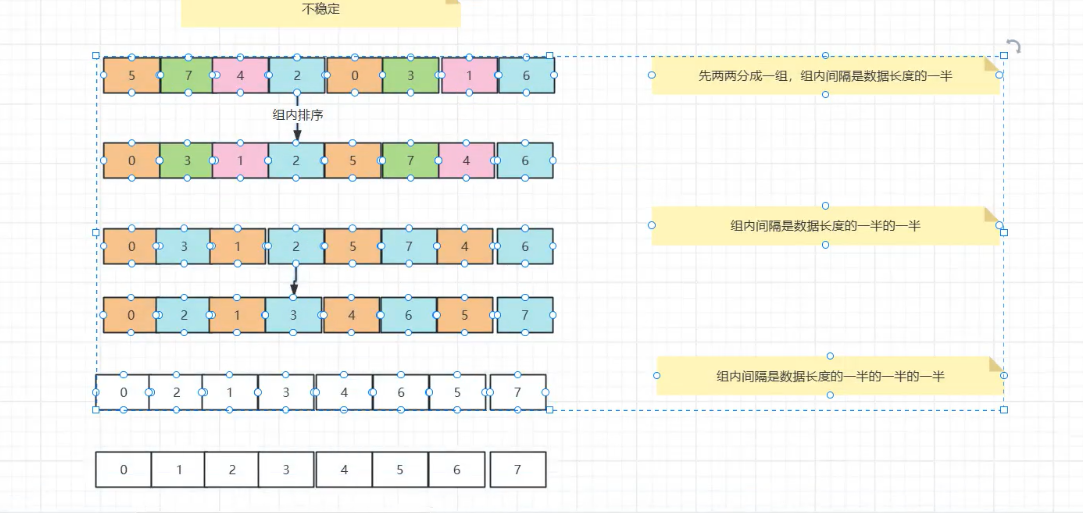
核心逻辑 :按 "间隔" 分组排序,逐步缩小间隔,最后用直接插入排序收尾。比如数组[5,7,4,2,0,3,1,6](长度 8):
第 1 轮:间隔 = 4,分成 4 组(5,0)、(7,3)、(4,1)、(2,6),组内排序后得到[0,3,1,2,5,7,4,6];
第 2 轮:间隔 = 2,分成 2 组(0,1,5,4)、(3,2,7,6),组内排序后得到[0,2,1,3,4,6,5,7];
第 3 轮:间隔 = 1,直接插入排序得到有序数组;
时间复杂度:和间隔选择有关,通常介于O(nlogn)和O(n2)之间。