【数据结构】栈和队列及相关算法题

王璐WL2025-12-17 8:24

文章目录

  • 1.栈
    • [1.1 概念与结构](#1.1 概念与结构)
    • [1.2 栈的实现](#1.2 栈的实现)
  • 2.队列
    • [2.1 概念与结构](#2.1 概念与结构)
    • [2.2 队列的实现](#2.2 队列的实现)
  • 3.栈和队列算法题
    • [3.1 有效的括号](#3.1 有效的括号)
    • [3.2 ⽤队列实现栈](#3.2 ⽤队列实现栈)
    • [3.3 ⽤栈实现队列](#3.3 ⽤栈实现队列)

1.栈

1.1 概念与结构

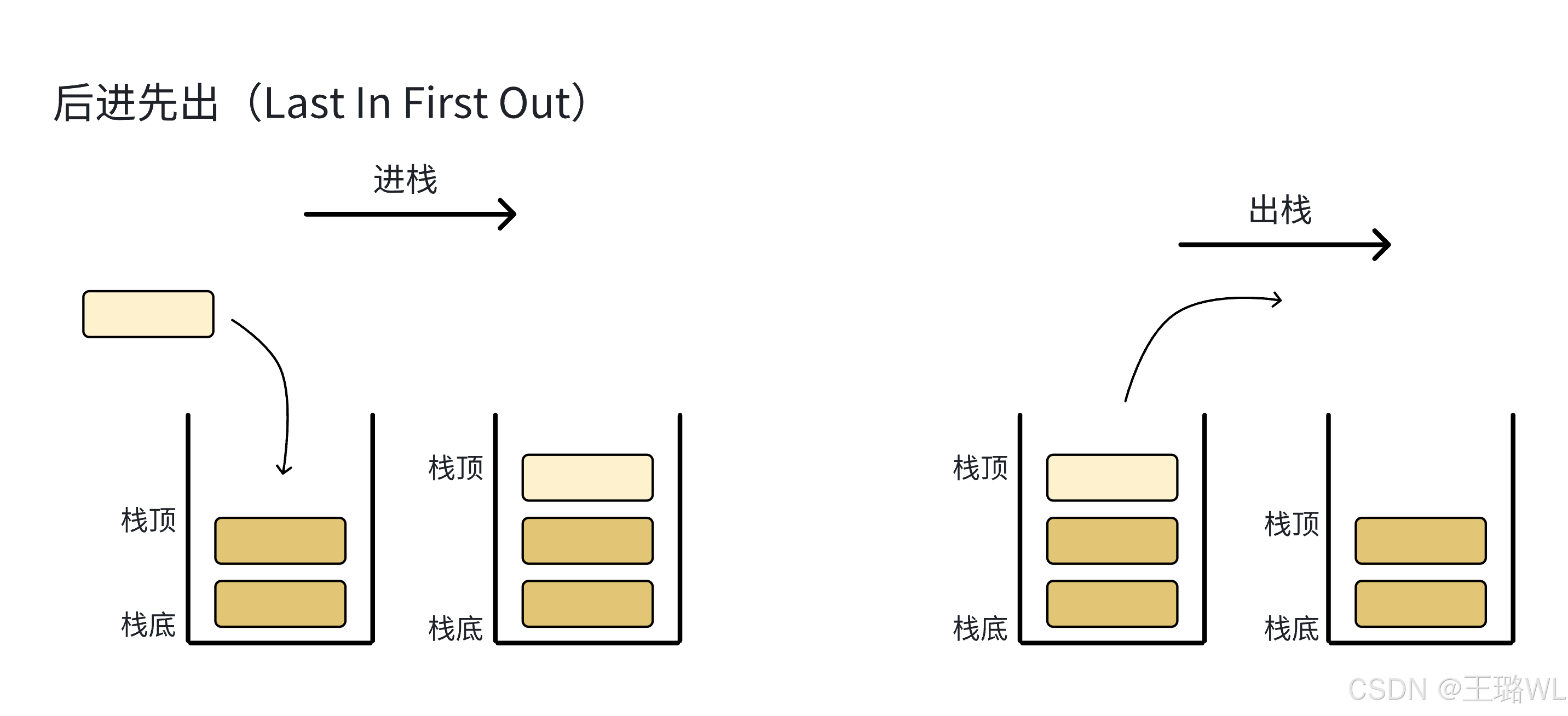
栈：⼀种特殊的线性表，其只允许在固定的⼀端进⾏插⼊和删除元素操作。进⾏数据插⼊和删除操作的⼀端称为栈顶，另⼀端称为栈底。栈中的数据元素遵守后进先出LIFO（LastInFirstOut）的原则。

压栈：栈的插⼊操作叫做进栈/压栈/⼊栈，⼊数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。 栈底层结构选型 栈的实现⼀般可以使⽤数组或者链表实现，相对⽽⾔数组的结构实现更优⼀些。因为数组在尾上插⼊数据的代价⽐较⼩。

1.2 栈的实现


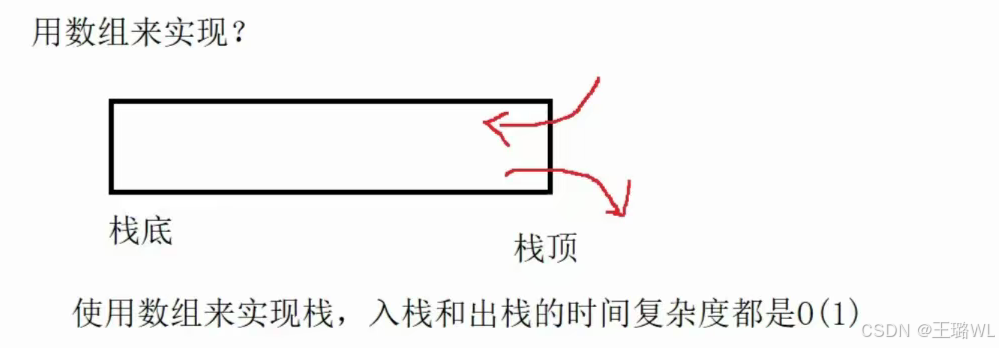
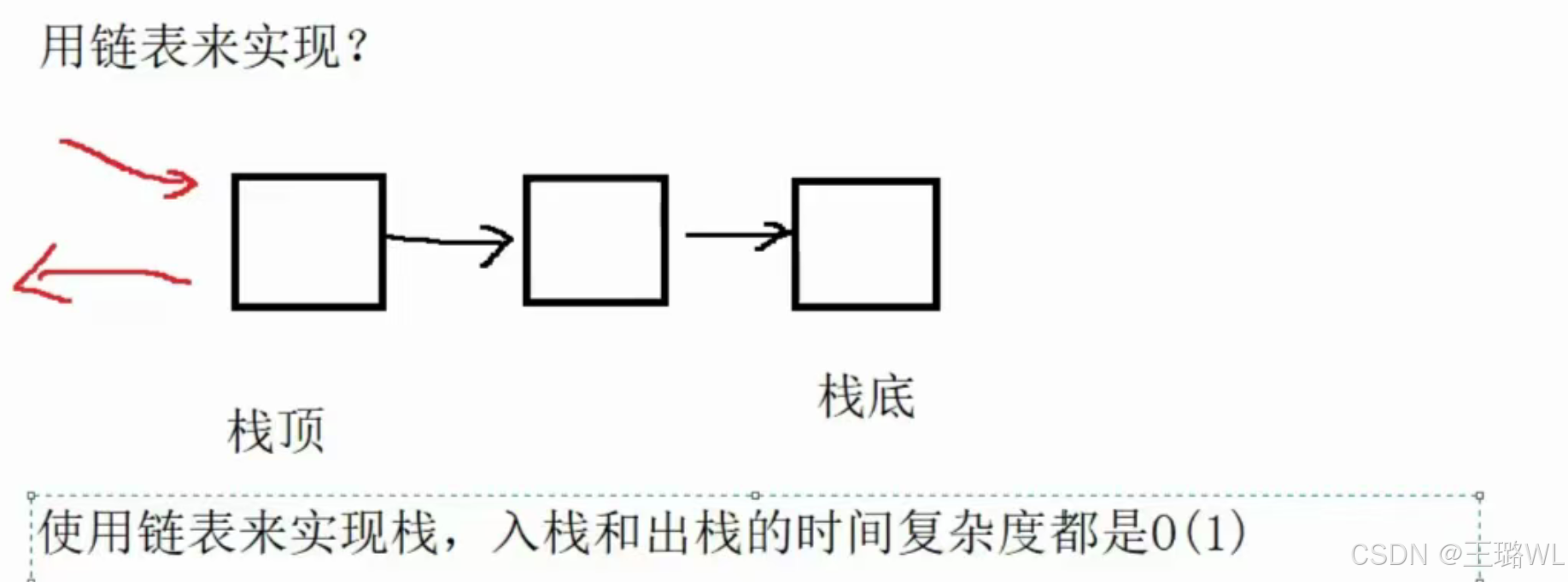
在时间复杂度相同情况下，假如要存放三个int类型，用底层数组实现只需三个整型空间，用链表则需三个结点

为什么顺序表不需要二级指针接收，单链表有时候需要

关键原因：顺序表只需要释放内部数组，不需要修改外部指针（具体细节可以自行查询）

c 复制代码 
//stack.h 
#include<stdio.h>
#include<assert.h>
typedef int STDataType; 
typedef struct Stack 
{ 
    STDataType* arr;//数组 
    int top;//有效数据的个数，也是栈顶 
    int capacity;//栈的空间大小
}ST; 
// 初始化栈 
void STInit(ST* ps); 
// 销毁栈 
void STDestroy(ST* ps); 
// ⼊栈 
void STPush(ST* ps, STDataType x); 
//出栈 
void STPop(ST* ps); 
//取栈顶元素 
STDataType STTop(ST* ps); 
//获取栈中有效元素个数 
int STSize(ST* ps); 
//栈是否为空 
bool STEmpty(ST* ps);
c 复制代码 
//stack.c
#include"Stack.h"
// 初始化栈 
void STInit(ST* ps)
{
    ps->arr=NULL;
    ps->top=ps->capacity=0;
}
// 销毁栈 
void STDestroy(ST* ps)
{
    if(ps->arr)
        free(ps->arr);
    ps->arr=NULL;
    ps->top=ps->capacity=0;
}
// ⼊栈 
void STPush(ST* ps, STDataType x)
{
    assert(ps);
    //先判断空间是否足够
    if(ps->top==ps->capacity)
    {
        //说明空间不够了需要增容
        int newCapacity=ps->capacity==0?4:2*ps->capacity;
        STDataType* tmp=(STDataType*)realloc(ps->arr,newCapacity*sizeof(STDataType));
        if(tmp==NULL)
        {
            perror("realloc");
            exit(1);
        }
        ps->arr=tmp;
        ps->capacity=newCapacity;
    }
    //空间足够
    ps->arr[ps->top++]=x;
}
//栈是否为空 
bool STEmpty(ST* ps)
{
    assert(ps);
    return ps->top==0;//必须有有效数据，如果top==0就直接返回
}
//出栈 
void STPop(ST* ps)
{
 	assert(!STEmpty(ps));
    ps->top--;
}
//取栈顶元素 
STDataType STTop(ST* ps)
{
    assert(!STEmpty(ps));
    return ps->arr[ps->top-1];
}
//获取栈中有效元素个数 
int STSize(ST* ps)
{
    assert(ps);//传的参数指针不为空就行，有效数据个数可以为0
    return ps->top;
}
c 复制代码 
//test.c
#include"Stack.h"
void test01()
{
    //初始化
    ST st;
    STInit(&st);
    
    //压栈
    STPush(&st,1);
    STPush(&st,2);
    STPush(&st,3);
    STPush(&st,4);
    
    //打印有效数据个数
    printf("size:%d\n", STSize(&st));
    
    //出栈
    STPop(&st);
    STPop(&st);
    STPop(&st);
    STPop(&st);
    
    //循环取
    while(!STEmpty(&st))
    {
        //取栈顶元素
        STDataType top=STTpop(&st);
        printf("%d ",top);
        STPop(&st);
    }
    printf("\n");
    
    //销毁
    STDesTroy(&st);
}
int main()
{
    test01();
    return 0;
}

2.队列

2.1 概念与结构

概念：只允许在⼀端进⾏插⼊数据操作，在另⼀端进⾏删除数据操作的特殊线性表，队列具有先进先出FIFO(FirstInFirstOut)

⼊队列：进⾏插⼊操作的⼀端称为队尾

出队列：进⾏删除操作的⼀端称为队头

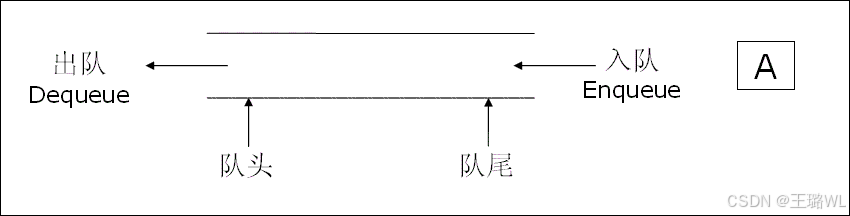
栈是先进的后出，队列是先进的先出

队列底层结构使⽤链表的结构实现更优⼀些。

2.2 队列的实现

c 复制代码 
//Queue.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int QDataType; 
//队列结点结构 
typedef struct QueueNode 
{ 
    QDataType data; 
    struct QueueNode* next; 
}QueueNode; 
//队列结构 
typedef struct Queue 
{ 
    QueueNode* phead;//指向队头结点的指针，所以变量类型是结点结构的指针 
    QueueNode* ptail;//指向队尾结点的指针 
    int size;//有效数据个数
}Queue; 
//初始化队列 
void QueueInit(Queue* pq); 
//销毁队列 
void QueueDestroy(Queue* pq); 
// ⼊队列，队尾 
void QueuePush(Queue *pq, QDataType x); 
// 出队列，队头 
void QueuePop(Queue* pq); 
//取队头数据 
QDataType QueueFront(Queue* pq); 
//取队尾数据 
QDataType QueueBack(Queue* pq); 
//队列判空 
bool QueueEmpty(Queue* pq); 
//队列有效元素个数 
int QueueSize(Queue* pq);
c 复制代码 
//test.c
#include"Queue.h"
void test01()
{
    Queue q;
    QueueInit(&q);
    QueuePush(&q,1);
    QueuePush(&q,2);
    QueuePush(&q,3);
    QueuePush(&q,4);
    
    QueuePop(&q);
    QueuePop(&q);
    QueuePop(&q);
    QueuePop(&q);
    
    printf("队头：%d\n",QueueFront(&q));
	printf("队尾：%d\n",QueueBack(&q));
	printf("有效数据个数：%d\n", QueueSize(&q));
}
int main()
{
    test01();
    return 0;
}
c 复制代码 
//Queue.c
#include"Queue.h"

//初始化
void QueueInit(Queue* pq)
{
    assert(pq);
    pq->phead=pq->ptail=NULL;
    pq->size=0;
}
// ⼊队列，队尾 
void QueuePush(Queue *pq, QDataType x)
{
    assert(pq);
    //创建值为x的结点
    QueueNode* newnode=(QueueNode*)malloc(sizeof(QueueNode));
    if(newnode==NULL)
    {
        perror("malloc");
        exit(1);
    }
    newnode->data=x;
    newnode->next=NULL;
    if(pq->phead==NULL)
    {
        pq->phead=pq->ptail=newnode;
    }
    else
    {
        //队列的尾指针的next指向newnode，再将尾指针指向newnode
    	pq->ptail->next=newnode;
    	pq->ptail=pq->ptail->next;
    }
    pq->size++;
}
//队列判空 
bool QueueEmpty(Queue* pq)
{
    assert(pq);
    return pq->phead==NULL;
}
// 出队列，队头 
void QueuePop(Queue* pq)
{
    assert(!QueueEmpty(pq));
    //队列中只有一个结点
    if(pq->phead==pq->ptail)
    {
        free(pq->phead);
        pq->phead=pq->ptail=NULL;
    }
    else
    {
        QueueNode* next=pq->phead->next;
        free(pq->phead);
        pq->phead=next;
    }
    pq->size--;
}
//取队头数据 
QDataType QueueFront(Queue* pq)
{
    assert(!QueueEmpty(pq));
    return pq->phead->data;
}
//取队尾数据 
QDataType QueueBack(Queue* pq)
{
    assert(!QueueEmpty(pq));
    return pq->ptail->data;
}
//队列有效元素个数 
int QueueSize(Queue* pq)
{
    assert(pq);
    return pq->size;
}
//销毁队列 
void QueueDestroy(Queue* pq);
{
    assert(pq);
    QueueNode* pcur=pq->phead;
    while(pcur)
    {
        QueueNode* next=pcur->next;
        free(pcur);
        pcur=next;
    }
    pq->phead=pq->ptail=NULL;
}

3.栈和队列算法题

3.1 有效的括号

题目链接

思路：如果是左括号就入栈，如果是右括号就取栈顶元素看是否匹配，若匹配成功，左括号出栈，继续查看下一个字符

c 复制代码 
//注意修改int为char
typedef char STDataType;
bool isValid(char* s)
{
    ST st;
    STInit(&st);
    char* pi=s;
    while(*pi)
    {
        //左括号就入栈
        if(*pi=='('||*pi=='['||*pi=='{')
        {
            STPush(&st,*pi);
        }
        else
        {
            //右括号，取栈顶比较，匹配就出栈，不匹配直接返回false      
            //特殊情况：第一个字符就是右括号，此时栈为空，不能直接取栈
            if(STEmpty(&st))
            {
                STDesTroy(&st);
                return false;
            }
            char top= STTop(&s);
            if((top=='('&&*pi!=')')||(top=='{'&&*pi!='}')||(top=='['&&*pi!=']'))
            {
                STDesTroy(&st);
                return false;
            }
            //本次匹配,匹配就出栈
            STPop(&st);
        }
        pi++;
    }
    //特殊情况
    //判断栈是否为空，为空（都出栈了）有效，非空（只有一个左括号）无效
    bool ret=STEmpty(&st)?true:false;
    STDesTroy(&st);
    return ret;
}

3.2 ⽤队列实现栈

题目链接

思路：入栈：往不为空的队列中插入数据

出栈：把不为空的队列中前size-1个数据挪到另一个队列，再将最后一个数据出队列（此时相当于出栈）

取栈顶：找不为空的队列，返回队尾数据

c 复制代码 
//将自己写的队列的代码复制粘贴
typedef struct{
    Queue q1;
    Queue q2;
}MyStack;
MyStack* myStackCreate()
{
    MyStack* pst=(MyStack*)malloc(sizeof(MyStack));
    QueueInit(&pst->q1);
    QueueInit(&pst->q2);
    return pst;
}
//入栈   
void myStackPush(MyStack* obj,int x)
{
    //往不为空的队列中插入数据
    //如果q1不为空，往q1中插入，否则插入q2
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}
int myStackPop(MyStack* obj)
{
    //找不为空队列
    Queue* emp=&obj->q1;
    Queue* noneEmp=&obj->q2;
    if(QueueEmpty(&obj->q2))
    {
        emp=&obj->q2;
        noneEmp=&obj->q1;
    }
    //不为空队列前size-1个数据挪到空队列
    while(QueueSize(noneEmp)>1)
    {
        //取队头，入另一个队列  
        QueuePush(emp,QueueFront(noneEmp));
        //出队头
        QueuePop(noneEmp);
    }
    //不为空队列数据出队
    int top=QueueFront(noneEmp);
    QueuePop(noneEmp);
    return top;
}
//取栈顶数据
int myStackTop(MyStack* obj)
{
    //找不为空队列,返回不为空队列的队尾数据
     if(!QueueEmpty(&obj->q1))
         return QueueBack(&obj->q1);
    else
        return QueueBack(&obj->q2);  
}
bool myStackEmpty(MyStack* obj)
{
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj)
{
    QueueDesTroy(&obj->q1);
    QueueDesTroy(&obj->q2);
    free(obj);
    obj=NULl;
}

3.3 ⽤栈实现队列

题目链接

思路思路 两个栈一个是pushST，一个是popST

入队列：往pushST插入数据

出队列：popST不为空直接出，否则将pushST中的数据先倒过去，再出数据

取队头：popST不为空直接取队头，否则将pushST中的数据先倒过去，再取队头

c 复制代码 
//将栈的代码复制粘贴在这
typedef struct {
    ST pushST;
    ST popST;
} MyQueue;
MyQueue* myQueueCreate() {
    MyQueue* pq=(MyQueue*)malloc(sizeof(MyQueue));
    STInit(&pq->pushST);
    STInit(&pq->popST);
    return pq;
}

void myQueuePush(MyQueue* obj, int x) {
    //往pushST中插入数据
    STPush(&obj->pushST,x);
}

int myQueuePop(MyQueue* obj) {
    //popST为空-----将pushST（不为空）导入到popST
    if(STEmpty(&obj->popST))
    {
        while(!STEmpty(&obj->pushST))
        {
            //取栈顶，入popST栈，出栈
            STPush(&obj->popST,STTop(&obj->pushST));
            STPop(&obj->pushST);
        }
    }
    //popST不为空直接出
    int top=STTop(&obj->popST);
    STPop(&obj->popST);
    return top;
}
int myQueuePeek(MyQueue* obj) {
    //popST为空-----将pushST（不为空）导入到popST
    if(STEmpty(&obj->popST))
    {
        while(!STEmpty(&obj->pushST))
        {
            //取栈顶，入popST栈，出栈
            STPush(&obj->popST,STTop(&obj->pushST));
            STPop(&obj->pushST);
        }
    }
    //popST不为空直接取
    int top=STTop(&obj->popST);
    return top;
}

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->popST)&&STEmpty(&obj->pushST);
}

void myQueueFree(MyQueue* obj) {
    STDesTroy(&obj->pushST);
    STDesTroy(&obj->popST);
    free(obj);
    obj=NULL;
}
相关推荐
麒qiqi5 小时前
Linux 线程（POSIX）核心教程
linux·算法
Zhi.C.Yue5 小时前
React 的桶算法详解
前端·算法·react.js
小热茶5 小时前
浮点数计算专题【五、 IEEE 754 浮点乘法算法详解---基于RISCV的FP32乘法指令在五级流水线的运行分析与SystemC实现】
人工智能·嵌入式硬件·算法·systemc
Giser探索家5 小时前
卫星遥感数据核心参数解析：空间分辨率与时间分辨率
大数据·图像处理·人工智能·深度学习·算法·计算机视觉
q_30238195565 小时前
破局路侧感知困境：毫米波雷达+相机融合算法如何重塑智能交通
数码相机·算法
Robert--cao5 小时前
人机交互（如 VR 手柄追踪、光标移动、手势识别）的滤波算法
人工智能·算法·人机交互·vr·滤波器
云青山水林5 小时前
算法竞赛从入门到跳楼（ACM-XCPC、蓝桥杯软件赛等）
c++·算法·蓝桥杯
LYFlied5 小时前
【每日算法】LeetCode138. 随机链表的复制
数据结构·算法·leetcode·链表
zore_c5 小时前
【C语言手撕算法】LeetCode-142. 环形链表 II（C语言）
c语言·数据结构·算法·leetcode·链表·推荐算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser08【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）09BongoCat - 跨平台键盘猫动画工具10安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）