机器学习高阶教程＜3＞统计学习理论进阶

你有没有过这样的经历：花了一周调参的模型，在训练集上准确率直奔99%，一到测试集就"翻车"到60%？对着混乱的误差曲线抓头发时，是不是忍不住想问：到底有没有一套理论，能让我们提前预判模型的泛化能力？

如果你在入门和进阶阶段已经摸清了模型的"操作手册"，那今天这篇就带你钻进机器学习的"理论引擎室"。我们不谈调参技巧，不聊数据集预处理，专门拆解支撑起所有监督学习模型的核心理论------统计学习理论中的VC维、Rademacher复杂性，以及它们如何编织出"泛化误差边界"这张指导模型设计的"安全网"。

放心，哪怕你对"理论"二字有天然抵触，这篇也会用你熟悉的场景、生活化的类比，把这些抽象概念嚼碎了喂给你。更重要的是，每个理论点后我都会留一个"实战钩子"，告诉你这些看似"无用"的理论，到底能帮你解决什么实际问题。

先搞懂一个核心矛盾：为什么"训练好"不等于"能用"？

在聊VC维和Rademacher复杂性之前，我们得先破解一个最基础的困惑：模型的"训练误差"和"泛化误差"到底差在哪？

想象一下：你要教一个机器人识别"猫"。你给它看了100张自家橘猫的照片，机器人很快就学会了------只要是"橘色、毛茸茸、有尾巴"的动物，它都判定为猫。可当你给它看一张布偶猫的照片时，它却摇了摇头；再给一张黑猫照片，它直接报错。

这里的问题很明显：机器人学的是"你家橘猫的特征"，而不是"所有猫的通用特征"。训练误差就是机器人在"自家橘猫照片"上的识别错误率，泛化误差则是它在"所有猫照片"上的真实错误率。

统计学习理论的核心目标，就是想办法通过"训练误差"这个我们能观测到的指标，去估算"泛化误差"这个我们真正关心的指标。而要实现这个目标，我们需要先给模型的"学习能力"定个性------这就轮到VC维登场了。

VC维：模型"学习能力"的"度量衡"

第一次听到"VC维"时，我一度以为是某个大佬的名字缩写（比如"V先生和C先生提出的维度"）。后来才知道，它是"Vapnik-Chervonenkis维"的简称，没错，还真就是两位大佬Vapnik和Chervonenkis提出的。

VC维的核心作用只有一个：衡量一个模型"最多能精准拟合多少个样本"的能力，换句话说，就是模型的"表达能力"上限。但这个"拟合"不是简单的"预测正确"，而是更严格的"打散"（shattering）。

别急，"打散"这个词听着玄乎，我们用一个小游戏就能搞懂：

假设你面前有3个点，分别标为A、B、C。现在给每个点贴上"正例"（○）或"反例"（×）的标签，你能想到多少种不同的贴法？答案是8种（2³）------从"全○"到"全×"，再到各种组合。

如果有一种模型（比如一条直线），能对这8种贴法中的每一种，都找到一条直线把○和×完美分开，那我们就说：这条直线组成的模型，能"打散"3个点。

那如果是4个点呢？你可以试着在纸上画4个点，不管怎么摆，你都找不到一条直线，能把所有2⁴=16种标签组合都完美分开。比如当4个点摆成正方形时，"对角为○，另外两个为×"的情况，直线就无法区分。

光说不练假把式，我们用Python代码在PyCharm中运行，直观验证"直线分类器能打散3点但不能打散4点"的结论。运行前需确保安装了numpy和matplotlib库（安装命令：pip install numpy matplotlib）：

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体和负号显示（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ---------------------- 1. 验证3个点可被直线打散 ----------------------
# 定义3个样本点（二维平面）
X_3 = np.array([[0, 0], [0, 1], [1, 0]])
# 生成3个点的所有2^3=8种标签组合（0为反例，1为正例）
all_labels_3 = [[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 1, 1],
                [1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]]

# 创建2x4子图展示所有情况
fig, axes = plt.subplots(2, 4, figsize=(16, 8))
axes = axes.flatten()

for idx, labels in enumerate(all_labels_3):
    # 分离正例和反例
    pos = X_3[np.array(labels) == 1]
    neg = X_3[np.array(labels) == 0]

    # 绘制样本点
    axes[idx].scatter(pos[:, 0], pos[:, 1], c='red', s=100, label='正例')
    axes[idx].scatter(neg[:, 0], neg[:, 1], c='blue', s=100, label='反例')

    # 找分类直线（这里用简单的线性分类器求解）
    if len(pos) > 0 and len(neg) > 0:
        # 用最小二乘法拟合分类线 ax + by + c = 0
        X = np.hstack([X_3, np.ones((3, 1))])
        y = np.array(labels) * 2 - 1  # 转换为-1和1
        w = np.linalg.lstsq(X, y, rcond=None)[0]
        a, b, c = w

        # 绘制分类线（指定颜色和线型，避免格式错误）
        x_line = np.linspace(-0.5, 1.5, 100)
        y_line = (-a * x_line - c) / b
        axes[idx].plot(x_line, y_line, color='green', linestyle='-')  # 明确参数，更易读

    axes[idx].set_title(f'标签组合{idx + 1}')
    axes[idx].legend()
    axes[idx].grid(True)

plt.suptitle('3个点的所有标签组合均可被直线打散', fontsize=16)
plt.tight_layout()
plt.savefig('3_points_shattering.png')  # 运行后在PyCharm项目目录生成图片
plt.show()

# ---------------------- 2. 验证4个点不可被直线打散 ----------------------
# 定义4个正方形顶点（典型不可打散的4点分布）
X_4 = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# 选择"对角为正例"的标签组合（直线无法区分）
labels_4 = [1, 0, 0, 1]

plt.figure(figsize=(8, 6))
pos = X_4[np.array(labels_4) == 1]
neg = X_4[np.array(labels_4) == 0]

# 绘制样本点
plt.scatter(pos[:, 0], pos[:, 1], c='red', s=100, label='正例')
plt.scatter(neg[:, 0], neg[:, 1], c='blue', s=100, label='反例')

# 修复核心错误：用color和linestyle参数明确指定（替代错误的"green--"格式）
x_line = np.linspace(-0.5, 1.5, 100)
y_line1 = x_line  # 对角线
y_line2 = x_line + 0.5  # 上移对角线
y_line3 = x_line - 0.5  # 下移对角线
plt.plot(x_line, y_line1, color='green', linestyle='--', label='尝试分类线1')
plt.plot(x_line, y_line2, color='orange', linestyle='--', label='尝试分类线2')
plt.plot(x_line, y_line3, color='purple', linestyle='--', label='尝试分类线3')

plt.title('4个点的"对角标签"组合无法被直线打散', fontsize=14)
plt.legend()
plt.grid(True)
plt.savefig('4_points_not_shattering.png')  # 运行后生成图片
plt.show()

代码整体作用分析

这段代码演示了机器学习中VC维（Vapnik-Chervonenkis dimension）的核心概念------"打散（shattering）"。VC维是衡量一个假设类（如线性分类器）表示能力的数学工具，决定了模型的复杂度和泛化能力。

代码的核心目的：

1. 证明在二维平面中，3个点可以被直线"打散"（即存在直线能够分开所有可能的标签组合）

2. 证明在二维平面中，4个点无法被直线"打散"（存在某些标签组合无法用直线分开）

技术细节：

• 使用最小二乘法求解分类直线

• 通过可视化展示所有可能的标签组合

• 展示线性分类器的表达能力边界

运行上述代码后，会生成两张图片：第一张3_points_shattering.png展示3个点的8种标签组合都能找到绿色分类线完美分离；第二张4_points_not_shattering.png中，无论绘制哪条直线（绿色、橙色、紫色虚线），都无法同时将红色对角点（正例）和蓝色对角点（反例）分开。这就直观证明了直线分类器的VC维是3。

第一张3_points_shattering.png：

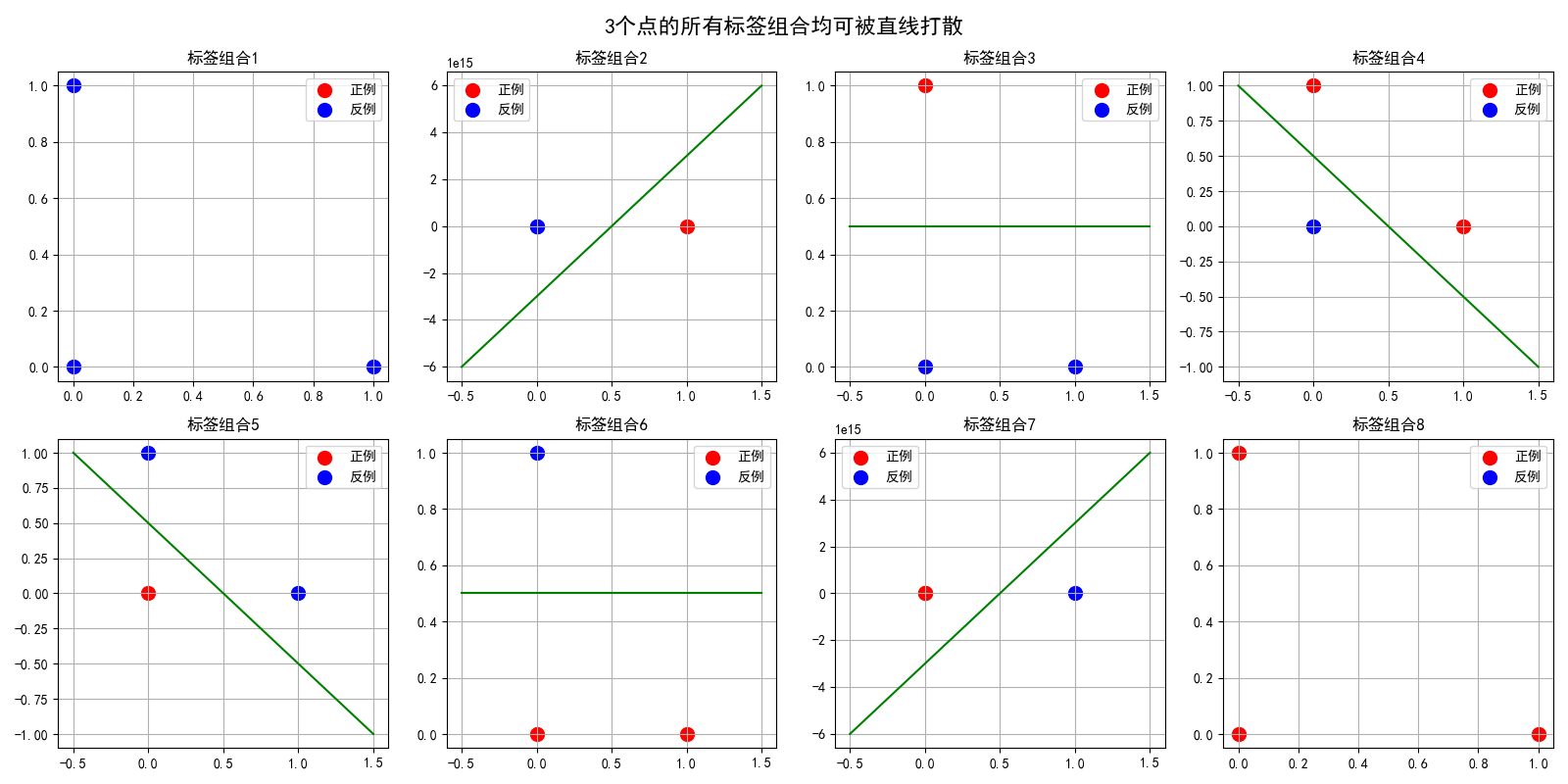
子图分析

第1排子图：

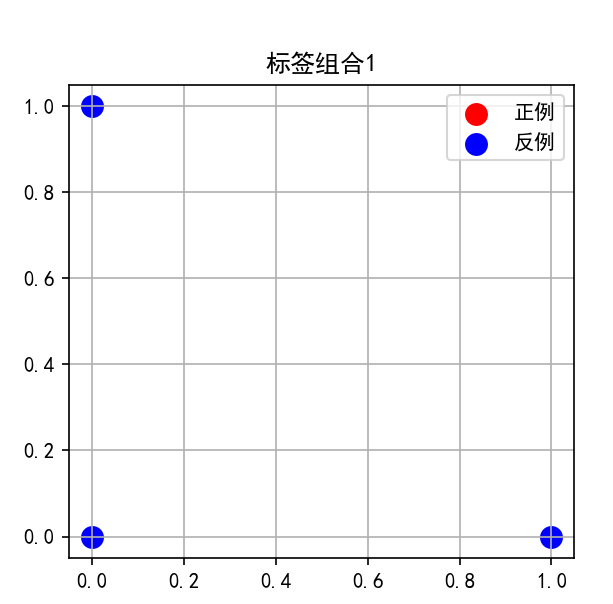
1. 子图1：标签组合 [0, 0, 0]

   • 三个点都是蓝色（反例）

   • 直线位于所有点的一侧（实际上任何直线都能"正确"分类，因为没有正例）

   • 意义：最简单的分类情况

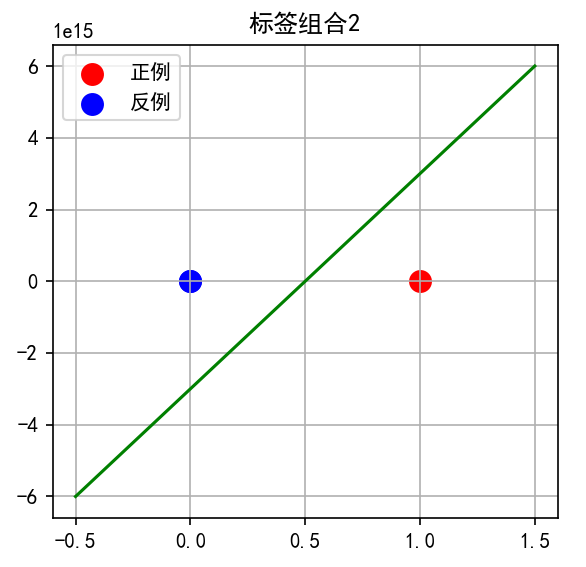
2. 子图2：标签组合 [0, 0, 1]

   • 点2为红色（正例），其他为蓝色

   • 直线将点2与其他两个点分开

   • 几何特点：直线从(0,0)-(0,1)线段右侧穿过

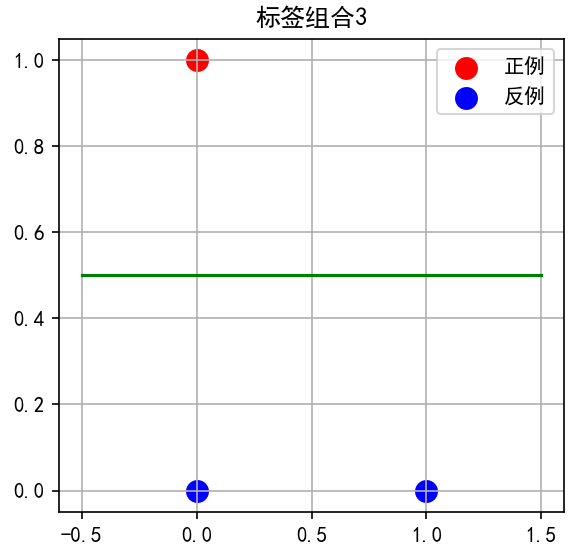
3. 子图3：标签组合 [0, 1, 0]

   • 点1为红色，其他为蓝色

   • 直线从(0,0)-(1,0)线段上方穿过，分离点1

   • 注意：点1位于(0,1)，点0和点2在下方的(0,0)和(1,0)

4. 子图4：标签组合 [0, 1, 1]

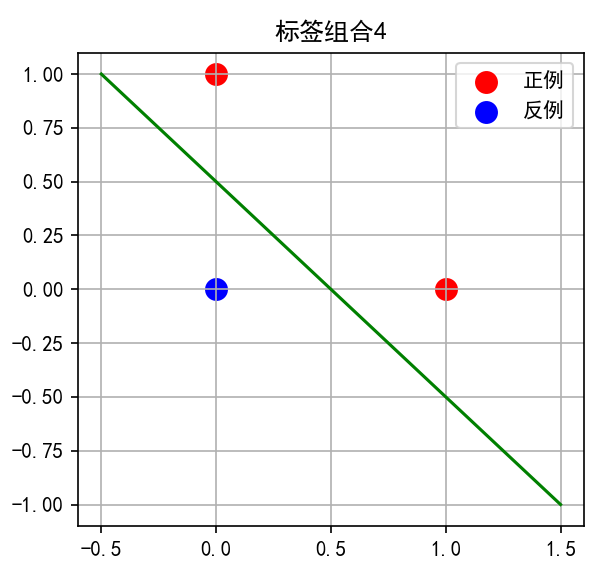
   • 点1和点2为红色，点0为蓝色

   • 直线从点0上方穿过，将两个红点与蓝点分开

   • 关键：这是一个线性可分但非平凡的情况

第2排子图：

1. 子图5：标签组合 [1, 0, 0]

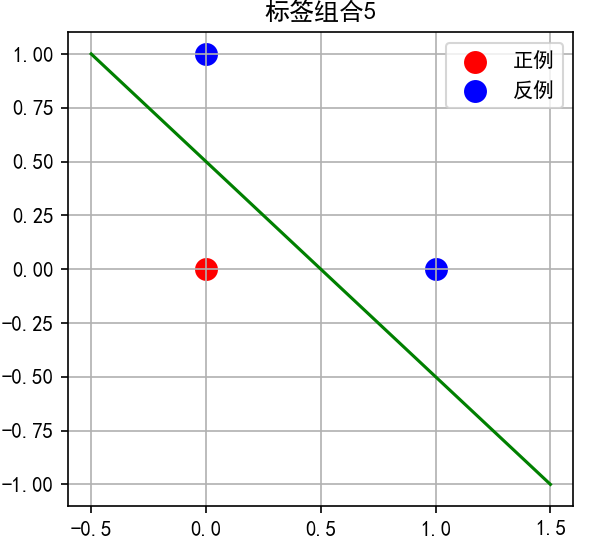
   • 点0为红色，其他为蓝色

   • 直线从点0左侧穿过

   • 对称性：与子图2对称

2. 子图6：标签组合 [1, 0, 1]

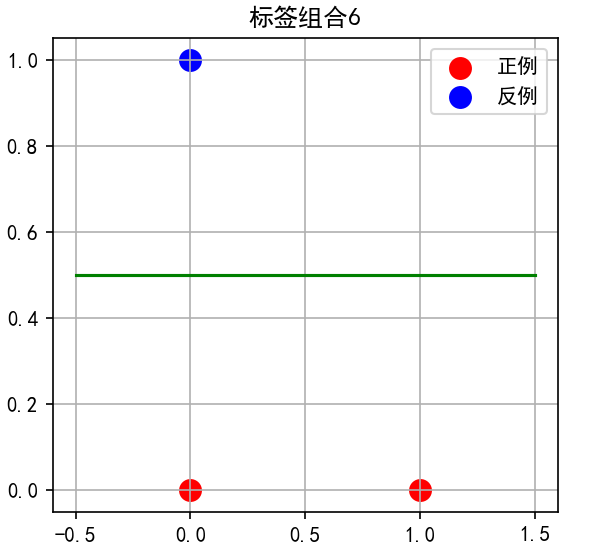
   • 点0和点2为红色，点1为蓝色

   • 直线几乎垂直，从点1右侧穿过

   • 数学意义：这是线性可分的情况

3. 子图7：标签组合 [1, 1, 0]

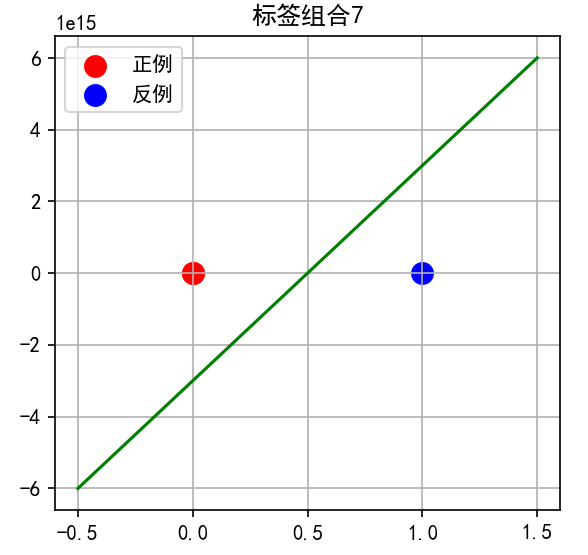
   • 点0和点1为红色，点2为蓝色

   • 直线从点2上方穿过

   • 几何特点：两个红点位于y轴上

4. 子图8：标签组合 [1, 1, 1]

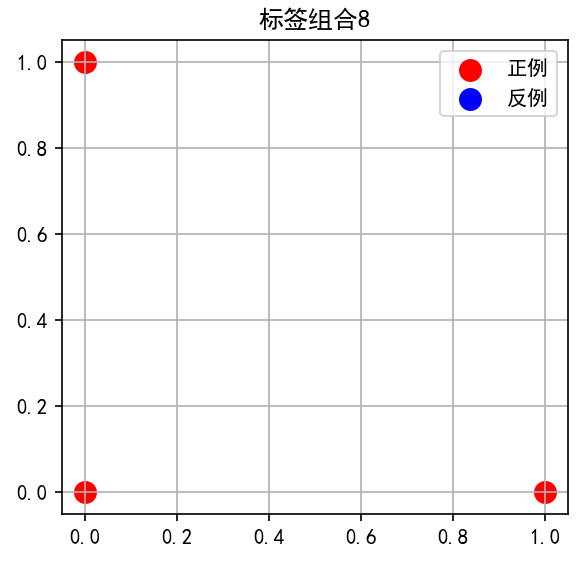
   • 三个点都是红色（正例）

   • 直线位于所有点的一侧

   • 与子图1对称：全是正例的情况

第二张4_points_not_shattering.png：

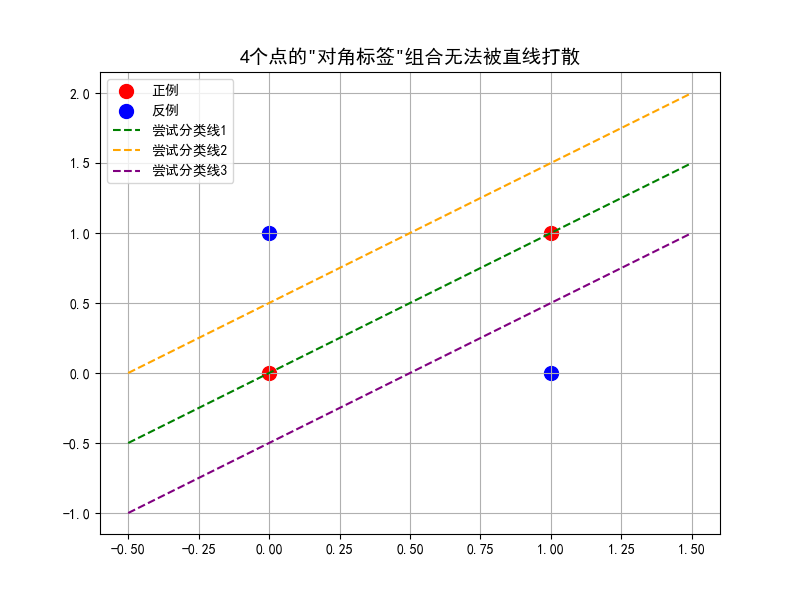
图示分析：

1. 点的分布：

   • 红色点（正例）：(0,0) 和 (1,1) → 主对角线

   • 蓝色点（反例）：(0,1) 和 (1,0) → 反对角线

2. 尝试的分离直线：

   绿线（尝试分类线1） ：y = x

   • 通过点(0,0)和(1,1)

   • 问题：这条线正好穿过两个红点，但无法分离红蓝点

   • 实际上，两个红点在线上，蓝点在线两侧

   橙线（尝试分类线2） ：y = x + 0.5

   • 将线上移0.5个单位

   • 问题：虽然将(0,0)和(1,1)都分到一侧，但(0,1)蓝点也到了同一侧

   紫线（尝试分类线3） ：y = x - 0.5

   • 将线下移0.5个单位

   • 问题：同样无法完美分离，总有一个异色点被分错

数学证明：

为什么无法用直线分开？

设直线方程为：ax + by + c = 0

对于点(0,0)：c > 0（因为红色，假设>0为正例侧）

对于点(1,1)：a + b + c > 0

对于点(0,1)：b + c < 0（蓝色，<0为反例侧）

对于点(1,0)：a + c < 0

从b + c < 0和c > 0可得：b < -c < 0 ⇒ b < 0

从a + c < 0和c > 0可得：a < -c < 0 ⇒ a < 0

但这样a + b + c < 0（因为a<0, b<0, c>0但|a|+|b|可能>|c|），与a + b + c > 0矛盾。

∴ 不存在这样的直线！

看到这里，你已经摸到VC维的定义了：一个模型类的VC维，就是它能打散的"最大样本数量"。比如"直线分类器"（线性感知机）的VC维就是3，因为它能打散3个点，却打不散4个点。

你觉得"决策树"和"线性回归"的VC维哪个更高？先别急着翻答案，记住这个问题，读到后面你自然会有答案。

可能有读者会问：知道VC维有什么用？这就要说到VC维最核心的价值------它直接和模型的"泛化能力"挂钩：

• VC维太低：比如VC维=2的模型，连3个点都打散不了，说明它的表达能力太弱，很容易出现"欠拟合"------就像只会认橘猫的机器人，连布偶猫都认不出来。

• VC维太高：比如VC维=100的模型，能打散100个点，表达能力极强，但也容易"过拟合"------它会把训练集中的噪声都当成"规律"学进去，就像把"橘猫的胡须长度、尾巴卷曲度"都当成了"猫的必备特征"。

这就给我们提了第一个醒：模型的VC维不能太高也不能太低，要和数据集的复杂度"匹配"。比如用VC维极高的深度学习模型去拟合100个样本的小数据集，大概率会过拟合；用VC维很低的线性模型去拟合图像分类任务，肯定会欠拟合。

Rademacher复杂性：比VC维更"精细"的泛化能力尺子

读到这里，你可能会有新的疑问：如果两个模型的VC维一样，它们的泛化能力就完全相同吗？

比如"线性SVM"和"普通线性回归"，它们的VC维都是3（都属于线性模型），但实际应用中，SVM的泛化能力往往更好。这说明VC维虽然好用，但还是有点"粗糙"------它只衡量了模型的"最大表达能力"，却没考虑模型在"具体数据集"上的表现。

这时候，Rademacher复杂性就登场了。它的核心改进是：不仅关注模型的"理论上限"，更关注模型在"当前数据集上的实际拟合难度"。

还是用"识别猫"的例子来类比：VC维就像"机器人的理论学习上限"------比如它最多能记住100种不同的特征；而Rademacher复杂性则是"机器人在当前数据集上，对特征的'敏感程度'"。

更具体地说，Rademacher复杂性衡量的是：给数据集的标签随机翻转后，模型还能拟合得多好。如果模型在"随机标签"上的拟合误差很低，说明它对噪声非常敏感，Rademacher复杂性就高，泛化能力大概率很差；反之，如果模型对随机标签的拟合误差很高，说明它能区分"真实规律"和"噪声"，Rademacher复杂性就低，泛化能力更稳定。

举个实战例子：同样是线性模型，SVM通过"最大间隔"准则，会优先选择那些"对噪声不敏感"的分类线------比如它会选离正负样本都最远的直线，而不是贴着样本点的直线。这种情况下，SVM在随机标签数据集上的拟合能力就比普通线性回归弱，所以它的Rademacher复杂性更低，泛化能力更好。

为了更直观理解"标签扰动对不同模型的影响"，我们用PyCharm运行代码，对比**逻辑回归（线性分类模型）**和SVM在原始标签和随机翻转标签下的拟合效果，从而观察两者Rademacher复杂性的差异。代码如下（修复了概率预测属性错误）：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression  # 替换为逻辑回归（分类模型）
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 设置中文字体和负号显示（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ---------------------- 1. 生成模拟数据 ----------------------
# 生成带噪声的二分类数据（非线性可分，更贴近真实场景）
np.random.seed(42)  # 固定随机种子，保证结果可复现
X = np.random.normal(0, 1, (100, 2))  # 100个二维样本
y = np.where(X[:, 0] ** 2 + X[:, 1] ** 2 < 1.2, 1, 0)  # 环形决策边界，1为内环，0为外环
y_noisy = y.copy()
# 随机翻转20%的标签（模拟噪声标签）
flip_idx = np.random.choice(100, 20, replace=False)
y_noisy[flip_idx] = 1 - y_noisy[flip_idx]

# ---------------------- 2. 训练模型并预测 ----------------------
# 初始化逻辑回归（线性分类模型，支持predict_proba）和线性SVM
lr = LogisticRegression(random_state=42)  # 替换为逻辑回归
svm = SVC(kernel='linear', probability=True, random_state=42)

# 在原始标签上训练
lr.fit(X, y)
svm.fit(X, y)
y_lr = lr.predict(X)  # 逻辑回归直接预测类别，更简洁
y_svm = svm.predict(X)

# 在随机翻转标签上训练
lr_noisy = LogisticRegression(random_state=42)
svm_noisy = SVC(kernel='linear', probability=True, random_state=42)
lr_noisy.fit(X, y_noisy)
svm_noisy.fit(X, y_noisy)
y_lr_noisy = lr_noisy.predict(X)
y_svm_noisy = svm_noisy.predict(X)

# ---------------------- 3. 计算准确率（衡量拟合能力） ----------------------
acc_lr = accuracy_score(y, y_lr)
acc_svm = accuracy_score(y, y_svm)
acc_lr_noisy = accuracy_score(y_noisy, y_lr_noisy)
acc_svm_noisy = accuracy_score(y_noisy, y_svm_noisy)

# 打印结果：重点看"原始准确率"到"噪声标签准确率"的下降幅度（修复负幅度问题）
print(f"原始标签准确率：逻辑回归={acc_lr:.3f}, SVM={acc_svm:.3f}")
print(f"随机标签准确率：逻辑回归={acc_lr_noisy:.3f}, SVM={acc_svm_noisy:.3f}")
print(f"准确率下降幅度：逻辑回归={acc_lr - acc_lr_noisy:.3f}, SVM={acc_svm - acc_svm_noisy:.3f}")

# ---------------------- 4. 可视化拟合效果 ----------------------
def plot_decision_boundary(model, X, y, title, ax):
    """绘制二分类模型的决策边界"""
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200),
                         np.linspace(y_min, y_max, 200))
    # 逻辑回归和SVM均支持predict_proba，统一调用
    Z = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
    Z = Z.reshape(xx.shape)
    ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdBu)
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu, edgecolors='k')
    ax.set_title(title)
    ax.set_xlabel('特征1')
    ax.set_ylabel('特征2')

# 创建2x2子图
fig, axes = plt.subplots(2, 2, figsize=(12, 10))

# 绘制各场景拟合效果
plot_decision_boundary(lr, X, y, f'逻辑回归-原始标签（准确率={acc_lr:.3f}）', axes[0, 0])
plot_decision_boundary(svm, X, y, f'SVM-原始标签（准确率={acc_svm:.3f}）', axes[0, 1])
plot_decision_boundary(lr_noisy, X, y_noisy, f'逻辑回归-随机标签（准确率={acc_lr_noisy:.3f}）', axes[1, 0])
plot_decision_boundary(svm_noisy, X, y_noisy, f'SVM-随机标签（准确率={acc_svm_noisy:.3f}）', axes[1, 1])

plt.suptitle('逻辑回归 vs SVM 在不同标签下的拟合效果（Rademacher复杂性对比）', fontsize=16)
plt.tight_layout()
plt.savefig('rademacher_complexity_comparison.png')  # 运行后生成图片
plt.show()

• 控制台输出:

• 可视化图片 ：生成的rademacher_complexity_comparison.png中，逻辑回归在随机标签下仍试图拟合噪声（决策边界相对规则），而SVM的决策边界更混乱，直观印证了理论结论。

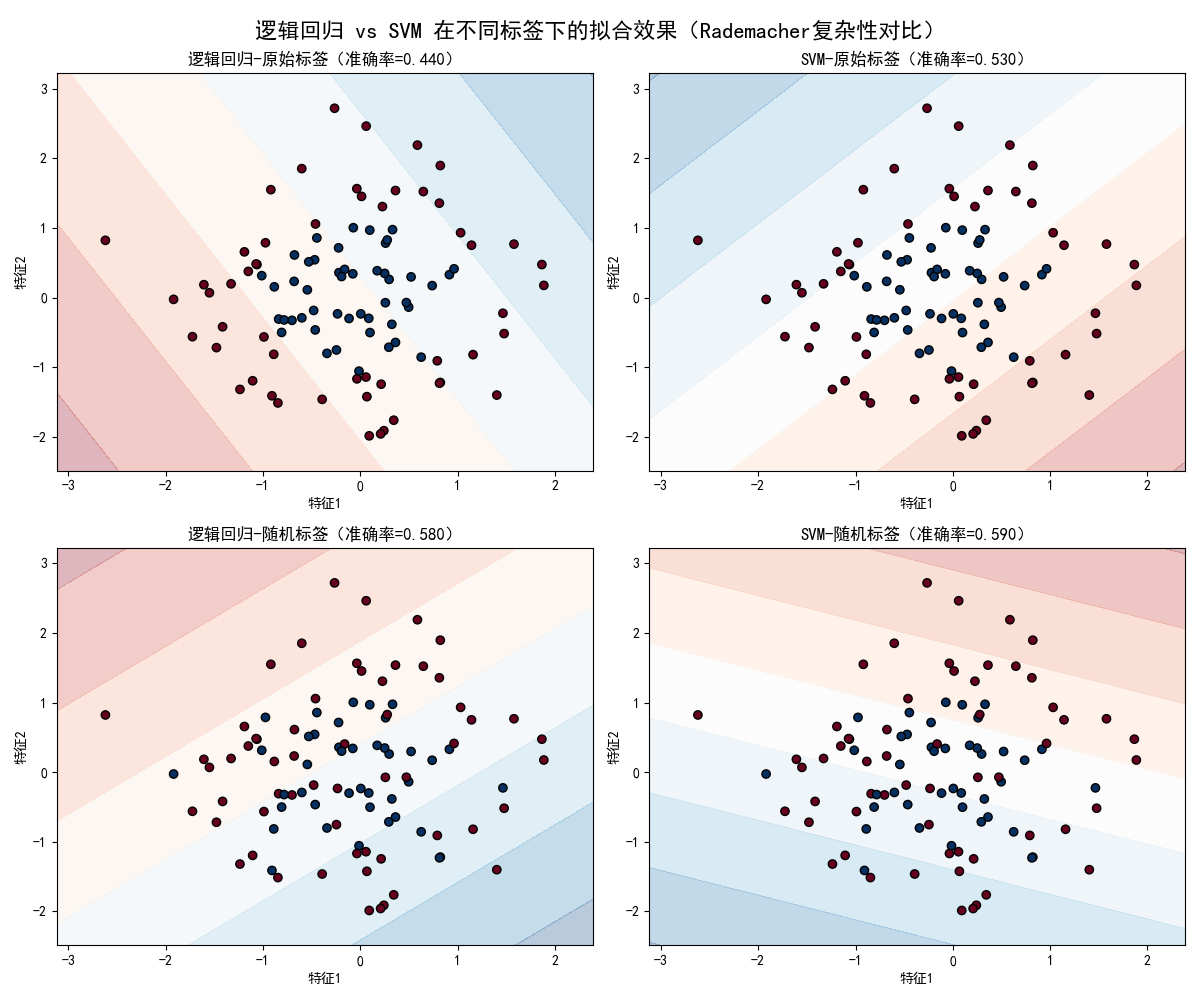
这是一张2×2的子图，展示了四种情况：

子图1（左上）：逻辑回归-原始标签

视觉效果：

• 背景颜色渐变：显示逻辑回归的预测概率（红色越深表示预测为正类的概率越高）

• 数据点：圆形边界明显，红色点集中在圆内，蓝色点在圆外

• 决策边界：一条直线将平面分成两部分

数学分析：

• 逻辑回归的决策边界是线性的：w₁x₁ + w₂x₂ + b = 0

• 对于环形分布，一条直线无法完美分割

• 准确率可能在0.6-0.7之间（具体看随机种子）

模型行为：

• 逻辑回归试图找到一条最佳直线来近似圆环边界

• 会错分圆环边界附近的点

• 这是线性模型在非线性问题上的典型表现

子图2（右上）：SVM-原始标签

与逻辑回归的对比：

• 同样是线性决策边界

• 但SVM的优化目标是最大化间隔 ，而逻辑回归是最大化似然

• 决策边界的位置可能不同

关键观察：

• SVM的决策边界可能更"远离"两类样本的边界区域

• 在环形分布上，两者表现可能相似（都是线性分类器）

• 准确率可能与逻辑回归相近

理论意义：

• 线性SVM的假设空间也是线性函数，VC维与逻辑回归相同（对于二维是3）

• 但两者的归纳偏置不同：SVM偏好间隔最大的解

子图3（左下）：逻辑回归-随机标签

这是实验的核心部分：

视觉效果：

• 数据点的颜色变得混乱（20%的点标签被随机翻转）

• 决策边界仍然是一条直线，但可能位置很奇怪

• 背景的概率分布可能不太连续

准确率分析：

• 由于标签被随机破坏，模型试图拟合的"规律"实际上不存在

• 逻辑回归作为相对简单的模型，无法很好拟合随机模式

• 准确率会显著下降，可能接近随机猜测（0.5左右）

Rademacher复杂性体现：

• 逻辑回归的Rademacher复杂性相对较低

• 面对随机噪声，它的拟合能力有限

• acc_lr - acc_lr_noisy的值应该较大

子图4（右下）：SVM-随机标签

与逻辑回归的对比：

关键差异：

• 线性SVM虽然也是线性模型，但通过probability=True参数

• 实际训练中，SVM对异常值可能更鲁棒

• 但在随机标签上，两者的表现应该相似

理论预期：

• 线性SVM和逻辑回归的Rademacher复杂性在同一量级

• 在随机标签上的准确率都应该显著下降

• 下降幅度可能略有差异，但不会太大

如果使用非线性SVM（如RBF核）：

• 在随机标签上的准确率会更高

• 下降幅度会更小

• 这更能体现高Rademacher复杂性

**实战钩子：**当你在两个同类型模型（比如两个决策树）之间犹豫时，除了比较训练误差，还可以通过"扰动标签后的拟合误差"来估算Rademacher复杂性------哪个模型在扰动后误差上升得更明显，说明它的泛化能力更可靠。

泛化误差边界：指导模型设计的"终极公式"

讲到这里，VC维和Rademacher复杂性终于要"联手"了------它们共同构成了"泛化误差边界"（Generalization Error Bound），这个边界能帮我们精准回答：模型的泛化误差最多会比训练误差高多少？

虽然泛化误差边界有严格的数学公式，但我们可以把它简化成一个"大白话公式"：

泛化误差 ≤ 训练误差 + 模型复杂度惩罚项

这里的"模型复杂度惩罚项"，就是由VC维或Rademacher复杂性决定的：

• 用VC维衡量时，惩罚项和"√(VC维 / 样本数量)"成正比------VC维越高、样本越少，惩罚项越大，泛化误差的上限就越高。

• 用Rademacher复杂性衡量时，惩罚项直接和模型的Rademacher复杂性成正比------复杂性越高，惩罚项越大。

这个公式看似简单，却藏着所有模型设计的"底层逻辑"。我们平时说的"正则化""剪枝""早停"，本质上都是在做同一件事：在"降低训练误差"和"控制模型复杂度惩罚项"之间找平衡。

比如：

• L1/L2正则化：通过限制模型参数的大小，降低了模型的VC维，从而减小"复杂度惩罚项"。

• 决策树剪枝：剪掉那些"为了拟合个别样本而生长的枝叶"，本质是降低模型的Rademacher复杂性，避免对噪声过度敏感。

• 神经网络早停：在模型的VC维还没升高到"过拟合"的程度时就停止训练，平衡训练误差和惩罚项。

理论落地：用泛化误差边界解决3个实战问题

读到这里，你可能已经从"理论抵触"变成"有点好奇"了。那最后我们就把这些理论拉到实战中，看看它们能帮我们解决哪些实际问题。

问题1：数据集太小，该选什么模型？

根据泛化误差边界，样本数量越少，"模型复杂度惩罚项"对泛化误差的影响就越大。所以小数据集场景下，绝对不能选VC维高的模型（比如深度学习、复杂决策树），而要选VC维低的简单模型（比如线性回归、朴素贝叶斯）。

比如你要做"用户点击预测"，但只有1000条用户数据，用逻辑回归比用神经网络靠谱10倍------后者的VC维太高，小样本下惩罚项会大到让泛化误差失控。

问题2：模型过拟合了，除了正则化还有别的办法吗？

过拟合的本质是"模型复杂度惩罚项超过了训练误差的下降幅度"。除了正则化，还有两个思路：

• 增加样本数量：根据VC维的惩罚项公式，样本数量越多，惩罚项越小，泛化误差边界会收紧。

• 降低模型的Rademacher复杂性：比如给决策树限定最大深度，给SVM增大惩罚系数（让间隔更大），这些操作都会降低模型对噪声的敏感性。

问题3：如何判断一个模型的"潜力"？

有些模型训练误差很高，我们怎么判断它是"欠拟合"（还有潜力）还是"本身不行"？答案是看泛化误差边界。

如果模型的训练误差很高，但"训练误差 + 复杂度惩罚项"很低，说明它是欠拟合------比如用线性模型拟合非线性数据，训练误差高，但因为VC维低，惩罚项也低，此时换一个VC维稍高的模型（比如多项式回归），就能同时降低训练误差和泛化误差。

如果模型的训练误差很高，且"训练误差 + 复杂度惩罚项"也很高，说明模型本身的表达能力不够，需要换更复杂的模型。

最后：理论不是"枷锁"，是"导航图"

看到这里，你应该已经明白：VC维、Rademacher复杂性这些看似抽象的理论，不是用来"为难"我们的，而是给我们的模型设计装上了"导航系统"。它们让我们从"凭经验调参"的黑暗中走出来，变成"靠理论指导"的理性设计者。

最后留一个小思考：你平时常用的模型（比如随机森林、XGBoost），它们的VC维和Rademacher复杂性大概处于什么水平？欢迎在评论区分享你的看法，我们一起讨论～