【每日算法】LeetCode148. 排序链表

对前端开发者而言，学习算法绝非为了"炫技"。它是你从"页面构建者"迈向"复杂系统设计者"的关键阶梯。它将你的编码能力从"实现功能"提升到"设计优雅、高效解决方案"的层面。从现在开始，每天投入一小段时间，结合前端场景去理解和练习，你将会感受到自身技术视野和问题解决能力的质的飞跃。

------ 算法：资深前端开发者的进阶引擎

LeetCode 148. 排序链表：分治与指针操作

1. 题目描述

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

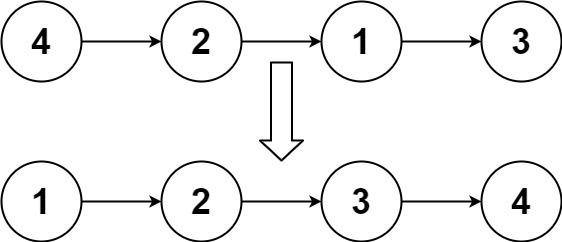
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

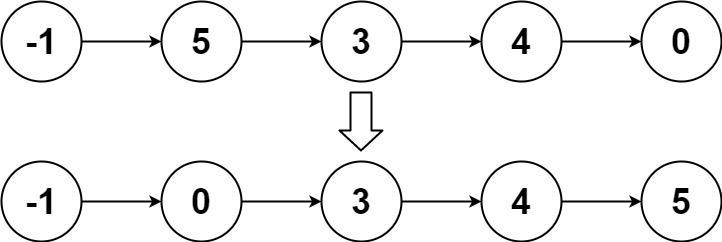
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

进阶要求： 你可以在 O(n log n) 时间复杂度和 常数级空间复杂度 下，对链表进行排序吗？

2. 问题分析

1. 数据结构 ：题目处理的是单链表。与数组不同，链表在内存中非连续，无法像数组一样通过下标在O(1)时间内进行随机访问。这一特性直接影响排序算法的选择。
2. 时间复杂度要求 ：O(n log n)。这提示我们，像冒泡排序、插入排序 等O(n^2)的算法不符合要求。符合此要求的经典算法有：归并排序、快速排序、堆排序。
3. 空间复杂度要求 ：常数级 O(1) 。这是一个关键约束。
   • 递归实现的归并排序 ：递归调用栈的深度为O(log n)，不满足常数空间。
   • 快速排序 ：递归实现同样有O(log n)的栈空间开销。
   • 堆排序：在链路上实现较为复杂。
4. 解决方案 ：为了满足O(n log n)时间和O(1)空间，我们必须采用迭代、自底向上的归并排序。这是本题的最优解，也是考察的核心。

3. 解题思路

3.1 核心思想：自底向上的归并排序 (Bottom-Up Merge Sort)

为什么是归并排序？

归并排序是分治法 的典型应用。对于链表，其合并两个有序链表的操作可以在O(n)时间和O(1)空间内完成（只需要调整指针），这比数组归并需要额外空间更具优势。

如何满足O(1)空间？------ 迭代法

1. 切分 (Split) ：我们不再使用递归来切分链表，而是使用一个变量 subLength 表示当前要归并的子链表长度，初始为1。
2. 合并 (Merge) ：
   • 将链表分成若干段长度为 subLength 的子链表。
   • 将相邻的两个子链表进行合并（这是一个标准的"合并两个有序链表"问题）。
   • 合并完成后，将 subLength 加倍，重复上述过程，直到 subLength 大于或等于整个链表的长度。

关键步骤模拟 ：

假设链表为 [4, 2, 1, 3]

• subLength = 1: 链表视为 [4], [2], [1], [3] -> 两两合并 -> [2,4], [1,3]
• subLength = 2: 链表视为 [2,4], [1,3] -> 两两合并 -> [1,2,3,4]
• subLength = 4: 已排序完成。

3.2 实现细节

1. 虚拟头结点 (dummyHead)：用于简化链表头节点变化的边界情况处理。
2. 切分函数 (cut)：从给定链表头开始，切下指定长度的子链表，并返回剩余部分的头节点。
3. 合并函数 (merge) ：合并两个有序链表，返回新链表的头节点。这是 LeetCode 21. 合并两个有序链表 的直接应用。
4. 主循环 ：外层循环控制 subLength 的增长，内层循环遍历整个链表，进行切分和合并操作。

复杂度分析：

• 时间复杂度：O(n log n) 。外层循环 O(log n) 次，内层循环每次遍历整个链表 O(n)。
• 空间复杂度：O(1)。只使用了固定的几个指针变量。

4. 各思路代码实现 (JavaScript)

4.1 最优解：迭代归并排序 (O(n log n), O(1))

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var sortList = function(head) {
    // 边界条件处理
    if (!head || !head.next) return head;

    // 1. 计算链表总长度
    let length = 0;
    let node = head;
    while (node) {
        length++;
        node = node.next;
    }

    // 2. 创建虚拟头节点，指向原链表
    const dummyHead = new ListNode(0, head);

    // 3. 自底向上归并
    for (let subLength = 1; subLength < length; subLength <<= 1) { // subLength 每次翻倍
        let prev = dummyHead; // prev 用于连接合并好的子链表
        let curr = dummyHead.next; // curr 是当前待处理部分的起点

        while (curr) {
            // 3.1 切分出第一个子链表 head1
            let head1 = curr;
            // 走 subLength - 1 步，找到 head1 的尾部
            for (let i = 1; i < subLength && curr.next; i++) {
                curr = curr.next;
            }

            // 3.2 切分出第二个子链表 head2
            let head2 = curr.next;
            curr.next = null; // 切断 head1 与后面的连接
            curr = head2;
            // 从 head2 开始，再走 subLength - 1 步，找到 head2 的尾部
            for (let i = 1; i < subLength && curr && curr.next; i++) {
                curr = curr.next;
            }

            // 3.3 记录剩余部分，并切断 head2 与后面的连接
            let next = null;
            if (curr) {
                next = curr.next;
                curr.next = null;
            }

            // 3.4 合并 head1 和 head2，并将结果连接到 prev 后面
            const merged = mergeTwoLists(head1, head2);
            prev.next = merged;

            // 3.5 将 prev 移动到合并后链表的末尾，准备连接下一组合并结果
            while (prev.next) {
                prev = prev.next;
            }

            // 3.6 curr 移动到剩余部分，继续处理下一对子链表
            curr = next;
        }
    }

    return dummyHead.next;
};

/**
 * 合并两个有序链表 (LeetCode 21)
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
function mergeTwoLists(l1, l2) {
    const dummy = new ListNode(0);
    let cur = dummy;

    while (l1 && l2) {
        if (l1.val <= l2.val) {
            cur.next = l1;
            l1 = l1.next;
        } else {
            cur.next = l2;
            l2 = l2.next;
        }
        cur = cur.next;
    }

    // 连接剩余部分
    cur.next = l1 ? l1 : l2;
    return dummy.next;
}

4.2 次优解：递归归并排序 (O(n log n), O(log n))

var sortList = function(head) {
    // 递归终止条件
    if (!head || !head.next) return head;

    // 1. 使用快慢指针找到链表中点
    let slow = head, fast = head.next;
    while (fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
    }

    // 2. 切断链表，分成左右两部分
    const mid = slow.next;
    slow.next = null;

    // 3. 递归排序左右两部分
    const left = sortList(head);
    const right = sortList(mid);

    // 4. 合并两个有序链表
    return mergeTwoLists(left, right);
};
// mergeTwoLists 函数同上

4.3 简单解（不符合要求）：转为数组排序 (O(n log n), O(n))

var sortList = function(head) {
    if (!head) return null;
    
    // 1. 链表转数组
    const arr = [];
    let curr = head;
    while (curr) {
        arr.push(curr.val);
        curr = curr.next;
    }
    
    // 2. 数组排序
    arr.sort((a, b) => a - b);
    
    // 3. 数组转回链表
    const dummy = new ListNode(0);
    curr = dummy;
    for (const val of arr) {
        curr.next = new ListNode(val);
        curr = curr.next;
    }
    
    return dummy.next;
};

5. 各实现思路的复杂度、优缺点对比

思路	时间复杂度	空间复杂度	优点	缺点	是否满足进阶要求
迭代归并排序	O(n log n)	O(1)	满足所有进阶要求；纯指针操作，空间效率极致	代码实现相对复杂，边界条件需仔细处理	是
递归归并排序	O(n log n)	O(log n)	代码清晰，易于理解和实现；分治思想的经典体现	递归调用栈消耗额外空间，不满足常数空间要求	否
转为数组排序	O(n log n)	O(n)	实现极其简单，快速；利用语言原生API	需要额外O(n)空间存储数组和新建链表，破坏了原链表节点	否

6. 总结

6.1 技术要点回顾

1. 链表特性 ：无随机访问能力，O(1)时间的插入/删除是其优势。排序算法需要适应这一特性。
2. 归并排序的适应性：对于数据结构，归并排序的合并操作可以非常高效地通过改变指针来实现，无需像数组一样开辟新空间来存储中间结果。
3. 双指针技巧 ：
   • 快慢指针：在递归法中用于高效找到链表中点。
   • 指针操作 ：在迭代法的cut和merge过程中，对指针（next）的精确控制是正确实现的关键，也是前端开发者需要熟练掌握的核心技能之一。
4. 虚拟头节点：一个极其有用的技巧，可以统一处理链表头节点可能发生变化的情况，简化代码逻辑。

6.2 在前端开发中的实际应用场景

虽然前端中直接操作链表排序的场景不多，但本题所锻炼的能力具有广泛的迁移价值：

1. 复杂状态管理 ：在大型前端应用（如使用Vuex、Redux）中，管理一条按时间、优先级排序的操作日志流 或消息列表，其底层优化思想与归并排序类似------将大规模数据分块处理再合并。
2. 高性能列表渲染 ：在实现虚拟滚动 或无限加载 列表时，数据可能是分页/分块到达的。你需要将新到达的有序数据块 与现有的有序列表 进行高效合并并更新DOM，这个过程就是mergeTwoLists的变体。优化此合并过程能极大提升列表滚动的流畅度。
3. 构建工具与数据处理：在编写Webpack插件、Babel插件或进行Node.js流式数据处理时，经常会遇到需要将多个有序序列（如源映射片段、日志事件）合并成一个有序序列的场景。
4. 思维模式提升 ：分治思想是解决复杂问题的利器。无论是前端的组件设计（将大组件拆分为可复用的小组件）、性能优化（将长任务分解为多个微任务），还是工程化中的任务拆分，其核心逻辑与归并排序一脉相承。