目录
[1. 非线性放大电路:负责 "起振 + 稳幅"](#1. 非线性放大电路:负责 “起振 + 稳幅”)
[2. 正反馈网络:负责 "相位平衡"](#2. 正反馈网络:负责 “相位平衡”)
[3. 选频网络:负责 "正弦纯净"](#3. 选频网络:负责 “正弦纯净”)
前面的文章中我们学习了如何让集成运放工作在深度负反馈的条件下,从而获得理想线性的增益效果,但这仅仅只能将已知信号给放大。那如果我现在想要有一个信号发生器呢?即我需要自己做一个能够产生正弦波的电路,以前的负反馈就不再适用了。而正弦振荡器则是实现它的关键。
一、振荡器的条件:"无中生有"的信号从哪来?
先明确核心:正弦波振荡器是 "不需要外部输入,能自己输出固定频率、幅值正弦信号的电路"。
它和自激振荡的区别很关键(这一点我还未深入学习,后续有可能补充自激振荡的文章):
- 自激振荡:负反馈电路里的 "干扰",频率不可控;
- 正弦波振荡器:正反馈 + 选频网络,频率、幅值可控。
要让 "无中生有" 的正弦波稳定持续,必须同时满足这三个条件):
1. 非线性放大电路:负责 "起振 + 稳幅"
放大电路得是非线性的(比如带二极管、三极管的电路):
- 起振时:放大倍数A足够大,让环路增益 |AF| > 1,信号从噪声开始逐渐放大;
- 稳幅时:信号振幅增大到一定程度,非线性元件会 "自动降低放大倍数|A|",最终让 |AF| = 1。
2. 正反馈网络:负责 "相位平衡"
反馈网络必须是正反馈,即反馈信号与输入信号同相,总相移满足φA+φF=2πn,其中n 为整数)。
只有正反馈才能让信号 "循环增强"------ 如果是负反馈,信号会互相抵消,根本振荡不起来。但虽然这里是正反馈,信号也不会无限制的增强,而是会停留在电源电压附近。
3. 选频网络:负责 "正弦纯净"
选频网络(比如 RC 串并联、LC 回路)的作用是只让某一个频率的信号满足相位平衡条件:
- 其他频率的信号要么相移不满足,要么|AF| < 1无法持续;
- 最终只有目标频率的正弦波能 "活下来",保证输出是纯净的正弦信号。
- 选频网络的特点就是选出单独一个频率的信号,而根据傅里叶变换的思想:任何一个信号都可以由正余弦波组成,现在我们反过来只筛出一个频率,即无数个正余弦波中只保留一个频率,就能产生正弦波了。
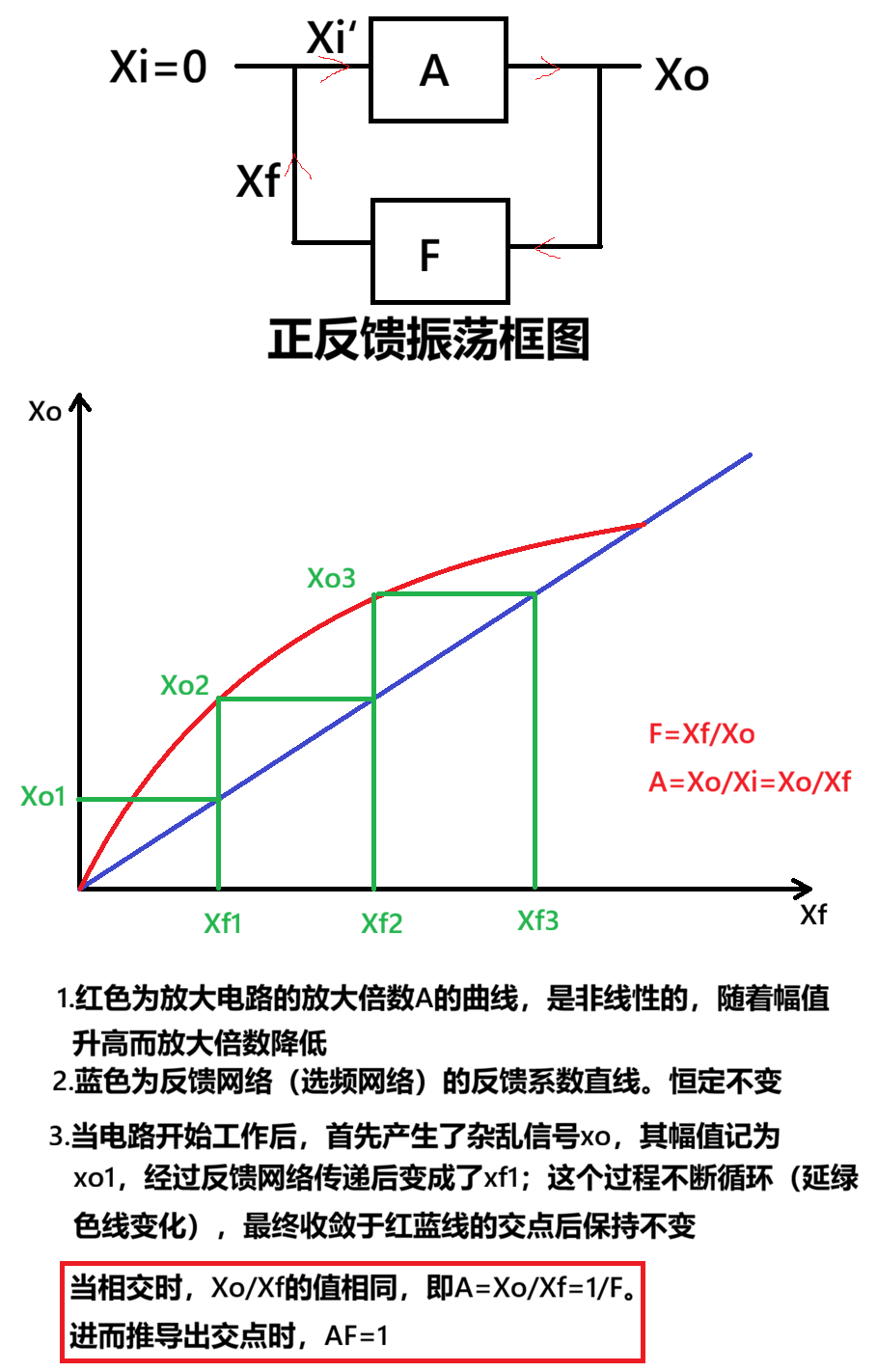
上述推导的是在该网络条件下的幅值保持恒定的条件。即从图中可以看出,最开始AF>1,且这个值逐渐减小,最终在AF=1时收敛保持恒定。同时由于A、F都是相量的形式,所以还隐含了一点:幅角相加等于2nπ。
但是这里只证明了幅值条件,他的形状可以是任意的啊,你怎么能说他是正弦波呢?由傅里叶变换的思想:任何一个信号都可以由正余弦波组成,现在我们反过来只筛出一个频率,即无数个正余弦波中只保留一个频率,就能产生正弦波了。
二、RC选频网络

从这里可以看出,当f=f0时,F反馈系数最大=1/3,且φf=0°
于是这样一个RC选频网络就能选出f0附近频率的信号,注意:这个选频比较温和,选出来的相近的信号,而非只有单独的一个频率。不过这种选频效率已经足够让整体体现正弦波的特点了,只不过可能不够精准,多用于对正弦波波形要求不是很高的场景中。
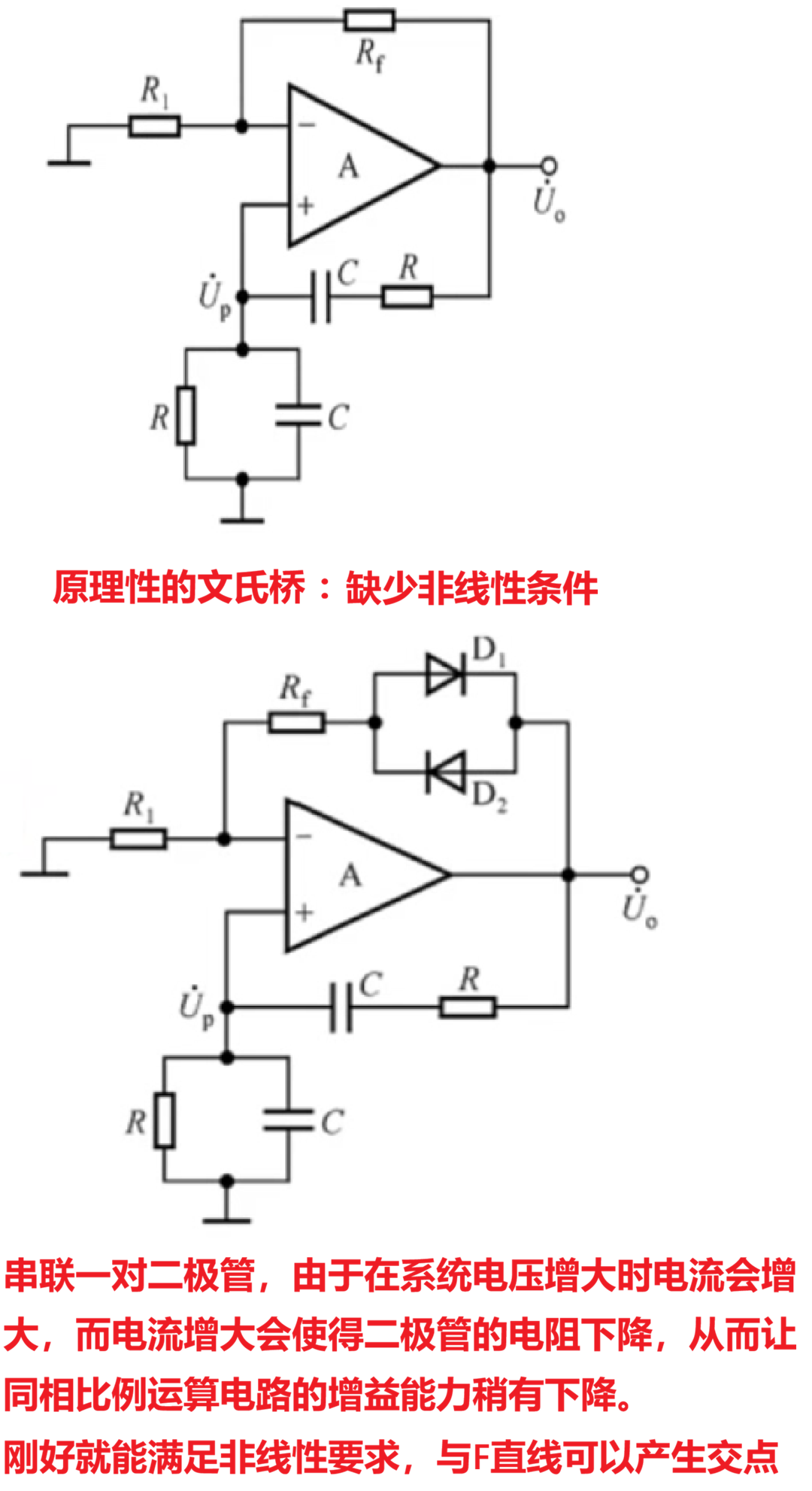
三、RC桥式正弦波振荡电路(文氏桥电路)
在了解了选频网络后,我们就已经掌握了正弦振荡器的精髓了,现在我们加入放大电路将其做成一个完整的振荡器。
(1)什么样子的电路可以满足振荡器的条件?
要让放大电路能支撑振荡器工作,核心要同时满足相位匹配(正反馈)和放大能力达标(起振 + 稳幅)。
(2)文氏桥电路
于是我们将采取集成运放这个组件来做正弦振荡器的放大器,不过由于他的同相比例运算电路的增益是线性的,无法与F的直线产生交点,所以我们会引入一个非线性原件,比如串联一个热敏电阻或者二极管。