电压比较器
开环运放和正反馈运放的传输特性都是一样的,uP大于uN就输出+Vcc,反之输出-Vcc;那为啥还要用正反馈呢?这是因为正反馈能很大的提高从-Vcc到+ Vcc的斜率,也就是信号的Tr和Tf都更大。
阈值UTU_{T}UT :指的是输出发生跳变时的Ui,也就是uP=uN时的Ui
一般使用比较器时,一端会接一个固定电平Vref,另一端接Ui
电压比较器的种类
单限比较器 :只有一个阈值
双限比较器 :有两个阈值,电压从小到大发生两次跃变
滞回比较器 :有两个阈值,且从小到大的阈值不等于从大到小的阈值
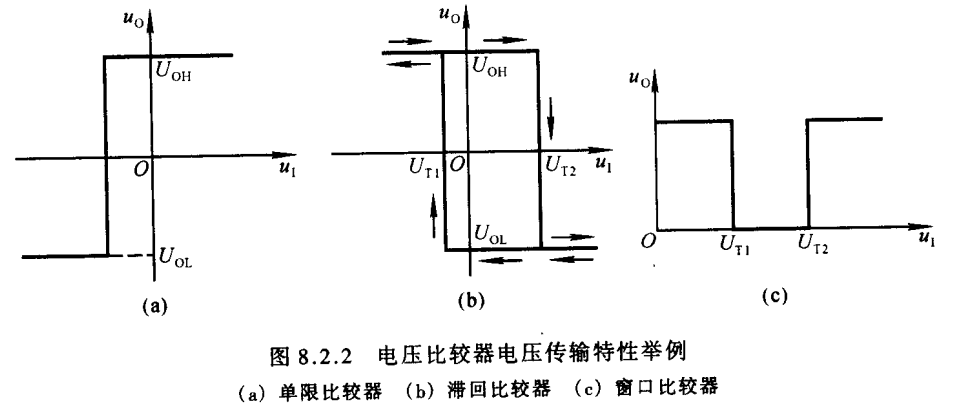
过零电压比较器
为了获得任意输出电压,而不是只能得到供电电压幅值,可以在输出端加限幅电路,具体就是双向稳压管,这样就能依据所选管子的稳压值来获得任意小于供电电压Vcc的输出电压,如图所示。如果选择两个稳压值不同的稳压管则可以得到不同的上限和下限幅值
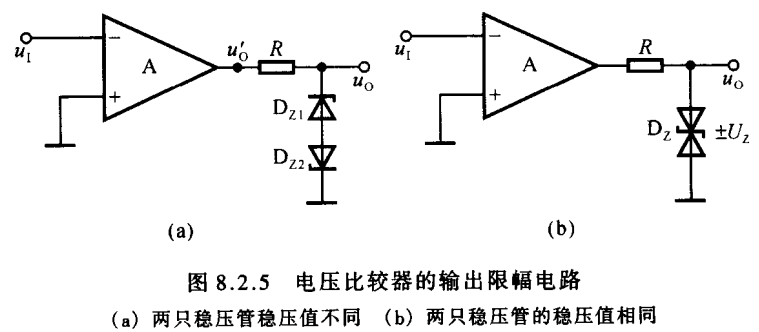
但是如此操作需要加上限流电阻R,由于R的存在提升了比较器输出电阻,所以要求负载RL也要比较大,不然不能保证稳压管两端分压,从而无法保证稳压管导通工作。这相当于提高了负载的要求。
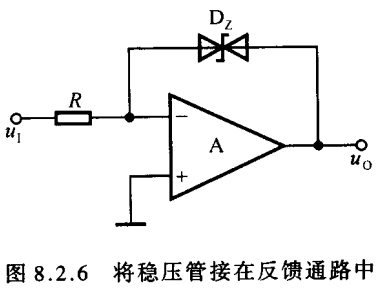
所以想到如下电路(很精妙),将稳压管放到反馈回路中,这样在输出电压不超过稳压值Vz时,运放是比较器,当输出电压Vo超过Vz时,稳压管导通,形成负反馈电路,N端虚短到GND,Vo限制到Vz,稳压管行使稳压功能。
此电路具有以下优势
- 没有了R的引入,不会提高对负载RL的要求
- 只要uI过零,稳压管负反馈电路就启动,使运放只工作在线性区,提高了输出电压的变化速度,因为少了退饱和的过程
- 由于集成运放的净输入电压和净输入电流均近似为零,从而保护了输入级
单限电压比较器
要想使uI的阈值电压UT不等于0,可以有多种实现方法,本质就是使uP=uN时的uI≠0。所以可以在ref端加一个ref电压,也可以在输入端和Vref进行电压叠加。
如果想保持参考端接地,就需要如图操作
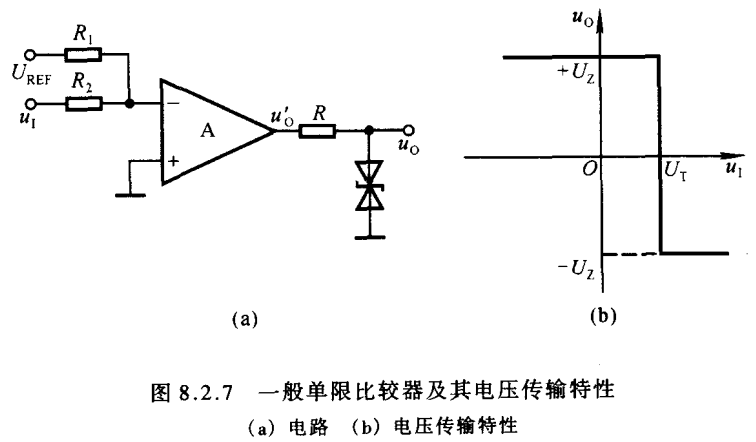
此时N端的电压为(叠加定理)
uN=R2R1+R2UREF+R1R1+R2uI=0UT=−R2R1UREF\begin{align} & u_{N}=\frac{R_{2}}{R_{1}+R_{2}}U_{REF}+\frac{R_{1}}{R_{1}+R_{2}}u_{I}=0 \\ & U_{T}=\textcolor{red}{-}\frac{R_{2}}{R_{1}}U_{REF} \end{align} uN=R1+R2R2UREF+R1+R2R1uI=0UT=−R1R2UREF
这种单限比较器可以用来调制PWM的占空比,比如在使用它对三角波信号进行比较,不同的UT可以输出不同的占空比(这就是一些DCDC芯片调节输出占空比的原理)
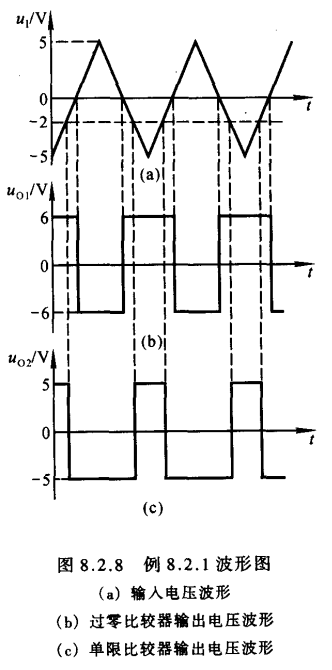
滞回比较器
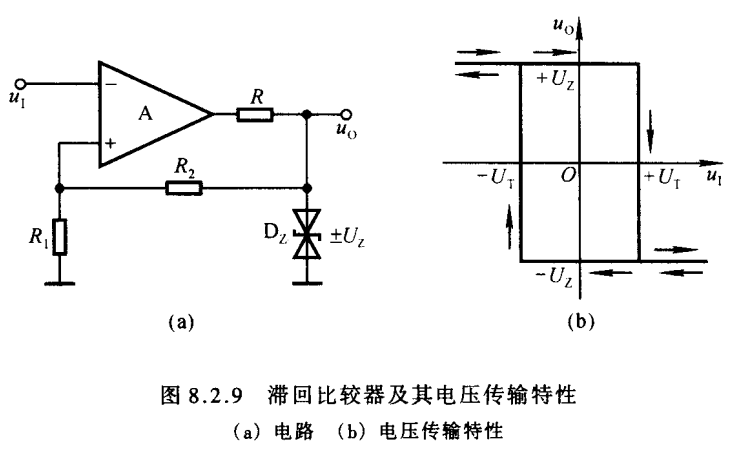
如图8.2.2(b)所示,它的特点是Uo从高变低和从低变高的阈值UT不同,说明Uo的高低会影响到阈值电压UT,而阈值电压和Vref直接相关,所以想到,想要构建滞回电路就需要将输出电压Uo引入到Vref电路中,如图。一种简单的思想就是直接把uo引到ref端,同时ref端取消接地,这种接法也能实现滞回,但是不能调节,UT=Uz
uO=+UZ时,uT1=uN=uP=R1R1+R2UZuO=−UZ时,uT2=uN=uP=−R1R1+R2UZuT1≠uT2 \begin{align} & u_{O}=+U_{Z}时,u_{T_{1}}=u_{N}=u_{P}=\frac{R_{1}}{R_{1}+R_{2}}U_{Z} \\ & u_{O}=-U_{Z}时,u_{T_{2}}=u_{N}=u_{P}=-\frac{R_{1}}{R_{1}+R_{2}}U_{Z} \\ & u_{T_{1}}\neq u_{T_{2}} \end{align} uO=+UZ时,uT1=uN=uP=R1+R2R1UZuO=−UZ时,uT2=uN=uP=−R1+R2R1UZuT1=uT2
所以,达到图b所示效果,且阈值数值相等符号相反;同时可以通过调整R1和R2的阻值来调整阈值电压UT的大小。
这里有个比较好的分析思想可以学习,就是没必要关心前面输入是怎么变化的,直接抓住uo的结果分析就行,反正uo只有两个值。这样分析很直观方便,如果再把uI的状态引进来,分析就复杂了。
可以看出,滞回是个正反馈电路 ,所以它的变化边沿会很陡,变化会很快。
问题 :另外,可能会想,若是第一次上电呢?此时uo什么状态?此时uI和谁比较?
答:由于滞回处于正反馈状态,初始加电时在N,P两端产生的扰动即可使输出uo迅速饱和,但由于扰动的不确定,所以uo的饱和值也不确定,要么+Uz要么-Uz,但一定是饱和的,所以初始uI第一次进行比较时,ref端就已经有比较的值了。
以上的滞回电路的阈值电压UT是Y轴对称的,若是不想这样,想任取UT要如何做?上面是uo通过R1,R2接地,N端取R1的电压,实现效果是对u=0对称,那么将接地换成一个vref,它将对uo=vref对称
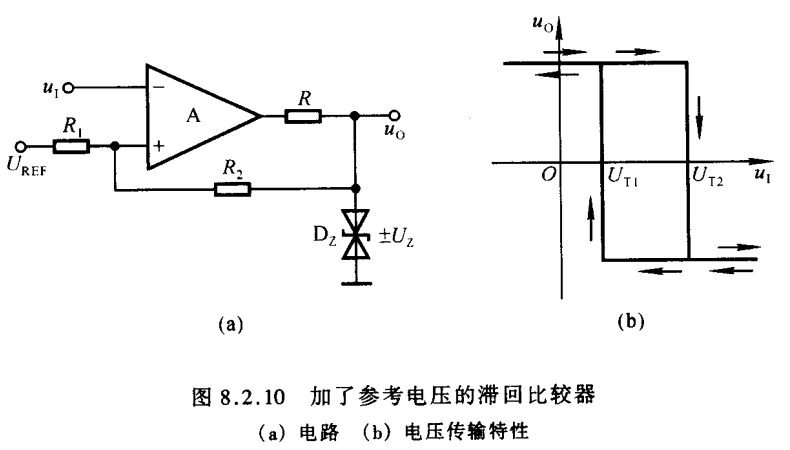
滞回的优点
- 可以提供一个噪声容限,在滞回范围内不会引起输出的改变,可以用于滤波
- 可以加快信号边沿
比较器应用-非正弦波发生电路
矩形波发生电路
如图,使用滞回电路组成了一个矩形波发生电路
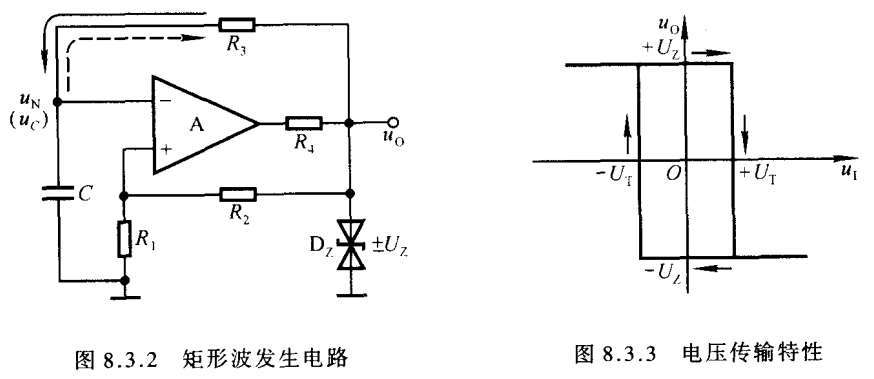
R3和C的引入给输入提供了一个RC充电回路,通过将输出uo反向引入到输入端,利用C电容的充放电以及滞回阈值电压UT改变的特性,该电路能自行产生方波
分析 :
若上电时,uo=+Uz,则阈值电压UT为正,uo通过R3给C充电,C的电压慢慢升高,当Uc>UT时,输出uo改变,uo=-Uz,阈值电压变为负,此时电容电压仍为正,所以对uo放电,Uc慢慢降低,当Uc<UT时,uo再次变为+Uz,如此循环就输出了矩形波(方波)。由于充放电回路一直,充放电时间也就一样。占空比是50%
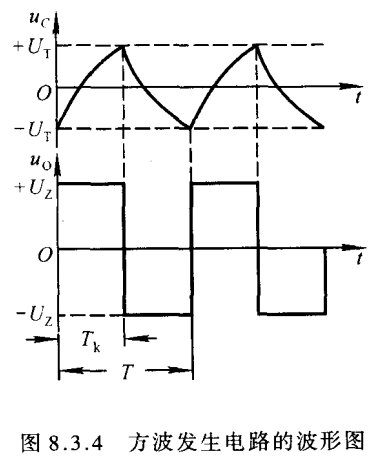
以上产生的是占空比不可调的方波,如想产生占空比可调的矩形波可以通过以下方式实现。既然矩形波的占空比是由电容的充放电时间决定的,那么给电容提供不同的充放电回路即可。而决定电流方向的器件当属二极管,如下图,通过调节电位计即可实现占空比调节。
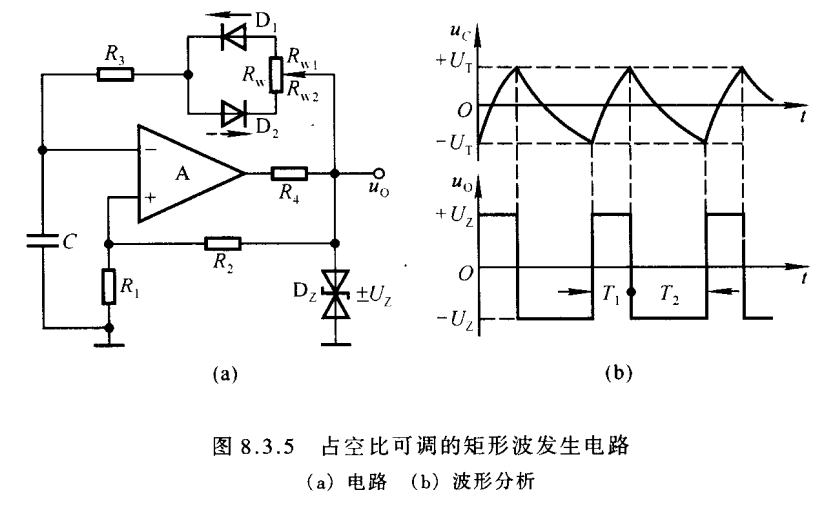
三角波发生电路
对矩形波进行积分就可以得到三角波,所以将上面的矩形波电路后级再接一个积分运算电路就能得到三角波了
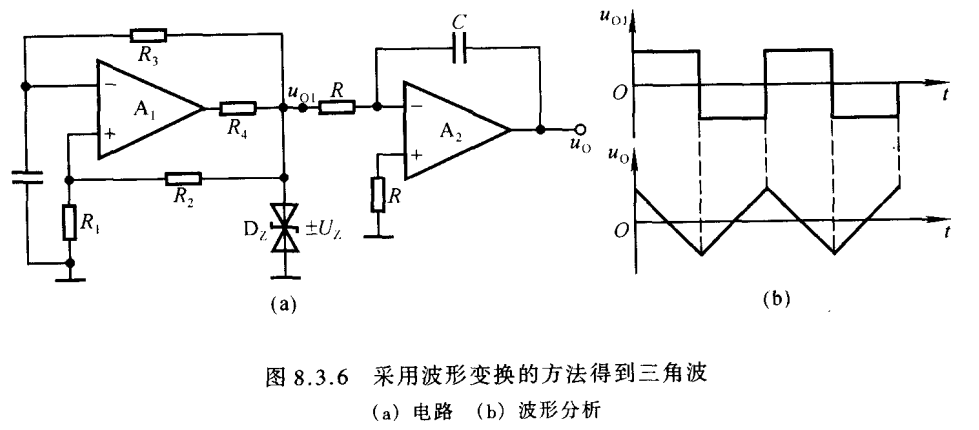
但是,考虑到电路简化,分析矩形波电路中的C的波形和三角波的功能一样,所以直接再将三角波输出接回到运放的输入端,就能替代之前的RC电路,但之前RC电路中电容电压上升时,uo=UT,这里由于积分电路的引入,方向反了,滞回将不会发挥作用。所以此时应该接到同向端P,电路最后如图
当然直接再积分电路后面再加一个反相器也行,但比较麻烦
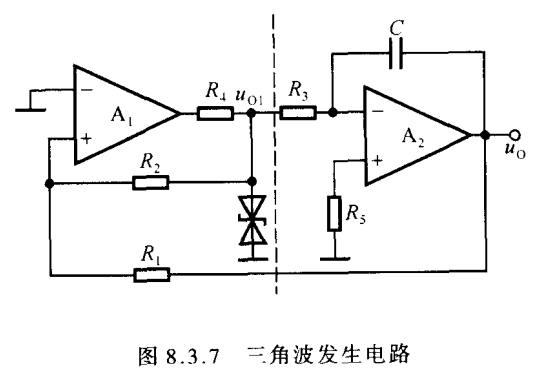
求UT
对于前面的滞回电路来说,uI就是现在的uo,输出就是uo1,所以它的UT就是uP=uN=0时的uo值
利用叠加定理
uP=R2R1+R2uO+R1R1+R2uO1 u_{P}=\frac{R_{2}}{R_{1}+R_{2}}u_{O}+\frac{R_{1}}{R_{1}+R_{2}}u_{O_{1}} uP=R1+R2R2uO+R1+R2R1uO1
令uP=0,得到UT
UT=−R1R2uO1,uO1=±UZ U_{T}=-\frac{R_{1}}{R_{2}}u_{O_{1}},u_{O_{1}}=\pm U_{Z} UT=−R2R1uO1,uO1=±UZ
所以,
uo1=+Uz时,UT−=−R1R2UZU_{T_{-}}=-\frac{R_{1}}{R_{2}}U_{Z}UT−=−R2R1UZ
uo1=-Uz时,UT+=R1R2UZU_{T_{+}}=\frac{R_{1}}{R_{2}}U_{Z}UT+=R2R1UZ
分析
电路刚上电,假设uo1正向饱和,则uO1=UZu_{O_{1}}=U_{Z}uO1=UZ,UTU_{T}UT为负,电容C开始充电,积分电路工作,uo负向增长,当uo负增长到等于UT−时,uP=0U_{T-}时,u_{P}=0UT−时,uP=0,继续负增长则滞回电路生效,uO1=−UZ,UT−变为UT+u_{O_{1}}=-U_{Z},U_{T-}变为U_{T+}uO1=−UZ,UT−变为UT+,电容C放电,uo开始正增长,当uo增长到等于uT+u_{T+}uT+时,uP再次等于0,继续增长则滞回电路生效,uo1再次反转,周而复始形成三角波输出
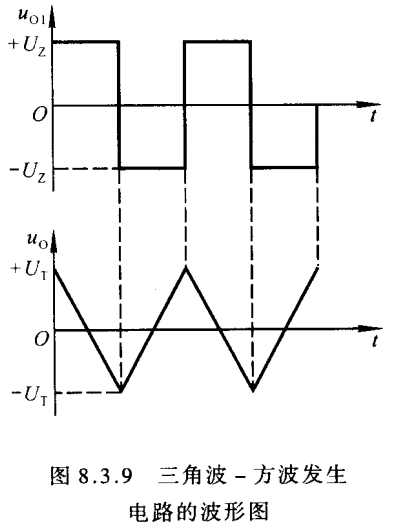
这里电容充放电的电流iC=iR=uO1R3i_{C}=i_{R}=\frac{u_{O_{1}}}{R_{3}}iC=iR=R3uO1,所以充放电的时间Tk=qi=CΔUi=C(UT+−UT)iC=CR3(UT+−UT)uO1T_{k}=\frac{q}{i}=\frac{C\Delta U}{i}=\frac{C(U_{T+}-U_{T})}{i_{C}}=\frac{CR_{3}(U_{T+}-U_{T})}{u_{O_{1}}}Tk=iq=iCΔU=iCC(UT+−UT)=uO1CR3(UT+−UT)
占空比是50%,所以整个周期T=2TkT=2T_{k}T=2Tk
如果想调节占空比就可加上二极管,如图a;
锯齿波发生器
如果将占空比做的很小,则输出的三角波下降沿很陡峭(操作就是将Rw的触头往上拨,减小上面充电时的电阻,提高充电电流,加大斜率),三角波就近似成了锯齿波,如图b
精密整流电路
提到整理,最先想到的一定是二极管,单个二极管可以实现半波整流,四个二极管形成的整流桥可以实现全波整流,但这些整流都是建立在输入信号幅值比较大,起码大于二极管导通压降的基础上来讨论的,当输入信号比较小时就需要专门的整流电路了。
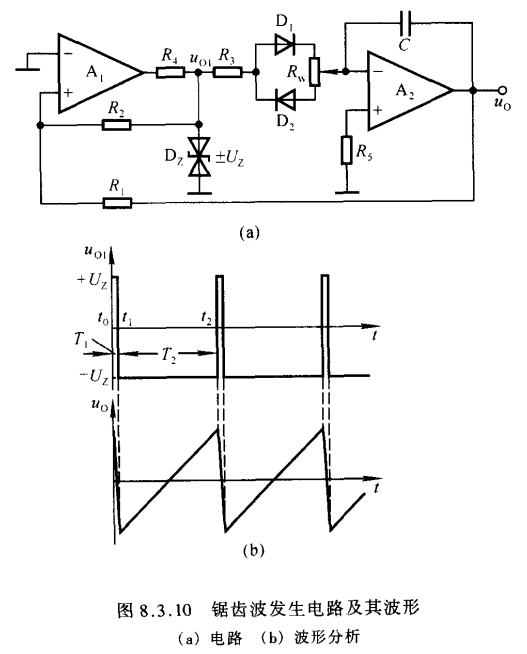
半波精密整流电路
如图实现了半波精密整流,它可以对输入信号进行半波整流,同时还能对输入信号进行一定的放大
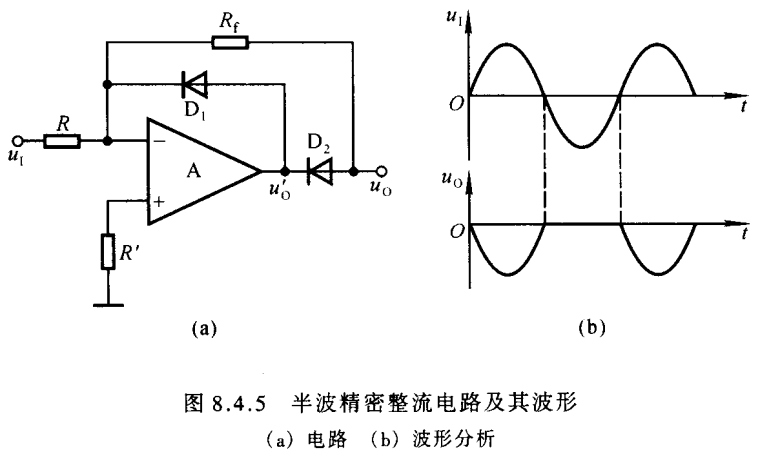
当uI>0时,uO′<0,D1截止,D2导通,形成反向比例运算电路;uO=−RfRuI当u_{I}>0时,u_{O}'<0,D_{1}截止,D_{2}导通,形成反向比例运算电路;u_{O}=-\frac{R_{f}}{R}u_{I}当uI>0时,uO′<0,D1截止,D2导通,形成反向比例运算电路;uO=−RRfuI
当uI<0时,uO′>0,D2截止,D1导通,uO=uN,A形成负反馈,uN=uP=0,所以此时uO=0当u_{I}<0时,u_{O}'>0,D_{2}截止,D_{1}导通,u_{O}=u_{N},A形成负反馈,u_{N}=u_{P}=0,所以此时u_{O}=0当uI<0时,uO′>0,D2截止,D1导通,uO=uN,A形成负反馈,uN=uP=0,所以此时uO=0
如何就形成了半波整流,如图b
由于使二极管导通的电压都是经过运放输出后的电压,所以对输入电压的要求就很低了,可以实现小信号的整流
全波精密整流电路
由上面电路很容易想到,若想获得全波整流,就把uI<0u_{I}<0uI<0时波形加上就行了,这种肯定可以实现,但还有一种更巧妙的方式,观察上面图b的波形可以发现,将半波整流的波形乘2倍再和原来的波形相叠加,再加负号反转就得到了全波整流。而反转相加的操作就是反向求和电路 ,所以Rf取2R后加上反向求和电路即实现全波整流,如下图
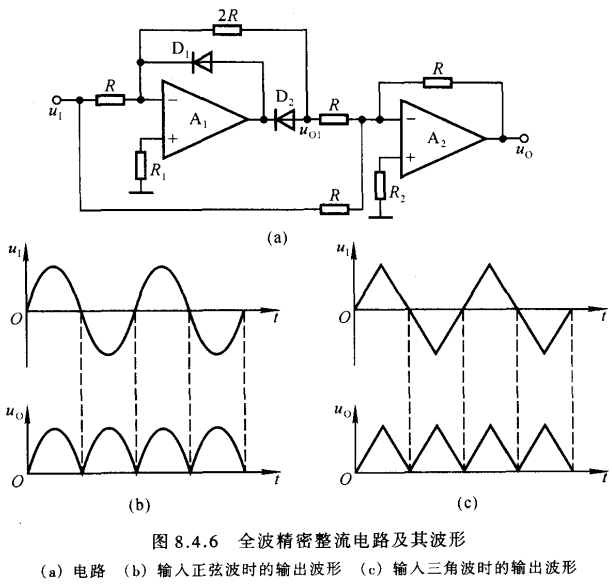
uI>0时,A1组成反向比例运算电路,u_{I}>0时,A_{1}组成反向比例运算电路,uI>0时,A1组成反向比例运算电路,uO1=−2uI;A2u_{O_{1}}=-2u_{I};A_{2}uO1=−2uI;A2组成反向求和电路,比例系数都是1,uO=−1∗(−2uI+uI)=uIu_{O}=-1*(-2u_{I}+u_{I})=u_{I}uO=−1∗(−2uI+uI)=uI
uI<0时,u_{I}<0时,uI<0时,uO1=0;A2u_{O_{1}}=0;A_{2}uO1=0;A2组成反向求和电路,一路是uIu_{I}uI,一路是uO1=0u_{O_{1}}=0uO1=0比例系数都是1,uO=−1∗(0+uI)=−uIu_{O}=-1*(0+u_{I})=-u_{I}uO=−1∗(0+uI)=−uI
所以将负半轴翻上去了,实现了全波整流