正弦波振荡电路
条件
- 要正反馈
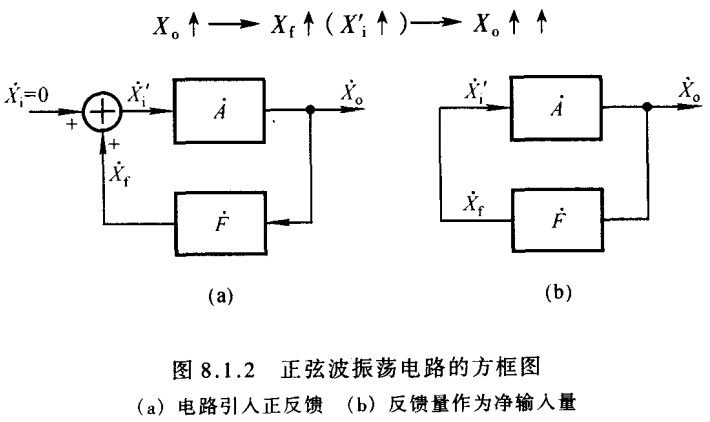
|图中的A并不是开环运放,而是一个完整的放大电路,如比例运算等 - 在某个频点∣A˙F˙∣>1|\dot{A}\dot{F}|>1∣A˙F˙∣>1
- 对于正反馈电路A和F引入的相位角之和要是2nΠ:φA+φF=2nπ\varphi_{A}+\varphi_{F}=2n\piφA+φF=2nπ,否则也可能负反馈,导致自激振荡停止
正弦波振荡电路组成
- 放大电路: 用于放大微弱信号
- 选频电路:选择特定频率进行放大输出
- 限幅电路:防止一直放大,从而导致饱和
- 正反馈
正弦振荡电路的判别
- 组成是否齐全
- 放大电路是否能正常工作
- 是否满足相位平衡条件:φA+φF=2nπ\varphi_{A}+\varphi_{F}=2n\piφA+φF=2nπ
- ∣A˙F˙∣>1|\dot{A}\dot{F}|>1∣A˙F˙∣>1
RC正弦波震荡电路
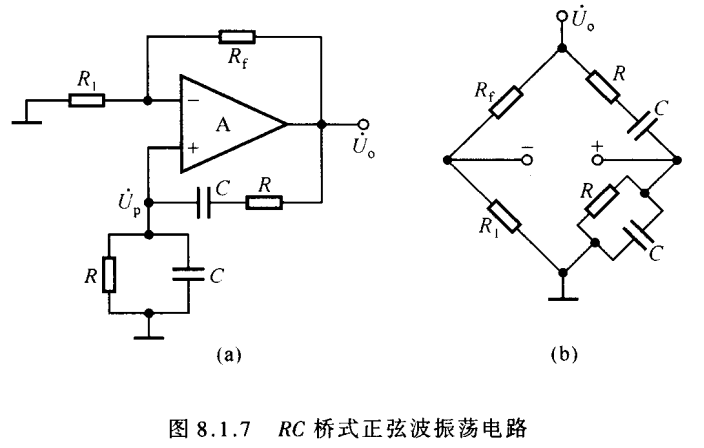
图a是由一个同向比例运算电路+一个RC选频电路组成
对于RC选频电路来说是个正反馈电路,电路启动瞬间会在Uo处产生一些噪声,这些噪声包含各个频率的分量,其中符合选频网络带通的频率会通过选频网络进入同向端,从而被放大,其它频率则被滤除,后面经过几个循环后选通的频率就能达到幅值的要求,这样就产生了特性频率的正弦波,完成了频率的发生
下图是选频网络部分
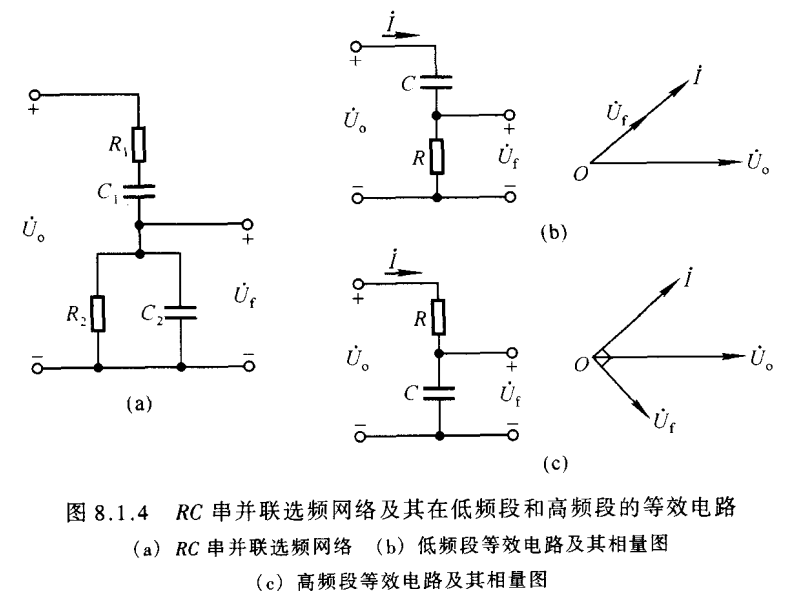
将电阻 R1R_1R1 与电容C1C_1C1串联、电阻R2R_2R2与电容 C2C_2C2并联所组成的网络称为 RC 串并联选频网络 .通常,选取 R1=R2=RR_1=R_2=RR1=R2=R,C1=C2=CC_1=C_2=CC1=C2=C
且该RC串并联网络同时起到了正反馈和选频电路的功能
分析
低频时:容抗较大,R1忽略,C2忽略,等效为图b高通电路;Uf相位超前Uo,当频率趋近0时,相位超前+90°,且Uf趋近于0
高频时:容抗较小,C1忽略,R2忽略,等效为图c低通电路;Uf相位落后Uo,当频率趋近∞时,相位落后-90°,且Uf趋近于0
所以当Uo的频率从0到∞时,必然有一个频率f0能使Uf和Uo相位同向,这个频率就是想要的选通频率
直接计算Uf对Uo的增益,有 F˙=U˙fU˙o=R//1jωCR+1jωC+R//1jωC\dot{F} = \frac{\dot{U}_f}{\dot{U}_o} = \frac{R//\frac{1}{j\omega C}}{R + \frac{1}{j\omega C} + R//\frac{1}{j\omega C}}F˙=U˙oU˙f=R+jωC1+R//jωC1R//jωC1
整理,可得 F˙=13+j(ωRC−1ωRC)\textcolor{red}{\dot{F} = \frac{1}{3 + j\left(\omega RC - \frac{1}{\omega RC}\right)}} F˙=3+j(ωRC−ωRC1)1
想要Uf和Uo相位同向,所得式子中就不能有虚数部分,所以
令ω0=1RC\omega_0 = \frac{1}{RC}ω0=RC1,则 f0=12πRC\textcolor{red}{f_0 = \frac{1}{2\pi RC} \quad} f0=2πRC1
也就是说,该RC串并联电路只会允许频率为f0的频率通过,其它的频率不满足正反馈原理,都会逐渐消失。
此时F˙=13\dot{F}=\frac{1}{3}F˙=31
代入上式,得出 F˙=13+j(ff0−f0f)\dot{F} = \frac{1}{3 + j\left(\frac{f}{f_0} - \frac{f_0}{f}\right)} \quadF˙=3+j(f0f−ff0)1
幅频特性为 ∣F˙∣=132+(ff0−f0f)2|\dot{F}| = \frac{1}{\sqrt{3^2 + \left(\frac{f}{f_0} - \frac{f_0}{f}\right)^2}} \quad∣F˙∣=32+(f0f−ff0)2 1
相频特性为 φF=−arctan13(ff0−f0f)\varphi_F = -\arctan \frac{1}{3}\left(\frac{f}{f_0} - \frac{f_0}{f}\right) \quad φF=−arctan31(f0f−ff0)
其幅频和相频曲线如下图,不仅在f0处选频,而且此时输出增益最大
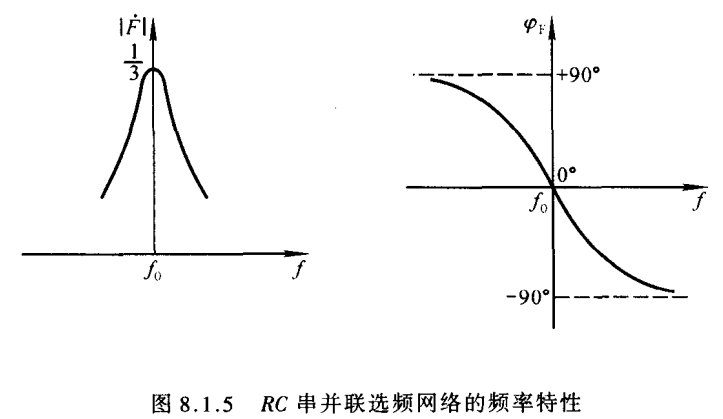
当然,因为选频网络在f0处的增益是13\frac{1}{3}31,所以要使∣A˙F˙∣>1|\dot{A}\dot{F}|>1∣A˙F˙∣>1,需要满足∣A˙∣>3|\dot{A}|>3∣A˙∣>3
这里的分析思路和晶振的皮尔斯震荡电路原理很像,晶振能输出特定频率也是加强了相位为2nπ2n\pi2nπ的频率,然后逐渐放大输出
解决了选频和正反馈,以及∣A˙F˙∣>1|\dot{A}\dot{F}|>1∣A˙F˙∣>1,为了稳定还需要限幅电路,使得在达到想要是输出幅值时,不再继续放大,也就是A增益要减小,当A=3时电路就能稳定输出特定幅值特定频率的正弦波了。
对于上面RC桥式正弦波震荡电路来说,它的A就是同相比例运算的增益A=1+RfR1A=1+\frac{R_{f}}{R_{1}}A=1+R1Rf,既然想让A慢慢变低,就只需要让Rf随电流或者温度的升高而降低就行了。而二极管就具备这种特性,二极管的动态电阻rdr_{d}rd会电流的升高而降低,所以将Rf反馈部分电路改成如下图即可达到目的
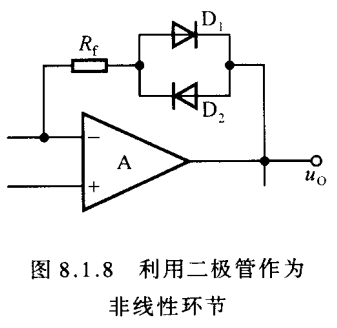
这里加俩二极管是因为输出信号是交流信号,要双向导通
缺点
- 频率不能很高 :频率高的话R和C就会很小,当小到一定程度时运放输出电阻Ro和运放中晶体管的极间电容C都不可忽略了,此时选频频率就会受影响。它的选频频率通常在1MHz以内
LC正弦波振荡电路
一样的,注重思路
首先,LC并联电路有个特点,它在谐振时阻抗很大,低频和高频时阻抗又很小。它本身就具有选频的功能。
另外,又知在三极管放大电路中,Rc越大,放大倍数就越大,那这个LC并联电路就很适合作为Rc电阻。现在把LC并联电路替换掉Rc电阻则有
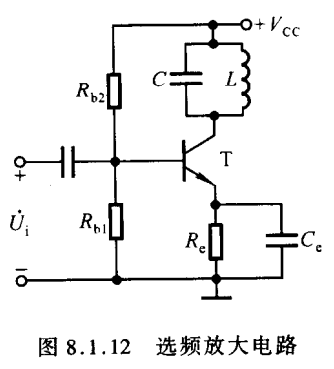
它只在LC谐振频率处放大倍数很大,高低频放大倍数很小,也就是说一堆各种频率的信号进入到Ui时,只有LC谐振频率的信号被大幅放大,相当于这个频率被筛选出来了(这个LC替换Rc电阻的思路非常棒!)
虽然这个频率被选出来了,当只经过一轮放大远远不够,因为输入信号一般都比较微弱,还需要想办法把这个信号重新引回到输入端进行循环。而变压器就能很好地实现这个目的,如图所示,使用变压器不仅能将输入信号重新引回到输入端,同时还有隔离的作用,这就是变压器反馈式振荡电路
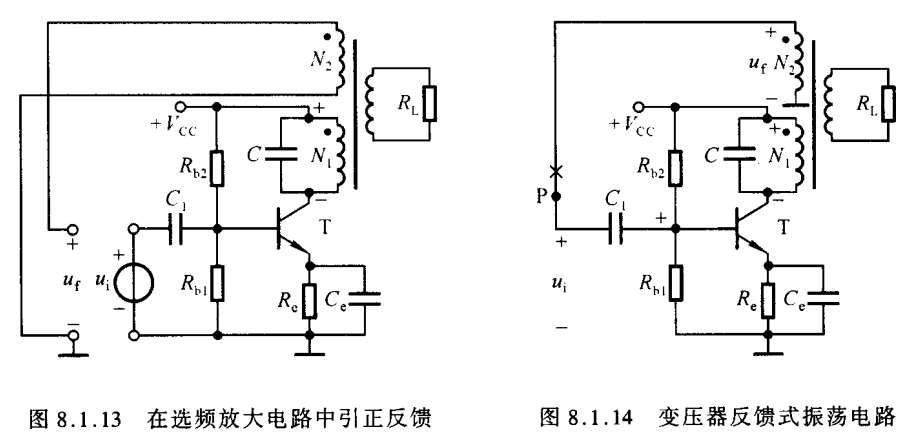
但要注意,引回来的次级绕组要从同名端出来,从而构成正反馈
考虑到原副边的绕法需要磁隙,从而会有漏磁,所以使用电感抽头的方式改成以下电路
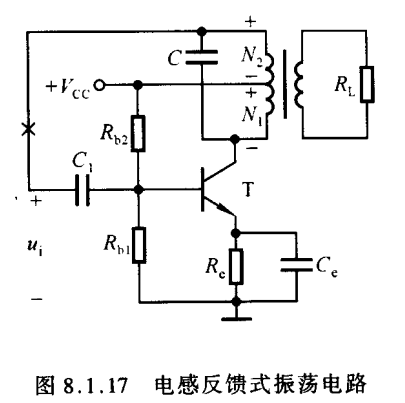
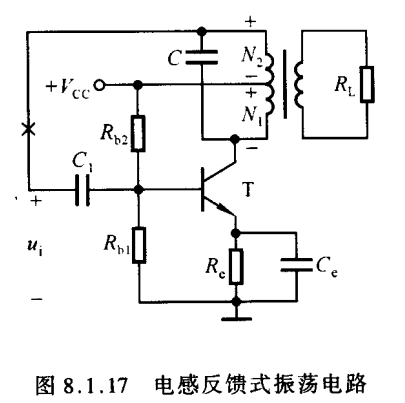
这就构成了电感反馈式振荡电路
但电感天然对高次谐波比较敏感,高次谐波也会引入到输入端,造成波形失真,所以改进的方式就是使用电容,从电容中间抽的话可以使用两个电容串联然后从中间取,如下图
构成电容反馈式振荡电路,这样接的目的是要形成正反馈