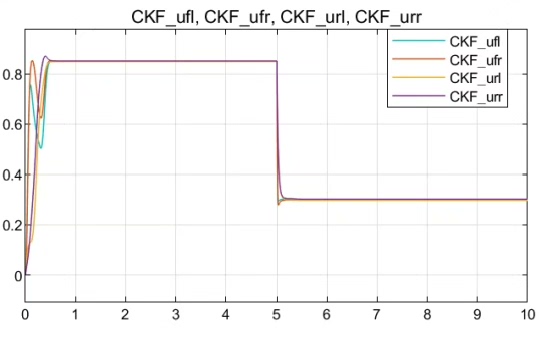
分布式驱动电动汽车路面附着系数估计：无迹卡尔曼与容积卡尔曼滤波大比拼

②基于分布式驱动电动汽车的路面附着系数估计，分别采用无迹卡尔曼滤波和容积卡尔曼滤波对电动汽车四个车轮的路面附着系数进行估计。本模型参考sci二区顶刊，开发了分布式驱动电动汽车路面附着系数估计的进阶版本，可在高速，低速下，对开路面，对接路面四种组合工况下对路面附着系数进行准确估计估计。该模型利用无迹卡尔曼滤波，容积卡尔曼滤波对路面附着系数分别进行估计，容积卡尔曼和无迹卡尔曼均由S- function编写，可比较二种滤波的估计效果。 Carsim和simulink联合仿真，高附着路面0.85，低附着路面0.3，对接路面

在电动汽车的世界里，路面附着系数估计可是个关键技术，就好比我们开车要清楚路面是干是湿，能不能稳稳地加速、刹车和转弯。今天就来聊聊基于分布式驱动电动汽车的路面附着系数估计，这里用到了无迹卡尔曼滤波（UKF）和容积卡尔曼滤波（CKF）两种方法。

模型背景

这次开发的模型可是参考了sci二区顶刊，是分布式驱动电动汽车路面附着系数估计的进阶版本。它厉害的地方在于，不管是高速还是低速行驶，也不管是在对开路面（左右两侧路面附着系数不同）还是对接路面（前后路面附着系数不同），这四种组合工况下都能准确地估计路面附着系数。这就好比一个超级导航，能在各种复杂路况下为电动汽车提供精准的路面信息。

滤波方法实现

无迹卡尔曼滤波（UKF）与容积卡尔曼滤波（CKF）

我们利用无迹卡尔曼滤波和容积卡尔曼滤波分别对路面附着系数进行估计。而且这两种滤波都是由S - function编写的，这样方便我们比较它们的估计效果。下面简单介绍一下这两种滤波。

无迹卡尔曼滤波（UKF）是一种非线性滤波方法，它通过一组确定性采样点（Sigma点）来近似系统的概率分布，避免了传统卡尔曼滤波中线性化带来的误差。容积卡尔曼滤波（CKF）也是一种非线性滤波，它基于容积准则来选择采样点，能更有效地处理非线性系统。

代码示例与分析

这里给出一个简单的S - function编写的容积卡尔曼滤波的伪代码示例：

matlab 复制代码

function [sys,x0,str,ts] = CKF_Sfunction(t,x,u,flag)
    switch flag
        case 0 % 初始化
            sizes = simsizes;
            sizes.NumContStates  = 0;
            sizes.NumDiscStates  = 1; % 假设状态变量只有一个
            sizes.NumOutputs     = 1;
            sizes.NumInputs      = 1;
            sizes.DirFeedthrough = 0;
            sizes.NumSampleTimes = 1;
            sys = simsizes(sizes);
            x0  = [0]; % 初始状态
            str = [];
            ts  = [0.01 0]; % 采样时间
        case 1 % 连续状态更新，这里没有连续状态，所以不做处理
            sys = [];
        case 2 % 离散状态更新
            % 容积卡尔曼滤波核心步骤
            % 预测步骤
            x_pred = f(x,u); % 状态预测方程
            P_pred = F*P*F' + Q; % 协方差预测方程
            % 更新步骤
            y_pred = h(x_pred); % 观测预测方程
            S = H*P_pred*H' + R; % 观测协方差
            K = P_pred*H'*inv(S); % 卡尔曼增益
            x = x_pred + K*(u - y_pred); % 状态更新
            P = (eye(size(P)) - K*H)*P_pred; % 协方差更新
            sys = [x];
        case 3 % 输出计算
            sys = x;
        case 4 % 采样时间
            sys = [];
        case 9 % 终止
            sys = [];
        otherwise
            error(['Unhandled flag = ',num2str(flag)]);
    end
end

这段代码是一个简单的容积卡尔曼滤波的S - function实现。在初始化部分（case 0），我们设置了状态变量、输入输出的数量以及采样时间等信息。在离散状态更新部分（case 2），实现了容积卡尔曼滤波的核心步骤，包括预测和更新。预测步骤通过状态预测方程和协方差预测方程得到预测状态和预测协方差，更新步骤则根据观测值对状态和协方差进行更新。最后在输出计算部分（case 3），将更新后的状态作为输出。

联合仿真

我们采用Carsim和Simulink联合仿真，设置了高附着路面（附着系数为0.85）和低附着路面（附着系数为0.3）以及对接路面的工况。通过仿真，我们可以直观地看到无迹卡尔曼滤波和容积卡尔曼滤波在不同工况下对路面附着系数的估计效果。

通过对比两种滤波的估计结果，我们可以分析出它们在不同工况下的优缺点。比如，在高速行驶且路面情况复杂时，哪种滤波方法能更快更准确地估计出路面附着系数；在低速行驶时，它们的估计精度又如何。

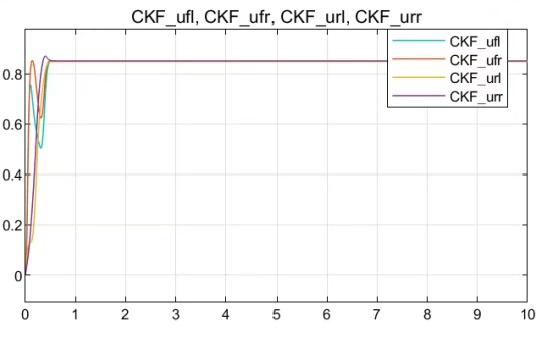
总之，这次基于分布式驱动电动汽车的路面附着系数估计的研究，通过无迹卡尔曼滤波和容积卡尔曼滤波的对比，为电动汽车在不同路况下的安全行驶提供了更可靠的路面信息。未来，我们还可以进一步优化这两种滤波方法，让电动汽车的行驶更加智能和安全。