目录
动量法:优化梯度下降的"惯性"策略
梯度下降是优化模型参数的核心方法,但其基础版本在训练中常面临收敛慢、震荡大的问题。
动量法通过引入物理中的"惯性"概念,有效提升了优化效率与稳定性。
核心原理
动量法在更新参数时,不仅考虑当前梯度,还累积历史梯度的指数加权平均作为"动量",使更新方向更平滑、更一致。
更新公式:
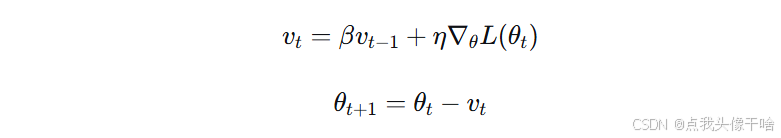
-
vt:当前时刻的动量(速度)
-
β:动量系数(通常0.9),控制历史信息的保留程度
-
η:学习率
-
∇θL(θt):当前梯度
与SGD的直观对比
普通SGD :每次更新只依赖当前梯度,路径曲折,易震荡。
动量法:更新受历史动量引导,在稳定方向加速,在震荡方向减速,路径更平滑直接。
关键推导
动量更新可视为历史梯度的指数加权和:
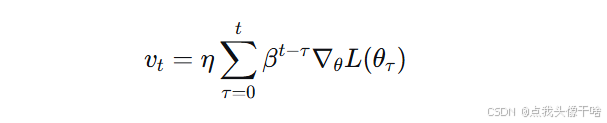
当损失函数在某方向持续下降时,同向梯度不断累积,实现加速;当梯度方向频繁变化时,正负梯度相互抵消,抑制震荡。
简洁案例
优化目标:最小化 L(w)=(w−4)2,最优值 w∗=4。
SGD更新(η=0.1):
wt+1=wt−0.1×2(wt−4)
动量法更新(η=0.1,β=0.9):
vt=0.9vt−1+0.1×2(wt−4)
wt+1=wt−vt
初始化 w0=0,v0=0:
-
第一步:梯度=-8,SGD更新至0.8;动量法 v1=−0.8,更新至0.8
-
第二步:梯度=-6.4,SGD更新至1.44;动量法 v2=0.9×(−0.8)+0.1×(−6.4)=−1.36,更新至2.16
可见,动量法因累积了之前的梯度,第二步更新幅度更大,加速接近最优值。
Python实现对比
python
import numpy as np
import matplotlib.pyplot as plt
# 定义目标函数及其梯度
def loss(w):
return (w - 4)**2
def grad(w):
return 2 * (w - 4)
# 优化器
def sgd_update(w, lr):
return w - lr * grad(w)
def momentum_update(w, v, lr, beta):
v = beta * v + lr * grad(w)
return w - v, v
# 参数设置
lr = 0.1
beta = 0.9
iterations = 20
# 初始化
w_sgd = 0
w_mom = 0
v = 0
# 记录路径
path_sgd = [w_sgd]
path_mom = [w_mom]
# 迭代优化
for i in range(iterations):
w_sgd = sgd_update(w_sgd, lr)
w_mom, v = momentum_update(w_mom, v, lr, beta)
path_sgd.append(w_sgd)
path_mom.append(w_mom)
# 可视化
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
w_range = np.linspace(-1, 5, 100)
plt.plot(w_range, loss(w_range), 'k-', alpha=0.3, label='Loss')
plt.plot(path_sgd, loss(np.array(path_sgd)), 'o-', label='SGD', markersize=4)
plt.plot(path_mom, loss(np.array(path_mom)), 's-', label='Momentum', markersize=4)
plt.xlabel('Parameter w')
plt.ylabel('Loss')
plt.title('Optimization Trajectory')
plt.legend()
plt.grid(True, alpha=0.3)
plt.subplot(1, 2, 2)
plt.plot(range(len(path_sgd)), loss(np.array(path_sgd)), label='SGD')
plt.plot(range(len(path_mom)), loss(np.array(path_mom)), label='Momentum')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss Convergence')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()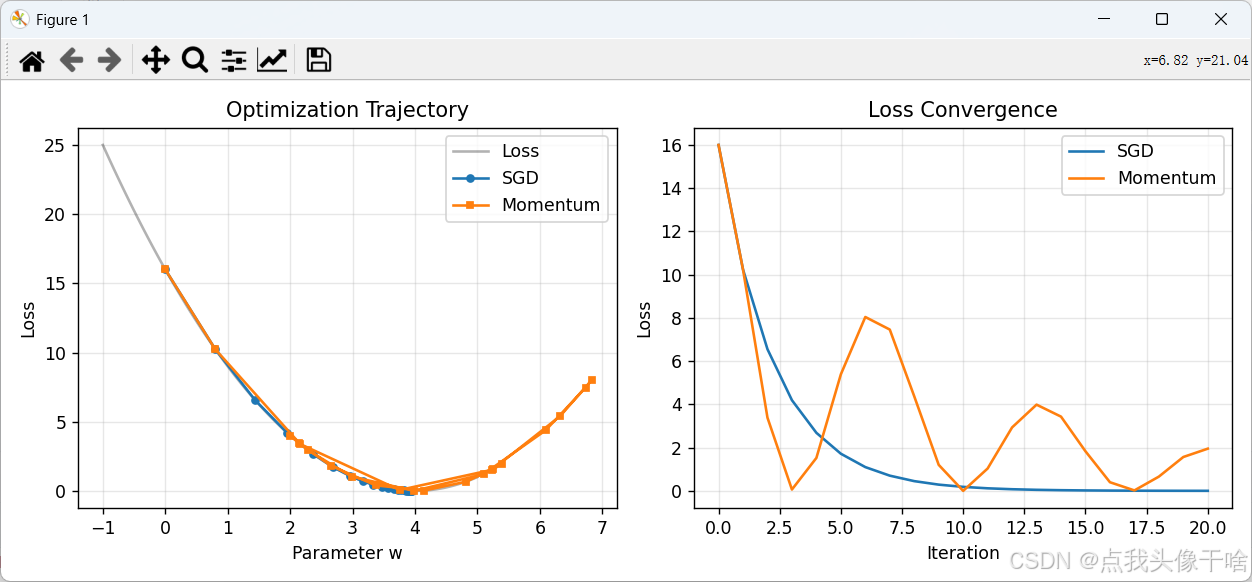
算法优劣
优点:
-
加速收敛:在平缓或方向一致的区域快速前进
-
抑制震荡:平滑优化路径,提升训练稳定性
-
帮助逃离局部极小:惯性可能冲过窄小局部最优点
缺点:
-
增加超参数:需调整动量系数β
-
可能超调:动量过大时在最优值附近震荡
适用场景:
-
高维非凸优化(如深度学习)
-
梯度存在噪声或方向不一致时
-
需要更快收敛速度的场景
核心总结
动量法通过累积历史梯度信息,为参数更新增加"惯性",在保持随机梯度下降计算效率的同时,显著改善了优化过程的收敛速度与稳定性。其核心思想简单而有效,已成为现代深度学习优化器的基础组件之一。