算法设计与分析
题源1 斐波那契数列应用
重点考察：递归方法实现时的递归方程的书写！
如果只有一级台阶，则 f(1)= ++1++
如果有两级台阶，则 f(2)= ++2++
给出其递归表达式，f(n)=f(n−1)+f(n−2)f(n) = f(n-1)+f(n-2)f(n)=f(n−1)+f(n−2)
题源2 背包问题
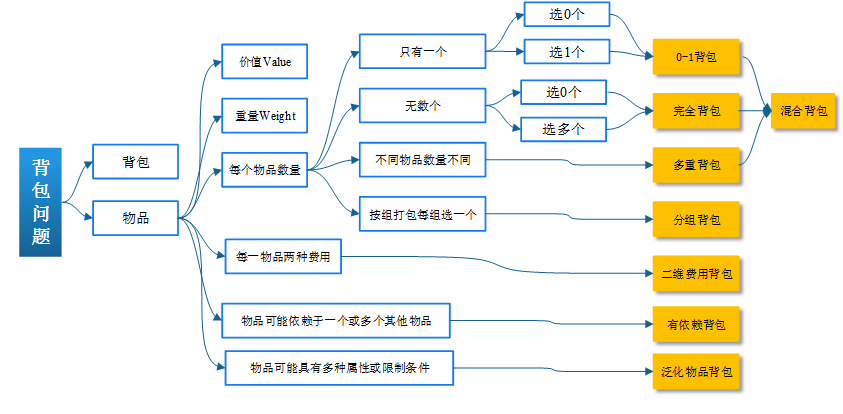
聚焦0-1背包问题，关注填表法！
动态规划过程：
（1)定义状态
设DP[i][j]DP[i][j]DP[i][j]表示在前iii个物品中，当前背包容量为jjj时，能够装入背包的物品的最大价值。
（2）状态转移方程
对于每个物品，有两种选择：放入背包或不放入背包。因此DP[i][j]DP[i][j]DP[i][j]的值取决于两种情况的最大值：
●不放入第iii个物品，则DP[i][j]=DP[i−1][j]DP[i][j]=DP[i-1][j]DP[i][j]=DP[i−1][j]（即前i−1i-1i−1个物品在容量为j的背包中的最大价值）。
●放入第iii个物品，但前提是背包的剩余容量要大于等于该物品的重量，即j>=wt[i]j>=wt[i]j>=wt[i]，此时DP[i][j]=DP[i−1][j−wt[i]+val[i]DP[i][j]=DP[i-1][j-wt[i]+val[i]DP[i][j]=DP[i−1][j−wt[i]+val[i]（即前i−1i-1i−1个物品在容量为j−wt[i]j-wt[i]j−wt[i]的背包中的最大价值加上第iii个物品的价值）。
综合两种情况，得到状态转移方程：
{DP[i][j]=max(DP[i−1][j−wt[i]]+val[i],DP[i−1][j]);(j≥wt[i])DP[i][j]=DP[i−1][j](j<wt[i]) \begin{cases}\mathrm{DP[i][j]=max(DP[i-1][j-wt[i]]+val[i],DP[i-1][j]);}&\mathrm{(j\geq wt[i])}\\\mathrm{DP[i][j]=DP[i-1][j]}&\mathrm{(j<wt[i])}&\end{cases} {DP[i][j]=max(DP[i−1][j−wt[i]]+val[i],DP[i−1][j]);DP[i][j]=DP[i−1][j](j≥wt[i])(j<wt[i])
（3）边界条件
①DP[0][j]=0DP[0][j]=0DP[0][j]=0对于所有jjj，因为没有物品可选时，无论背包容量多大，总价值都是0。
②DP[i][0]=0DP[i][0]=0DP[i][0]=0对于所有i，因为背包容量为0时，无法装入任何物品，总价值为0。
(4)） 目标
最终目标是找到DP[n][w]DP[n][w]DP[n][w]，其中nnn是物品的总数，www是背包的最大承重，这表示在所有物品和背包容量限制下，能够装入背包的物品的最大价值。
例题：
当解决0-1背包问题时，动态规划常用的方法是通过填表的方式来求解。下面将通过示例详细展示填表的过程，并解释每一步的计算过程。 假设有如下物品重量、物品价值和背包所能承受的参数，
- 物品重量：[2, 3, 6, 5]
- 物品价值：[6, 3, 5, 4]
- 背包所能承受的质量（容量）：9
填表过程：
（1）创建二维表格DP，并进行表格初始化：行数据表示物品的选择，列数据表示背包的容量j容量j容量j。
| j | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 物品i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| i=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| i=1 | w=2, v=6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i=2 | w=3, v=3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i=3 | w=6, v=5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i=4 | w=5, v=4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
（2）填表
依据状态转移方程，逐行更新表格数据。
{DP[i][j]=max(DP[i−1][j−wt[i]]+val[i],DP[i−1][j]);(j≥wt[i])DP[i][j]=DP[i−1][j](j<wt[i]) \begin{cases}\mathrm{DP[i][j]=max(DP[i-1][j-wt[i]]+val[i],DP[i-1][j]);}&\mathrm{(j\geq wt[i])}\\\mathrm{DP[i][j]=DP[i-1][j]}&\mathrm{(j<wt[i])}&\end{cases} {DP[i][j]=max(DP[i−1][j−wt[i]]+val[i],DP[i−1][j]);DP[i][j]=DP[i−1][j](j≥wt[i])(j<wt[i])
| j | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 物品i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| i=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| i=1 | w=2, v=6 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| i=2 | w=3, v=3 | 0 | 0 | 6 | 6 | 6 | 9 | 9 | 9 | 9 | 9 |
| i=3 | w=6, v=5 | 0 | 0 | 6 | 6 | 6 | 9 | 9 | 9 | 11 | 11 |
| i=4 | w=5, v=4 | 0 | 0 | 6 | 6 | 6 | 9 | 9 | 10 | 11 | 11 |
更新DP[1][2]DP[1][2]DP[1][2]：因为(j≥wt[i])即(2≥wt[1])\mathrm{(j\geq wt[i])} 即 \mathrm{(2\geq wt[1])}(j≥wt[i])即(2≥wt[1]) 满足状态转移的第一种情况，所以 DP[i][j]=max(DP[i-1][j-wt[i]]+val[i],DP[i-1][j])
即DP[1][2]=max(DP[1−1][2−wt[1]]+val[1],DP[1−1][2])即 DP[1][2]=max(DP[1-1][2-wt[1]]+val[1],DP[1-1][2])即DP[1][2]=max(DP[1−1][2−wt[1]]+val[1],DP[1−1][2])
=max(DP[0][2−2]+val[1],DP[1−1][2])=max(DP[0][2-2]+val[1],DP[1-1][2])=max(DP[0][2−2]+val[1],DP[1−1][2])
=max(0+6],0)=6=max(0+6],0) = 6=max(0+6],0)=6
同理更新DP[2][3]DP[2][3]DP[2][3]：因为(j≥wt[i])即(3≥wt[2])\mathrm{(j\geq wt[i])} 即 \mathrm{(3\geq wt[2])}(j≥wt[i])即(3≥wt[2]) 满足状态转移的第一种情况
DP[2][3]=max(DP[2−1][3−wt[2]]+val[2],DP[2−1][3])DP[2][3]=max(DP[2-1][3-wt[2]]+val[2],DP[2-1][3])DP[2][3]=max(DP[2−1][3−wt[2]]+val[2],DP[2−1][3])
=max(DP[1][3−3]+val[2],DP[2−1][3])=max(DP[1][3-3]+val[2],DP[2-1][3])=max(DP[1][3−3]+val[2],DP[2−1][3])
=max(0+3],6)=6=max(0+3],6) = 6=max(0+3],6)=6
DP[2][5]=max(DP[2−1][5−wt[2]]+val[2],DP[2−1][5])DP[2][5]=max(DP[2-1][5-wt[2]]+val[2],DP[2-1][5])DP[2][5]=max(DP[2−1][5−wt[2]]+val[2],DP[2−1][5])
=max(DP[1][5−3]+val[2],DP[2−1][5])=max(DP[1][5-3]+val[2],DP[2-1][5])=max(DP[1][5−3]+val[2],DP[2−1][5])
=max(6+3],6)=9=max(6+3],6) = 9=max(6+3],6)=9
通过不断填表更新，最终得到的右下角的值即为问题的最优解，即DP[4][9]DP[4][9]DP[4][9]。若想知道具体的物品选择方案，需要进行倒退：
需要倒过来观察：
DP[4][9]=max(DP[3][4]+4,DP[3][9])=DP[3][9]DP[4][9]=max(DP[3][4]+4,DP[3][9])=DP[3][9]DP[4][9]=max(DP[3][4]+4,DP[3][9])=DP[3][9]，说明没有装物品4，i4=0i_4 =0i4=0；
DP[3][9]=max(DP[2][3]+5,DP[2][9])=DP[2][3]+5=11DP[3][9]=max(DP[2][3]+5,DP[2][9])=DP[2][3]+5=11DP[3][9]=max(DP[2][3]+5,DP[2][9])=DP[2][3]+5=11，说明装了物品3，i3=1i_3 =1i3=1；
DP[2][3]=max(DP[1][0]+3,DP[1][3])=DP[1][3]DP[2][3]=max(DP[1][0]+3,DP[1][3])=DP[1][3]DP[2][3]=max(DP[1][0]+3,DP[1][3])=DP[1][3]，说明没有装物品2，i2=0i_2 =0i2=0；
DP[1][3]=max(DP[0][1]+6,DP[0][3])=DP[0][1]+6=6DP[1][3]=max(DP[0][1]+6,DP[0][3])=DP[0][1]+6=6DP[1][3]=max(DP[0][1]+6,DP[0][3])=DP[0][1]+6=6，说明装了物品1，i1=1i_1 =1i1=1。
题源3 最短路径之Dijkstra算法求解
要求：能够写出最终输出的结果
DijkstraDijkstraDijkstra 算法也称为最短路径算法，是一种寻找图中单源最短路径 的算法，适用于非负权重的所有情况。
是贪心策略的经典例子，从一个起始点开始，逐步扩展到图中的所有其他节点，每次选择未访问的最近节点，并更新其临近节点的距离。用来解决单源点到其余顶点的最短路径问题。
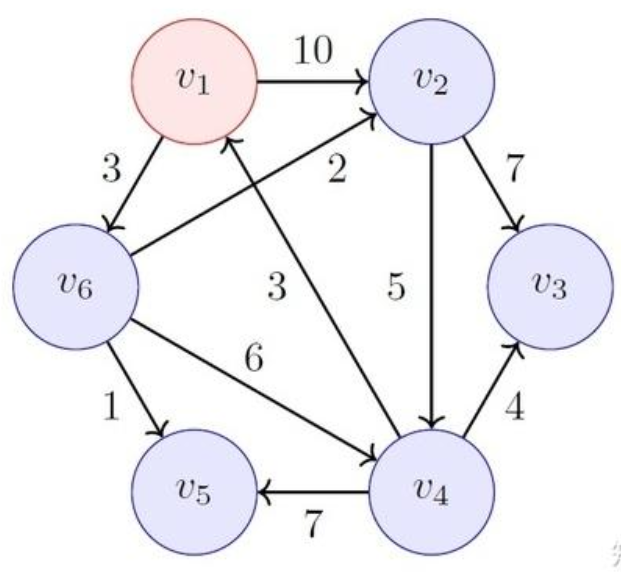
v1到其他顶点的距离如下：
| v2 | v3 | v4 | v5 | v6 | |
|---|---|---|---|---|---|
| 最短距离 | 5 | 12 | 9 | 4 | 3 |
| 具体路径 | v1-v6-v2 | v1-v6-v2-v3 | v1-v6-v4 | v1-v6-v5 | v1-v6 |
| B | C | D | E | F | |
|---|---|---|---|---|---|
| 最短距离 | 1 | 3 | 4 | 4 | 7 |
| 具体路径 | A-B | A-B-C | A-B-D | A-B-D-E | A-B-D-F |
题源4 高精度加法
简答题考察点 ①字符串的模拟 ②如何处理进位
用字符串和数组来表示高精度数值，每个字符或数组元素代表数值的一个数字或一组数字；采用分治策略解决高精度相加问题，其基本思想是将高精度的加法分解为更小的加法操作，然后将这些结果合并起来得到最终结果。
具体实现：
（1）分解：将高精度分解为更小的数位。
（2）递归计算：对分解后的每个数位进行递归的加法计算。如果数位相加的结果超过了数据类型所能表示的范围，需要进行进位处理。
（3）合并：将递归计算得到的结果按顺序合并起来，形成最终的高精度加法结果。
（4）处理进位：在合并过程中，如果高位相加结果超过数据类型所能表示的范围，需要特别处理进位。
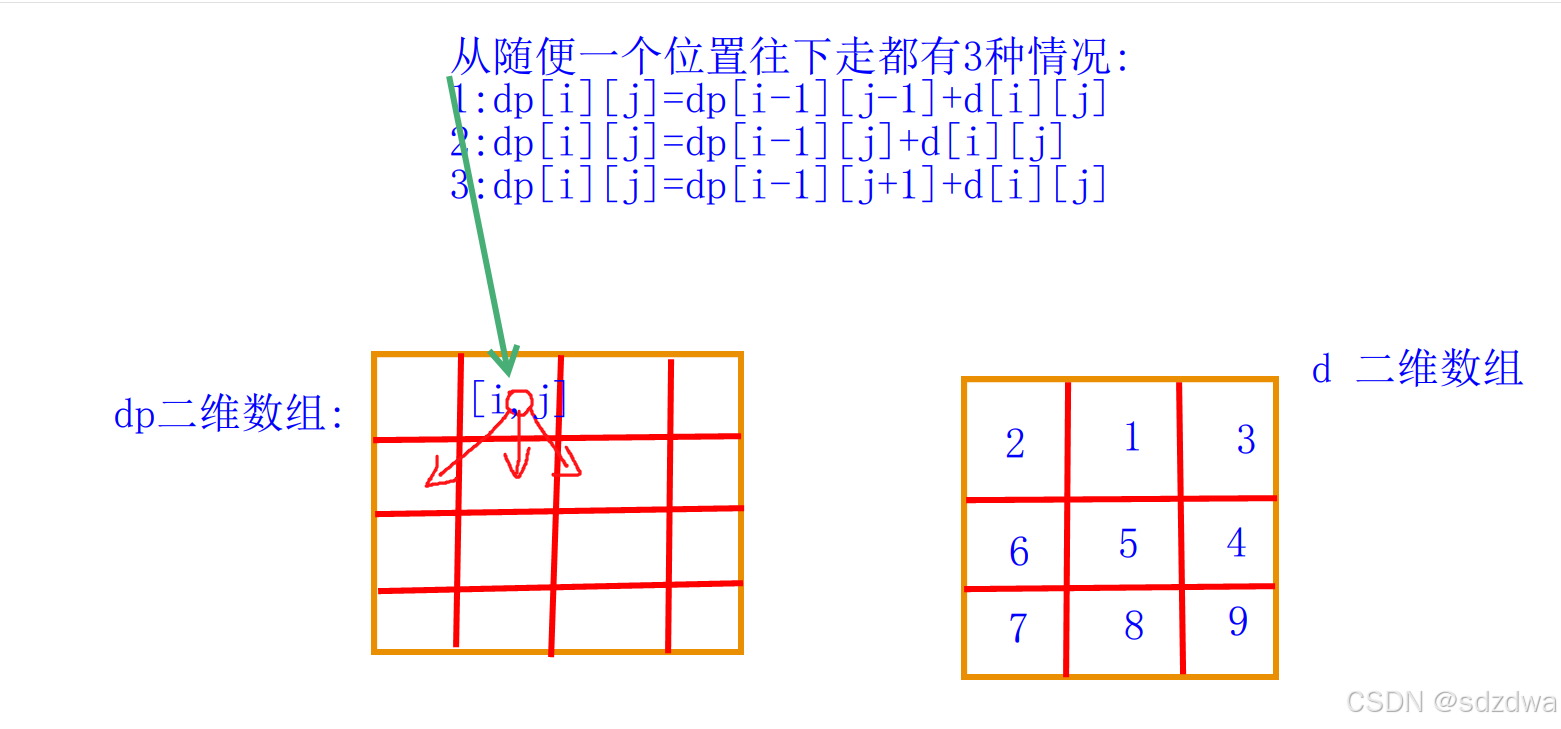
题源6 最小路径和
考察形式：填表
题源7 删数问题
考察删数的规则，能够写出每一步应该删除的数字！
贪心策略 ：每次删除一个数字时，优先删除对当前序列字典序列影响最大的数字。找到系列中第一个满足D[j]>D[j+1]D[j]>D[j+1]D[j]>D[j+1]的数字D[j]D[j]D[j]，并将其删除。如果整个序列是非递减的，则删除最后一个数字。
题源8 n皇后问题
共有几种解法，能够手工画出来所有的方案----> 原理思想
回溯算法的试错思维：
采用深度优先搜索策略遍历问题的解空间，在探索过程中逐步构建候选解，并在发现当前路径无法构成有效解时立即回退到上一步状态。
适合解决需要枚举所有可能组合或排列的决策类问题，通过维护动态的"当前解"状态，在满足特定条件时记录有效解，不满足时则撤销最近的选择并尝试其他可能性。
解决N皇后问题的核心思路是通过回溯法来逐行地尝试放置皇后，并在每一步检查是否合法。合法的放置方式会继续递归到下一行，不合法的放置方式会回溯到上一步进行调整。回溯法的基本思想是递归地尝试每一种可能的放置，并在发现冲突时回溯，换一个位置继续尝试。
当n=1时，只有一种解决方案。
当n=2时，无解。
当n=3时，无解。
当n=4时，有2种解决方案。
当n=5时，有10种解决方案。
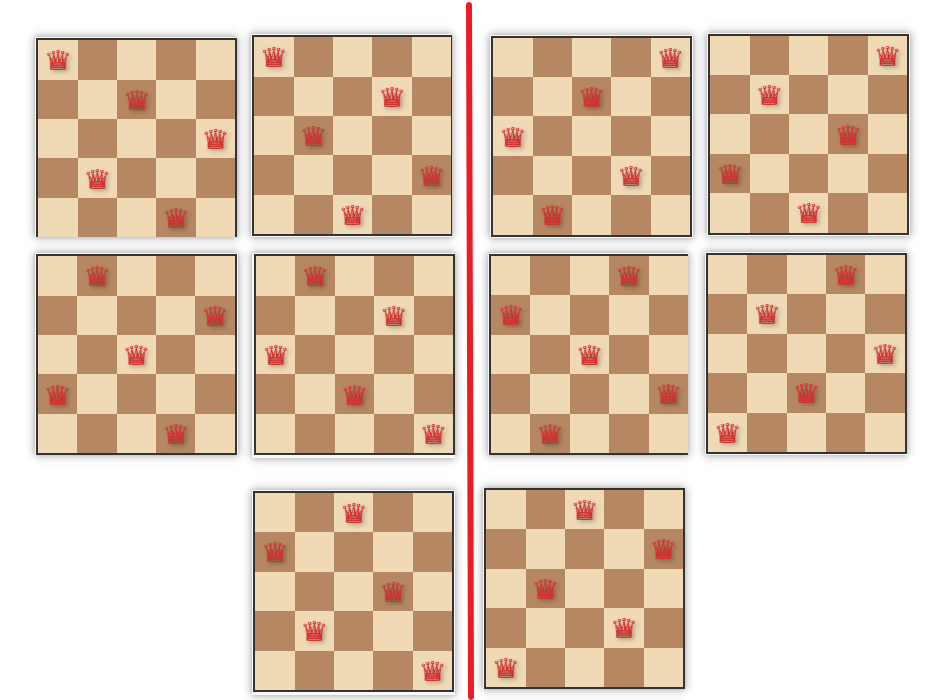
当n=6时，有4种解决方案。
当n=7时，共有40种解。
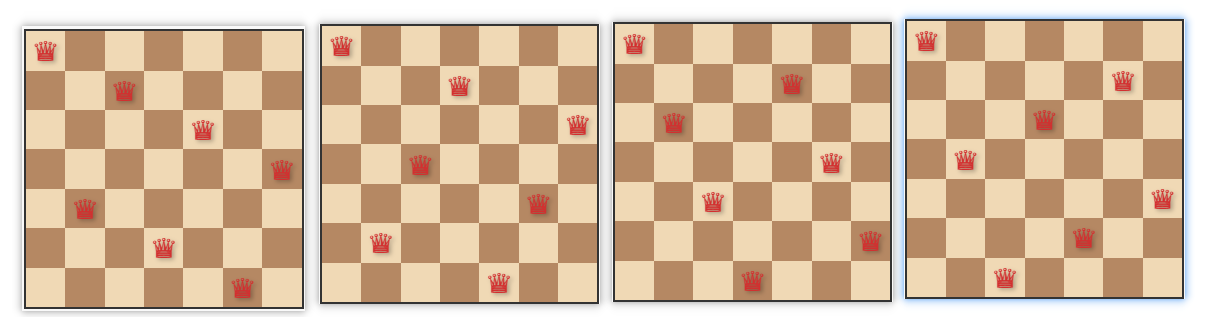当n=8时，共有92种解。
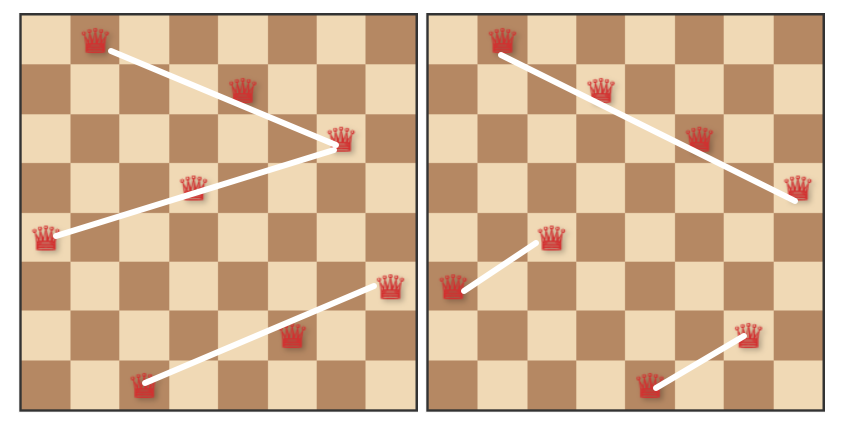
可能 题源9 A∗A^{*}A∗算法
1、A∗A^{*}A∗算法在最短路径中的应用
改进传统的DijkstraDijkstraDijkstra算法，使其在保证最优性的同时大幅度减少计算量。关键在于引入了启发式函数h(n)h(n)h(n)，预估当前节点到终点的代价，优先扩展最有希望的路径。
启发：从某个位置开始找路的时候，利用一些已知信息估算每种选择的代价，然后选择代价最小 的方向。估算代价的函数如下：
f(n)=g(n)+h(n) f(n) = g(n) + h(n) f(n)=g(n)+h(n)
g(n)g(n)g(n)节点nnn距离起点的代价；h(n)h(n)h(n)节点nnn距离终点的预计代价。
若h(n)=0h(n)=0h(n)=0，退化为DijkstraDijkstraDijkstra算法；
若h(n)h(n)h(n)始终小于等于节点nnn到终点的代价，则A∗A^{*}A∗算法一定能找到最短路径；
若h(n)h(n)h(n)的值比节点nnn到终点的代价要大，则A∗A^{*}A∗算法不能保证找到最短路径，但很很快结束。
数如下：
f(n)=g(n)+h(n) f(n) = g(n) + h(n) f(n)=g(n)+h(n)
g(n)g(n)g(n)节点nnn距离起点的代价；h(n)h(n)h(n)节点nnn距离终点的预计代价。
若h(n)=0h(n)=0h(n)=0，退化为DijkstraDijkstraDijkstra算法；
若h(n)h(n)h(n)始终小于等于节点nnn到终点的代价，则A∗A^{*}A∗算法一定能找到最短路径；
若h(n)h(n)h(n)的值比节点nnn到终点的代价要大，则A∗A^{*}A∗算法不能保证找到最短路径，但很很快结束。