目录
[动量法 是什么?](#动量法 是什么?)
[1. 基础梯度下降回顾](#1. 基础梯度下降回顾)
[2. 引入动量项](#2. 引入动量项)
[3. 物理意义与优势](#3. 物理意义与优势)
扩展:NAG (Nesterov Accelerated Gradient)
有小伙伴在学优化算法时问,梯度下降已经有了随机版本,为什么还需要动量法?
它到底解决了什么问题?
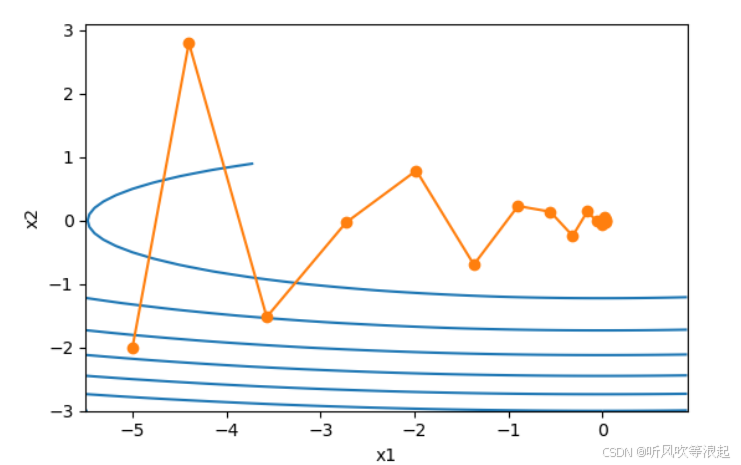
今天,我们就来深入聊聊 动量法(Momentum),看看它是如何让梯度下降变得更"聪明"、更稳定的。
首先,动量法是一种在梯度下降基础上引入"惯性"思想的优化算法。它的目标是加速收敛,并减少优化过程中的振荡,让参数更新更加平滑。
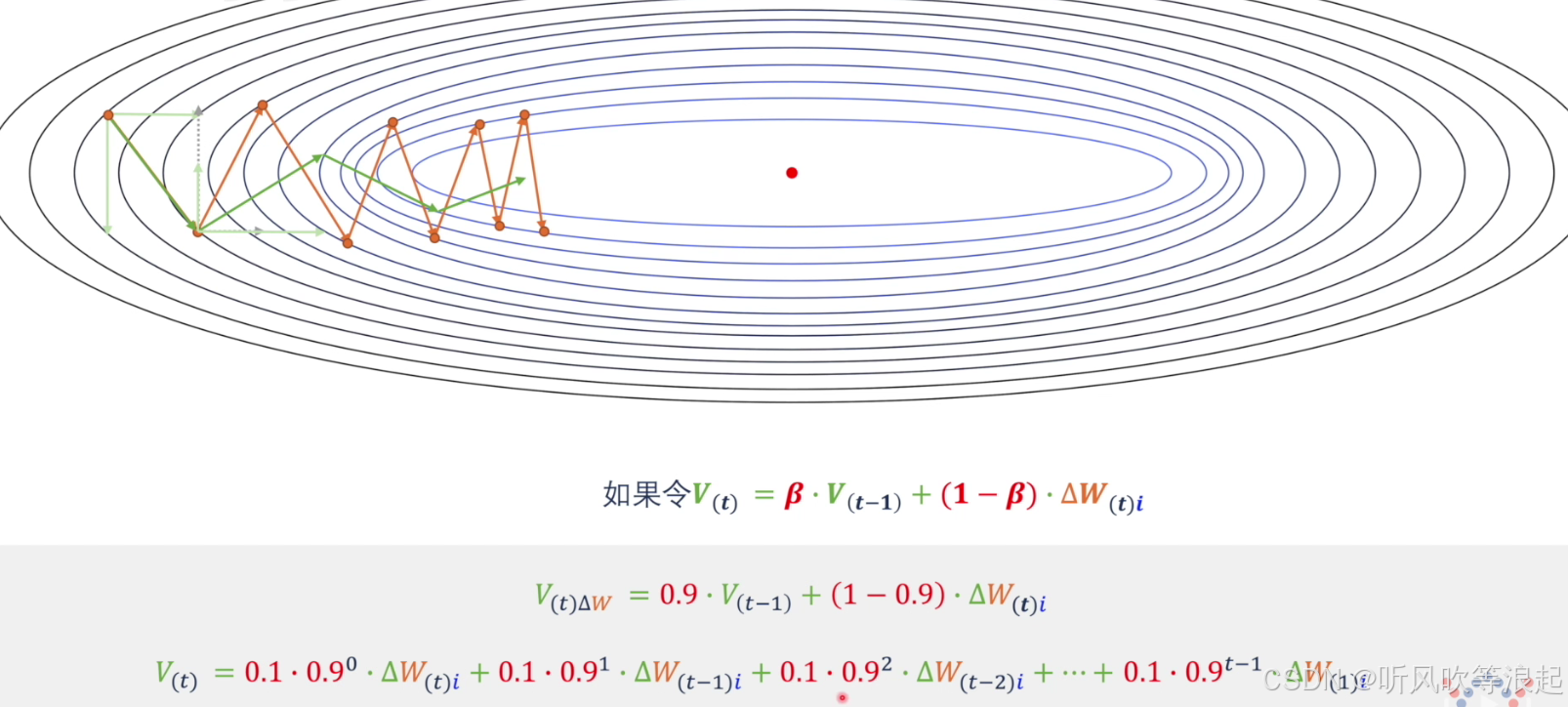
下面,我们从一个生活化的比喻开始,逐步展开。
动量法 是什么?
想象你在下山,目标是尽快到达山谷最低处。
普通的下山方式是:看眼前最陡的方向,直接迈一步。
- 普通梯度下降(GD/SGD): 就像每走一步都重新判断方向。如果地面坑洼不平(梯度有噪声),你的路径就会左摇右摆,走得很慢,甚至可能在沟壑里来回震荡。
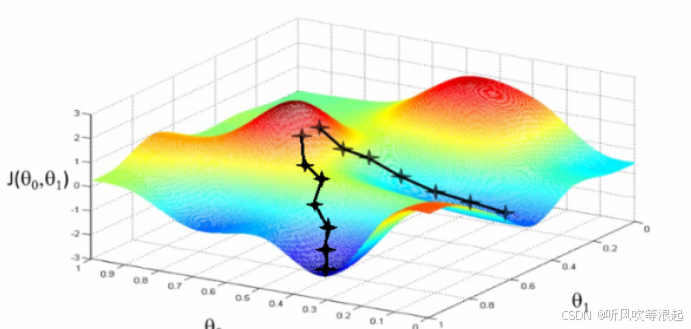
- 动量法(Momentum): 给你一个带轮子的滑板。你当前要前进的方向,不仅由这一步看到的坡度决定,还会受到之前速度(动量)的影响。这样,在平缓地带你会加速,遇到反向坡度时,惯性也能帮你冲过去一部分,减少摆动,整体路径更平滑、更快地指向山谷。
从数学上理解
动量法旨在最小化目标函数 L(θ),其更新规则在梯度下降的基础上增加了动量项:
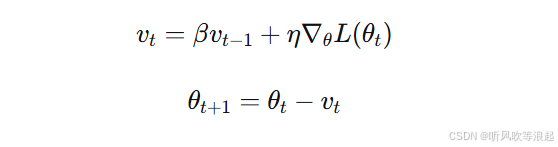
-
θ:模型参数。
-
∇θL(θt):当前时刻的梯度。
-
η:学习率,控制当前梯度的影响。
-
β:动量系数(通常取0.9左右),控制历史动量(速度)的保留比例。
-
vt:当前时刻的更新速度,它累积了历史梯度的方向。
核心思想:当前的更新方向是"历史方向"与"当前梯度方向"的加权组合。这有助于在梯度方向连续一致的方向上加速,在梯度方向频繁变化的方向上抑制振荡。
案例:寻找最佳学习节奏
假设你在调整学习计划中"每日做题数"和"每日复习小时数"两个参数,目标是让学习效率最高。效率损失函数为:
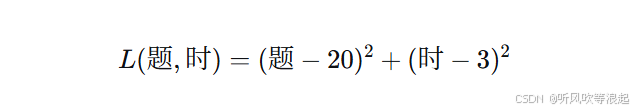
理想状态是 题=20, 时=3,此时损失最小。
模拟计算(对比SGD和动量法)
为了对比,我们先看SGD的更新过程(学习率 η=0.1η=0.1):
-
初始化:题 = 5, 时 = 1。
-
计算梯度:∂L∂题=2(5−20)=−30∂题∂L=2(5−20)=−30,∂L∂时=2(1−3)=−4∂时∂L=2(1−3)=−4。
-
SGD更新:题 = 5 - 0.1*(-30) = 8.0, 时 = 1 - 0.1*(-4) = 1.4。
接下来,我们使用动量法(设 β=0.9,η=0.1β=0.9,η=0.1):
-
初始化参数:题 = 5, 时 = 1。
初始化速度:v题=0,v时=0v题=0,v时=0。
-
计算当前梯度(同上):g题=−30,g时=−4g题=−30,g时=−4。
-
更新速度:
v题=0.9∗0+0.1∗(−30)=−3.0v题=0.9∗0+0.1∗(−30)=−3.0
v时=0.9∗0+0.1∗(−4)=−0.4v时=0.9∗0+0.1∗(−4)=−0.4
-
更新参数:
题 = 5 - (-3.0) = 8.0
时 = 1 - (-0.4) = 1.4
第一步结果看似与SGD相同,因为初始速度为0。
进行第二步 迭代:
当前参数:题=8.0, 时=1.4。
-
计算新梯度:
g题=2(8.0−20)=−24.0g题=2(8.0−20)=−24.0
g时=2(1.4−3)=−3.2g时=2(1.4−3)=−3.2
-
SGD更新:题 = 8.0 - 0.1*(-24) = 10.4, 时 = 1.4 - 0.1*(-3.2) = 1.72。
-
动量法更新速度 :
v题=0.9∗(−3.0)+0.1∗(−24.0)=−2.7−2.4=−5.1v题=0.9∗(−3.0)+0.1∗(−24.0)=−2.7−2.4=−5.1
v时=0.9∗(−0.4)+0.1∗(−3.2)=−0.36−0.32=−0.68v时=0.9∗(−0.4)+0.1∗(−3.2)=−0.36−0.32=−0.68
-
动量法更新参数 :
题 = 8.0 - (-5.1) = 13.1
时 = 1.4 - (-0.68) = 2.08
对比可见:在第二步,动量法由于累积了第一步的梯度(速度-3.0),在参数"题"上的更新幅度(-5.1)远大于SGD的更新幅度(-2.4),从而更快地朝着最优值20靠近。这就是"动量"带来的加速效果。
公式推导与解析
1. 基础梯度下降回顾
标准梯度下降更新: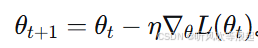
它只考虑当前时刻的梯度。
2. 引入动量项
为了模拟物理中的动量,我们引入速度变量 vt,其更新是指数移动平均:
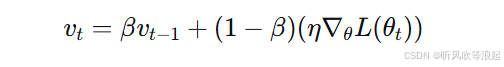
为了简化并与常见形式一致,令 α=η,并将(1−β)吸收进学习率或直接采用另一种常见表述:
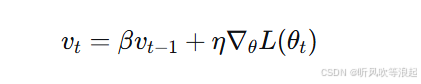
参数更新为: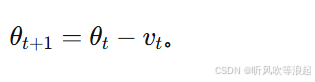
3. 物理意义与优势
将 vt 展开:
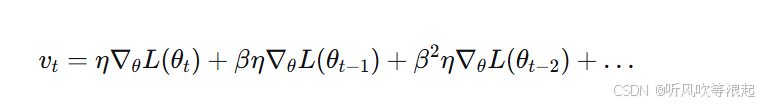
更新方向是当前梯度与历史梯度的加权和。越近的梯度权重越大。
-
加速收敛:在损失函数曲面在某个方向持续下降(梯度方向一致)时,动量会不断累积,更新速度越来越快。
-
抑制振荡:在梯度方向变化频繁(如峡谷形曲面)的方向上,正负梯度会部分抵消,使得更新幅度变小,路径更稳定。
扩展:NAG (Nesterov Accelerated Gradient)
动量法的一个改进版本是NAG,它"向前看"一步:
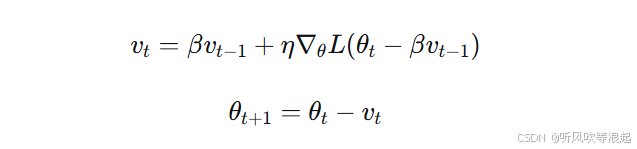
NAG先根据累积速度"预览"下一步的参数位置,然后计算该预览位置的梯度,再进行更新。
这使得它在面对即将变化的梯度时能更早地做出调整,理论上有更好的收敛性。

优缺点和适用场景
优点
-
加速收敛:在目标函数呈狭长峡谷状或存在平缓区域时,能显著加快训练速度。
-
减少振荡:平滑优化路径,使训练过程更稳定,有助于使用更大的学习率。
-
有助于跳出局部极小:动量带来的"惯性"可能帮助参数冲过一些狭窄的局部极小点。
缺点
-
引入超参数:需要调整动量系数 β,通常为0.9,但最优值可能因问题而异。
-
可能 overshooting:在极陡的梯度面前,过大的动量可能导致更新过头,在最优值附近震荡甚至发散。
适用场景
-
高维非凸优化:如深度学习,特别是网络层数较深时。
-
梯度噪声较大或方向不一致:当数据存在噪声或Mini-batch较小时,动量能起到平滑作用。
-
追求更快的训练速度:在资源有限的情况下,希望用更少的迭代次数达到可接受的损失。
完整代码示例:在回归问题中对比SGD与动量法
下面我们用一个简单的线性回归问题,来可视化对比普通SGD和带动量的SGD的优化轨迹。
python
import numpy as np
import matplotlib.pyplot as plt
# 1. 生成模拟数据
np.random.seed(42)
# 真实参数:w_true = 2.5, b_true = 1.0
X = 2 * np.random.rand(100, 1)
y = 2.5 * X + 1.0 + np.random.randn(100, 1) * 0.5 # 添加噪声
# 2. 定义损失函数(均方误差)和梯度
def compute_gradients(X, y, w, b):
m = len(X)
y_pred = X * w + b
dw = (-2/m) * np.sum(X * (y - y_pred))
db = (-2/m) * np.sum(y - y_pred)
return dw, db
# 3. 定义优化器
def sgd_optimizer(w, b, dw, db, lr):
w_new = w - lr * dw
b_new = b - lr * db
return w_new, b_new
def momentum_optimizer(w, b, dw, db, lr, beta, v_w, v_b):
v_w = beta * v_w + lr * dw
v_b = beta * v_b + lr * db
w_new = w - v_w
b_new = b - v_b
return w_new, b_new, v_w, v_b
# 4. 训练参数设置
lr = 0.1
beta = 0.9
n_iterations = 50
# 初始化参数(两者起点相同)
w_sgd, b_sgd = np.random.randn(2) * 5 # 随机初始化
w_mom, b_mom = w_sgd, b_sgd
v_w, v_b = 0, 0 # 动量速度初始化为0
# 用于记录轨迹
path_sgd = [(w_sgd, b_sgd)]
path_mom = [(w_mom, b_mom)]
# 5. 执行训练
for i in range(n_iterations):
# 计算梯度(使用全量数据简化演示)
dw, db = compute_gradients(X, y, w_sgd, b_sgd)
# SGD 更新
w_sgd, b_sgd = sgd_optimizer(w_sgd, b_sgd, dw, db, lr)
path_sgd.append((w_sgd, b_sgd))
# 动量法更新 (需要重新计算当前参数的梯度)
dw_m, db_m = compute_gradients(X, y, w_mom, b_mom)
w_mom, b_mom, v_w, v_b = momentum_optimizer(w_mom, b_mom, dw_m, db_m, lr, beta, v_w, v_b)
path_mom.append((w_mom, b_mom))
# 转换为数组方便绘图
path_sgd = np.array(path_sgd)
path_mom = np.array(path_mom)
# 6. 可视化优化轨迹
plt.figure(figsize=(12, 5))
# 子图1:参数空间轨迹
plt.subplot(1, 2, 1)
# 绘制损失函数等高线(近似)
W_grid, B_grid = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
Loss = np.zeros_like(W_grid)
for i in range(W_grid.shape[0]):
for j in range(W_grid.shape[1]):
Loss[i,j] = np.mean((y - X * W_grid[i,j] - B_grid[i,j])**2)
plt.contour(W_grid, B_grid, Loss, levels=30, alpha=0.5)
plt.scatter(2.5, 1.0, c='red', s=100, marker='*', label='True Optimum (w=2.5, b=1.0)')
plt.plot(path_sgd[:,0], path_sgd[:,1], 'o-', label='SGD Path', linewidth=2, markersize=4)
plt.plot(path_mom[:,0], path_mom[:,1], 's-', label='Momentum Path', linewidth=2, markersize=4)
plt.xlabel('Weight (w)')
plt.ylabel('Bias (b)')
plt.title('Optimization Path in Parameter Space')
plt.legend()
plt.grid(True, alpha=0.3)
# 子图2:损失下降曲线
plt.subplot(1, 2, 2)
loss_sgd = [np.mean((y - X * w - b)**2) for w, b in path_sgd]
loss_mom = [np.mean((y - X * w - b)**2) for w, b in path_mom]
plt.plot(range(len(loss_sgd)), loss_sgd, label='SGD Loss')
plt.plot(range(len(loss_mom)), loss_mom, label='Momentum Loss')
plt.xlabel('Iteration')
plt.ylabel('Mean Squared Error Loss')
plt.title('Loss Convergence Curve')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()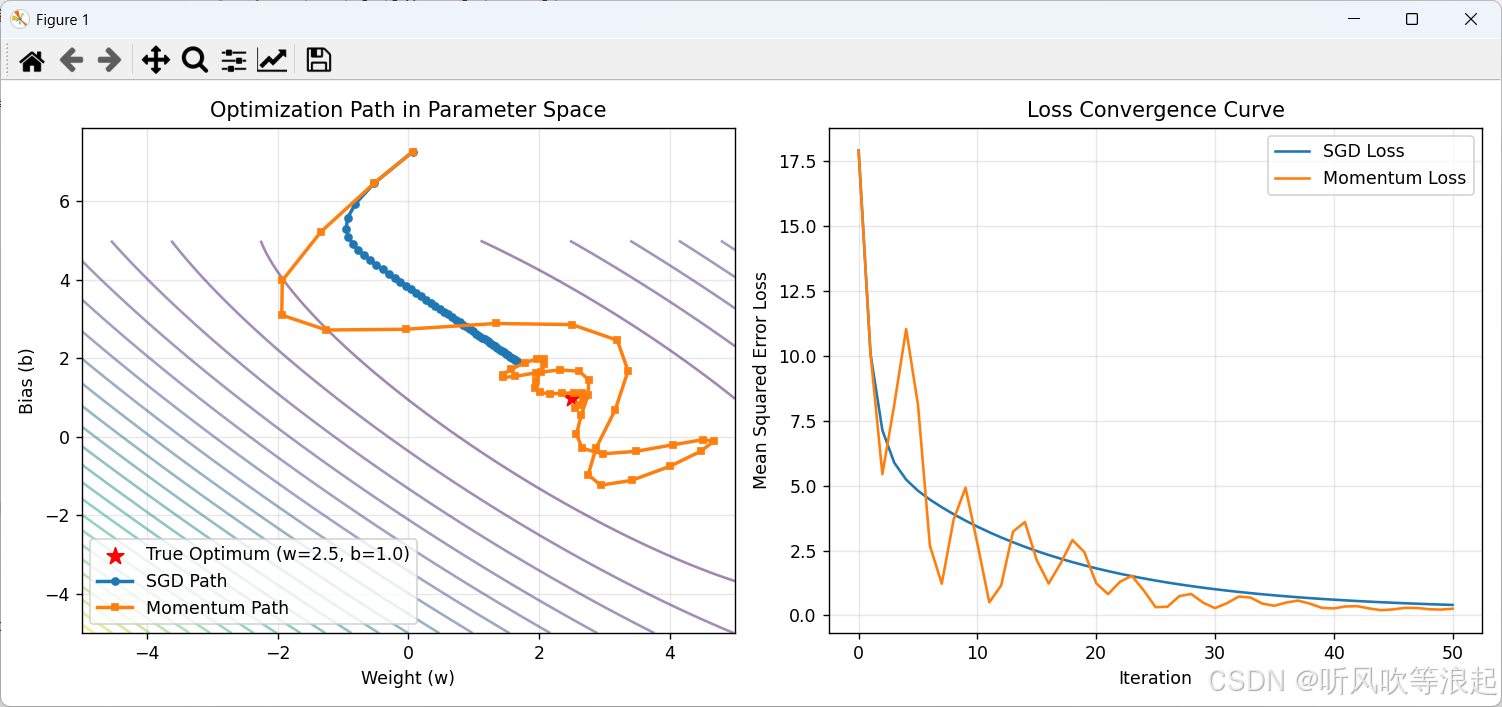
代码说明与结果解读:
-
左图(参数空间轨迹):
-
背景等高线代表损失函数值,中心红五星为全局最优点。
-
SGD(圆点线) 的更新路径曲折,呈"锯齿状"缓慢靠近最优点。
-
动量法(方块线) 的路径明显更加平滑、直接,更快地指向最优点,体现了动量在一致梯度方向上的加速效果。
-
-
右图(损失下降曲线):
- 动量法(橙色)的损失值下降速度整体快于普通SGD(蓝色),尤其是在初期,收敛更快。
通过这个对比实验,可以直观地看到动量法如何优化梯度下降的过程,使其更高效、更稳定