统计学不研究统计,研究概率!!!
最近在工作中遇到了需要数据分析的工作,下面对数据分析中遇到的一些统计学知识点进行总结。
eg1 首先,分析一张数据表时,先对表中的各特征用柱状图、折线图大致看一下数据的分布情况,比如说在分析正常电芯和异常电芯在N个特征上有何不同时,可以用正常电芯的各项特征均值代表正常电芯的整体水平,由于异常电芯数量较少,所以可以全部展示出来在每个特征它们的概况。
将这张表送入模型时,在这过程中会遇到一些缺失值,需要对缺失值处理 ;为了展示模型的效果通常还需要将这些数据对比展示在同一个图中,但这些特征来自不同的"视角",因此它们的单位都不同,为了公平起见,需要对他们统一量纲;
eg2 为了在大量数据中更有效的分析出异常点,可以要从众多角度对比,这就必须清晰各个数据基本变化代表的含义 ,如果从这些基本变化上还是区分不出,还有两条路,一是交给ML,另一条是用基于统计学的异常检测。
数据分析 Part 1
- 数据基本变化及意义
- [🌟 1、数据基本变化及意义](#🌟 1、数据基本变化及意义)
- [🌟 2、基于统计学的异常值检测技术](#🌟 2、基于统计学的异常值检测技术)
- [🌟 3、消除量纲的方法](#🌟 3、消除量纲的方法)
- [🌟 4、缺失值处理方法](#🌟 4、缺失值处理方法)
- 🌟5、特征分析
数据基本变化及意义
二级目录
🌟 1、数据基本变化及意义
数据画像




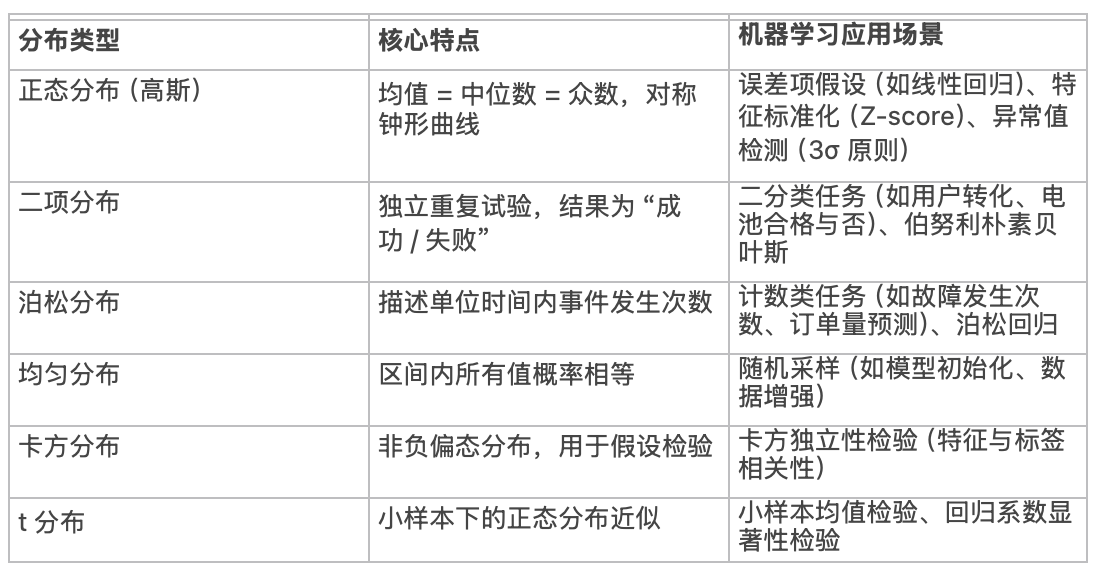
概率模型与ML场景
马尔可夫、隐式马尔可夫
可视化
1、箱线图
🌟 2、基于统计学的异常值检测技术
1、单变量正态分布(3sigma原则)


2、单变量偏态分布(IQR)---用箱线图可视化
无需假设数据分布(非参数方法),基于四分位数描述数据的 "集中范围"
IQR = Q3-Q1
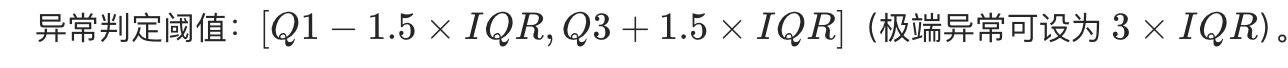
3、马氏距离(多变量分布)

4、高斯混合(GMM)

5、局部异常因子(LOF)


6、孤立森林(IF)

7、K-NN

按需选择
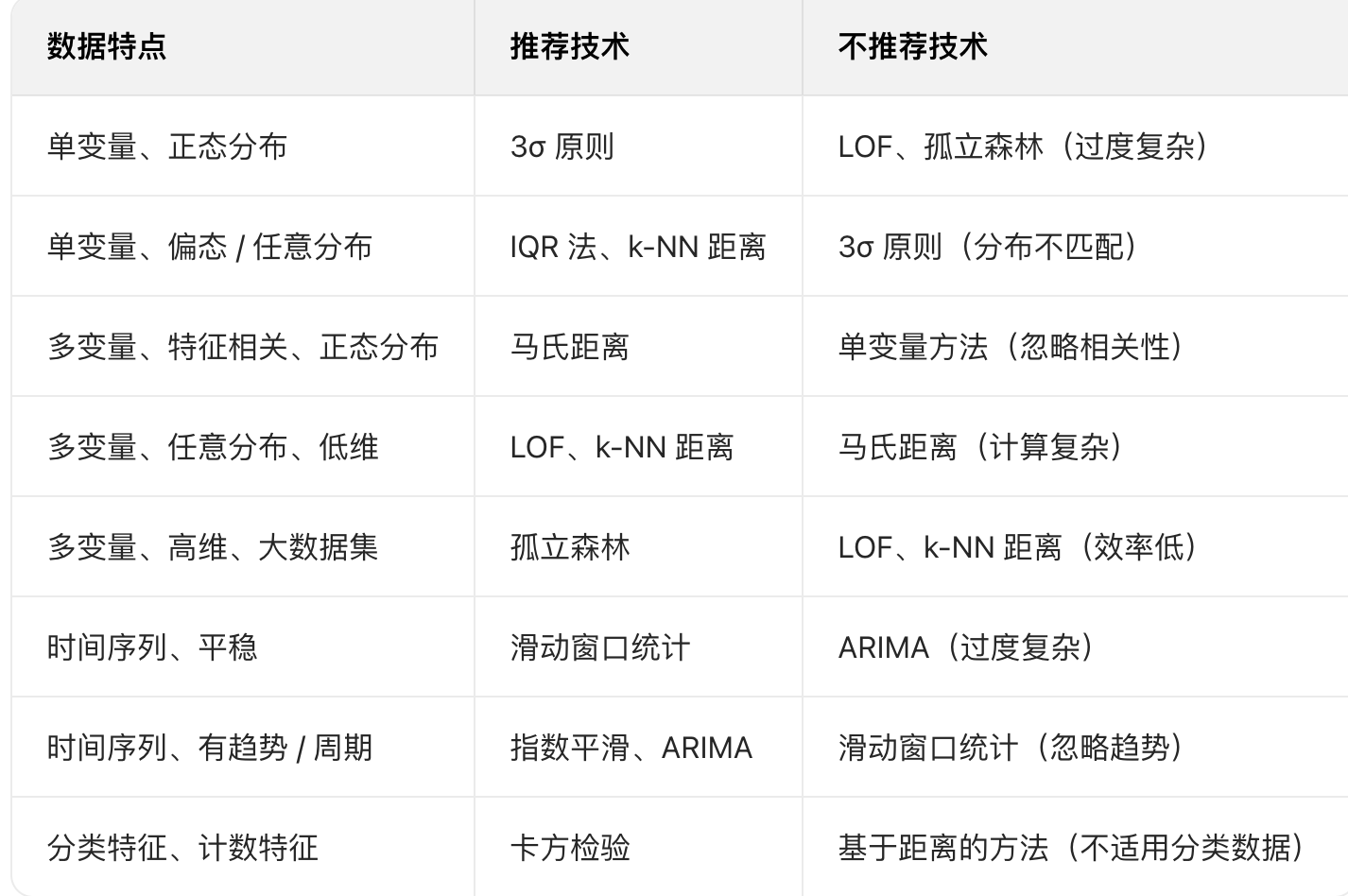
- 简单场景(单变量、分布明确):优先用 3σ、1.5 IQR 法;
- 复杂场景(多变量、高维、任意分布):优先用孤立森林、LOF;
- 时间序列场景:优先用滑动窗口、指数平滑、ARIMA
统计学异常检测技术的核心优势是无需标注、解释性强、计算高效,复杂方法(如 LOF、孤立森林)可结合可视化(如散点图、箱线图)辅助解释异常原因
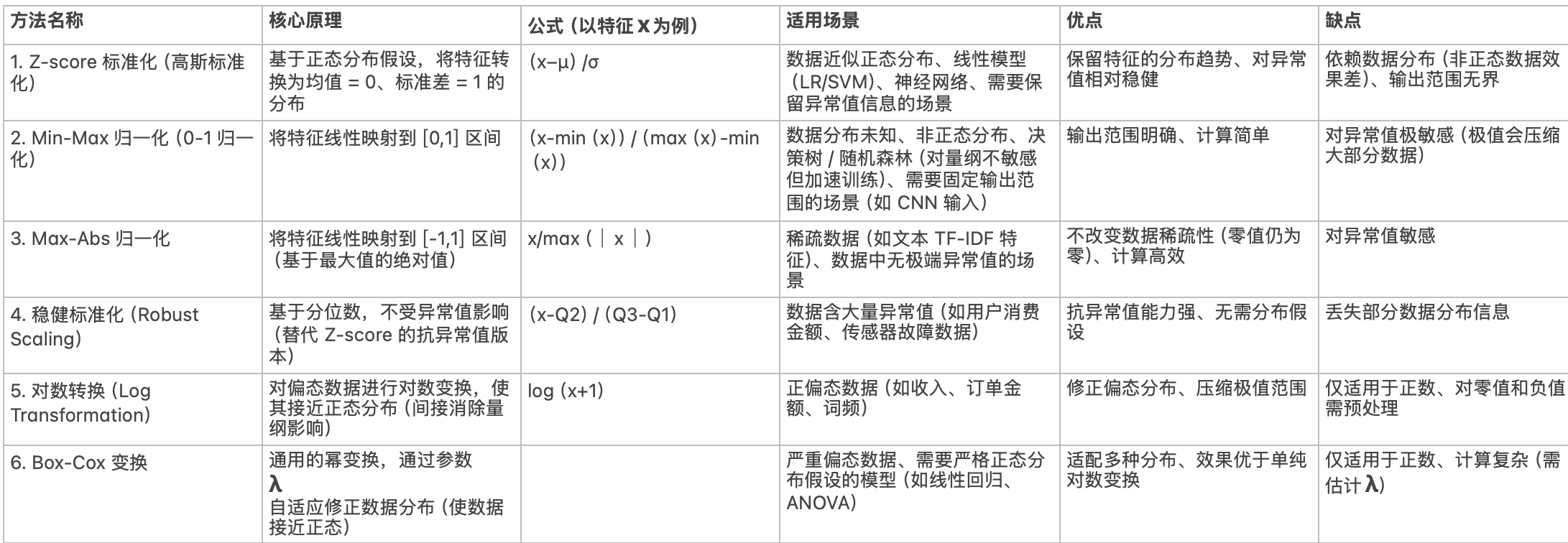
🌟 3、消除量纲的方法
多变量方法(如马氏距离、LOF)需标准化(消除量纲),单变量方法(如 IQR、3σ)无需标准化
1、Z分数法:基于正态分布假设,适用于线性回归、SVM、神经网络
2、归一化:适用于均匀分布数据、决策树(对量纲不敏感,但归一化可加速训练)
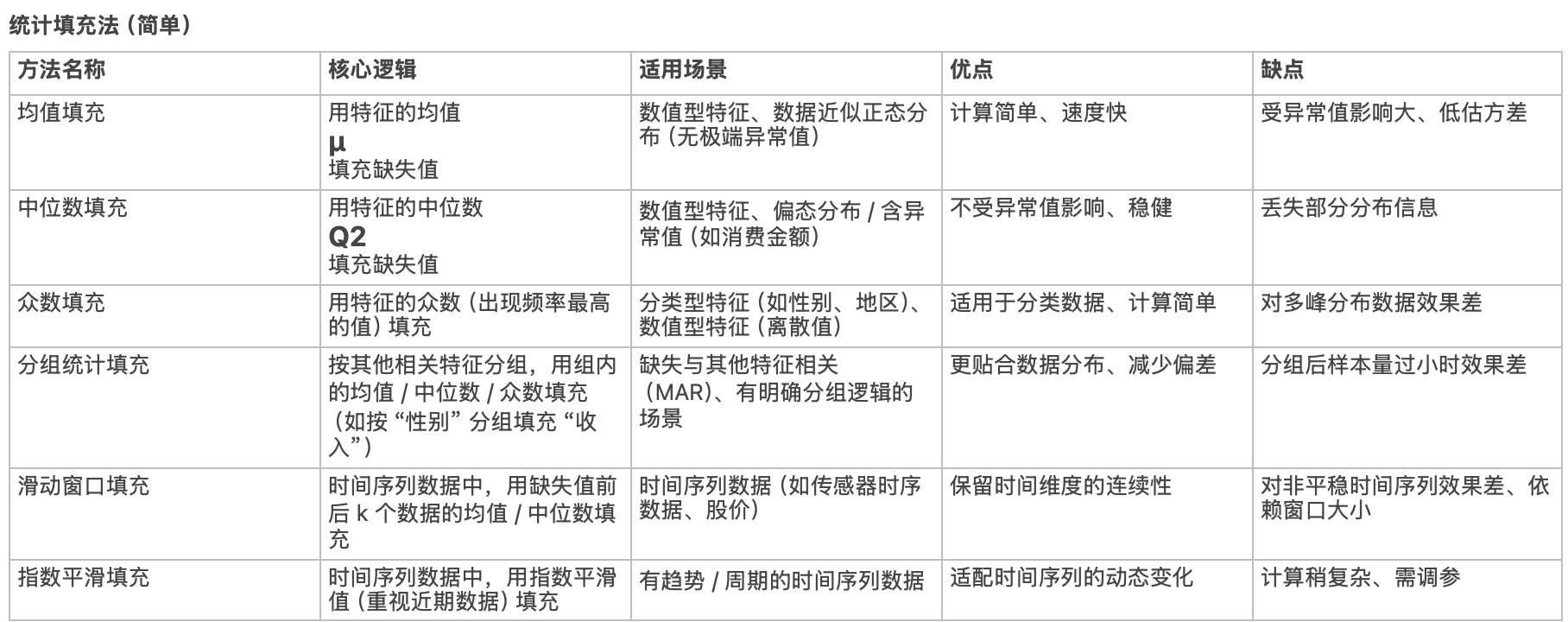
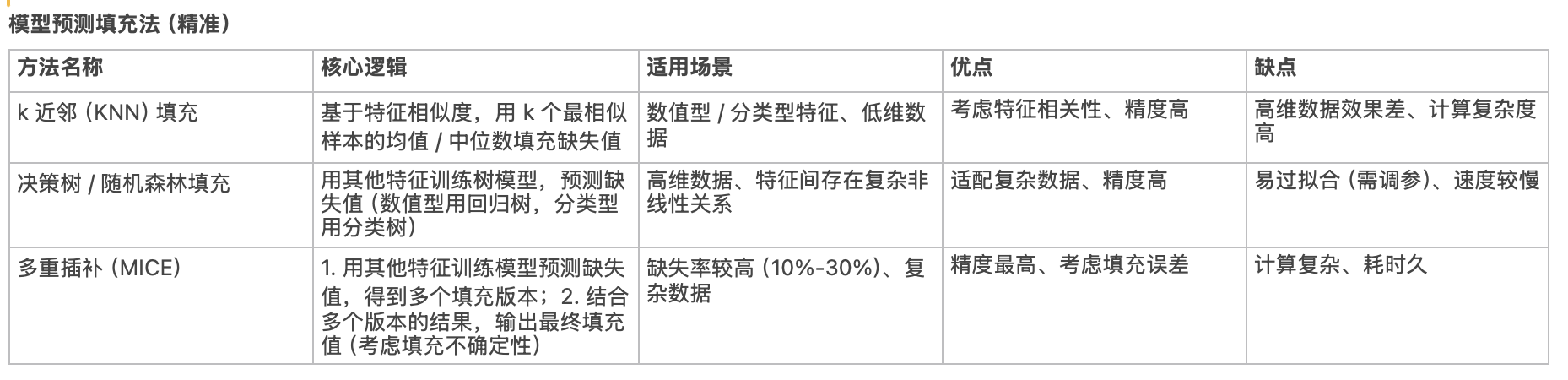
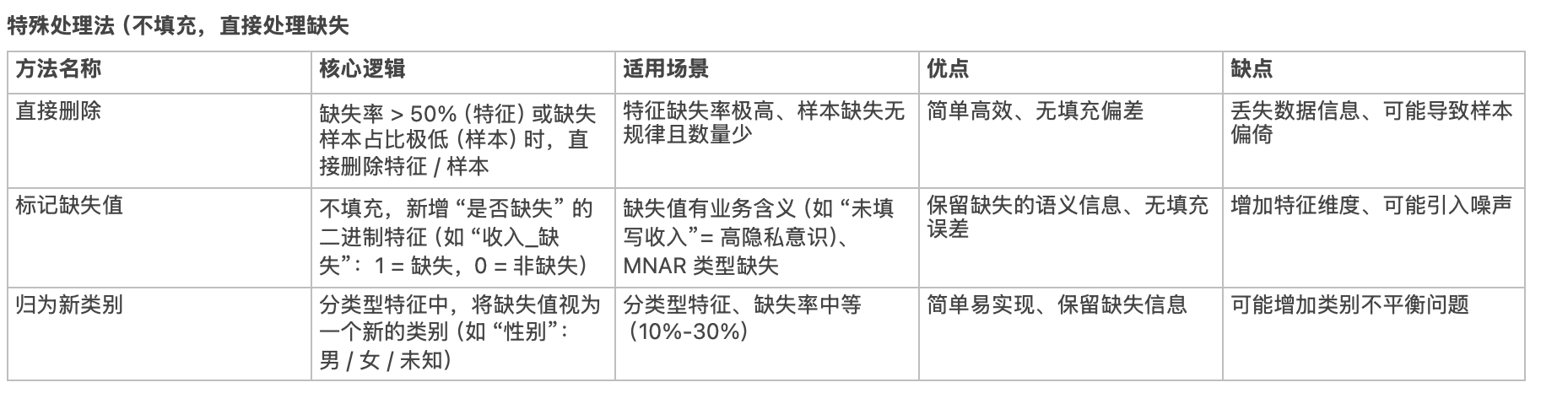
🌟 4、缺失值处理方法
- 统计缺失率:若缺失率 > 50%,直接删除特征;否则根据数据类型填充(数值型:均值 / 中位数 / 众数 / KNN 填充;分类型:众数 / 模型预测填充)
- 异常值:3σ 原则(正态分布)、IQR 法(任意分布)、Z-score(标准化后异常值 Z>3 或 Z<-3)
- 异常值处理方式:删除(异常值少且无意义)、修正(如录入错误)、保留(可能是有效信号,如异常电芯)
🌟5、特征分析
相关性分析
可以用来去除冗余特征
- 皮尔逊相关系数(Pearson)
衡量线性相关(数值型数据)→ 取值 [-1,1],绝对值越大相关性越强(r=1 完全正相关,r=-1 完全负相关,r=0 无线性相关) - 斯皮尔曼等级相关(Spearman)
衡量单调相关(有序分类 / 数值型)→ 基于数据排名,不受异常值影响(如用户满意度与消费金额的非线性单调关系) - 肯德尔相关(Kendall)
衡量一致性(适用于小样本、有序数据) - 分类数据相关性
卡方检验(χ²)→ 检验特征与标签是否独立(如 "性别" 与 "是否购买" 的关联)
重要度分析
解释特征对模型结果的贡献度
- 方差分析(ANOVA):检验不同类别下特征的均值是否有显著差异(F 统计量)→ 用于分类任务的特征筛选(F 值越大,特征区分度越强)
- 互信息(Mutual Information):衡量特征与标签的非线性关联→ 弥补相关系数的不足(如决策树、随机森林的特征重要性基础)
重要性可视化
SHAP、Waterfall
SHAP 负责计算 "特征贡献度",Waterfall 负责把 "贡献度" 以 "流水账" 的形式画出来
- SHAP:最强大的模型可解释性框架之一,核心是 "归因"------ 量化每个特征对预测结果的贡献。
- Waterfall:是 SHAP 提供的可视化方式

