空间直线方程

空间直线的方向向量

直线上任意两点的坐标差就是该直线的方向向量，用二维空间很容易表示出来。

先看以下图：

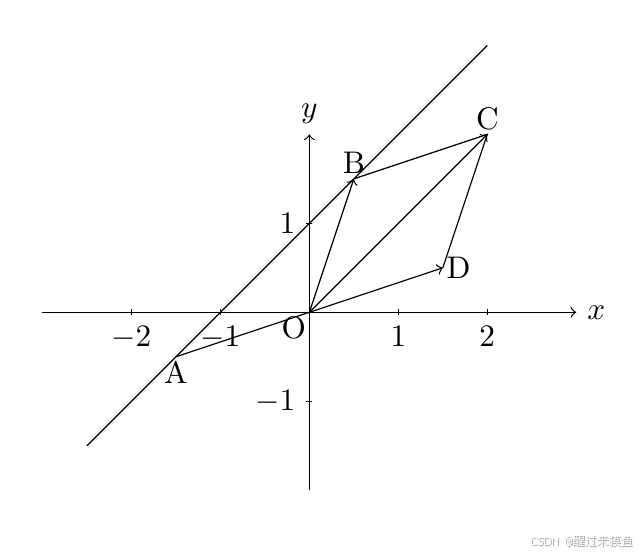
图中AB是直线上任意两点，OA和OB则是这两点表示的的向量，OD是OA反方向等长的，所以AB两点的坐标差就相当于 O B → + O D → \overrightarrow{OB}+\overrightarrow{OD} OB +OD ，根据平行四边形法则就是 O C → \overrightarrow{OC} OC .因为 B C ‾ = O D ‾ = O A ‾ \overline{BC}=\overline{OD}=\overline{OA} BC=OD=OA且BC平行于AD这条直线，所以OABC是一个平行四边形。那么OC就平行与AB所在的直线，所以直线上AB两点坐标差就是直线的方向向量 O C → \overrightarrow{OC} OC 。

该图绘图代码为:

latex 复制代码

\documentclass{article}
\usepackage{tikz}
\begin{document}
	\begin{tikzpicture}
	
			% 定义绘图范围
			\draw[->] (-3,0) -- (3,0) node[right] {$x$}; % x 轴
			\draw[->] (0,-2) -- (0,2) node[above] {$y$}; % y 轴
			
			% 添加刻度
			\foreach \x in {-2,-1,1,2}
			\draw (\x cm,1pt) -- (\x cm,-1pt) node[anchor=north] {$\x$};
			\foreach \y in {-1,1}
			\draw (1pt,\y cm) -- (-1pt,\y cm) node[anchor=east] {$\y$};
			\coordinate (A1) at (-2.5, -1.5);
			\coordinate (A) at (-1.5, -0.5);
			\coordinate (B) at (0.5, 1.5);
			\coordinate (B1) at (2.0, 3.0);
			\coordinate (C) at (2, 2);
			\coordinate (D) at (1.5, 0.5);
			\coordinate (O) at (0, 0);
			
			\node[yshift=-5pt] at (A) {A};
			\node[yshift=5pt] at (B) {B};
			\node[yshift=5pt] at (C) {C};
			\node[xshift=5pt] at (D) {D};
			\node[xshift=-5pt,yshift=-5pt] at (O) {O};
			\draw[->] (A)  -> (D);
			\draw (D) --(C) -- (B) ;
			\draw (A1) -- (B1);
			\draw[->] (O)  -> (B);
			\draw[->] (O)  -> (C);
	\end{tikzpicture}
\end{document}

空间直线的对称式方程

假设空间直线经过一个点 A 0 A_0 A0，坐标为 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)，且有一个方向向量为(m,n,p)，那么根据上述结论，直线上任意一点 ( x , y , z ) (x,y,z) (x,y,z)和 A 0 A_0 A0的坐标差与方向向量就有坐标比例关系，那么就有：
x − x 0 = t m y − y 0 = t n z − z 0 = t p ⟹ x − x 0 m = y − y 0 n = z − z 0 p = t x-x_0=tm\\ y-y_0=tn\\ z-z_0=tp\\ \implies \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t x−x0=tmy−y0=tnz−z0=tp⟹mx−x0=ny−y0=pz−z0=t

这就是直线的对称式方程，也叫点向式方程。同时也容易得到参数方程：
x = t m + x 0 y = t n + y 0 z = t p + z 0 x=tm+x_0\\ y=tn+y_0\\ z=tp+z_0 x=tm+x0y=tn+y0z=tp+z0

直线的夹角

直线的夹角 θ \theta θ，用方向向量的2-范数很容易求出来了。假设两个方向向量是 v 1 , v 2 \bm{v_1} , \bm{v_2} v1,v2，就可以用下面的公式了：
cos ⁡ ( θ ) = ∣ v 1 ⋅ v 2 ∣ ∥ v 1 ∥ 2 ∥ v 2 ∥ 2 \cos(\theta)=\frac{|\bm{v_1} \cdot \bm{v_2}|}{\lVert \bm{v_1} \rVert_2\lVert \bm{v_2} \rVert_2} cos(θ)=∥v1∥2∥v2∥2∣v1⋅v2∣

这里加上绝对值是为了把钝角变成锐角,所以和线性代数里不加绝对值的公式不同。

直线与平面的夹角

对于一般的平面 a x + b y + c z = d ax+by+cz=d ax+by+cz=d，其中一个法向量就是 ( a , b , c ) (a,b,c) (a,b,c)。至于为什么，可以取平面上任意两点就可以了。假设有两点 A 1 ( x 1 , y 1 , z 1 ) , A 2 ( x 2 , y 2 , z 2 ) A_1(x_1,y_1,z_1),A_2(x_2,y_2,z_2) A1(x1,y1,z1),A2(x2,y2,z2)在该平面上，那么两点的坐标差就是这两点的方向向量 ( x 1 − x 2 , y 1 − y 2 , z 1 − z 2 ) (x_1-x_2,y_1-y_2,z_1-z_2) (x1−x2,y1−y2,z1−z2)，该方向向量和 ( a , b , c ) (a,b,c) (a,b,c)的内积为：
a ( x 1 − x 2 ) + b ( y 1 − y 2 ) + c ( z 1 − z 2 ) = a x 1 + b y 1 + c z 1 − a x 2 − b y 2 − c z 2 = d − d = 0 a(x_1-x_2)+b(y_1-y_2)+c(z_1-z_2)\\ =ax_1+by_1+cz_1-ax_2-by_2-cz_2\\ =d-d=0 a(x1−x2)+b(y1−y2)+c(z1−z2)=ax1+by1+cz1−ax2−by2−cz2=d−d=0

所以平面上任意两点的方向向量都垂直于 ( a , b , c ) (a,b,c) (a,b,c)这个向量，那毫无疑问是法向量了。

那么直线和平面的夹角 θ \theta θ,假设直线的方向向量是 v 1 \bm{v_1} v1，平面的法向量是 v 2 \bm{v_2} v2,夹角 θ \theta θ就可以按下面公式求了：
sin ⁡ ( θ ) = ∣ v 1 ⋅ v 2 ∣ ∥ v 1 ∥ 2 ∥ v 2 ∥ 2 \sin(\theta)=\frac{|\bm{v_1} \cdot \bm{v_2}|}{\lVert \bm{v_1} \rVert_2\lVert \bm{v_2} \rVert_2} sin(θ)=∥v1∥2∥v2∥2∣v1⋅v2∣