别再迷信“准确率”了！一文读懂 AI 图像分割的黄金标尺 —— Dice 系数

1. 引言：99% 的准确率，可能意味着模型是个"废物"？

想象这样一个痛点场景：

你正在训练一个 AI 模型，任务是从脑部核磁共振（MRI）扫描中找出极小的肿瘤区域 。你熬夜跑完代码，发现模型在验证集上的 Accuracy（准确率）高达 99.9%！

你兴奋地开了香槟，但当你把预测结果打印出来一看，心凉了半截：模型把整张图都预测成了"黑色背景"，一个肿瘤都没圈出来。

为什么？因为肿瘤只占图像的 0.1%，模型只要"偷懒"全猜背景，准确率就能达到 99.9%。这就是经典的**样本不平衡（Class Imbalance）**问题。单纯的准确率在这里彻底失效了。

解决方案：

今天的主角 Dice 系数（Dice Coefficient）及其衍生出的 Dice Loss，就是为了解决这个问题而生的。它不关心背景有多大，它只关心：你画的圈，和标准答案的圈，重合度到底有多高？

2. 概念拆解：像是两张"剪纸"的重叠游戏

生活化类比：批改填色画

为了理解 Dice，我们忘掉复杂的数学公式，来玩一个填色游戏。

假设老师给了一张画着线条的黑白线稿（原始图片），要求你把其中的"猫"涂红（这是你的预测 Prediction）。老师手里有一张标准答案，猫已经被涂红了（这是真值 Ground Truth）。

评判你画得好不好的标准是 Dice，它的逻辑是这样的：

老师把你的画纸和标准答案叠在一起，对着光看。
重叠部分（Intersection）：两张纸上都涂红了的地方，这是你画对的核心区域。
总面积（Union-ish）：你涂红的总面积 + 老师标准答案涂红的总面积。

Dice 的核心逻辑：

为什么公式里要乘以 2？

这是一个很棒的直觉问题。

分母计算的是（A的面积 + B的面积）。
在这个加法中，重叠的那部分区域其实被加了两次（在 A 里算了一次，在 B 里又算了一次）。
为了让分子和分母在量级上"公平对等"，我们也把分子的重叠面积乘以 2。
这样，当 A 和 B 完全重合时，分子分母相等，Dice = 1（完美）；当完全不重合时，Dice = 0。

Dice Loss 是什么？

在神经网络训练中，我们需要一个"损失函数"（Loss），通过让 Loss 变小来优化模型。

Dice 系数越大越好（最高是1），所以我们定义：

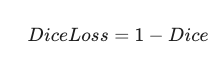
这样，Dice 系数越高，Loss 就越低，模型就越开心。

3. 动手实战：PyTorch 手撸 Dice Loss

光说不练假把式。我们来实现一个生产环境可用的 Dice Loss。

Hello World (MVP 代码)

这是一个基于 PyTorch 的实现。
Python

复制代码

import torch
import torch.nn as nn

class DiceLoss(nn.Module):
    def __init__(self, smooth=1e-5):
        super(DiceLoss, self).__init__()
        self.smooth = smooth  # 防止分母为 0 的平滑项

    def forward(self, predict, target):
        """
        predict: 模型的预测输出 (经过 Sigmoid 或 Softmax)
        target: 真实的标签 (0 或 1)
        """
        # 1. 展平张量 (Flatten)
        # 将 [Batch, Channel, Height, Width] 展平成一维向量，方便计算点积
        predict = predict.view(-1)
        target = target.view(-1)
        
        # 2. 计算交集 (Intersection)
        # 只有当 predict 和 target 对应位置都大时，乘积才大
        intersection = (predict * target).sum()
        
        # 3. 计算各自的面积和 (分母)
        # 直接相加所有像素值
        union = predict.sum() + target.sum()
        
        # 4. 计算 Dice 系数
        dice = (2. * intersection + self.smooth) / (union + self.smooth)
        
        # 5. 返回 Loss (1 - Dice)
        return 1 - dice

# --- 测试一下 ---
# 模拟一张 4x4 的图片
fake_pred = torch.tensor([0.9, 0.1, 0.8, 0.1], dtype=torch.float32) # 模型认为第1、3个像素是目标
fake_target = torch.tensor([1.0, 0.0, 1.0, 0.0], dtype=torch.float32) # 实际上第1、3个像素确实是目标

criterion = DiceLoss()
loss = criterion(fake_pred, fake_target)

print(f"Dice Loss: {loss.item():.4f}") 
# 预期结果非常接近 0，因为预测和标签高度重合

代码深度解析

smooth (平滑项)：
- 为什么需要它？ 如果模型预测全是黑（0），标签也全是黑（0），分母就会变成 0，导致程序崩溃（NaN）。加上一个极小的数（如 1e-5）可以避免除以零。
- 意外收获：它还能防止过拟合，起到一点正则化的作用。
view(-1) (展平)：
- 图像通常是二维或三维的，但计算重叠面积时，我们只关心像素点的"总量"。把它拉成一条直线计算点积（Dot Product），代码更简洁且速度更快。
predict * target：
- 这是一个巧妙的计算"交集"的方法。因为 Target 是 0 或 1：
  - 如果 Target 是 0（背景），不管你预测多少，乘积都是 0。
  - 如果 Target 是 1（目标），乘积就是你的预测信心值（比如 0.9）。
- 这就只保留了目标区域的预测情况。

4. 进阶深潜：新手容易踩的坑

虽然 Dice 很强，但它不是万能的。在实际生产中，你可能会遇到以下问题：

陷阱 1：梯度不稳定 (Gradient Instability)

Dice Loss 的曲线是非常非凸（Non-convex）的。简单说，当模型预测非常离谱（完全没有交集）时，Dice 的梯度可能非常小或非常剧烈，导致训练初期模型很难收敛。

最佳实践：组合拳（Combo Loss）。

通常我们将 Dice Loss 和 Cross Entropy Loss (交叉熵) 结合使用。
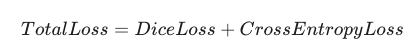
- 交叉熵负责让梯度的方向平滑稳定。
- Dice 负责在细节上精雕细琢，处理样本不平衡。

陷阱 2：激活函数的遗漏

Dice Loss 接收的输入必须是 0 到 1 之间 的概率值。

错误做法：直接把网络的原始输出（Logits，范围可能是负无穷到正无穷）扔进 Dice Loss。
正确做法 ：先过一层 Sigmoid (二分类) 或 Softmax (多分类)，确保值在 [0, 1] 之间，然后再计算 Dice。

陷阱 3：不仅是二分类

上面的代码是针对二分类（目标 vs 背景）的。如果是多分类（比如要把脑部分割成：白质、灰质、脑脊液），你需要：

对预测结果做 One-hot 编码。
分别计算每一个类别的 Dice。
取平均值（Mean Dice）。

5. 总结与延伸

核心总结

Dice 系数 就像是给 AI 戴上了一副"只看目标"的眼镜。它通过计算集合重叠度 ，完美解决了图像分割中背景过大、目标过小 的样本不平衡问题。记住公式的核心：2 倍交集除以总面积。