备战蓝桥杯------双指针基础题型总结
引言
双指针技巧是算法竞赛和面试中的高频考点,其核心在于通过两个指针的协同移动,将许多需要嵌套循环的 O(n²) 问题优化到 O(n) 或 O(n log n)。掌握双指针,能显著提升对数组、链表、字符串等线性数据结构的处理效率。本文将通过一系列经典题目,系统讲解双指针算法的核心思想与应用
LeetCode_283_移动零
1. 题目描述与初步解题思路

这道题的要求与难点在于,不能复制数组,作者这里索性理解成,不能开辟额外空间,其实,若允许开辟额外空间,那这道题都没有任何意义了:
- 开辟一个
vector<int> arr - 遍历nums,将其中非0值emplace_back进arr
- 将arr不足size的空间全部emplace_back(0)
- 然后swap就得到了正确答案
但问题就在于,禁止开辟新空间,那么破题点在哪里呢?首先,既然已经意识到,使用两个相同数组进行操作,这道题会相当简单,而双指针法,又可以理解成是将指向两个相同数组的单指针指向了同一个数组,那么,可以尝试使用双指针往上面使用新数组的方式去靠,首先,上面的方案中,起始位置均为下标为0的位置,那么:
2. 双指针解题思路
- 先让两个指针i1, i2均指向nums的0下标处,其中i1相当于新开辟的数组,i2相当于指向源数组
然后当i2指向的数据是非0值时,就swap(nums[i1++], nums[i2++]),直至i2遇到0时,此时i1也指向0,这时就相当于遍历源数组时遇到了0,那接下来就需要继续移动i2,直到非0值,然后将该值swap(nums[i1++], nums[i2++]),接下来重复i2的移动即可- 执行2到i2指向nums最后一个元素时,题目就完成了
3. 基础代码实现
初步代码为:
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
//首先定义两个指针
int i1 = 0, i2 = 0;
//使用双指针算法
for (int i2 = 0; i2 < nums.size();)
{
//将i1移动至左侧第一个0的位置
while (i1 < nums.size() && nums[i1])//注意循环导致的越界问题
{
++i1;
}
//将i2移动至i1后的第一个非0值的位置
while (i2 < nums.size() && (!nums[i2] || i2 < i1))
{
++i2;
}
//判定两指针是否有越界情况,若i1越界,就表示数组中没有0,若i2越界,就表示i1越界或i1后没有非0值,且第二种情况在双指针处理结束后一定会出现
if (i2 < nums.size() && i1 < nums.size())
{
swap(nums[i2], nums[i1]);
}
}
}
};4. 细节处理与代码优化
- 首先,上述代码中i1的while循环其实完全可以省略,原因是,上述代码本质是想简化流程"将2化简可以得到:先开始移动两个指针,然后i1遇到0时停下,i2在遇到i1后的第一个非0值时停下,然后swap(nums[i1++], nums[i2++]),接下来重复i2的移动即可",但事实上,在代码实现的角度,反而增加了代码量,大可以按照上述3不走,尝试写为代码会发现,简洁的多
- 由于上述代码中使用while来快速移动i1与i2,所以就需要多加注意越界访问的情况,而上述代码通过i2/1 < nums.size()很好的进行了处理
5. 优化后的代码
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
//首先定义两个指针
int i1 = 0, i2 = 0;
for(i2 = 0; i2 < nums.size(); ++i2)
{
//当i2指向的数据不为0时,交换i1与i2指向的数据(相当于从空vector开始进行emplace_back操作)
if(nums[i2])
{
swap(nums[i1++], nums[i2]);
}
}
}
};LeetCode_27_移除元素
1. 题目描述与初步解题思路

其实稍微读读题,就能发现27和上面的移动零一模一样,只是多了个计数器,那么,直接给出代码
2. 代码
cpp
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i1 = 0, i2 = 0;
int count = 0;
for(i2 = 0; i2 < nums.size(); ++i2)
{
if(nums[i2] != val)
{
swap(nums[i1++], nums[i2]);
++count;
}
}
return count;
}
};3. 代码优化
没错,尽管已经如此精简,但翻阅评论区发现,有一个点可以被优化!就是count可以不要,处理结束后i1天然为非val数的个数
4. 优化后的代码
cpp
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i1 = 0, i2 = 0;
for(i2 = 0; i2 < nums.size(); ++i2)
{
if(nums[i2] != val)
{
swap(nums[i1++], nums[i2]);
}
}
return i1;
}
};LeetCode_1089_复写零(难题)
1. 题目描述与初步解题思路
这道题的难点主要也在禁止创建新空间,不然直接:
- 创建新
vector<int> res - 遍历源数组arr,遇到非零值emplace_back(),遇到零,emplace_back(0)两次
- 每次emplace_back之前判断res.size()是否==arr.size()即可
但可惜的是,仍旧是不允许创建新空间,那么,根据上面的思路总结,就差不多该意识到可以尝试双指针算法了,那么,思路也就有了:
- 首先,由于题目要求复写0,所以若不对0后面的元素进行操作,一但进行复习操作,一定会有数据被覆盖掉,因此,
在复写之前,需要先对后续数据进行处理,那么,首先想到的办法就是,在每次确定需要复写时,将0后的所有元素向后移动一次(可以设置一个每次复写时都指向数组倒数第二个元素的指针,然后复写之前指针一边前移一边将指向的元素后移 - 设置一个指针用于遍历数组,初始状态先指向数组开头,然后遍历数组,遇到0进行复写即可
2. 代码
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int mov = arr.size() - 2;//需要指向数组的倒数第二个元素
int ptr = 0;
while(ptr < arr.size())
{
//当ptr指向的元素不为0时
if(arr[ptr])
{
++ptr;
}
//当ptr指向的元素为0时
else
{
//先移动ptr后的元素
while(mov > ptr)
{
arr[mov + 1] = arr[mov];
--mov;
}
//移动完数据后重置mov
mov = arr.size() - 2;
//开始进行复写操作
if(ptr != arr.size() - 1)//复写之前记得先判断下ptr是否已经指向了最后一个元素,避免复写时造成越界访问
{
arr[ptr + 1] = 0;
}
ptr += 2;//+2要写到判断是否为最后一个元素的if语句外,避免死循环
}
}
}
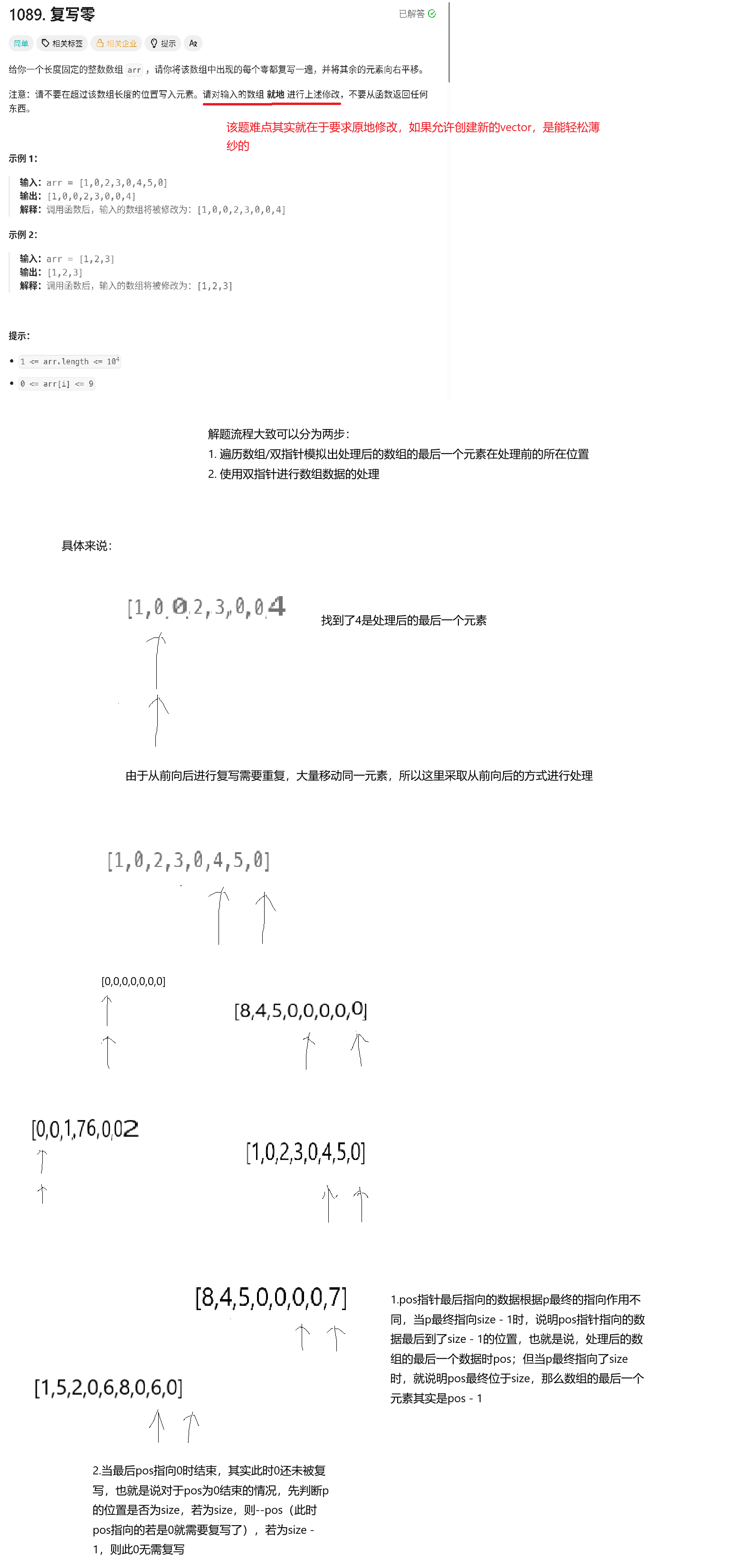
};3.思路优化(模拟定位 + 逆向复写法)
上面暴力解法的时间复杂度是O(n^2),但实际上,可以通过双指针写出时间复杂度仅为O(n)的思路,上面暴力解时间复杂度高的原因就在于对于同一个元素,需要多次重复移动,那么,有没有什么办法直接确定复写之后每个元素的位置呢?答案是先使用双指针模拟复写过程,找到复写后的数组的最后一个元素,然后直接将所有元素一次性移动到位,虽然提到了一次性移动到位,但真实践起来会发现,说起来简单,但要如何操作呢?很显然不能在从头开始遍历,遇到0时,把0后面所有数据都后移了(原因是这些数据中很可能也存在0),既然如此,就要想办法不移动0的数据,那么,自然而然就想到了ptr从后向前遍历数组这个思路,那么整体思路为:
- 先使用两指针i1,i2遍历一次源数组,以
模拟复写0方式找到正确处理后的最后一个元素,遍历结束后,i1指向处理后的最后一个元素,具体的模拟过程:i1,i2初始值为0,然后判断i1指向的数据是否为0,若非零,则++i1,++i2,若为0,则++i1,i2 += 2,当i2 == size/size - 1时,结束遍历,此时i1即为所求 - 再使用i3指针从i2开始由后向前遍历数组,同时,设置i4指针初始指向数组末尾,
遇到非零元素,依次移动到i4位置,然后--i4,遇到0,则先将0移动至i4,然后--i4也被填充为0(复写0),再--i4......当i3指向数组头部时,表明已经复写完毕了
4. 优化后的注意事项
尽管上面的思路看起来是比较好理解的,但实际操作时会出现很多细节问题:
- 在第一步的模拟操作中,循环条件需要确定,
为了确保循环停止时,i1指向处理后的数组的最后一个元素,需要将循环条件设置为i2 < size - 1(这样设置,意味着i2在最后一次进入循环移动之前的位置是处理前数组的倒数第二个元素或倒数第三个元素且该元素为0) - 紧接注意点1,循环结束后,i2最终值其实有两种情况,一是size,此情况表示在处理结束后的i1 - 1位置的元素是0,因此,i2在最后一次移动(移动前处于size - 2的位置)时,移动了两步;而二就是size - 1,该情况表示,i1 - 1的位置不是0或i1 - 2的位置为0,那么,为什么要重点注意这个细节呢?原因是,
如此进行模拟操作,那最终i1指向的数据最终会被写到i2的位置,因此,当i2以size结束时,i1其实并非处理后数组的最后一个数据,i1 - 1才是,所以,在模拟结束后,需判断i2的值,来确保i1是否需要-1才能指向真正的所求 - 仍旧是第一步模拟操作的问题,模拟后,可能出现i1指向的元素为0的情况(首先明确一点,若是上述i2 == size的情况,则已经进行了--i1的操作,这里指的最后一个元素就是真正的处理后的数组的最后一个元素),那么,这个0是否需要被复写呢,这里仍旧需要分情况讨论,事实上,
当目前指向的0是--i1后的结果,则该零其实就是造成上述2中i2 == size问题的罪魁祸首,那很显然,该0是需要进行复写的(正因为这个0的存在,才将本应位于数组最后一个位置的arr[i1]挤到了size的位置,因此,需要复写),而当此处的0是i2 == size - 1的情况,就不需要复写(循环结束后才指向该元素,说明未对该0进行复写时,i2已经到了size - 1,既然模拟时没有复写,那实际处理时自然无需复写)
5. 优化后的代码
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
//模拟确定处理后最后一个元素的位置
int i1 = 0, i2 = 0;
while(i2 < arr.size() - 1)
{
//当i1指向的元素非零时
if(arr[i1])
{
++i1;
++i2;
}
//当i1指向的元素为0时
else
{
++i1;
i2 += 2;
}
}
//进行i1的矫正
if(i2 == arr.size())
{
--i1;
}
//使用双指针正式进行复写操作
int i3 = i1, i4 = arr.size() - 1;
//判断一下i1指向的数据是否为0,进行分类处理
if(arr[i1] == 0 && i2 == arr.size() - 1)
{
arr[arr.size() - 1] = 0;
--i3;
--i4;
}
while(i3 >= 0)
{
//当i3指向的数据不为0时
if(arr[i3])
{
arr[i4--] = arr[i3];
}
//当i3指向的数据为0时
else
{
arr[i4--] = 0;
arr[i4--] = 0;
}
--i3;
}
}
};注:上述代码更注重复刻上述思路,其实有些地方可以简化,但就不能一一对应上述思路了,所以未采取
LeetCode_1_两数之和
1. 题目描述与初步解题思路
这道题目真的是经典中的经典了,是所有人正式刷LeetCode的第一题:

作者第一次做是只写出来的暴力解,真的想不到其他简洁方式了,然后还看到了评论区的这句话

顿时就绷不住了,好了,回忆结束,正式开始攻克这LeetCode的第一道坎
首先,最容易想到的办法自然是暴力解,即遍历所有可能,然后返回下标,但时间复杂度太高,也很简单,这里就不提了,重点来说说时间复杂度为快排O(n*logn) + 双指针法O(n) + 哈希映射快速查找源数组数据下标O(1)-》O(n*logn)的思路:
-
首先,不少题目使用双指针法的前提其实是数组有序(当然,这不是硬性要求,毕竟上面的题目都没有这个要求),这道题就是这样,想要完美利用双指针就要先确保这点
-
正式来说说思路,其实就一个核心方法,
设置两个指针front与back分别指向升序数组的首尾,然后将当前两指针指向的数据的和相加,若该和大于target,则向左移动back(--back),若该和小于target,则向右移动front(++front)核心思路的解释:作者其实好奇过通过上述方式真的不会错过一些合理的数吗,比如说,当两指针指向的数据的和大于target时,为什么不尝试--front呢(首先要明确,能够--front,说明至少
front指针目前绝对不指向数组开头,这也是下面思考的前提),但仔细思考过后就能发现,`当前两指针的指向可能由两种情况得来:-
一是上一步发生了--back,即4 + 比当前back更大的值,结果仍大,那也就说明,当前的front - 1是在与比back更大的数相加时,由于和小,才进行了++front,而由于是有序数组,且back目前指向了更小的值,显然向前移动多少次,和都一定是小值 -
二是上一步发生了++front,此情况说明,当前的front - 1指向的数据与当前back指向的数据的和较小,二由于有序数组,所以显然此情况无论怎样向前移动front,和都会是小值
因此可以证得,
--front来减少和的方式绝不可能得到正确答案,反之同理,当和小的时候也不能通过++back来得到正确结果,上述思考只是想证明该核心算法的正确与严谨性,实际上,上面的过程就算真的成立,也无法达到逐渐缩小数组查找区间的效果,不过上述思考还可以得出一个大些的结论,双指针法的一个不变性:在每一步中,front左边的元素和 back右边的元素都已经被证明不可能与对方区域的任何元素组成解

-
-
对于本题,还有一点需要注意,就是,sort过后得到的数组与源数组下标不同,而题目要求返回源数组数据的下标,关于这点,大致有三种解决办法
- 在sort之前,先使用hash记录源数组中数据与下标之间的对应关系
- 创建一个新数组
vector<int> index,用于记录源数组每个数据的索引,然后对该数组使用nums[a] < nums[b]仿函数进行与源数组数据的相同排序,这样排序后的源数组与index数组之间的下标就是连通的 - 也可以直接创建一个
vector<pair<int, int>> arr,直接使用仿函数进行快排,然后对该数组使用双指针即可
综上,这里决定选取空间复杂度最低的法二
2. 代码
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
//将源数组的下标存储到index数组中
vector<int> index(nums.size());
for(int i = 0; i < nums.size(); ++i)
{
index[i] = i;
}
//对index数组与源数组进行快排(这里需要注意,要先快排index)
sort(index.begin(), index.end(), [&nums](int a, int b)->bool{return nums[a] < nums[b];});// 引用捕捉nums,以便sort函数内部可以使用nums
sort(nums.begin(), nums.end());
//核心思路,双指针法解决问题
int front = 0, back = nums.size() - 1;
while(front < back)
{
//和大--back
if(nums[front] + nums[back] > target)
{
--back;
}
//和小++front
else if(nums[front] + nums[back] < target)
{
++front;
}
//相等说明找到了,直接退出循环
else if(nums[front] + nums[back] == target)
{
break;
}
}
//使用index索引数组找到两指针指向的数据的源数组下标
return vector<int>({index[front], index[back]});
}
};3. hash解法
上面提到了"不少题目使用双指针法的前提其实是数组有序",其实就是,当数组有序时往往推荐尝试双指针,但若数组不有序,那仅仅sort就会产生O(n * logn)的时间复杂度,其实,对于无序数组,往往可以采取hash解法,像这道两数之和就是,采用hash解法的时间复杂度仅为O(n)
简单说一下思路,通过i遍历数组,将数组的数据作为key,下标作为value,emplace进hash,再emplace的同时通过hash.find(target - arr[i]) != hash.end()进行判断即可
代码
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> um;
int i = 0;
for(i = 0; i < nums.size(); ++i)
{
if(um.find(target - nums[i]) != um.end())
{
break;
}
um[nums[i]] = i;//注意这里的emplace操作要写到if语句后面,以避免出现nums[i]与自己相加==target的不符合题意的情况
}
return vector<int>({i, um[target - nums[i]]});
}
};细节:[]重载要写到if判断后,以避免同一元素的和==target
LeetCode_15_三数之和
1. 题目描述与初步解题思路

三数之和其实就是两数之和的升级版,需要额外判断一个数,但其实,可以通过一个很简单的数据思维,将其转换为两数之和,这个思维就是,先指定出第一个数num1,然后从其他数中找到target == -num1的数,这样题目就有转变为了两数之和,但需要注意,由于num1可以任选(就算优化,也必须是数组中所有非正数/非负数范围),所以查找时时间复杂度会比两数之和多一次O(n),即该题目使用上述思路的时间复杂度为O(n^2 + nlogn)
2. 细节与优化
- 同时,还有一个点需要注意,三数之和的题目中要求了禁止三元组重复,对于去重而言,第一个想到的当然就是hash,但是,为了锻炼思维,其实还可以:
由于数组有序,所以在上述双指针查找的过程中,每次移动指针i1/i2/i3都可以将指针移动至不同于当前值的位置来达到去重效果(注意,这里并非找到三数之和为0才可以使用while跳过重复值,只要移动指针就可以使用while进行跳过) - 由于数组已经有序,且在查找i1,i2,i3指向和和为0的情况,并且i1位于三指针最左,所以当i1指向的数据>0时,后续就不可能找到了,因此,
当nums[i1] > 0时,直接break即可
3. 代码
cpp
//呃,时隔几天的第三次,用时9min,主要是意识到了不仅仅在==情况下使用while优化,
//事实是,每次移动指针,都可以采取while来跳过重复值
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> vvi;
sort(nums.begin(), nums.end());
for (int i1 = 0; i1 < nums.size() - 2;)//条件为size - 2,为i2,i3留出空间,且由于循环中会调整i1,所以此处第三个语句为空即可
{
//优化1.当i1指向的数据为正数后,由于数组有序,所以后面一定无法找到三数和为0的数了,退出循环即可
if (nums[i1] > 0)
{
break;
}
int i2 = i1 + 1, i3 = nums.size() - 1;
while (i2 < i3)
{
if (nums[i2] + nums[i3] == -nums[i1])
{
vvi.emplace_back(vector<int>{nums[i1], nums[i2], nums[i3]});
//优化2.每次移动指针,都可以直接进行跳过重复值操作
while (i2 < i3 && nums[++i2] == nums[i2 - 1])
{
}
while (i2 < i3 && nums[--i3] == nums[i3 + 1])
{
}
}
else if (nums[i2] + nums[i3] < -nums[i1])
{
while (i2 < i3 && nums[++i2] == nums[i2 - 1])
{
}
}
else if (nums[i2] + nums[i3] > -nums[i1])
{
while (i2 < i3 && nums[--i3] == nums[i3 + 1])
{
}
}
}
//优化3.每次移动i1,都跳过重复值
while (i1 < nums.size() - 2 && nums[++i1] == nums[i1 - 1])
{
}
}
return vvi;
}
};LeetCode_18_四数之和(难题)
1. 题目描述与初步解题思路
本题就是三数之和plus,整体思路没什么可说的了,仍旧是先固定一个i1,然后在i1后面的数据中找三数之和

2. 细节与代码优化
本题目中数据范围为-10^9 <= nums[i] <= 10^9,这是一个很重要的信息,由于int类型接收的最大值为21亿左右,而本题四数之和,4个int相加会导致int计算时溢出,这里需要采取在表达式中使用强转的方式,迫使计算时发生整型提升,以正确进行计算- 需要注意,
size()函数的返回值类型为size_t类型,而由于代码中使用了size() - 3等表达式,会导致计算结果转为极大值,而对于此情况,简单的解决办法有两种,一是可以使用const int size直接接收size()函数的结果,后续需要size()时,直接使用size变量即可,好处是后续使用size()无需再调用函数了;二是可以在搜索之前,先判断size()是否小于4,若小于四,则根本不可能有四数之和,直接返回空的vvi即可,好处是,面对此类情况,可以直接省去后续流程,提高效率
3. 代码
cpp
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
//创建返回用对象
vector<vector<int>> vvi;
//第0步,若size < 4,则直接返回空即可-》该步间接避免了nums.size()函数返回值为size_t类型,导致0 - 1出现极大值的问题
if (nums.size() < 4)
{
return vvi;
}
//第一步,先将数组排序
sort(nums.begin(), nums.end());
//查找四数之和
for (int i = 0; i < nums.size() - 3;)//这里-3是为后面三个数腾出空间,避免四个数中有重复指向
{
//先创建一个变量用于存放第一个数
int num1 = nums[i];
//查找三数之和
for (int j = i + 1; j < nums.size() - 2;)//j的起始值为i + 1,且三数之和时条件为-2,为left与right腾出空间,避免重复指向
{
//创建三数之和的第一个数
int num2 = nums[j];
//创建两指针
int left = j + 1;
int right = nums.size() - 1;
//双指针法进行处理
while (left < right)
{
long long int mid = static_cast<long long int>(nums[left]) + static_cast<long long int>(nums[right]) + static_cast<long long int>(num2);//由于LeetCode给的每个数值的范围为10^9,所以不能三连加,这里就需要强转,否则会发生整形溢出
//当大于时
if (mid > target - num1)
{
--right;
}
//当小于时
else if (mid < target - num1)
{
++left;
}
//当等于时
else if (mid == target - num1)
{
vvi.emplace_back(vector<int>({ num1, num2, nums[left], nums[right] }));
//使left与right跳过重复数
while (left < right && nums[++left] == nums[left - 1])//注意越界访问的问题,要使用条件加以限制
{
}
while (right > left && nums[--right] == nums[right + 1])
{
}
}
//处理未预料到的情况
else
{
assert(false);
}
}
//处理num2,跳过重复数值
while (j < nums.size() - 2 && nums[++j] == nums[j - 1])
{
}
}
//处理num2,跳过重复数值
while (i < nums.size() - 3 && nums[++i] == nums[i - 1])
{
}
}
return vvi;
}LeetCode_611_有效三角形的个数
1. 题目描述与初步解题思路

这道题目也是典型的可以使用双指针来解决的问题,先来补充一点基础的数学知识,三角形的判定:课本中学的,往往是,任意两边大于第三边即为三角形,但这种说法需要判定三次,其实,只要保证最短的两条边之和大于最大的那条边,就可以构成三角形,毕竟,接下来拿最大这边加任意一个小边,都一定比另一个小边长,那么,来谈谈具体的解题思路吧:
- 首先,对于一个数组,并且两数之和相关的问题,就要开始大胆尝试双指针算法了,那么对于两数之和使用双指针,就要求数组是有序的,因此,
第一步,先将数组sort - 然后,使用的算法有了,接下来开始思考如何解决这个问题,有没有发现,似乎和上面的三数之和有些共性?这里,先设置一个变量max存储nums[nums.size() - 1]作为三角形的最长边,然后设置两指针front,back,分别指向0和size() - 2,这里是不是就有两数之和那味了?不过,这里要找的是所有和大于max的值,与两数之和的==还是不同的,接下来具体看看应当如何移动指针:当两指针指向的数据小于等于max时,就需要进行指针的移动了,那么,很显然,需要扩大数据,肯定是要++front的,同时也能观察到,
当i1与i2指向的数据和大于max时,back与front ~ back - 1的任意一个指向的数据相加,都是所求,都能构建三角形,那么,只要front与back指向的数据和大于max,直接进行计数即可,无需继续向后移动front指针了,然后,就需要开始向前移动back指针,重复进行上述操作,一轮结束后,将max置为nums[nums.size() - 2]......
2. 细节与代码优化
- 使用sort后会隐藏一个细节,即
数组中元素可能为0,而0虽然是数,但显然不能靠0作为一个三角形的某条边,不过,使用sort+双指针算法,由于max前的数据一定<=max,所以当front指向0时,一定不能构成三角形 - 由于题目没有要求不能改变nums数组,所以我曾尝试每次找到max对应的元素后,直接pop_back(),但实际上,尽管pop_back()底层通过size成员变量实现O(1)尾删,但消耗终究还是比每次更换下标访问要大,因此,
建议直接每次--下标来查找max - 可以添加if (nums.size() < 3) return 0; 进行检查,数组长度小于3直接返回,可避免不必要的开销
数组的size可能<3,但最外层循环中使用i > 1作为循环条件就已经确保只有size > 3才能进入大循环,因此隐藏了这个细节问题,当然,不放心也可以通过第三点的size < 3直接return 0进行返回,同时避免开销
3. 代码
cpp
class Solution {
public:
int triangleNumber(vector<int>& nums) {
// 数组长度小于3直接返回
if (nums.size() < 3) return 0;
//定义计数器
int count = 0;
//先进行数组排序(默认升序)
sort(nums.begin(), nums.end());
//开始进行双指针算法
for (int i = nums.size() - 1; i > 1; --i)//i > 1,确保max前面至少有两个元素
{
int max = nums[i];
int front = 0;
int back = i - 1;
while (front < back)
{
//当两边之和小于等于max时
if (nums[front] + nums[back] <= max)
{
++front;
}
//当三边可以构成三角形时
else if (nums[front] + nums[back] > max)
{
count += (back - front);
--back;
}
}
}
return count;
}
};LeetCode_11_盛水最多的容器
1. 题目描述与初步解题思路
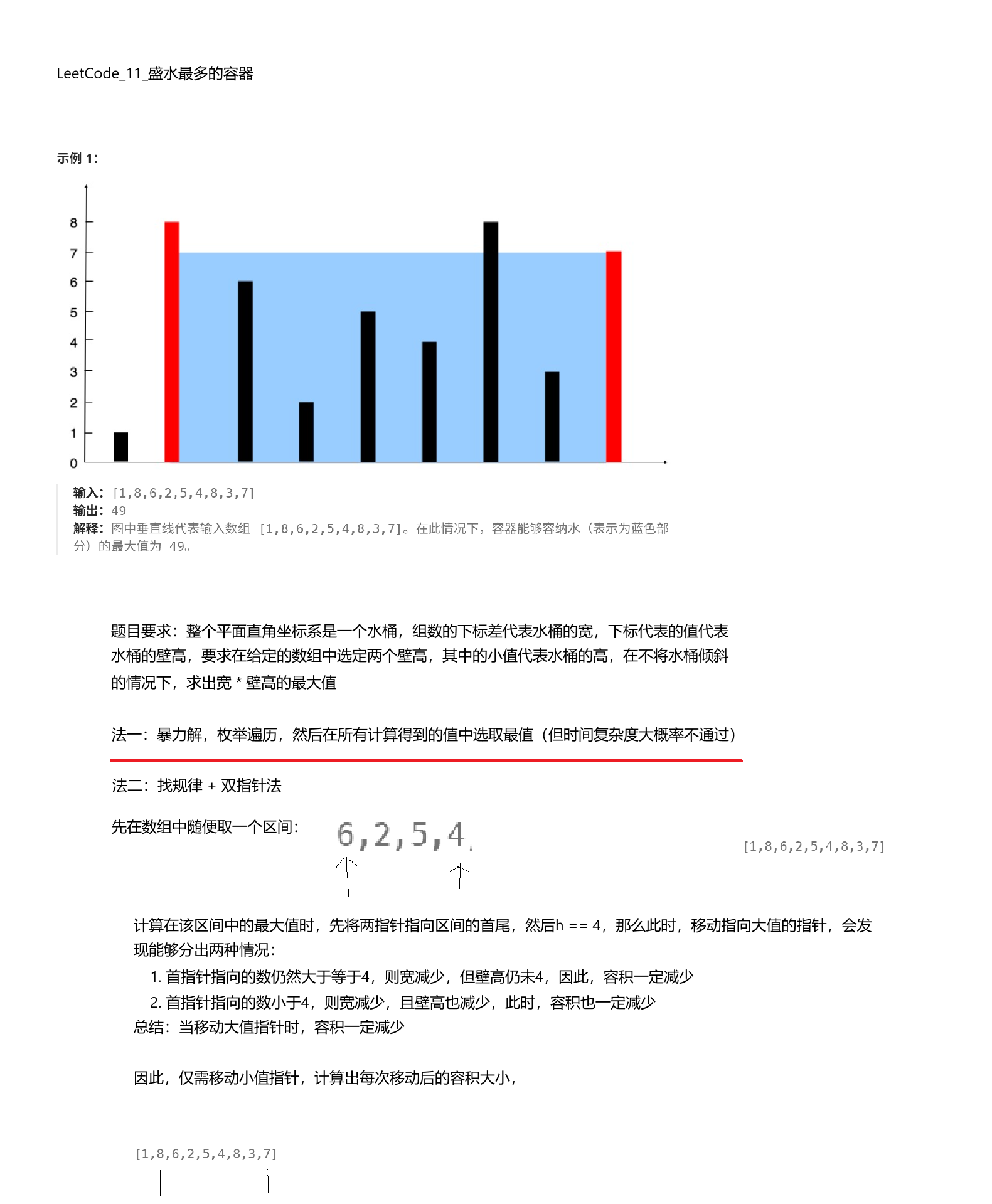
首先,第一步需要理解题目,这个平面直角坐标系的横坐标是一个木桶的底的长度,每个数组的值是构成木桶的两个木板的高,要找出两个木板,以其中的min作为木桶的高,两模板之间相差的下标值作为木桶底的长度,要求在不倾斜木桶的情况下找到最大容积,那么,首先可以分析出:这是有关一个数组,并查找其中两个元素的某种关系的题目,那么,这里就可以开始尝试双指针算法了,具体思路则需要找规律得到,这里先想象一下,当两指针分别指向区间的边界时,其实指向长木板那端的指针,无论如何移动,都不能找到比当前更大的容积了,具体原因可以分两种情况讨论:
- 当长木板的指针移动至更长或和自己高度一致的木板时,桶的高度仍然会是短的木板的高度,但由于是向区间内移动,所以桶的宽一定缩小了
- 当短木板的指针移动至更短的木板时,桶的高度会变为更短的木板的高度,且由于是向区间内移动,所以桶的宽也缩小了
至此,可以得出,当确定了一个容积后,想找到更大的容积,应该移动指向短木板的指针,那么解题思路也就出来了:
设置两个指针front与back,分别指向数组的左右边界,并计算出当前的容积每次移动短木板指针,并与目前得到的最大容积对比,若大,则更新用于存储最大容积的max变量,直至front >= back
2. 细节与代码优化
- 上述推理出了,要移动短木板的指针,那么,当两木板高度一致时,应该如何移动呢?答案是,移动哪边都可以,但绝不能不移动,原因是,上面提到的移动短木板指针是为了确保此次移动有找到更大容积的可能,但移动后,该指针可能会指向更长的数据,此时,移动另一个指针就可能会找到更大的容积,也就是说,当遇到遇到两木板高度一致时,此时的移动不是为了在这步找到更大的容积,而是为了后续移动,找到更大容积做铺垫
- 本题限制了size的范围至少为2,不过就算不限制,只要将max初始化为0,那么不进入循环,直接返回0也能正确解决该问题
3. 代码
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
size_t front = 0;
size_t back = height.size() - 1;
int max = 0;//记录遍历过程中计算出的容积最大值
while (front != back)
{
int bucketHeight = height[front] >= height[back] ? height[back] : height[front];
//更新max值
if (max < (back - front) * bucketHeight)
{
max = (back - front) * bucketHeight;
}
//开始双指针法
if (height[front] >= height[back])
{
--back;
}
else
{
++front;
}
}
return max;
}
};LeetCode_202_快乐数
1. 题目描述与初步解题思路

首先,这道题的第一个难点在于理解题目中的无限循环,其实,这个无限循环指的是一个数经过上述计算过程,到最后如果不到1,也一定会变成之前出现过的某个数字,如果不说明这点,该题难度就会大大上升,但其实证明思路很简单:
- 使用鸽巢原理:n个鸽巢中有n + 1只鸽子,那么一定至少存在一个鸽巢里存在n + 1 - n + 1 == 2只鸽子的情况
- 首先,题目说明了,数字的范围在2 ^ 31 - 1(21亿左右)以内,那么这里干脆取一个各位数字平方和最大的十位数:9999999999(99亿多),用以找到十位数中各位数字最大平方和的值,结果自然是9 ^ 9 * 10 = 810,也就是说,在题目范围内的数字,无论循环计算多少次,结果一定是0 ~ 810以内的正整数,就算到了最差情况,到第811次循环时,也一定会出现和之前一样的数据(鸽巢原理)
那么,现在就可以将问题抽象为:一个正整数,循环上述操作,到最后一定会形成一个类似带环链表的形状(即出现重复数据),若出现了重复数据,就判断该数据是否为1(因为1各位数的平方和==1),若为1,则为快乐数,若不为1,则非快乐数,
值得一提的是,不会出现"在出现1之前出现了重复数据,但后续该数据能够为1的情况",那么,解法也就出来了,最先想到的肯定是哈希,然后,其实可以想到解决环状链表问题时的快慢双指针法,这里先来介绍双指针法:采取解决环状链表的思路,使用快慢指针,当两指针相遇时,一定在环内,然后判断该位置的数据是否为1,若为1,则为快乐数,若不为1,则非快乐数
上述提到的快乐数环状结构图例:
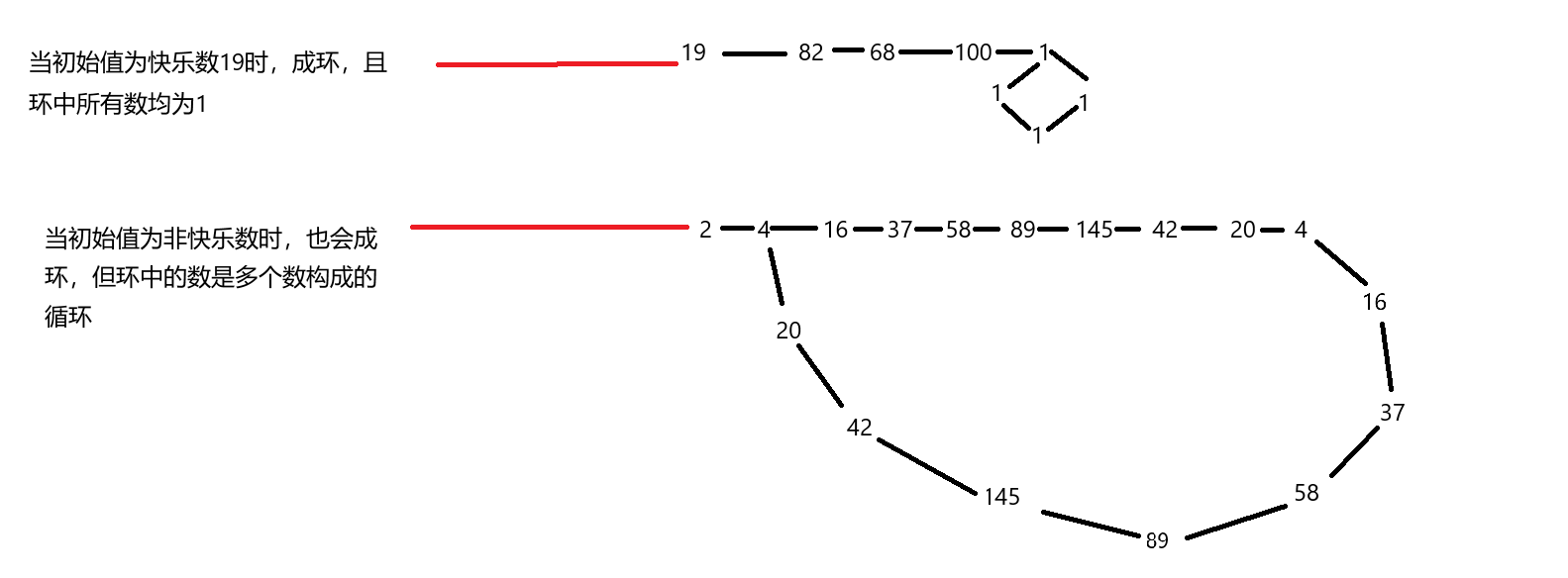
2. 细节与代码优化
- 可以将两模拟指针均初始化为n,然后使用do_while循环
- isHappy函数的返回值直接设置为return slow == 1;即可
- 回顾一下判断环状链表的一个结论:
无论两指针的速度差是多少,只要保证均为整数且存在环,则两指针必定在环内相遇
3. 代码
cpp
class Solution {
public:
bool isHappy(int n) {
int slow = n, fast = n;// 快慢指针初始化
do
{
slow = func(slow);
fast = func(func(fast));
}while(slow != fast);
return slow == 1;
}
int func(int num)// 快慢指针的计算函数
{
int final = 0;
while(num)
{
final += pow(num % 10, 2);
num /= 10;
}
return final;
}
};4. hash速解
cpp
class Solution {
public:
bool isHappy(int n) {
unordered_set<int> us;
while(us.find(n) == us.end())// 若发现相同数据,则表示已经入环,退出循环即可
{
us.emplace(n);//这里注意逻辑问题,要先写emplace再写func
n = func(n);
}
for(const auto& e : us)
{
cout << e << " ";
}
return n == 1;
}
int func(int num)// 快慢指针的计算函数
{
int final = 0;
while(num)
{
final += pow(num % 10, 2);
num /= 10;
}
return final;
}
};双指针算法总结
双指针大致可分为两种,一种是同向双指针,另一种是相向双指针,它们各有用途:
- 同向双指针一般会采取
快慢指针的方式进行数据去重(如删除重复元素),记录有效位置(如复写零)等题目 相向双指针一般会利用数组有序性,通过某种规律将指针移动,以求得所需(上述多数之和,三角形等),使用时往往能够将时间复杂度从O(n^2)降为O(n)/O(nlogn)(需要sort进行排序)- 当然,双指针的应用远不止以上两种,像是链表操作,字符串操作,数组操作等等体型都可能用到,但算法思想是类似的,这里就先不做展开,未来遇到更复杂的双指针题目会再进行补充
先写emplace再写func
n = func(n);
}
for(const auto& e : us)
{
cout << e << " ";
}
return n == 1;
}
int func(int num)// 快慢指针的计算函数
{
int final = 0;
while(num)
{
final += pow(num % 10, 2);
num /= 10;
}
return final;
}};
## 双指针算法总结
双指针大致可分为两种,一种是`同向双指针`,另一种是`相向双指针`,它们各有用途:
1. 同向双指针一般会采取`快慢指针`的方式进行数据去重(如删除重复元素),记录有效位置(如复写零)等题目
2. `相向双指针一般会利用数组有序性,通过某种规律将指针移动`,以求得所需(上述多数之和,三角形等),使用时往往能够将时间复杂度从`O(n^2)降为O(n)/O(nlogn)(需要sort进行排序)`
3. 当然,双指针的应用远不止以上两种,像是链表操作,字符串操作,数组操作等等体型都可能用到,但算法思想是类似的,这里就先不做展开,未来遇到更复杂的双指针题目会再进行补充