1.什么是路径类dp
路径类 dp 是线性 dp 的⼀种,它是在⼀个 n × m 的矩阵中设置⼀个⾏⾛规则,研究从起点⾛到终点的 ⽅案数、最⼩路径和或者最⼤路径和等等的问题。
⼊⻔阶段的《数字三⻆形》其实就是路径类 dp。
1.1.1 矩阵的最⼩路径和
题⽬来源: ⽜客⽹
题⽬链接: DP11 矩阵的最⼩路径和
难度系数: ★
描述
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
数据范围: 1 \le n,m\le 5001≤n,m≤500,矩阵中任意值都满足 0 \le a_{i,j} \le 1000≤ai,j≤100
要求:时间复杂度 O(nm)O(nm)
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:
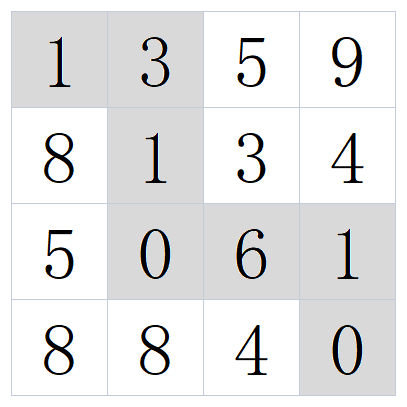
输入描述:
第一行输入两个正整数 n 和 m 表示矩阵 a 的长宽
后续输入 n 行每行有 m 个数表示矩阵的每个元素
输出描述:
输出从左上角到右下角的最小路径和
示例1
输入:
4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0复制输出:
12复制
示例2
输入:
2 3
1 2 3
1 2 3复制输出:
7【解法】
1. 状态表⽰:
dp[i][j] 表⽰:到达 [i, j] 位置处,最⼩路径和是多少。
那我们的最终结果就是 dp[n][m] 。
2. 状态转移:
到达 [i, j] 位置之前的⼀⼩步,有两种情况:
i. 从 [i− 1, j] 向下⾛⼀步,转移到 [i, j] 位置;
ii. 从 [i, j− 1] 向右⾛⼀步,转移到 [i, j] 位置。
由于到 [i, j] 位置两种情况,并且我们要找的是最⼩路径,因此只需要这两种情况下的最⼩值,再
加上 [i, j] 位置上本⾝的值即可: dp[i][j] = min(dp[i− 1][j], dp[i][j− 1]) + a[i][j] 。
3. 初始化:
第⼀⾏和第⼀列是要初始化的,因为会越界访问。
但是如果把整张表初始化为⽆穷⼤,然后把 dp[0][1] 和 dp[1][0] 的值设为 0 ,后续填表就是正确
的。
4. 填表顺序:根据「状态转移⽅程」的推导来看,填表的顺序就是「从上往下」填每⼀⾏,每⼀⾏「从左往
后」。
【参考代码】
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, m;
int f[N][N];
int main()
{
cin >> n >> m;
// 初始化
memset(f, 0x3f, sizeof f);
f[0][1] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
int x; cin >> x;
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + x;
}
}
cout << f[n][m] << endl;
return 0;
}1.1.2 「⽊」迷雾森林
题⽬来源: ⽜客⽹
题⽬链接: 「⽊」迷雾森林
难度系数: ★
链接:https://ac.nowcoder.com/acm/problem/53675
来源:牛客网
题目描述
赛时提示:保证出发点和终点都是空地
帕秋莉掌握了一种木属性魔法
这种魔法可以生成一片森林(类似于迷阵),但一次实验时,帕秋莉不小心将自己困入了森林
帕秋莉处于地图的左下角,出口在地图右上角,她只能够向上或者向右行走
现在给你森林的地图,保证可以到达出口,请问有多少种不同的方案
答案对2333取模
输入描述:
第一行两个整数m , n表示森林是m行n列
接下来m行,每行n个数,描述了地图
0 - 空地
1 - 树(无法通过)输出描述:
一个整数表示答案示例1
输入
复制3 3 0 1 0 0 0 0 0 0 0
3 3
0 1 0
0 0 0
0 0 0输出
复制3
3备注:
对于30%的数据,n,m≤100
对于100%的数据,n,m≤3,000
数据规模较大,请使用较快的输入方式,以下为快速读入模板
template<class T>inline void read(T &res)
{
char c;T flag=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}
scanf("%d",&x) -> read(x)
cin>>x -> read(x)
(调用方式:read(要读入的数))【解法】
1. 状态表⽰:
f [ i ][ j ] 表⽰:到达 [ i , j ] 位置时,有多少种⽅案。
那么 f [1][ m ] 就是我们要的结果。
2. 状态转移⽅程:
a. 如果 [ i , j ] 位置是空地,到达 [ i , j ] 位置有两种⽅式:
▪ 从 [ i + 1, j ] 向上⾛⼀步,此时的⽅案数为 f [ i + 1][ j ] ;
▪ 从 [ i , j − 1] 向右⾛⼀步,此时的⽅案数为 f [ i ][ j − 1] 。
两者总和就是到达 [ i , j ] 位置的总⽅案数。
b. 如果 [ i , j ] 位置是树,⽆法⾛到, f [ i ][ j ] = 0 。
3. 初始化:
可以在原始矩阵的规模上多加上⼀⾏和⼀列,把 f [ n + 1][1]或者f [ n ][0] 初始化为1 ,这样后
续填表就会有意义。
4. 填表顺序:
从下往上每⼀⾏,每⼀⾏从左往右。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 3010, MOD = 2333;
int n, m;
int a[N][N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
// 初始化
f[n][0] = 1;
for(int i = n; i >= 1; i--)
for(int j = 1; j <= m; j++)
if(a[i][j] == 0)
f[i][j] = (f[i][j - 1] + f[i + 1][j]) % MOD;
cout << f[1][m] << endl;
return 0;
}1.1.3 过河卒
题⽬来源: 洛⾕
题⽬链接: P1002 [NOIP2002 普及组] 过河卒
难度系数: ★
题目描述
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为"马拦过河卒"。
棋盘用坐标表示,A 点 (0,0)、B 点 (n,m),同样马的位置坐标是需要给出的。
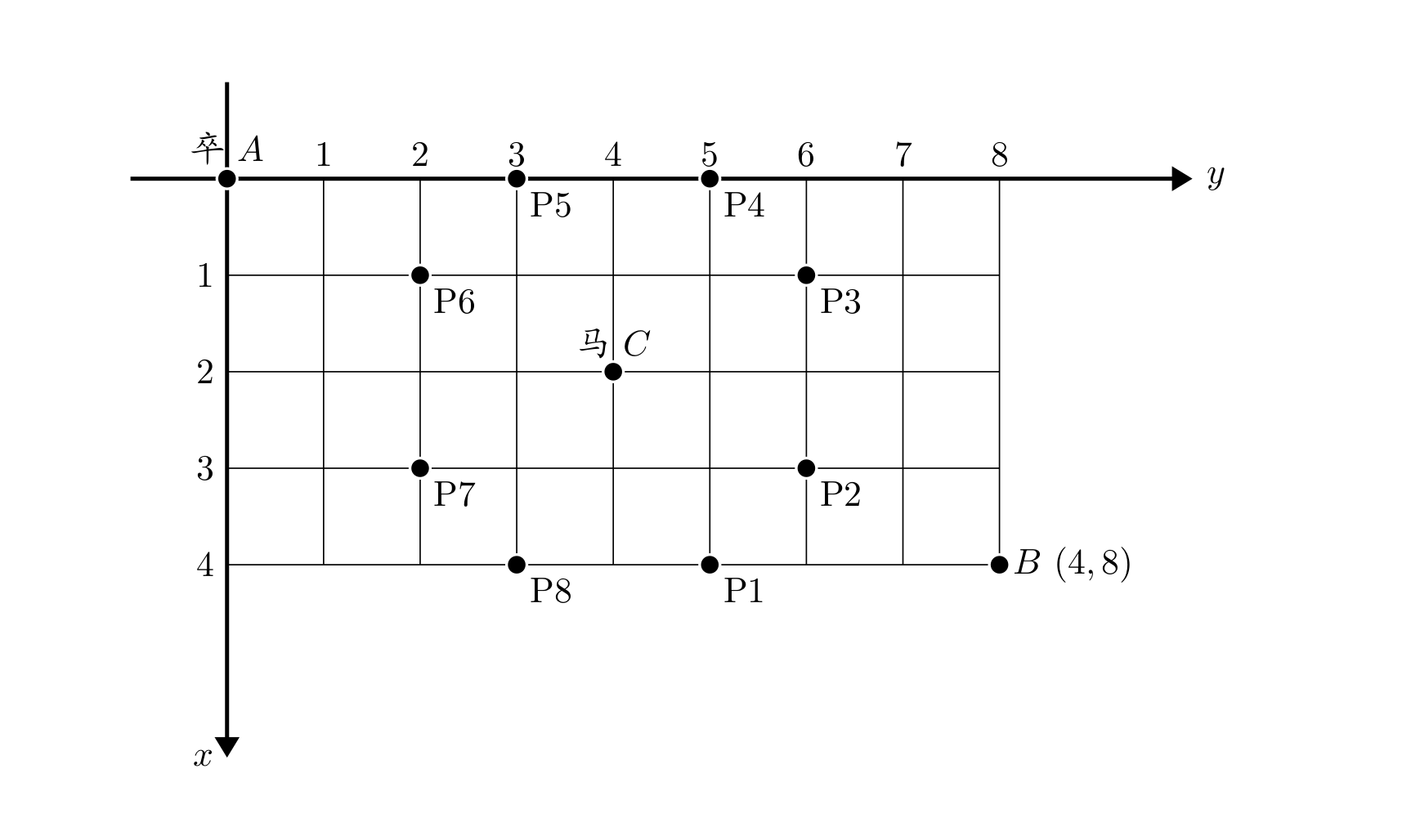
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例
输入 #1复制
6 6 3 3输出 #1复制
6说明/提示
对于 100% 的数据,1≤n,m≤20,0≤ 马的坐标 ≤20。
【题目来源】
NOIP 2002 普及组第四题
【解法】
1. 状态表⽰:
f [ i ][ j ] 表⽰:到达 [ i , j ] 位置的⽅案数。
那么 f [ n ][ m ] 就是我们要的结果。
2. 状态转移⽅程:
a. 如果 [ i , j ] 位置能⾛到,到达 [ i , j ] 位置之前的⼀⼩步,有两种情况:
▪ 从 [ i − 1, j ] 向下⾛⼀步,⾛到 [ i , j ] ,此时的⽅案数为 f [ i − 1][ j ] ;
▪ 从 [ i , j − 1] 向右⾛⼀步,⾛到 [ i , j ] ,此时的⽅案数为 f [ i ][ j − 1] ;
那么总⽅案数 f [ i ][ j ] = f [ i − 1][ j ] + f [ i ][ j − 1] 。
b. 如果 [ i , j ] 位置⾛不到, f [ i ][ j ] = 0 。
3. 初始化:
我们可以给原始的矩阵多加⼀⾏多加⼀列, n , m , x , y 全部 +1 ,这样填任何⼀个位置都不会越
界。 然后初始化 f [1][0] = 1 或者 f [0][1] = 1 ,保证后续填表正确即可。
4. 填表顺序:
从上往下每⼀⾏,每⼀⾏从左往右。
【参考代码】
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 25;
int n, m, a, b;
LL f[N][N];
// 判断是否是被⻢所拦截的点
bool check(int i, int j)
{
return (i == a && j == b) || (i != a && j != b && abs(i - a) + abs(j - b)
== 3);
}
int main()
{
cin >> n >> m >> a >> b;
n++; m++; a++; b++;
// 初始化
f[0][1] = 1;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
if(check(i, j)) continue;
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
cout << f[n][m] << endl;
return 0;
}1.1.4 ⽅格取数
题⽬来源: 洛⾕
题⽬链接: P1004 [NOIP2000 提⾼组] ⽅格取数
难度系数: ★★★
题目背景
NOIP 2000 提高组 T4
题目描述
设有 N×N 的方格图 (N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。如下图所示(见样例):
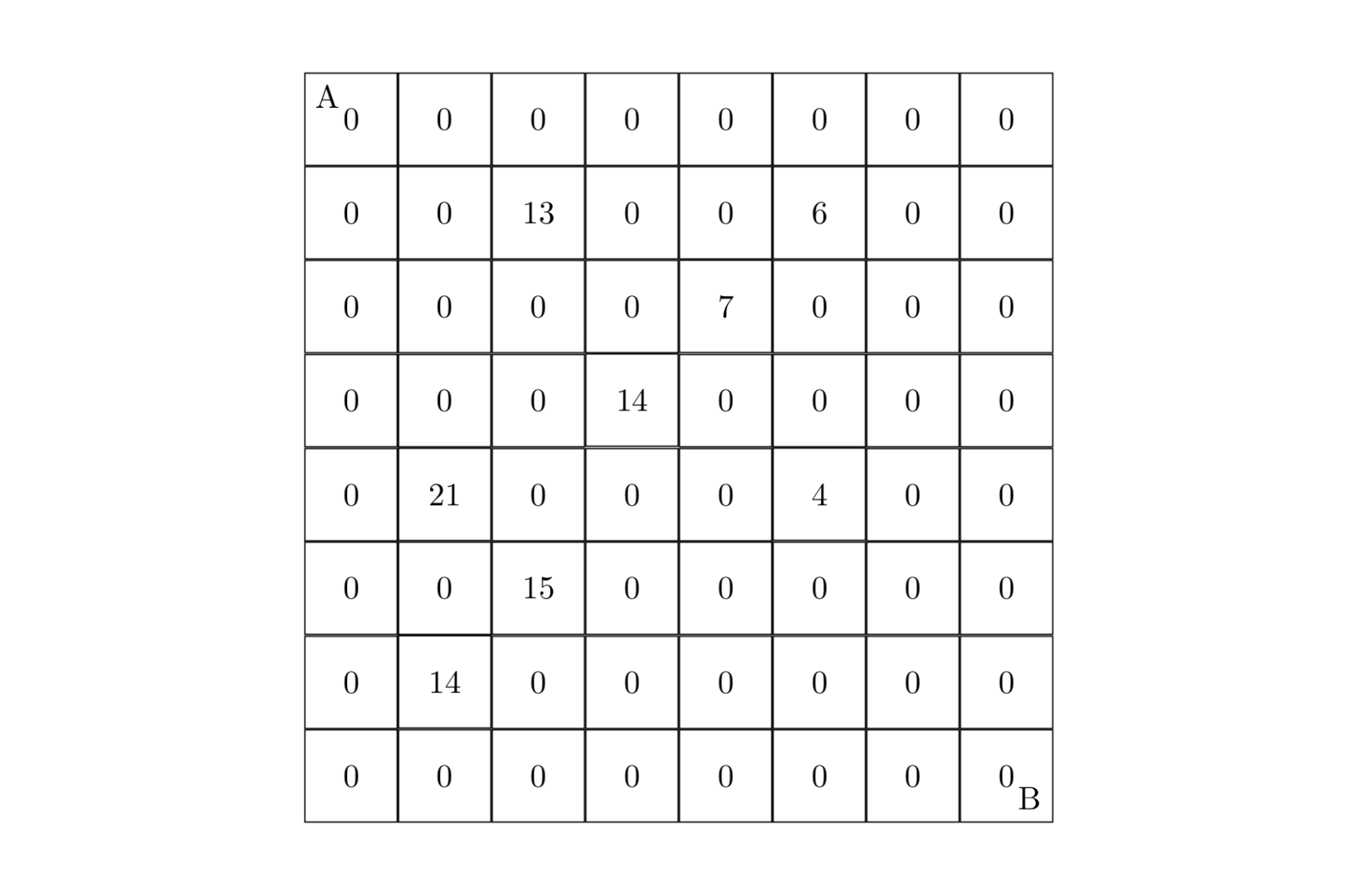
某人从图的左上角的 A 点出发,可以向下行走,也可以向右走,直到到达右下角的 B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 0)。
此人从 A 点到 B 点共走两次,试找出 2 条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 N(表示 N×N 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 0 表示输入结束。
输出格式
只需输出一个整数,表示 2 条路径上取得的最大的和。
输入输出样例
输入 #1复制
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0输出 #1复制
67说明/提示
数据范围:1≤N≤9。
【解法】
贪⼼ + 两次dp 是错误的,因为两次最优不等于全局最优,可以举出反例。正解应该是同时去⾛两条 路,两者相互影响,所以放在⼀起考虑。
1. 状态表⽰:
需要知道当前这两条路径⾛到什么位置,因此需要四维 f [ i 1 ][ j 1 ][ i 2 ][ j 2 ]来表⽰第⼀条路⾛到[ i 1 , j 1 ] 第⼆条路⾛到 [ i 2 ][ j 2 ]。
但是我们发现,因为两者是同时出发的,所以 横纵坐标之和是⼀个定值 。也就是说,只要知道了横
纵坐标之和,以及两者的横坐标,就可以计算出纵坐标,状态表⽰就可以优化掉⼀维。
优化后的状态表⽰:f [st][i1 ][i2 ]表⽰:第⼀条路在[i1 , st− i1 ] ,第⼆条路在[i2 , st− i2 ] 时,
两者的路径最⼤和。那我们的最终结果就是f[n× 2][n][n] 。
2. 状态转移⽅程:
第⼀条路可以从上[ i 1 − 1, st − i 1 ] 或者左[ i 1 , st − i 1 − 1] ⾛到 [ i 1 , st − i 1 ]位置;第⼆条路可 以从上 [ i 2 − 1, st − i 2 ] 或者左[ i 2 , st − i 2 − 1] ⾛到[ i 2 , st − i 2 ] 位置。排列组合⼀下⼀共4
中情况,分别是:
◦ 上 + 上,此时的最⼤和为: f [st − 1][i 1 − 1][i2 − 1] ;
◦ 上 + 左,此时的最⼤和为: f [st − 1][i 1 − 1][i2 ] ;
◦ 左 + 上,此时的最⼤和为: f [st − 1][i 1 ][i2 − 1] ;
◦ 左 + 左,此时的最⼤和为: f [st − 1][i 1 ][i2 ] ;
取上⾯四种情况的最⼤值,然后再加上a [ i 1 ][ j 1 ] 和 a [ i 2 ][ j 2 ]。但是要注意,如果两个路径当前在
同⼀位置时,只⽤加上⼀个a [ i 1 ][ j 1 ] 即可。
3. 初始化:
算的是路径和, 0 不会影响最终结果,直接填表。
4. 填表顺序:
先从⼩到⼤循环横纵坐标之和,然后依次从⼩到⼤循环两者的横坐标。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 15;
int n;
int a[N][N];
int f[N * 2][N][N];
int main()
{
cin >> n;
int x, y, w;
while(cin >> x >> y >> w, x)
{
a[x][y] = w;
}
for(int s = 2; s <= n + n; s++)
{
for(int i1 = 1; i1 <= n; i1++)
{
for(int i2 = 1; i2 <= n; i2++)
{
int j1 = s - i1, j2 = s - i2;
if(j1 <= 0 || j1 > n || j2 <= 0 || j2 > n) continue;
int t = f[s - 1][i1][i2];
t = max(t, f[s - 1][i1][i2 - 1]);
t = max(t, f[s - 1][i1 - 1][i2]);
t = max(t, f[s - 1][i1 - 1][i2 - 1]);
if(i1 == i2)
{
f[s][i1][i2] = t + a[i1][j1];
}
else
{
f[s][i1][i2] = t + a[i1][j1] + a[i2][j2];
}
}
}
}
cout << f[n + n][n][n] << endl;
return 0;
}2 经典线性 dp
经典线性 dp 问题有两个: 最⻓上升⼦序列(简称:LIS)以及最⻓公共⼦序列 (简称:LCS),这两道 题⽬的很多⽅⾯都是可以作为经验,运⽤到别的题⽬中。⽐如:解题思路,定义状态表⽰的⽅式,推 到状态转移⽅程的技巧等等。
因此,这两道经典问题是⼀定需要掌握的。
2.1 最⻓上升⼦序列(⼀)
题⽬来源: 洛⾕
题⽬链接: B3637 最⻓上升⼦序列
难度系数: ★
题目描述
这是一个简单的动规板子题。
给出一个由 n(n≤5000) 个不超过 106 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。
最长上升子序列是指,从原序列中按顺序 取出一些数字排在一起,这些数字是逐渐增大的。
输入格式
第一行,一个整数 n,表示序列长度。
第二行有 n 个整数,表示这个序列。
输出格式
一个整数表示答案。
输入输出样例
输入 #1复制
6
1 2 4 1 3 4输出 #1复制
4说明/提示
分别取出 1、2、3、4 即可。
【解法】
1. 状态表⽰
dp [ i ] 表⽰:以 i 位置元素为结尾的「所有⼦序列」中,最⻓递增⼦序列的⻓度。
最终结果就是整张 dp 表⾥⾯的最⼤值。
2. 状态转移⽅程:
对于 dp [ i ] ,我们可以根据「⼦序列的构成⽅式」,进⾏分类讨论:
▪ ⼦序列⻓度为 1 :只能⾃⼰玩了,此时 dp [i] = 1 ;
▪ ⼦序列⻓度⼤于1 :a[i] 可以跟在前⾯某些数后⾯形成⼦序列。设前⾯的某⼀个数的下标
为j ,其中 1 ≤ j < i − 1。只要a [j ] < a [i] ,i 位置元素跟在 j元素后⾯就可以形成
递增序列,⻓度为dp [j] + 1 。
因此,我们仅需找到满⾜要求的最⼤的 dp [j] + 1 即可。
综上, dp [i ] = max (dp [j ] + 1, dp [i ]) ,其中 1 ≤ j < i && nums [j ] < nums [i] 。
3. 初始化:
不⽤单独初始化,每次填表的时候,先把这个位置的数改成 1 即可。
4. 填表顺序:
显⽽易⻅,填表顺序「从左往右」。
【参考代码】
cpp
#include<iostream>
using namespace std;
const int N = 5010;
int n;
int a[N];
int f[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int ret = 0;
for(int i = 1; i <= n; i++)
{
f[i] = 1; // ⻓度为 1 的⼦序列
for(int j = 1; j < i; j++)
{
if(a[j] < a[i])
{
f[i] = max(f[i], f[j] + 1);
}
}
ret = max(ret, f[i]);
}
cout << ret << endl;
return 0;
}2.2 最⻓上升⼦序列(⼆)
题⽬来源: ⽜客⽹
题⽬链接: 【模板】最⻓上升⼦序列
难度系数: ★★
链接:https://ac.nowcoder.com/acm/problem/226831
来源:牛客网
题号:NC226831
时间限制:C/C++/Rust/Pascal 1秒,其他语言2秒
空间限制:C/C++/Rust/Pascal 256 M,其他语言512 M
64bit IO Format: %lld
题目描述
给你一个长度为n的数组,求最长的严格上升子序列的长度。
输入描述:
第一行一个整数n,表示数组长度。
第二行n个整数,表示数组中的元素。
1 <= n <= 100000
输出描述:
输出一行,表示答案。示例1
输入
复制5 1 2 2 2 3
5
1 2 2 2 3输出
复制3
3说明
最长的上升子序列为[1,2,3],长度为3.【解法】
利⽤贪⼼ + ⼆分优化动态规划:
• 我们在考虑最⻓递增⼦序列的⻓度的时候,其实并不关⼼这个序列⻓什么样⼦,我们只是关⼼最后 ⼀个元素是谁。这样新来⼀个元素之后,我们就可以判断是否可以拼接到它的后⾯。
• 因此,我们可以创建⼀个数组,统计⻓度为 x 的递增⼦序列中,最后⼀个元素是谁。为了尽可能
的让这个序列更⻓,我们仅需统计⻓度为 x 的所有递增序列中最后⼀个元素的「最⼩值」。
• 统计的过程中发现,数组中的数呈现「递增」趋势,因此可以使⽤「⼆分」来查找插⼊位置。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int f[N], len; // 注意与上⼀个动态规划数组的含义是不⼀样的
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++)
{
// 处理边界情况
if(len == 0 || a[i] > f[len]) f[++len] = a[i];
else
{
// ⼆分插⼊位置
int l = 1, r = len;
while(l < r)
{
int mid = (l + r) / 2;
if(f[mid] >= a[i]) r = mid;
else l = mid + 1;
}
f[l] = a[i];
}
}
cout << len << endl;
return 0;
}2.3 合唱队形
题⽬来源: 洛⾕
题⽬链接: P1091 [NOIP2004 提⾼组] 合唱队形
难度系数: ★★
题目描述
n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 k 位同学从左到右依次编号为 1,2, ... ,k,他们的身高分别为 t1,t2, ... ,tk,则他们的身高满足 t1<⋯<ti>ti+1> ... >tk(1≤i≤k)。
你的任务是,已知所有 n 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入格式
共二行。
第一行是一个整数 n(2≤n≤100),表示同学的总数。
第二行有 n 个整数,用空格分隔,第 i 个整数 ti(130≤ti≤230)是第 i 位同学的身高(厘米)。
输出格式
一个整数,最少需要几位同学出列。
输入输出样例
输入 #1复制
8
186 186 150 200 160 130 197 220输出 #1复制
4说明/提示
对于 50% 的数据,保证有 n≤20。
对于全部的数据,保证有 n≤100。
【解法】
对于每⼀个位置 i ,计算:
• 从左往右看:以 i 为结尾的最⻓上升⼦序列 f [ i ] ;
• 从右往左看:以 i 为结尾的最⻓上升⼦序列 g [ i ] ;
最终结果就是所有 f [ i ] + g [ i ] − 1 ⾥⾯的最⼤值。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 110;
int n;
int a[N];
int f[N], g[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
// 从左往右
for(int i = 1; i <= n; i++)
{
f[i] = 1;
for(int j = 1; j < i; j++)
{
if(a[j] < a[i])
{
f[i] = max(f[i], f[j] + 1);
}
}
}
// 从右往左
for(int i = n; i >= 1; i--)
{
g[i] = 1;
for(int j = n; j > i; j--)
{
if(a[j] < a[i])
{
g[i] = max(g[i], g[j] + 1);
}
}
}
int ret = 0;
for(int i = 1; i <= n; i++)
{
ret = max(ret, f[i] + g[i] - 1);
}
cout << n - ret << endl;
return 0;
}2.4 ⽜可乐和最⻓公共⼦序列
题⽬来源: ⽜客⽹
题⽬链接: ⽜可乐和最⻓公共⼦序列
难度系数: ★★
链接:https://ac.nowcoder.com/acm/problem/235624
来源:牛客网
题号:NC235624
时间限制:C/C++/Rust/Pascal 1秒,其他语言2秒
空间限制:C/C++/Rust/Pascal 256 M,其他语言512 M
64bit IO Format: %lld
题目描述
牛可乐得到了两个字符串 sss 和 ttt ,牛可乐想请聪明的你帮他计算出来,两个字符串的最长公共子序列长度是多少。
最长公共子序列的定义是,子序列中的每个字符都能在两个原串中找到,而且每个字符的先后顺序和原串中的先后顺序一致。
输入描述:
输入包含多组数据,请读至文件末尾。
每行包含两个字符串 s,ts,ts,t,两个字符串用一个空格字符间隔,单个字符串长度不超过 500050005000。
数据保证所有数据的字符串 sss 长度之和与字符串 ttt 长度之和均不超过 500050005000。
输出描述:
对于每组数据,输出一个整数,代表最长公共子序列的长度。示例1
输入
复制abccde bcee
abccde bcee输出
复制3
3说明
最长公共子序列长度为 bcebcebce,长度为 333。【解法】
1. 状态表⽰ :
dp [ i ][ j ]表⽰:s 1 的 区间[1,i ] 以及s 2 的 区间[1, j ]内的所有的⼦序列中,最⻓公共⼦序列的
⻓度。
那么 dp [ n ][ m ] 就是我们要的结果。
2. 状态转移⽅程:
对于 dp [ i ][ j ] ,我们可以根据 s 1[ i ] 与 s 2[ j ] 的字符分情况讨论:
a. 两个字符相同 :那么最⻓公共⼦序列就在 的 以及 的
区间上找到⼀个最⻓的,然后再加上 即可。因此 ;
s 1[ i ] = s 2[ j ] s 1 [1, i − 1] s 2 [1, j − 1]
s 1[ i ] dp [ i ][ j ] = dp [ i − 1][ j − 1] + 1
b. 两个字符不同 :s1[i]!=s2[j]那么最⻓公共⼦序列⼀定不会同时以s1[i] 和s2[j] 结尾。那么
我们找最⻓公共⼦序列时,有下⾯三种策略:
▪ 去 s 1 的 [1, i − 1] 以及 s 2 的 [1, j ] 区间内找:此时最⼤⻓度为 dp [ i − 1][ j ] ;
▪ 去 s 1 的 [1, i ] 以及 s 2 的 [1, j − 1] 区间内找:此时最⼤⻓度为 dp [ i ][ j − 1] ;
▪ 去 s 1 的 [1, i − 1] 以及 s 2 的 [1, j − 1] 区间内找:此时最⼤⻓度为 dp [ i − 1][ j − 1] 。 我们要三者的最⼤值即可。但是我们仔细观察会发现,第三种包含在第⼀种和第⼆种情况⾥
⾯,但是我们求的是最⼤值,并不影响最终结果。因此只需求前两种情况下的最⼤值即可。
综上,状态转移⽅程为:
if ( s 1[ i ] = s 2[ j ]) dp [ i ][ j ] = dp [ i − 1][ j − 1] + 1 ;
if ( s 1[ i ] != s 2[ j ]) dp [ i ][ j ] = max ( dp [ i − 1][ j ], dp [ i ][ j − 1])
3. 初始化:
直接填表即可。
4. 填表顺序:
根据「状态转移⽅程」得:从上往下填写每⼀⾏,每⼀⾏从左往右。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 5010;
string s, t;
int f[N][N];
int main()
{
while(cin >> s >> t)
{
int n = s.size(), m = t.size();
// s = " " + s, t = " " + t;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(s[i - 1] == t[j - 1]) f[i][j] = f[i - 1][j - 1] + 1;
else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
}
}
cout << f[n][m] << endl;
}
return 0;
}2.3.5 编辑距离
题⽬来源: 洛⾕
题⽬链接: P2758 编辑距离
难度系数: ★★★
题目描述
设 A 和 B 是两个字符串。我们要用最少的字符操作次数,将字符串 A 转换为字符串 B。这里所说的字符操作共有三种:
- 删除一个字符;
- 插入一个字符;
- 将一个字符改为另一个字符。
A,B 均只包含小写字母。
输入格式
第一行为字符串 A;第二行为字符串 B;字符串 A,B 的长度均小于 2000。
输出格式
只有一个正整数,为最少字符操作次数。
输入输出样例
输入 #1复制
sfdqxbw
gfdgw输出 #1复制
4说明/提示
对于 100% 的数据,1≤∣A∣,∣B∣≤2000。
1. 状态表示
dp[i][j] 表示:字符串 A 中 [1,i] 区间与字符串 B 中 [1, j] 区间内的编辑距离。最终要求的结果为 dp[n][m](其中 n 是字符串 A 的长度,m 是字符串 B 的长度)。
2. 状态转移方程
对于 dp[i][j],根据 A [i] 与 B [j] 的字符是否相同分情况讨论:
情况 1:两个字符相同(A [i] = B [j])此时 dp[i][j] 等价于 A 的 [1,i−1] 区间与 B 的 [1,j−1] 区间的编辑距离,即:dp[i][j] = dp[i − 1][j − 1]
情况 2:两个字符不同(A [i] ≠ B [j])对字符串 A 可执行三种操作,取操作次数最少的一种:
删除 A [i]:此时 dp[i][j] 等价于 A 的 [1,i−1] 区间与 B 的 [1,j] 区间的编辑距离 + 1(删除操作),即:dp[i][j] = dp[i − 1][j] + 1
插入字符:在 A 的末尾插入一个与 B [j] 相同的字符,此时 dp[i][j] 等价于 A 的 [1,i] 区间与 B 的 [1,j−1] 区间的编辑距离 + 1(插入操作),即:
dp[i][j] = dp[i][j − 1] + 1
替换字符:将 A [i] 替换为 B [j],此时 dp[i][j] 等价于 A 的 [1,i−1] 区间与 B 的 [1,j−1] 区间的编辑距离 + 1(替换操作),即:dp[i][j] = dp[i − 1][j − 1] + 1
最终取三者最小值:dp[i][j] = min(dp[i − 1][j], dp[i][j − 1], dp[i − 1][j − 1]) + 1
3. 初始化
当 i=0 或 j=0 时(其中一个字符串为空),编辑距离为另一个字符串的长度(全部删除 / 插入操作):
第一行:dp[0][j] = j(1 ≤ j ≤ m),表示空字符串 A 与 B 的 [1,j] 区间的编辑距离为 j(插入 j 个字符)。
第一列:dp[i][0] = i(1 ≤ i ≤ n),表示 A 的 [1,i] 区间与空字符串 B 的编辑距离为 i(删除 i 个字符)。
4. 填表顺序
初始化完成后,从 dp[1][1] 开始:
按从上到下遍历每一行;
每一行内按从左到右遍历每一列;
依次计算每个 dp[i][j] 的值,直至填满整个 dp 表。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 2010;
string a, b;
int n, m;
int f[N][N];
int main()
{
cin >> a >> b;
n = a.size(); m = b.size();
a = " " + a; b = " " + b;
// 初始化
for(int i = 1; i <= n; i++) f[i][0] = i;
for(int j = 1; j <= m; j++) f[0][j] = j;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
if(a[i] == b[j]) f[i][j] = f[i - 1][j - 1];
else f[i][j] = min(min(f[i - 1][j], f[i - 1][j - 1]), f[i][j -
1]) + 1;
}
cout << f[n][m] << endl;
return 0;
}