【机器学习】python使用支持向量机解决兵王问题(基于libsvm库)

1、基础概念

1.1什么是兵王问题

兵王问题是国际象棋残局的分析问题，在如下图白方有一兵一王、黑方仅有一王的情况下，一名专业的棋手可以根据场上三个棋子的位置来判断最终该盘棋是合棋还是白方获胜。

基础规则：

国王：每次行动可以向任意反向移动1格；

兵：第一次向前可以走1或2格，此后每次只能向前走1格，不可后退；

兵的升变：兵走至对方底线后可以升变为除王外的任意棋子；

逼和：一方的王未被将军，但其移动到任何地方都会被对方杀死，此时达成和棋；

由上述规则可推出：

1、黑方若想和棋，需防止白方将兵走至底线，否则兵变为王后配合白王必然可将死黑王；

2、黑方可以利用逼和规则，主动制造逼和的情况以达成和棋。

1.2什么是支持向量机SVM

简单理解，SVM追求二分类问题的最优解。例如在二维平面上寻找一条最"中间"的线来将两类物品分隔开，知乎上jinzhao老师的图形象地描绘出了这一场景。

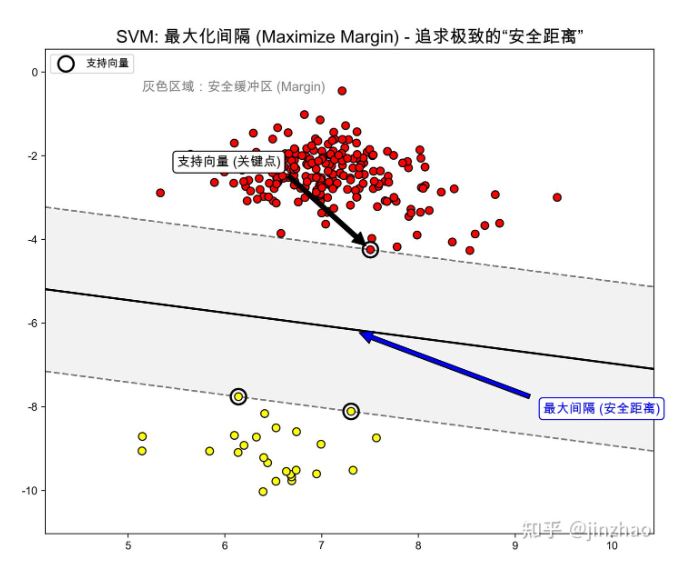
1.3支持向量机在兵王问题的应用

兵王问题中对于弱势方，此处设置为黑方来说，只有和棋或者输棋两种结果，这就是二分类问题。因此可以使用支持向量机利用已知棋局结果来训练出模型，从而预测新的棋局中黑方最终会和棋还是输棋。

2、获取数据集

UCI Machine Learning 中提供了兵王问题已标注好的数据集。

2.1理解数据集

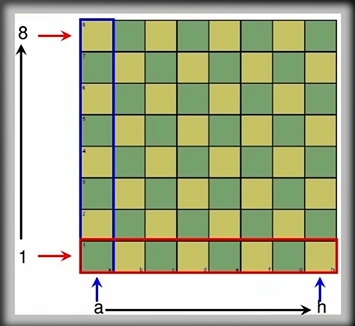
下图棋盘中a-h表示横坐标，1-8表示纵坐标。

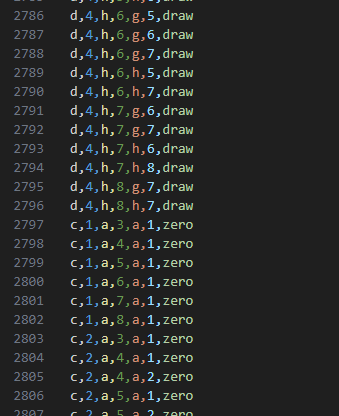
数据集中1、3列表示黑王位置，5、7列表示白王位置，9、11位置表示白兵位置，13列表示最终结果，draw为和棋，其余数字结果表示为白棋最多多少步后可获胜。

3、配置python环境

3.1基础环境

Anaconda环境。

3.2安装libsvm

使用以下指令：

pip install -U libsvm-official

该库的运行需要C环境支持，若电脑中此前未安装，命令行会给出相关的提示，根据指引通过Visual Studio Install安装MSVC环境即可。

4、编写代码

4.0训练所需头文件

from libsvm.svmutil import *
import os
import numpy as np

4.1提取数据集

读取文件并将数据存储，根据最终结果是否为"draw"分为正类和负类。

########################################################################
# 1、提取数据集：

# 获取当前 py 文件所在目录
current_dir = os.path.dirname(os.path.abspath(__file__))
# 拼接数据文件的绝对路径
file_path = os.path.join(current_dir, "krkopt.data")
# 打开数据文件,默认系统GB2312有乱码
with open(file_path, "r",encoding="utf-8-sig") as f:
    lines = f.readlines()

xapp = []  # 特征矩阵，每个样本是一个长度为6的向量
yapp = []  # 标签向量

for line in lines:
    line = line.strip()  # 去掉换行符
    if len(line) > 10:   # 过滤掉空行或不完整行
        parts = line.split(",")  # 按逗号分割
        # print(parts)

        # 提取特征：字母转数字 (a=1,b=2,...)，数字字符转数值
        vec = np.zeros(6, dtype=int)
        vec[0] = ord(parts[0]) - 96   # 第一个字母 a→1, b→2...
        vec[1] = int(parts[1])        # 第一个数字
        vec[2] = ord(parts[2]) - 96   # 第二个字母
        vec[3] = int(parts[3])        # 第二个数字
        vec[4] = ord(parts[4]) - 96   # 第三个字母
        vec[5] = int(parts[5])        # 第三个数字

        xapp.append(vec)
        # print(vec)
        # print(xapp)

    # 标签：如果第7个字符是 'draw' → 正类(+1)，否则负类(-1)
    if parts[6] == 'draw':
        yapp.append(1)
    else:
        yapp.append(-1)
#print(xapp)

# 确保是二维数组 (M,6)，每行一个样本
xapp = np.array(xapp)
yapp = np.array(yapp)
# 强制标签为 {1, -1}
yapp = np.where(yapp == 1, 1, -1)
print("数据集大小:")   
print("样本个数" +str(len(xapp)))
print("标签个数" +str(len(yapp)))

4.2从数据集中随机提取训练样本和测试样本

随机提取5000条索引作为训练集，其余的作为测试集，测试集和训练集不应当有重合，否则可能导致测试结果被高估。

########################################################################
# 2、随机提取训练样本和测试样本
# 总样本数和训练样本数

numberOfSamples = len(xapp)   # 样本数
# 生成随机排列索引,用于提取随机样本作为训练集
indexList = np.random.permutation(numberOfSamples)
print("随机排列索引:" + str(indexList))
print("随机排列索引长:" + str(len(indexList)))

numberOfSamplesForTraining = 5000

# 训练集索引（前5000个随机索引）
train_idx = indexList[:numberOfSamplesForTraining]
# 测试集索引（剩余的随机索引）
test_idx = indexList[numberOfSamplesForTraining:]

# 提取训练集和测试集
xTraining = xapp[train_idx, :]   # (5000, 6)
yTraining = yapp[train_idx]      # (5000,)
print("训练集特征维度:" + str(xTraining.shape))
print("训练集标签维度:" + str(yTraining.shape))

xTesting = xapp[test_idx, :]     # (M-5000, 6)
yTesting = yapp[test_idx]        # (M-5000,)
print("测试集特征维度:" + str(xTesting.shape))
print("测试集标签维度:" + str(yTesting.shape))

4.3数据归一化

数据归一化，可消除不同特征之间的量纲差异，让它们处于相同的数值范围，从而 加快模型收敛速度、提高模型精度，并避免某些特征因数值过大而主导模型。

同时需要注意归一化的时候必须使用训练集参数，让测试集和训练集处于"同一坐标系"。不可使用测试集参数，否则会导致测试数据的信息被提前泄露。

########################################################################
# 3、数据归一化（对训练集计算均值与标准差，然后用相同参数对测试集进行归一化）
avgX = np.mean(xTraining, axis=0)
stdX = np.std(xTraining, axis=0)
print("特征均值:" + str(avgX))
print("特征标准差:" + str(stdX))
# 避免除以零的情况
stdX[stdX == 0] = 1
xTraining = (xTraining - avgX) / stdX
xTesting = (xTesting - avgX) / stdX

4.4大范围搜索

在较大尺度范围下使用五折法寻找最佳的C和gamma参数

########################################################################
# 4、大范围搜索
# SVM 高斯核（RBF）参数搜索
# 核函数 K(x1,x2) = exp(-||x1-x2||^2 / gamma)
# 目标：通过交叉验证（5 折）找到使识别率最高的 C 和 gamma
# 首先在粗尺度上搜索 C 和 gamma（参考 "A practical Guide to Support Vector Classification"）

CScale = [-5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15] # C = 2.^CScale
gammaScale = [-15, -13, -11, -9, -7, -5, -3, -1, 1, 3] #gamma = 2.^gammaScale
C_List = [2**c for c in CScale]
gamma_List = [2**g for g in gammaScale]
print("C列表:" + str(C_List))
print("gamma列表:" + str(gamma_List))

# 训练查找最佳参数
maxRecognitionRate = 0
bestC = None
bestGamma = None
bestCIndex = -1
bestGammaIndex = -1

for i, C in enumerate(C_List):
    for j, gamma in enumerate(gamma_List):
        # 设置 SVM 参数
        param = f'-t 2 -c {C} -g {gamma} -v 5 -q'#-p quiet 模式，屏蔽输出
        # 交叉验证
        recognitionRate = svm_train(yTraining.tolist(), xTraining.tolist(), param)
        print(f"C={C} (index={i}), gamma={gamma} (index={j}), 识别率={recognitionRate}%")
        # 更新最佳参数及其索引
        if recognitionRate > maxRecognitionRate:
            maxRecognitionRate = recognitionRate
            bestC = C
            bestGamma = gamma
            bestCIndex = i
            bestGammaIndex = j

print(f"最佳参数: C={bestC} (index={bestCIndex}), gamma={bestGamma} (index={bestGammaIndex}), 识别率={maxRecognitionRate}%")

4.5根据大范围搜索结果进行精细搜索

在此前搜索到的最佳C和gamma基础上，在该参数的周边搜索是否存在更好的参数

########################################################################
# 5、根据搜索结果进行精细尺度搜索
n = 10  # 插值点数

# 在最佳刻度的前后插值，生成更细的刻度范围
minCScale = 0.5 * (CScale[max(0, bestCIndex-1)] + CScale[bestCIndex])
maxCScale = 0.5 * (CScale[min(len(CScale)-1, bestCIndex+1)] + CScale[bestCIndex])
newCScale = np.linspace(minCScale, maxCScale, n)    # 在该范围内生成 n 个均匀分布的刻度值
newC = [2**c for c in newCScale]

minGammaScale = 0.5 * (gammaScale[max(0, bestGammaIndex-1)] + gammaScale[bestGammaIndex])
maxGammaScale = 0.5 * (gammaScale[min(len(gammaScale)-1, bestGammaIndex+1)] + gammaScale[bestGammaIndex])
newGammaScale = np.linspace(minGammaScale, maxGammaScale, n)
newGamma = [2**g for g in newGammaScale]

print("精细搜索 C 列表:", newC)
print("精细搜索 gamma 列表:", newGamma)

# 精细搜索
maxRecognitionRate_fine = 0
bestC_fine = None
bestGamma_fine = None
bestCIndex_fine = -1
bestGammaIndex_fine = -1

for i, C in enumerate(newC):
    for j, gamma in enumerate(newGamma):
        # 设置 SVM 参数
        param = f'-t 2 -c {C} -g {gamma} -v 5 -q'#-p quiet 模式，屏蔽输出
        # 交叉验证
        recognitionRate = svm_train(yTraining.tolist(), xTraining.tolist(), param)
        print(f"[精细搜索] C={C} (index={i}), gamma={gamma} (index={j}), 识别率={recognitionRate}%")
        # 更新最佳参数及其索引
        if recognitionRate > maxRecognitionRate_fine:
            maxRecognitionRate_fine = recognitionRate
            bestC_fine = C
            bestGamma_fine = gamma
            bestCIndex_fine = i
            bestGammaIndex_fine = j
print(f"[精细搜索] 最佳参数: C={bestC_fine} (index={bestCIndex_fine}), gamma={bestGamma_fine} (index={bestGammaIndex_fine}), 识别率={maxRecognitionRate_fine}%")

# 使用精细搜索得到的最佳参数
finalC = bestC_fine
finalGamma = bestGamma_fine

4.6使用最佳参数训练最终模型并存储

使用上述训练得到的最佳参数训练出最终的模型并保存模型和测试集。

########################################################################
# 6、使用最佳参数在整个训练集上训练最终模型，并保存模型和测试数据
# 设置最终训练参数（不使用 -v）
param = f'-t 2 -c {finalC} -g {finalGamma} -b 1'#-b 1 启用概率估计,不启用-v交叉验证

# 在整个训练集上训练模型
model = svm_train(yTraining.tolist(), xTraining.tolist(), param)



# 拼接数据文件的绝对路径
model_save_path = os.path.join(current_dir, "final_model.model")
xTesting_save_path = os.path.join(current_dir, "xTesting.npy")
yTesting_save_path = os.path.join(current_dir, "yTesting.npy")

# 保存模型到文件
svm_save_model(model_save_path, model)
# 保存测试数据到文件（用 numpy 保存）
np.save(xTesting_save_path, xTesting)
np.save(yTesting_save_path, yTesting)
print("最终模型和测试数据已保存到文件。")

4.7测试所需头文件

from libsvm.svmutil import *
import os
import numpy as np

4.8加载模型与测试模型

加载模型、测试集，使用模型预测结果并统计预测准确率。

#############################
# 加载模型和测试数据进行测试

# 获取当前 py 文件所在目录
current_dir = os.path.dirname(os.path.abspath(__file__))
# 拼接数据文件的绝对路径
model_path = os.path.join(current_dir, "final_model.model")
xTesting_path = os.path.join(current_dir, "xTesting.npy")
yTesting_path = os.path.join(current_dir, "yTesting.npy")

# 加载模型
model = svm_load_model(model_path)
# 加载测试数据
xTesting = np.load(xTesting_path)
yTesting = np.load(yTesting_path)
print("加载测试数据，特征维度:" + str(xTesting.shape))
print("加载测试数据，标签维度:" + str(yTesting.shape))
# 在测试集上进行预测，启用概率输出
p_label, p_acc, p_val = svm_predict(yTesting, xTesting, model, '-b 1')
print("测试集预测完成。")
print("预测标签:", np.array(p_label))   # 模型对于测试集的预测标签，前面定义了draw和棋为+1，其余为-1，参考数据:[-1. -1. -1. ... -1.  1. -1.]

# 模型在测试集上的准确率[准确率, 均方误差, 相关系数的平方（衡量预测值与真实值的相关性）]  (99.37977099236642, 0.02480916030534351, 0.9341247848103147)
# 准确率Accuracy：测试集中预测正确的样本数 / 总样本数 × 100%。
# 均方差MSE：预测值与真实值之间差异的平方的平均值，反映了预测误差的大小。MES=1/n * Σ(预测值 - 真实值)²
#        衡量预测值与真实值的偏差大小。越接近 0 越好
# 相关系数的平方SCC： 衡量预测值与真实值之间线性关系的强度，取值范围为0到1，越接近1表示线性关系越强。
#                   R²= [Σ(预测值 - 预测值均值)(真实值 - 真实值均值)]² / [Σ(预测值 - 预测值均值)² * Σ(真实值 - 真实值均值)²]

print("预测准确率:", p_acc)

labels = model.get_labels()  # 获取模型的类别标签顺序
print("模型类别标签顺序:", labels)
# 每个样本属于各类别的概率值，shape=(样本数, 类别数)
# 在二分类时，每行通常是 [prob_negative, prob_positive]
# 打印出labels后可知，结构为[[样本1正类概率,样本1负类概率], [样本2正类概率,样本2负类概率], ...]
# [[1.00000000e-07 9.99999900e-01]
#  [1.02607786e-02 9.89739221e-01]
#  [1.00000000e-07 9.99999900e-01]
#  ...
#  [1.00000000e-07 9.99999900e-01]
#  [9.37231779e-01 6.27682214e-02]
#  [1.00000000e-07 9.99999900e-01]]
print("预测概率值:", np.array(p_val))   

4.9数据图形化展示

计算ROC曲线和AUC值以展示模型的效果

# 检查 p_val 是否为空且每行至少有两个元素
# 非空检测、检测p_val中的每一行是否为列表或数组且长度大于1
if p_val and all(isinstance(row, (list, np.ndarray)) and len(row) > 1 for row in p_val):
    pos_index = labels.index(1)   # 找到 +1 的索引
    print("正类(+1)在标签中的索引:", pos_index)
    prob_pos = np.array([row[pos_index] for row in p_val])# 找到正类的概率对于标签顺序[1, -1]，正类索引为0
else:
    raise ValueError("p_val 为空或格式不正确，无法提取正类概率。")

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import mplcursors
import plotly.graph_objects as go
from sklearn.metrics import roc_curve, auc

# 计算ROC曲线数据
# 输入yTesting真实标签，prob_pos为预测为正类的概率，pos_label=1表示正类标签为1
# 输出: fpr假正率, tpr真正率, thresholds阈值
# fpr=假正率(False Positive Rate)：将负类错误分类为正类的比例。计算公式为：FPR = FP / (FP + TN)
# tpr=真正率(True Positive Rate)：将正类正确分类为正类的比例，也称为召回率。计算公式为：TPR = TP / (TP + FN)
# thresholds=阈值：用于分类的不同阈值,当预测概率 ≥ 某个阈值时判为正类,随着阈值从高到低移动，你会得到一条从左下到右上的 ROC 曲线
fpr, tpr, thresholds = roc_curve(yTesting, prob_pos, pos_label=1)
# 计算AUC值
# AUC=Area Under the Curve，ROC曲线下的面积，衡量分类器性能的指标
# ROC曲线：横坐标为假正率FPR，纵坐标为真正率TPR，随着阈值变化绘制(FPR, TPR) 点的连线
# AUC=0.5:模型和随机猜测一样，没有区分能力
# AUC<0.5:模型表现比随机猜测还差(通常是正负类概率取反了)
# AUC=1.0:完美分类器，能完全区分正负类
roc_auc = auc(fpr, tpr)
print("AUC值:", roc_auc)

###################
# 本地交互式 ROC 曲线
plt.figure()    # 创建绘图窗口
# 以横坐标fpr，纵坐标tpr绘制ROC曲线，label中显示AUC值
line_Roc, = plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (area = {roc_auc:.5f})')
# 绘制一条对角线，表示随机分类器的性能
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')  # 随机分类器参考线
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")


# 添加交互功能
cursor = mplcursors.cursor(line_Roc, hover=True)

@cursor.connect("add")
def on_add(sel):
    idx = int(sel.index)   # 转成整数索引
    sel.annotation.set_text(
        f"FPR={fpr[idx]:.3f}\nTPR={tpr[idx]:.3f}\nThreshold={thresholds[idx]:.3f}"
    )
plt.show()

4.10最终训练效果

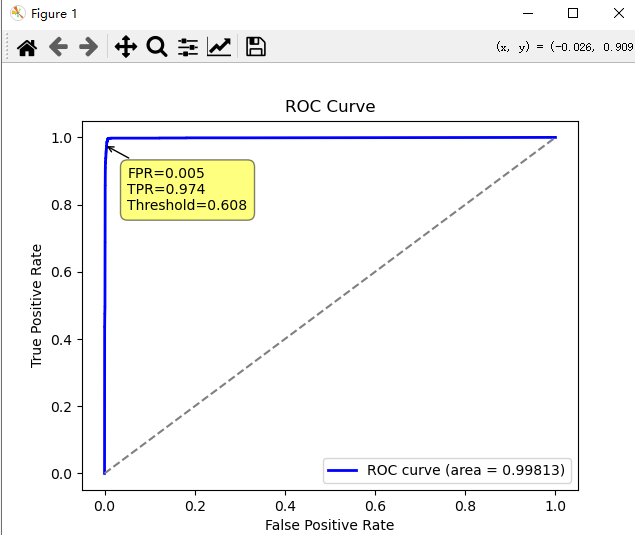
5、完整源码和数据集

完整源码和训练数据集已在github上给出，供您参考。
https://github.com/zaki-xie/ml-learning-lab/tree/main/SVM EXAPMLE/Pawn_King_Problem