
EKF 三维空间中,多维度的 强非线性 强非线性 强非线性滤波示例(位置 + 速度六维状态)
原创程序,非AI生成,保证运行成功,截图为实际运行结果
文章目录
程序概述
系统同时受到过程噪声影响,并可获得带噪声的三维位置与速度观测。为了在强非线性动力学下保持状态估计的稳定与精度,引入扩展卡尔曼滤波(EKF)对系统进行实时状态估计。
速度分量使用非线性的形式,构造强非线性,使得系统对状态变化更加敏感,适合验证 EKF 在复杂动力学下的表现。
示例程序提供:
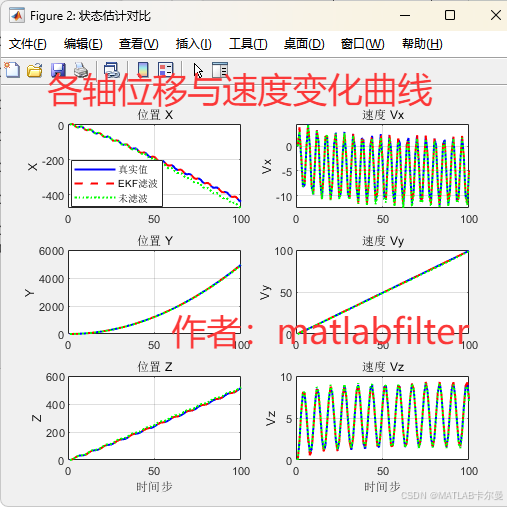
- 三维真实轨迹、未滤波轨迹、EKF 估计轨迹对比图
- 六个维度的位置与速度时间对比图
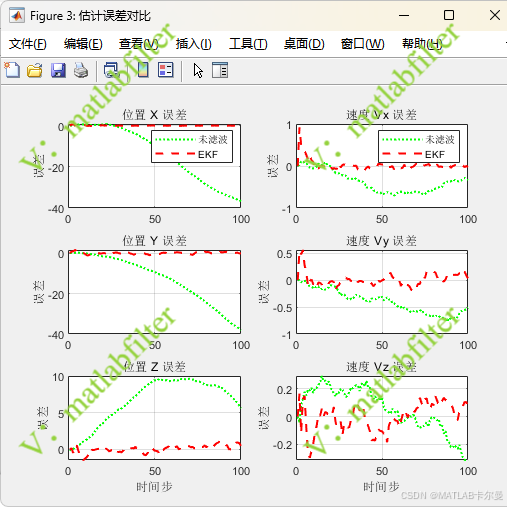
- 未滤波 vs EKF 的误差曲线
- 各维度绝对误差的 CDF 曲线
- 详细的误差统计输出(最大误差、均值、标准差)
运行结果
状态曲线(包括位置和速度):
对应的误差曲线:
部分代码:
程序结构:
MATLAB源代码
部分代码如下:
matlab
% EKF三维滤波(观测为三维速度和位置),强非线性状态方程,MATLAB例程
% 6维状态: [x, y, z, vx, vy, vz]'
% 作者:matlabfilter
% 2025-12-8/Ver1
clear; clc; close all;% 清除变量、命令行和图形窗口
rng(0); % 设置随机数种子
%% 模型初始化
t = 1:1:100; %设置时间序列
dt = 1; % 时间步长
% 状态向量: [x, y, z, vx, vy, vz]' (位置x, y, z, 速度vx, vy, vz)
Q = 0.01 * diag([0.5, 0.5, 0.5, 0.1, 0.1, 0.1]); % 过程噪声协方差矩阵 (6x6)
w = sqrt(Q) * randn(size(Q, 1), length(t)); % 过程噪声
R = 1 * diag([1, 1, 1, 0.5, 0.5, 0.5]); % 观测噪声协方差矩阵 (6x6) - 观测位置和速度
v = sqrt(R) * randn(size(R, 1), length(t)); % 观测噪声
P0 = 1 * eye(6); % 初始状态协方差矩阵 (6x6)
X = zeros(6, length(t)); % 真实状态 [x, y, z, vx, vy, vz]
X(:, 1) = [0; 0; 0; 0; 0; 0]; % 初始状态
X_ekf = zeros(6, length(t)); % 扩展卡尔曼滤波估计的状态
Z = zeros(6, length(t)); % 观测值 [x_obs, y_obs, z_obs, vx_obs, vy_obs, vz_obs]
Z(:, 1) = [X(1, 1)^2 / 20; X(2, 1); X(3, 1); X(4, 1); X(5, 1); X(6, 1)] + v(:, 1); % 设置观测量初值
%% 运动模型建立
X_ = zeros(6, length(t)); %给带误差的(未滤波的)状态量建立空间
X_(:, 1) = X(:, 1); %给带误差的状态量赋初值
for i1 = 2:length(t)
% 真实状态更新
% 位置更新: x = x + vx*dt, y = y + vy*dt, z = z + vz*dt
% 速度更新: vx, vy, vz根据非线性动力学更新完整代码下载链接:
https://download.csdn.net/download/callmeup/92445103
或:
如需帮助,或有导航、定位滤波相关的代码定制需求,请联系作者⬇️