这些概念听起来抽象,但其实就像"团队规模"和"个人耐力"一样简单。我来用通俗比喻、例子和图一步步解释。回忆一下:在椭圆曲线密码(ECC 椭圆曲线非对称加密的原理)中,一切建立在椭圆曲线的"点群"上,这个群用点加法运算,单位元是无穷远点O(像"零")。
1. 群的阶(Order of the Group)
- 定义:群的阶就是群里总共有多少个元素。简单说,是"这个团队有多大"。记作 |G| 或 #G。
- 在椭圆曲线中:椭圆曲线群E(所有满足方程的点 + O)的阶是 #E,约等于底层域的大小(比如GF(p)中p+1左右,但精确用Schoof算法算)。
- 例子:假如一个小型椭圆曲线在GF(5)上,有9个点(包括O),那么群的阶是9。实际ECC中,#E超级大(如2^256左右)。
- 为什么重要:阶决定群的"容量",在密码中要大且有大素因子,避免攻击。
这个图展示了一个椭圆曲线群的点集,总点数就是群的阶:
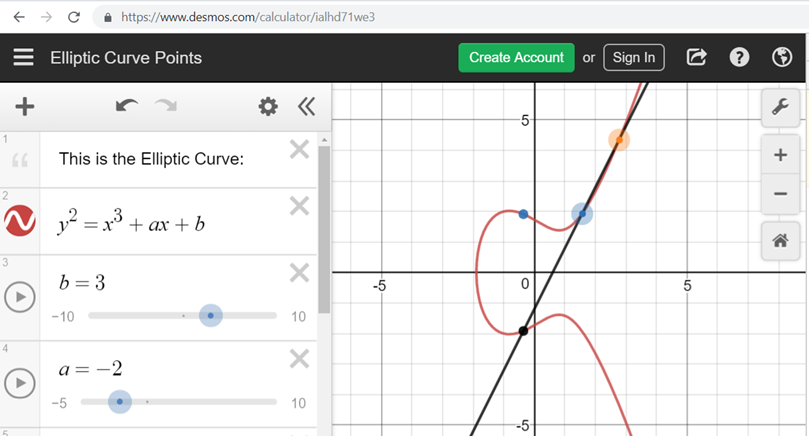
2. 元素的阶(Order of an Element)
- 定义:对于群里的一个元素g(比如一个点P),它的阶是最小的正整数k,使得k * g = O(单位元)。像"这个人能重复加多少次才回到起点"。
- 通俗比喻:想象P是"一步",走k步回到家,k就是阶。如果k=1,P就是O( trivial)。阶必须整除群的阶(拉格朗日定理)。
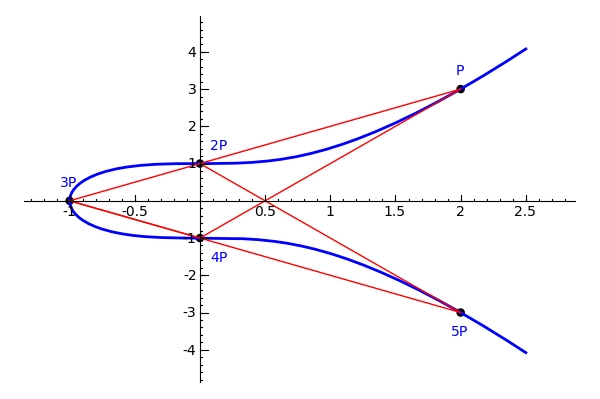
- 例子 :在上次的圆图中,P的阶是5,因为5P = O,但1P、2P、3P、4P都不等于O。计算时,从P开始加:2P = P+P,3P=2P+P...直到回到O。
- 在有限域:如果阶小,易攻击;密码中要大。
这里是一个点P的倍加过程,展示直到回到O的阶:
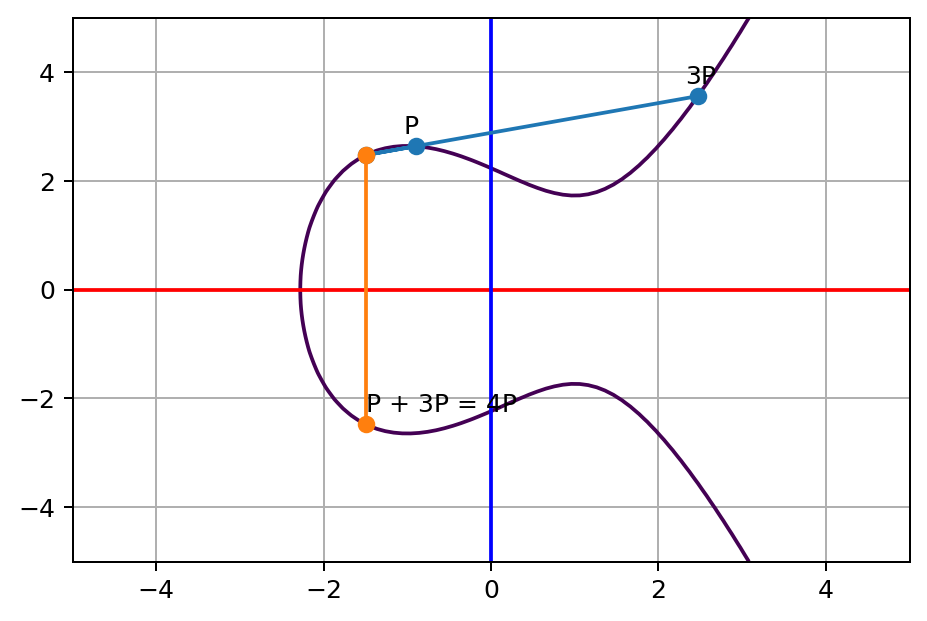
3. 基点G的阶(Order of the Base Point G)
- 定义:基点G是椭圆曲线群里的一个特殊点(生成元),它的阶n是最小正整数使得nG = O。n通常是子群的阶(G生成的循环子群的大小)。
- 区别:群的阶是整个E的规模,G的阶是G"子团队"的规模。G的阶n整除群的阶#E(往往n是#E的最大素因子)。
- 在ECC中:标准曲线如secp256r1,G的阶是巨大素数(~2^256),私钥d< n,公钥Q=dG。安全靠"求d难"(ECDLP)。
- 例子:比特币用secp256k1,G的阶n=115792089237316195423570985008687907852837564279074904382605163141518161494337。如果你算5G=O,阶=5(小例子)。
这个图说明从G开始倍加,找到阶的过程:
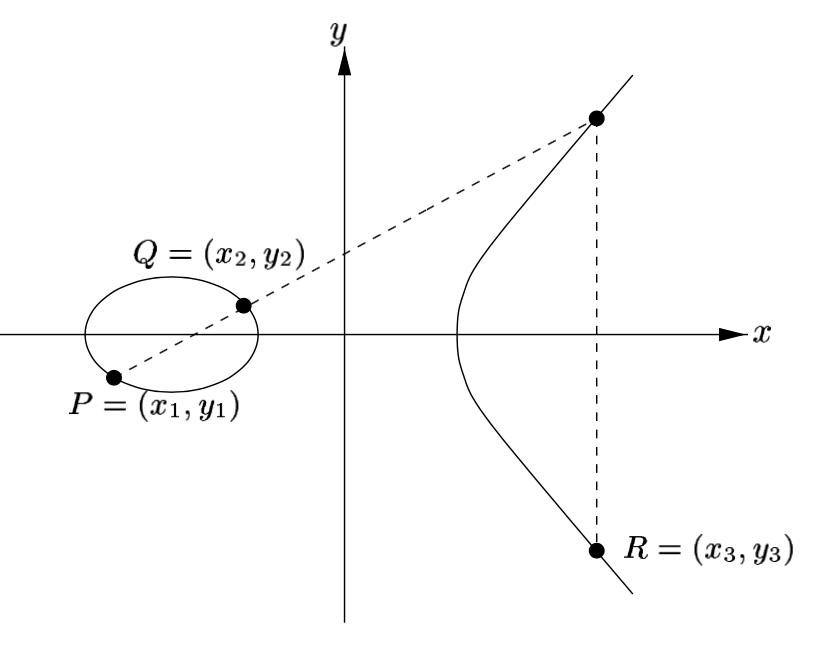
总结关系
- 群阶 |E|:总点数。
- 元素阶 ord(P):P到O的最小倍数。
- 基点G阶 n=ord(G):生成安全子群的规模。 就像大公司(群)、部门大小(子群阶)、员工轮班周期(元素阶)。在密码中,n大且素,确保安全。
计算基点G的阶的例子
先回顾一下:基点G的阶(order)是最小的正整数n,使得n × G = O(无穷远点)。这在椭圆曲线密码(ECC)中超级重要,因为n定义了私钥的范围(私钥d < n),并确保离散对数问题难解。
计算阶不是简单的事------对于大曲线如NIST P-256,需要复杂算法如Schoof的。但对于小型例子,我们可以用点倍加(scalar multiplication)来 brute-force:从1G开始计算2G、3G...直到回到O,计数步数。
示例:小型椭圆曲线上的计算
用一个简单曲线在有限域GF(23)上:y² = x³ + x + 1(其中p=23, a=1, b=1)。
选择基点G = (0, 1)。验证它在曲线上:1² mod23 = 0³ + 0 + 1 mod23 → 1=1,OK。
现在,计算倍点直到O:
- 1G = (0,1)
- 2G = 用点加法公式计算(细节:斜率m=(3x²+a)/(2y),新x=m²-2x 等,mod23)。
- ... 继续直到28G = O。
结果:G的阶n=28。这意味着子群有28个元素:{O, G, 2G, ..., 27G}。
通俗比喻:像转轮盘,转28次回到起点。实际中n很大(~2^256),手动算不可能,得用算法。
这里是一个椭圆曲线点阶计算的图解示例:
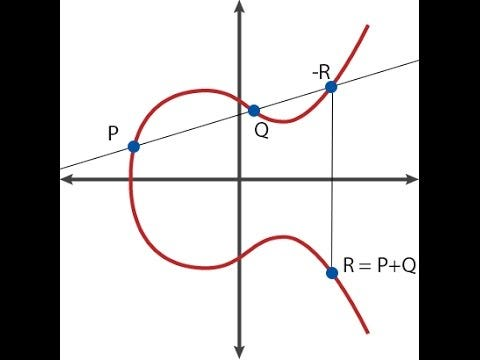
另一个展示点序计算的手写例子:
基点G的倍点坐标详细列表
在之前的例子中,我们使用了椭圆曲线 y2=x3+x+1y^2 = x^3 + x + 1y2=x3+x+1 在有限域 GF(23) 上(p=23,a=1,b=1)。基点 G = (0, 1),它的阶 n=28。这意味着由 G 生成的循环子群有 28 个元素:从 0G = O(无穷远点)到 27G,然后 28G 回到 O。
下面是完整的坐标列表,通过点倍加计算得到(使用椭圆曲线点加法公式,所有运算模 23)。我用表格呈现,便于阅读。每个 kG 的坐标 (x, y) 都满足曲线方程,且所有值在 0 到 22 之间。
| k | kG 坐标 |
|---|---|
| 0 | O (无穷远点) |
| 1 | (0, 1) |
| 2 | (6, 19) |
| 3 | (3, 13) |
| 4 | (13, 16) |
| 5 | (18, 3) |
| 6 | (7, 11) |
| 7 | (11, 3) |
| 8 | (5, 19) |
| 9 | (19, 18) |
| 10 | (12, 4) |
| 11 | (1, 16) |
| 12 | (17, 20) |
| 13 | (9, 16) |
| 14 | (4, 0) |
| 15 | (9, 7) |
| 16 | (17, 3) |
| 17 | (1, 7) |
| 18 | (12, 19) |
| 19 | (19, 5) |
| 20 | (5, 4) |
| 21 | (11, 20) |
| 22 | (7, 12) |
| 23 | (18, 20) |
| 24 | (13, 7) |
| 25 | (3, 10) |
| 26 | (6, 4) |
| 27 | (0, 22) |
| 28 | O (无穷远点) |
一些观察和解释
- 对称性:注意一些点如 1G=(0,1) 和 27G=(0,22),因为 22 ≡ -1 mod 23(-1 +23=22),所以 27G = -G(点的逆元是 (x, -y))。
- 中间点:如 14G=(4,0),y=0 表示这是一个2阶点(2*(4,0)=O),但在子群中它是14G。
- 循环:从 28G 回到 O,确认阶=28。实际计算中,我们用二进制展开的倍加算法(double-and-add)来高效计算,而不是逐一加。
- 验证示例 :取 2G=(6,19),检查方程:19² mod23=361 mod23=361-1523=361-345=16;右边6³ +6 +1=216+6+1=223 mod23=223-923=223-207=16。匹配!
- 在真实密码学曲线中(如 secp256r1),点数巨大,无法手动列出,但原理相同。