RobustMerge—— 无训练的 PEFT 模型融合方法，从低秩分解视角揭示方向鲁棒性对 PEFT 融合的作用

针对现有模型融合方法难以适配参数高效调优（PEFT，如 LoRA）模型、易出现任务干扰、泛化能力弱的问题，提出无训练的融合方法 RobustMerge，智能聚合多个基于同一主干的 PEFT 参数，在不增加额外模型层、不依赖训练数据和算力的前提下，让融合模型既保留各任务性能，又能泛化至未见过的任务，尤其适配多模态大模型的多任务融合需求。

它和 "传统单独的模型融合" 的核心区别 ------不是融合整个模型，而是融合模型里的 PEFT 小模块。

一、PEFT融合

1. LoRA模块分解：

LoRA（Low-Rank Adaptation）是PEFT的主流实现方式，通过两个低秩矩阵A、B的协同作用，为预训练大模型添加"任务专属功能"，核心逻辑为：

A矩阵："通用压缩工具"------将大模型的高维原始特征（如1000维图片特征）压缩为低维核心特征（如16维），参数分布均匀，作用不依赖具体任务，随机初始化也不影响核心性能。
B矩阵："专用调整工具"------将A矩阵输出的低维特征，转化为适配具体任务的特征格式（如"看图答题"需的"物体识别+答案匹配"特征），参数分布集中，核心参数直接决定任务性能，是PEFT模块的"能力核心"。
ΔW矩阵：A与B的乘积（ΔW=B×A），是承载"压缩+调整"完整逻辑的"功能成品"，也是后续分析与融合的核心对象，其秩代表任务知识的核心维度数量。

A 矩阵 "通用" 的原因：

作用不挑任务：A 矩阵都只负责 "压缩特征"，不会针对某个任务做特殊调整。不挑场景。

参数分布均匀：A 矩阵的参数数值都比较接近（比如大多在 - 0.1~0.1 之间），没有特别大或特别小的 "突出参数"。没有 "专精功能"。

训练时变化小：论文里提到，A 矩阵哪怕 "随机初始化不训练"，模型性能也不会差太多。就像万能扳手买回来不用改装，直接就能用，对最终效果影响不大。

B 矩阵 "专用" 的原因：

作用完全挑任务：如果任务是 "看图答题"，B 矩阵会专门把 A 压缩后的特征，调整成 "识别图片物体 + 匹配问题答案" 的格式；如果任务是 "写描述"，B 会调整成 "组织语言描述图片细节" 的格式。

参数分布集中：B 矩阵的参数里，会有几个 "数值特别大的参数"（比如 1.2、-1.5），这些参数对应 "任务的核心需求"（比如 "看图答题" 里 "匹配答案" 的参数）；其他参数数值很小，只是辅助。功能高度集中。

训练时变化大，决定性能：论文里强调，B 矩阵的训练效果直接决定任务性能 ------ 如果 B 矩阵没调好，哪怕 A 矩阵再好，模型也学不会新任务。

2. 奇异值分解（SVD）：PEFT的解析

SVD并非PEFT融合的目标，而是解析ΔW矩阵内部结构的关键工具，能将任意矩阵拆分为三个功能明确的组件：

左奇异向量U：对应ΔW处理知识的"逻辑方向"（如"先识别物体再匹配答案"），列向量彼此正交（独立无干扰）。
奇异值矩阵Σ：r×r对角矩阵（r为ΔW的秩），对角线上的数值（奇异值）代表对应方向的"知识重要性"，按从大到小排序，分别对应"核心知识"（头部奇异值）与"辅助知识"（尾部奇异值）。
右奇异向量V：负责整理特征格式，对PEFT融合的核心分析作用有限，通常可忽略。

通过SVD可清晰看到ΔW的"知识结构"------核心知识对应长向量（大奇异值），辅助知识对应短向量（小奇异值）。

3. SVD结果的融合可视化

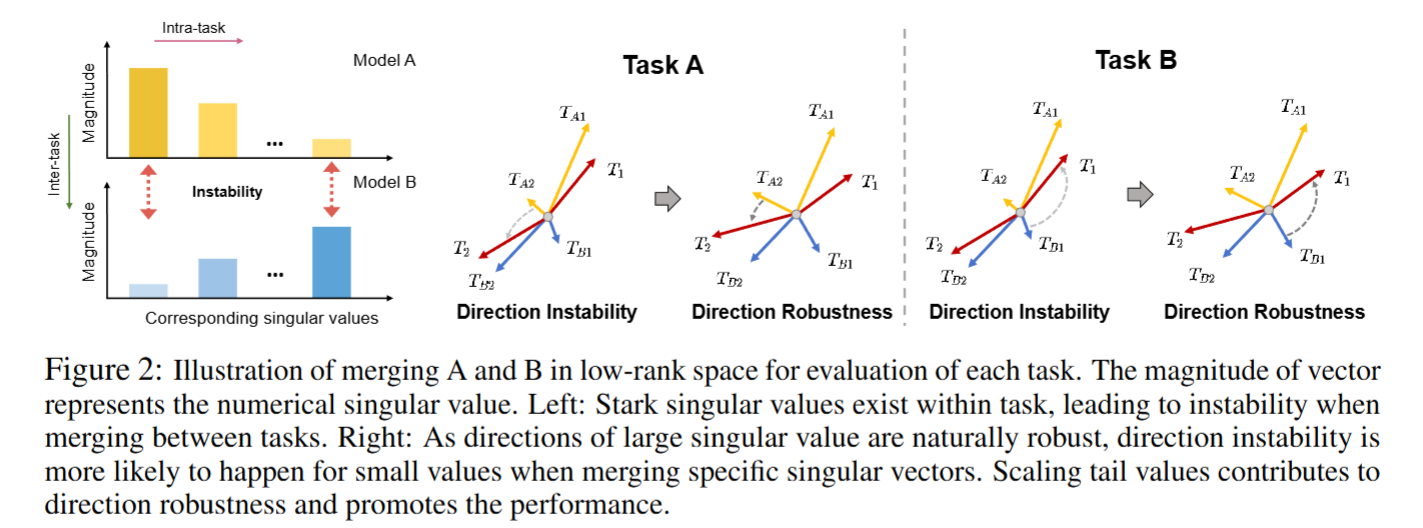
图中是RobustMerge方法的核心可视化证据，以"秩=2"为例，用向量直观展示PEFT融合的问题与解决方案：

向量含义：每种颜色的两个向量，代表某任务ΔW经SVD拆解后的"核心知识维度"（长向量，对应大奇异值）与"辅助知识维度"（短向量，对应小奇异值），向量方向=U的列向量方向，长度=Σ的奇异值大小。
左图（未处理）：奇异值差距极大（长向量极长，短向量极短），融合时辅助知识向量易被其他任务干扰而"方向跑偏"，导致性能下降。
右图（RobustMerge处理后）：通过参数调整缩小奇异值差距（短向量变长），辅助知识抗干扰能力增强，融合后核心与辅助知识方向均保持稳定，性能提升。

二、PEFT融合的痛点与传统方法的局限

PEFT模型融合的核心矛盾与全微调（FFT）模型完全不同，传统方法（如直接相加参数）无法适配，主要痛点包括：

方向不稳定：PEFT的ΔW矩阵奇异值差距极大（如头部=5，尾部=0.1），辅助知识向量（短向量）抗干扰能力弱，融合时易被其他任务的知识方向"带偏"，导致功能失效。
参数冲突难平衡：不同任务的PEFT模块参数规模与重要性差异大，直接融合易出现"数据多的任务权重霸占模型"的问题，无法兼顾多任务性能。
泛化能力弱：传统方法仅能适配训练过的任务，面对未见过的新任务时，因知识方向被破坏而性能暴跌。
工程成本高：部分融合方法需重新训练模型或依赖大量验证数据，落地效率低、算力消耗大。

三、RobustMerge的无训练融合逻辑

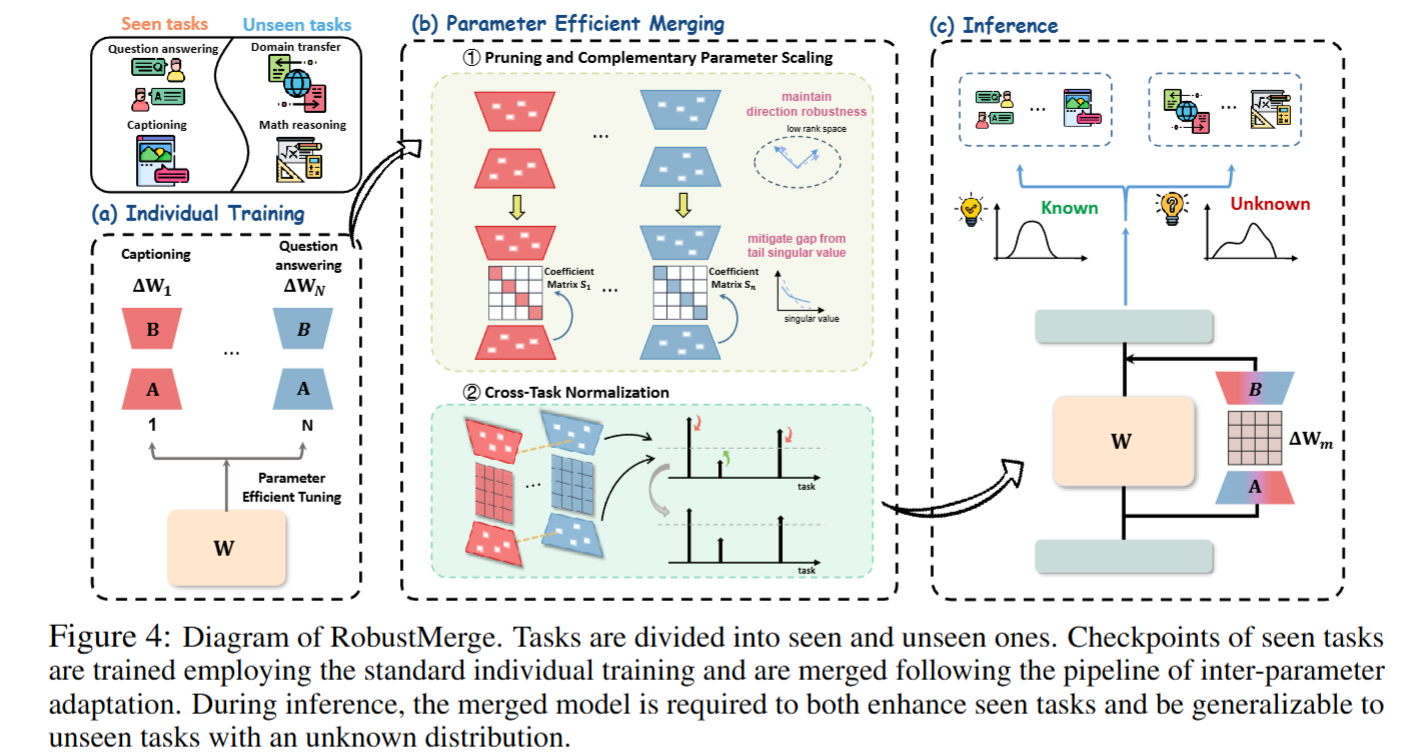
RobustMerge针对PEFT融合的核心矛盾，提出"以方向鲁棒性为核心"的无训练融合方案，通过三步固定数学规则实现高效聚合，全程无需训练数据：

1. 核心原则：维持方向稳定，平衡知识权重

基于SVD的理论发现，明确融合的关键是"缩小奇异值差距，保护U向量方向"------让核心知识与辅助知识均具备抗干扰能力，同时平衡不同任务的PEFT权重。

2. 逻辑实现

修剪无效参数：按参数幅度剔除各PEFT模块中数值极小的无效参数（如修剪率设为0.7，保留70%的大参数），直接缩小奇异值差距，减少垃圾参数的干扰。
互补参数缩放：基于LoRA的A矩阵统计特征计算缩放系数S（S=修剪前参数绝对值总和/修剪后总和），放大辅助知识参数的幅度，强化其抗干扰能力，对应图2中"短向量变长"的效果。

第一步：先对某个 LoRA 的 A 矩阵做修剪（比如保留 70% 的大参数，删掉 30% 的小参数）；

第二步：计算 "修剪前 A 矩阵某一行的参数绝对值总和"（比如第 1 行所有参数的绝对值加起来是 10）；

第三步：计算 "修剪后 A 矩阵同一行的参数绝对值总和"（比如修剪后剩下的参数绝对值加起来是 4）；

第四步：缩放系数 S = 修剪前总和 / 修剪后总和（比如 10/4=2.5）------ 意味着这个 LoRA 的 B 矩阵对应行的参数，要放大 2.5 倍（弱参数被强化）。
跨任务归一化：计算所有PEFT模块的缩放系数总和，以"自身S/总和"作为归一化系数，平衡不同任务的权重，避免数据规模差异导致的性能倾斜（如A任务S=5，B任务S=3，归一化后权重分别为0.625和0.375）。

3. 最终聚合公式

某任务PEFT的聚合后参数 = （修剪后A×修剪后B）× 互补缩放系数S × 跨任务归一化系数，所有任务参数相加后与原主干模型结合，即得到融合模型。