文章目录
当你迷茫的时候,请回头看看 目录大纲,也许有你意想不到的收获
一元线性回归
一元线性回归 函数表达式如下,其中 i 为样本序号:
z i = w x i + b z_i=wx_i+b zi=wxi+b
特点:一枝独秀
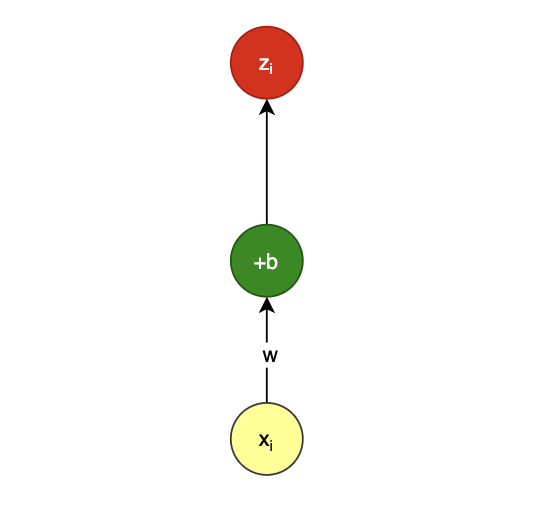
也可以写成 多元线性回归 的形式:
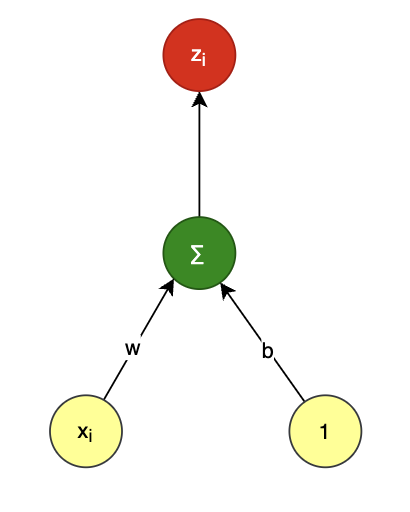
全部样本用矩阵表示如下,m 为样本总数:
z 1 z 2 ... z m \] = \[ x 1 1 x 2 1 ... ... x m 1 \] \[ w b \] \\begin{bmatrix} z_1\\\\\[10pt\] z_2\\\\\[10pt\] \\dots\\\\\[10pt\] z_m\\\\\[10pt\] \\end{bmatrix} =\\begin{bmatrix} x_{1} \& 1 \\\\\[10pt\] x_{2} \& 1 \\\\\[10pt\] \\dots \& \\dots\\\\\[10pt\] x_{m} \& 1\\\\\[10pt\] \\end{bmatrix} \\begin{bmatrix} w\\\\\[10pt\] b\\\\\[10pt\] \\end{bmatrix}\\\\\[10pt\] z1z2...zm = x1x2...xm11...1 wb 一切皆矩阵,令: X = \[ x 1 1 x 2 1 ... ... x m 1 \] m × 2 , W = \[ w b \] 2 × 1 , Z = \[ z 1 z 2 ... z m \] m × 1 X=\\begin{bmatrix} x_{1} \& 1 \\\\\[10pt\] x_{2} \& 1 \\\\\[10pt\] \\dots \& \\dots\\\\\[10pt\] x_{m} \& 1\\\\\[10pt\] \\end{bmatrix}_{m\\times 2}, W=\\begin{bmatrix} w\\\\\[10pt\] b\\\\\[10pt\] \\end{bmatrix}_{2\\times 1}, Z=\\begin{bmatrix} z_1\\\\\[10pt\] z_2\\\\\[10pt\] \\dots\\\\\[10pt\] z_m\\\\\[10pt\] \\end{bmatrix}_{m\\times 1} X= x1x2...xm11...1 m×2,W= wb 2×1,Z= z1z2...zm m×1 简记为: Z = X W Z=XW Z=XW ### 多元线性回归 特点: `根正苗红` ,多输入,单输出: 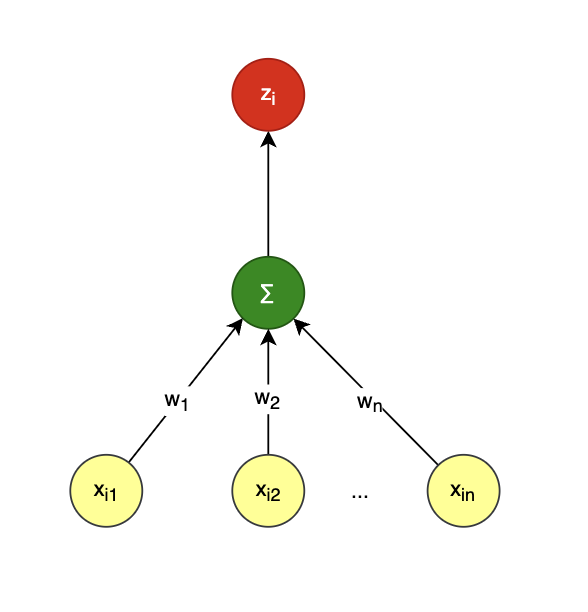 全部样本用矩阵表示如下,`m 为样本总数,n为多元输入数量`: \[ z 1 z 2 ... z m \] = \[ x 11 x 12 ... x 1 n x 21 x 22 ... x 2 n ... ... ... ... x m 1 x m 2 ... x m n \] \[ w 1 w 2 ... w n \] \\begin{bmatrix} z_1\\\\\[10pt\] z_2\\\\\[10pt\] \\dots\\\\\[10pt\] z_m\\\\\[10pt\] \\end{bmatrix} =\\begin{bmatrix} x_{11} \& x_{12} \&\\dots \& x_{1n}\\\\\[10pt\] x_{21} \& x_{22} \&\\dots \& x_{2n}\\\\\[10pt\] \\dots \& \\dots \&\\dots \& \\dots\\\\\[10pt\] x_{m1} \& x_{m2} \&\\dots \& x_{mn}\\\\\[10pt\] \\end{bmatrix} \\begin{bmatrix} w_1\\\\\[10pt\] w_2\\\\\[10pt\] \\dots\\\\\[10pt\] w_n\\\\\[10pt\] \\end{bmatrix}\\\\\[10pt\] z1z2...zm = x11x21...xm1x12x22...xm2............x1nx2n...xmn w1w2...wn 简记为: Z = X W Z=XW Z=XW ### 二分类逻辑回归 如果把 `线性加和` 看作是节, σ \\sigma σ 函数处理为枝,其特点是 `节外生枝`: 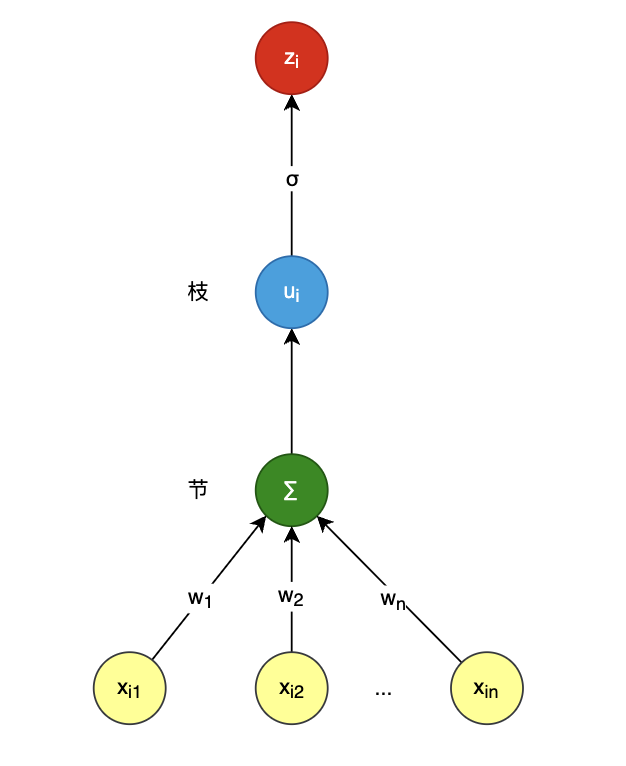 二分类是在多元线性回归基础上增加一个 σ \\sigma σ 函数得到 `概率输出` 全部样本用矩阵表示如下,`m 为样本总数`: \[ u 1 u 2 ... u m \] = \[ x 11 x 12 ... x 1 n x 21 x 22 ... x 2 n ... ... ... ... x m 1 x m 2 ... x m n \] \[ w 1 w 2 ... w n \] \\begin{bmatrix} u_1\\\\\[10pt\] u_2\\\\\[10pt\] \\dots\\\\\[10pt\] u_m\\\\\[10pt\] \\end{bmatrix} =\\begin{bmatrix} x_{11} \& x_{12} \&\\dots \& x_{1n}\\\\\[10pt\] x_{21} \& x_{22} \&\\dots \& x_{2n}\\\\\[10pt\] \\dots \& \\dots \&\\dots \& \\dots\\\\\[10pt\] x_{m1} \& x_{m2} \&\\dots \& x_{mn}\\\\\[10pt\] \\end{bmatrix} \\begin{bmatrix} w_1\\\\\[10pt\] w_2\\\\\[10pt\] \\dots\\\\\[10pt\] w_n\\\\\[10pt\] \\end{bmatrix}\\\\\[10pt\] u1u2...um = x11x21...xm1x12x22...xm2............x1nx2n...xmn w1w2...wn 简记为: U = X W U=XW U=XW z 与 u 的关系: z i = σ ( u i ) = 1 1 + e − u i z_i=\\sigma(u_i)=\\frac{1}{1+e\^{-u_i}} zi=σ(ui)=1+e−ui1 所以有 Z = \[ z 1 z 2 ... z m \] = \[ σ ( u 1 ) σ ( u 2 ) ... σ ( u m ) \] Z= \\begin{bmatrix} z_1\\\\\[10pt\] z_2\\\\\[10pt\] \\dots\\\\\[10pt\] z_m\\\\\[10pt\] \\end{bmatrix} =\\begin{bmatrix} \\sigma(u_1)\\\\\[10pt\] \\sigma(u_2)\\\\\[10pt\] \\dots\\\\\[10pt\] \\sigma(u_m)\\\\\[10pt\] \\end{bmatrix} Z= z1z2...zm = σ(u1)σ(u2)...σ(um) 简记为 Z = σ ( X W ) Z=\\sigma(XW) Z=σ(XW) ### 多分类逻辑回归 特点: `花开两朵,各表一枝` : 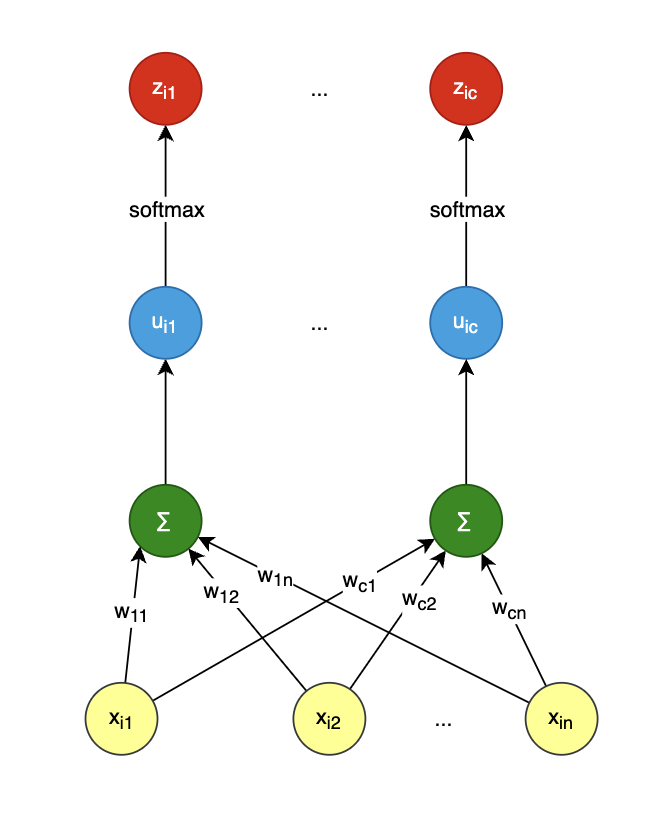 全部样本用矩阵表示如下,`m 为样本总数,c 为类别总数`: \[ u 11 u 12 ... u 1 c u 21 u 22 ... u 2 c ... ... ... ... u m 1 u m 2 ... u m c \] m × c = \[ x 11 x 12 ... x 1 n x 21 x 22 ... x 2 n ... ... ... ... x m 1 x m 2 ... x m n \] m × n \[ w 11 w 21 ... w c 1 w 12 w 22 ... w c 2 ... ... ... ... w 1 n w 2 n ... w c n \] n × c \\begin{bmatrix} u_{11}\& u_{12}\& \\dots\&u_{1c} \\\\\[10pt\] u_{21}\& u_{22}\& \\dots\&u_{2c} \\\\\[10pt\] \\dots\& \\dots\& \\dots\&\\dots \\\\\[10pt\] u_{m1}\& u_{m2}\& \\dots\&u_{mc} \\\\\[10pt\] \\end{bmatrix}_{m \\times c} =\\begin{bmatrix} x_{11} \& x_{12} \&\\dots \& x_{1n}\\\\\[10pt\] x_{21} \& x_{22} \&\\dots \& x_{2n}\\\\\[10pt\] \\dots \& \\dots \&\\dots \& \\dots\\\\\[10pt\] x_{m1} \& x_{m2} \&\\dots \& x_{mn}\\\\\[10pt\] \\end{bmatrix}_{m \\times n} \\begin{bmatrix} w_{11}\&w_{21}\&\\dots\&w_{c1}\\\\\[10pt\] w_{12}\&w_{22}\&\\dots\&w_{c2}\\\\\[10pt\] \\dots \&\\dots \&\\dots\&\\dots \\\\\[10pt\] w_{1n}\&w_{2n}\&\\dots\&w_{cn}\\\\\[10pt\] \\end{bmatrix}_{n \\times c}\\\\\[10pt\] u11u21...um1u12u22...um2............u1cu2c...umc m×c= x11x21...xm1x12x22...xm2............x1nx2n...xmn m×n w11w12...w1nw21w22...w2n............wc1wc2...wcn n×c 那么有 Z = \[ z 11 z 12 ... z 1 c z 21 z 22 ... z 2 c ... ... ... ... z m 1 z m 2 ... z m c \] = \[ f ( u 11 ) f ( u 12 ) ... f ( u 1 c ) f ( u 21 ) f ( u 22 ) ... f ( u 2 c ) ... ... ... ... f ( u m 1 ) f ( u m 2 ) ... f ( u m c ) \] Z=\\begin{bmatrix} z_{11}\& z_{12}\& \\dots\&z_{1c} \\\\\[10pt\] z_{21}\& z_{22}\& \\dots\&z_{2c} \\\\\[10pt\] \\dots\& \\dots\& \\dots\&\\dots \\\\\[10pt\] z_{m1}\& z_{m2}\& \\dots\&z_{mc} \\\\\[10pt\] \\end{bmatrix}= \\begin{bmatrix} f(u_{11})\& f(u_{12})\& \\dots\&f(u_{1c}) \\\\\[10pt\] f(u_{21})\& f(u_{22})\& \\dots\&f(u_{2c}) \\\\\[10pt\] \\dots\& \\dots\& \\dots\&\\dots \\\\\[10pt\] f(u_{m1})\& f(u_{m2})\& \\dots \&f(u_{mc}) \\\\\[10pt\] \\end{bmatrix} Z= z11z21...zm1z12z22...zm2............z1cz2c...zmc = f(u11)f(u21)...f(um1)f(u12)f(u22)...f(um2)............f(u1c)f(u2c)...f(umc) 其中 f 为 softmax 函数: f ( u i j ) = e u i j ∑ k = 1 c e u i k f(u_{ij})=\\frac{e\^{u_{ij}}}{\\sum\\limits_{k=1}\^{c}{e\^{u_{ik}}}} f(uij)=k=1∑ceuikeuij 简记为: U = X W Z = f ( U ) = f ( X W ) U=XW \\\\\[10pt\] Z=f(U)=f(XW) U=XWZ=f(U)=f(XW) 如果把 u 与 w 写成下面这种形式,i 为样本序号,j 为类别序号: z i = \[ z i 1 z i 2 ... z i c \] , u i = \[ u i 1 u i 2 ... u i c \] , w j = \[ w 11 w 21 ... w c 1 \] z_i=\\begin{bmatrix} z_{i1}\& z_{i2}\& \\dots\&z_{ic} \\end{bmatrix},\\\\\[10pt\] u_i=\\begin{bmatrix} u_{i1}\& u_{i2}\& \\dots\&u_{ic} \\end{bmatrix},\\\\\[10pt\] %% w_j=\\begin{bmatrix} w_{11}\&w_{21}\&\\dots\&w_{c1} \\end{bmatrix} zi=\[zi1zi2...zic\],ui=\[ui1ui2...uic\],wj=\[w11w21...wc1
那就与 二分类回归 中的这个表达式是一样的:
u 1 u 2 ... u m \] = \[ x 11 x 12 ... x 1 n x 21 x 22 ... x 2 n ... ... ... ... x m 1 x m 2 ... x m n \] \[ w 1 w 2 ... w n \] \\begin{bmatrix} u_1\\\\\[10pt\] u_2\\\\\[10pt\] \\dots\\\\\[10pt\] u_m\\\\\[10pt\] \\end{bmatrix} =\\begin{bmatrix} x_{11} \& x_{12} \&\\dots \& x_{1n}\\\\\[10pt\] x_{21} \& x_{22} \&\\dots \& x_{2n}\\\\\[10pt\] \\dots \& \\dots \&\\dots \& \\dots\\\\\[10pt\] x_{m1} \& x_{m2} \&\\dots \& x_{mn}\\\\\[10pt\] \\end{bmatrix} \\begin{bmatrix} w_1\\\\\[10pt\] w_2\\\\\[10pt\] \\dots\\\\\[10pt\] w_n\\\\\[10pt\] \\end{bmatrix}\\\\\[10pt\] u1u2...um = x11x21...xm1x12x22...xm2............x1nx2n...xmn w1w2...wn ### 神经网络 特点:`盘根错节` 提前预告一下,神经网络基础就是多分类回归,通过多层堆叠形成一个神经网络: 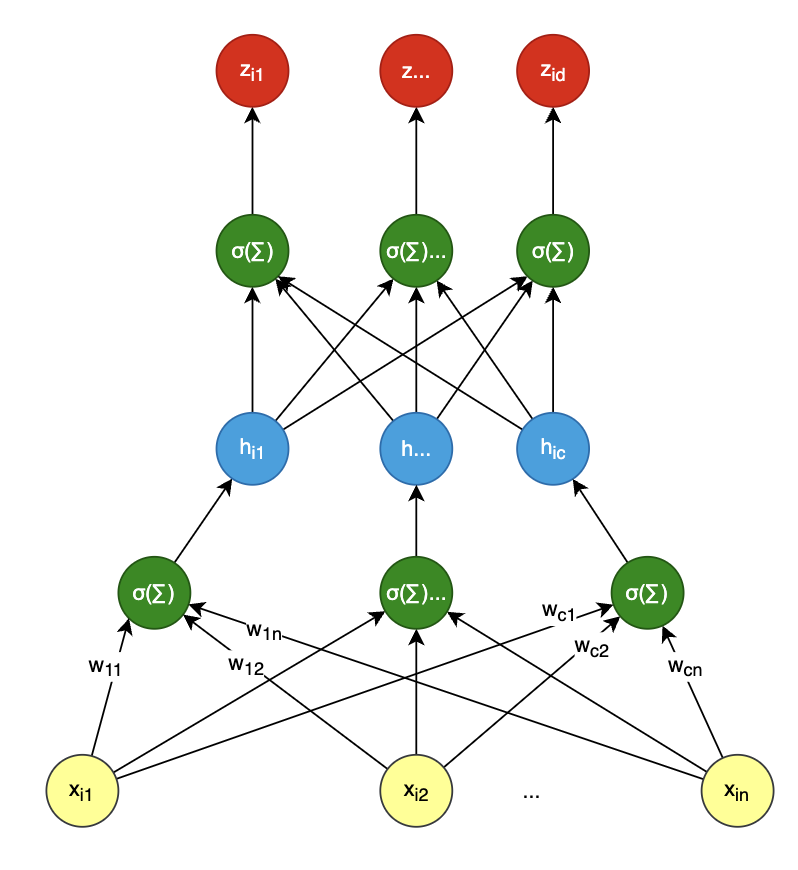 上面绿色的计算节点是把激活函数与线性求和整合到了一起,不然画不下了,例如: h i j = s i g n ( ∑ k = 1 n ( x i k w j k ) ) z i d = s i g n ( ∑ j = 1 c ( h i j v d j ) ) h_{ij}=sign{(\\sum\\limits_{k=1}\^{n}(x_{ik} w_{jk}))}\\\\\[10pt\] z_{id}=sign{(\\sum\\limits_{j=1}\^{c}(h_{ij} v_{dj}))} hij=sign(k=1∑n(xikwjk))zid=sign(j=1∑c(hijvdj)) `sign` 为符号函数,像前面 σ \\sigma σ 函数也是其中一种,还有 `RELU`,`tanh` 等等,主要就是给线性网络增加 `非线性` 因素,让神经网络可以模拟表达出非线性。 ### 总结 看看下面这幅汇总图,是否看到了一部进化史?就像人类进化一样,从直立人到智人再到现代人,功能越来越强大,结构也越来越复杂: 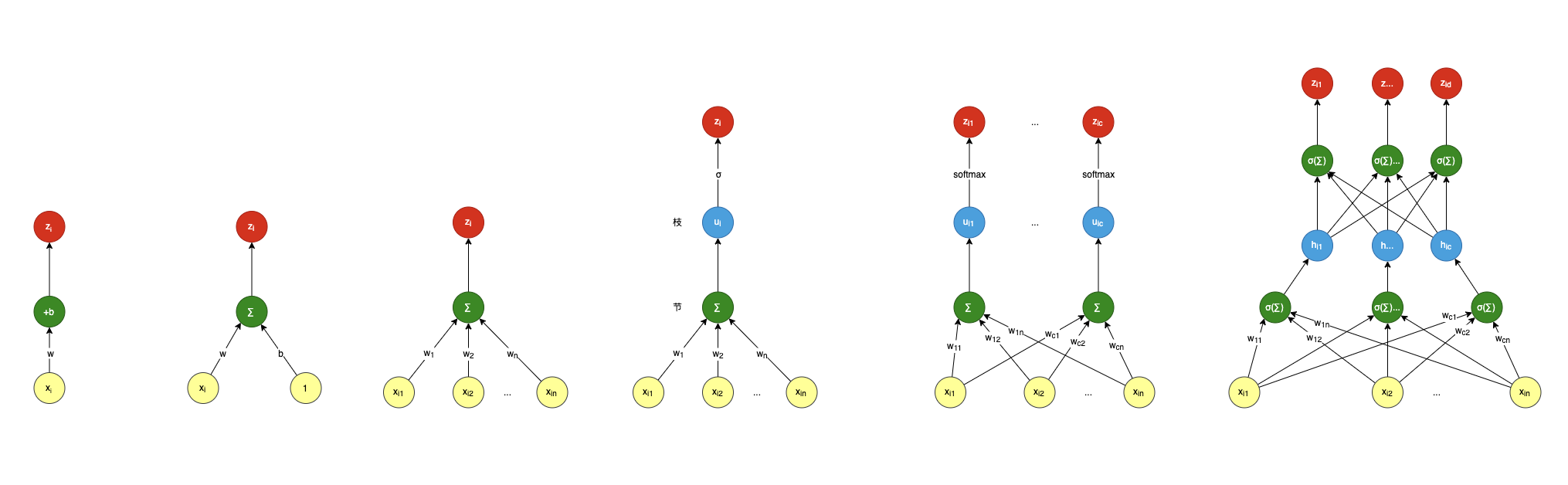  1. 从上述图中,我们看到它在一点点向复杂进化,开始 `单输入单输出` --\> `多输入单输出` --\> `多输入多输出`,一步一步,彼此之间又有关联与相似。 2. 从 `矩阵` 我们可以看出一些规律,输入 X 与输出 Z `矩阵行` 为样本,输入矩阵 X 的 `矩阵列` 为维度,输出矩阵 Z 的 `矩阵列` 为类别。