深度强化学习 TRPO 置信域策略优化实验（sb3_contrib / 手搓 + CartPole-v1 / Breakout-v5）

https://github.com/spy-ban/Reinforcement-Learning/tree/main/TRPO

1. sb3-contrib 调库快速搭建 TRPO 实验；

2. 从零实现 TRPO 的关键细节（KL 约束、共轭梯度、线搜索、GAE 等），

帮助深入理解算法本身的数学原理与工程实现。

本文深入解析了TRPO（Trust Region Policy Optimization）算法的核心实现，

并展示其在经典控制任务 CartPole-v1 和 Atari 游戏 Breakout-v5上的应用。

首先详细推导广义优势估计（GAE），阐释了其通过λ值平衡偏差与方差的原理。

随后重点拆解了 TRPO策略网络更新的关键步骤，包括构建代理目标函数、

计算Fisher信息矩阵 与 共轭梯度求解优化方向 ，以及使用回溯线搜索确定最优步长。

实验部分使用 stable-baselines3 库和手写TRPO代码进行验证：

在CartPole-v1上，手写实现仅用6000步即可稳定获得高分；

在Breakout-v5上，通过 CNN策略 与 多环境并行实现了高效训练。

文章为理解和复现TRPO这一经典信赖域算法提供了完整的理论梳理与代码实践参考。

目录

[1. GAE（Generalized Advantage Estimation）优势函数](#1. GAE（Generalized Advantage Estimation）优势函数)

[2. TRPO agent 网络更新](#2. TRPO agent 网络更新)

[2.1 策略网络参数更新](#2.1 策略网络参数更新)

[2.2 共轭梯度法求解优化方向：KL 散度关于策略参数的梯度](#2.2 共轭梯度法求解优化方向：KL 散度关于策略参数的梯度)

[2.3 优化步长：理论最长再不断减半验证](#2.3 优化步长：理论最长再不断减半验证)

[3. 实验](#3. 实验)

[3.1 用 sb3 的 TRPO 跑倒立摆](#3.1 用 sb3 的 TRPO 跑倒立摆)

[3.2 用 sb3 的 TRPO 跑 Breakout](#3.2 用 sb3 的 TRPO 跑 Breakout)

[3.3 手搓TRPO](#3.3 手搓TRPO)

---

1. GAE（Generalized Advantage Estimation）优势函数

• 蒙特卡洛 ：使用整个回合 的真实回报来估计。无偏，但高方差（因为后续所有随机动作和状态转移的噪声都包含在内）。

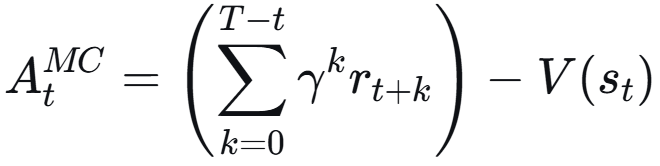
• 时序差分 ：使用一步奖励 和下一个状态的估计值 r + γV(s') - V(s)。低方差，但有偏（因为可能V(s')不准）。

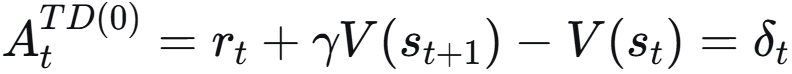
λ = 0，只看一步 则为 TD；λ = 1，看完整轨迹 蒙特卡洛；调 λ 平衡偏差与方差。

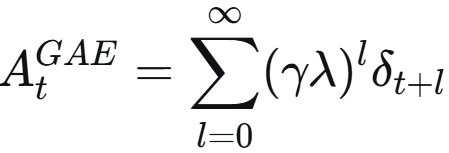
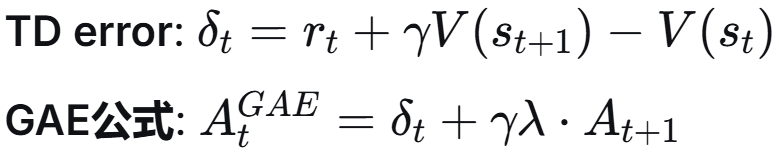
倒序循环累积

def gae(
    self,
    value_net: torch.nn.Module,
    states: torch.Tensor,
    rewards: torch.Tensor,
    next_states: torch.Tensor,
    not_dones: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    """输出每个时间步的折扣回报和优势函数值"""
    values = value_net(states)
    n = len(rewards)
    
    # 预分配输出张量
    Rs = torch.empty_like(rewards)
    advantages = torch.empty_like(rewards)
    
    # 初始化累计值
    next_val = value_net(next_states[-1])
    ret, adv = next_val, 0.0 # 上一个累积的 价值/优势函数
    
    for i in reversed(range(n)):
        not_done = not_dones[i]
        
        # 计算回报
        ret = rewards[i] + self.gamma * ret * not_done
        Rs[i] = ret
        
        # 计算优势函数
        td_error = rewards[i] + self.gamma * next_val * not_done - values[i]
        adv = td_error + self.gamma * self.lambda_ * adv * not_done
        advantages[i] = adv
        
        # 更新下一状态价值
        next_val = values[i]
    
    return Rs, advantages

2. TRPO agent 网络更新

总体：数据收集阶段 + 优势估计阶段 + 网络更新

算 Rs, gae 和两个网络更新。

def update(self) -> Dict: # 算 GAE 更新两个网络
    self.stats = dict()
    if self.trans_buffer.size >= self.cfg.agent.rollout_steps: # buffer满了则更新
        states, actions, next_states, rewards, dones = self.trans_buffer.buffers

        # get advantage
        with th.no_grad(): # 不计算梯度
            Rs, self.adv = self.gae(self.value_net, states, rewards, next_states, dones)

        self._update_actor(states, actions) # 更新策略网络
        self._update_value_net(states, Rs) # 更新价值网络

        self.trans_buffer.clear() # buffer更新完清空
    return self.stats

更新价值网络：与折扣回报的均方误差

def _update_value_net(self, states: th.Tensor, Rs: th.Tensor):
    idx = list(range(self.trans_buffer.size))
    for _ in range(self.cfg.agent.value_net.n_update):
        random.shuffle(idx)
        batches = list(BatchSampler(idx, batch_size=self.batch_size, drop_last=False))
        # 采样batch进行更新
        for batch in batches:
            sampled_states = states[batch]
            values = self.value_net(sampled_states)
            loss = F.mse_loss(values, Rs[batch]) # 价值网络与折扣回报的均方误差
            self.stats.update({"loss/critic": gradient_descent(self.value_net_optim, loss)})

2.1 策略网络参数更新

优化问题：确定优化方向 H^{-1}g 和 优化步长。

先准备损失函数的导数 和 kl 散度的导数。

重要性采样代理目标函数：

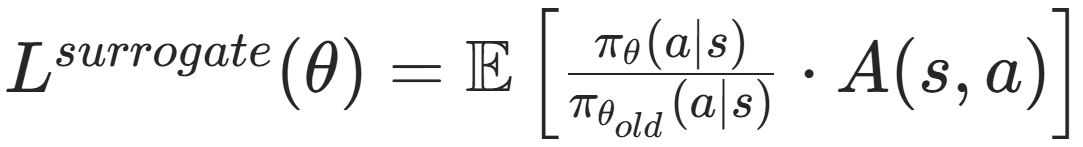
对数差的指数 -> 除法；加权优势函数期望 -> 均值

def _get_surrogate_loss(
    self, log_probs: th.Tensor, old_log_probs: th.Tensor
) -> th.Tensor:
    return th.mean(th.exp(log_probs - old_log_probs) * self.adv)

连续型 -> 高斯actor网络 mean, std = self.actor(states)

输入为状态 [batch_size, state_dim] -> 输出 动作的均值&标准差 [batch_size, action_dim]

如何求 π(a|s)：

输出：dist 每个动作的均值，方差 ；状态 s 下做这些动作 a 的对数概率（对数之和）

def _select_action_dist(
    self, states: th.Tensor, actions: th.Tensor
) -> Tuple[Normal, th.Tensor]: # 正态分布
    action_mean, action_std = self.actor(states)
    action_dist = Normal(action_mean, action_std)
    log_prob = th.sum(action_dist.log_prob(actions), dim=-1, keepdim=True) # 对数求和
    return action_dist, log_prob

正式策略网络参数更新：

准备损失函数的导数 和 kl 散度的导数 ，（锁定备份旧策略）

两个 graph -> True 便于后续求二阶导

def _update_actor(self, states: th.Tensor, actions: th.Tensor):
    original_actor_param = th.clone(parameters_to_vector(self.actor.parameters()).data) # 备份

    # 旧策略备份
    action_dist, log_probs = self._select_action_dist(states, actions)
    old_action_dist = Normal(action_dist.loc.data.clone(), action_dist.scale.data.clone())
    old_log_probs = log_probs.data.clone() # 旧策略old保存下来
    # 但后面求解时候 log_probs 会一直变

    # 定义损失函数的导数
    loss = self._get_surrogate_loss(log_probs, old_log_probs)
    pg = grad(loss, self.actor.parameters(), retain_graph=True)
    pg = parameters_to_vector(pg).detach()

    # 定义kl散度的导数
    kl = th.mean(kl_divergence(old_action_dist, action_dist))
    kl_g = grad(kl, self.actor.parameters(), create_graph=True)
    kl_g = parameters_to_vector(kl_g)

梯度方向 -> 最大 步长 -> 找最优 步长 -> 真的更新

理论最大步长 step_size = sqrt(2δ/(x^T H x))

    update_dir = self._conjugate_gradient(kl_g, pg)  # 共轭梯度求解梯度方向
    Fvp = self._Fvp_func(kl_g, pg)  # Hx
    full_step_size = th.sqrt(2 * self.delta / th.dot(update_dir, Fvp))  # 最大步长

    alpha = self._line_search(check_constrain)  # 最优步长
    vector_to_parameters(
        original_actor_param + alpha * full_step_size * update_dir,
        self.actor.parameters(),
    )  # 参数更新

2.2 共轭梯度法求解 优化方向：KL 散度关于策略参数的梯度

• 自然梯度方向 H^{-1}g，其中 H为 KL 散度的二阶 Fisher 信息矩阵，g为目标函数梯度

• 直接求逆计算量太大（O(n³)）使用共轭梯度法近似求解

  • 只需计算矩阵-向量乘积 Hv，不需要显式构造H

  • 迭代求解，直到残差足够小或达到最大步数

def _conjugate_gradient(self, kl_g: th.Tensor, pg: th.Tensor) -> th.Tensor:
    # 初始化：x为0向量，r和p初始化为梯度g
    x = th.zeros_like(pg)  # 解向量，初始为0
    r = pg.clone()         # 残差 r = b - Ax，初始为g（因为x=0时r=g）
    p = pg.clone()         # 搜索方向，初始为梯度方向
    rdotr = th.dot(r, r)   # r·r，用于计算收敛条件
    
    for _ in range(self.cg_steps):
        # Fisher 向量积 Hp
        _Fvp = self._Fvp_func(kl_g, p)
        
        # 计算步长 α = (r·r) / (p·Hp)
        alpha = rdotr / th.dot(p, _Fvp)
        
        # 更新解：x = x + αp
        x += alpha * p
        
        # 更新残差：r = r - αHp
        r -= alpha * _Fvp
        
        # 计算新的残差内积
        new_rdotr = th.dot(r, r)
        
        # 计算共轭系数 β = (r_new·r_new) / (r_old·r_old)
        beta = new_rdotr / rdotr
        
        # 更新搜索方向：p = r + βp
        p = r + beta * p
        
        # 更新残差内积
        rdotr = new_rdotr
        
        # 如果残差足够小，提前终止
        if rdotr < self.residual_tol:
            break
    
    return x  # 返回近似解 x ≈ H⁻¹g

ps：计算Fisher-向量乘积 Hp

• 通过自动微分计算Hp（二阶信息）、添加阻尼项提高数值稳定性

• 从 g 求导为 H，再乘以 p；变成对 （gp）求导

• 因为 g 是 d*1 向量；而 H 是 d*d 的，绕过存储 d*d 的 H

def _Fvp_func(self, kl_g: th.Tensor, p: th.Tensor) -> th.Tensor:
    
    # 1. 计算内积 g·p
    gvp = th.dot(kl_g, p)
    
    # 2. 对gvp求关于策略参数的梯度，得到Hp
    # 这是关键技巧：Hp = ∇(g·p)
    Hvp = grad(gvp, self.actor.parameters(), retain_graph=True)
    
    # 3. 将梯度列表展平为向量
    Hvp = parameters_to_vector(Hvp).detach()
    
    # 4. 添加阻尼项稳定数值计算
    # Hvp = Hp + λp，防止矩阵奇异
    Hvp += self.damping * p
    
    return Hvp

2.3 优化步长：理论最长再不断减半验证

回溯线搜索：从最大步长开始，按比例衰减

def _line_search(self, check_constrain: Callable) -> float: # 回溯线搜索
    alpha = 1.0 / self.beta
    for _ in range(self.max_backtrack):
        # 按比例衰减尝试
        alpha *= self.beta
        if check_constrain(alpha):
            return alpha
    return 0.0

check 验证这个步长可不可以

def check_constrain(alpha):
    step = alpha * full_step_size * update_dir
    with th.no_grad():
        vector_to_parameters(
            original_actor_param + step, self.actor.parameters()
        ) # 代入步长，得到假设参数更新后的新策略

        try: # 新策略的动作分布 + 概率（try 防止报错）
            new_action_dist, new_log_probs = self._select_action_dist(
                states, actions
            )
        except:
            vector_to_parameters(  # 报错啦！用备份的参数
                original_actor_param, self.actor.parameters()
            )
            return False
        new_loss = self._get_surrogate_loss(new_log_probs, old_log_probs) # 新损失
        new_kl = th.mean(kl_divergence(old_action_dist, new_action_dist)) # 新 KL
        actual_improve = new_loss - loss

    if actual_improve.item() > 0.0 and new_kl.item() <= self.delta:
        # 损失提升 且 KL≤阈值 -> 可以
        self.stats.update({"loss/actor": new_loss.item()})
        return True
    else:
        return False # 不行 继续改进

3. 实验

3.1 用 sb3 的 TRPO 跑倒立摆

TRPO-sb3-contrib

import gymnasium as gym
from sb3_contrib import TRPO
from stable_baselines3.common.evaluation import evaluate_policy

env = gym.make("CartPole-v1", render_mode="rgb_array")

model = TRPO(
    policy="MlpPolicy",
    env=env,
    learning_rate=3e-4,
    gamma=0.99,
    gae_lambda=0.95,
    verbose=1,
    n_steps=2048,
)

model.learn(total_timesteps=10000)  # 训练步数
model.save("trpo_cartpole_sb3")
model.env.close()

# 评估（无渲染）
eval_env = gym.make("CartPole-v1")
mean_reward, std_reward = evaluate_policy(model, eval_env, n_eval_episodes=10, deterministic=True)
print(f"Eval reward: {mean_reward:.1f} ± {std_reward:.1f}")
eval_env.close()

# 可视化测试
test_env = gym.make("CartPole-v1", render_mode="human")
loaded_model = TRPO.load("trpo_cartpole_sb3", env=test_env)

for ep in range(5):
    obs, _ = test_env.reset()
    ep_rew, done = 0.0, False
    while not done:
        action, _ = loaded_model.predict(obs, deterministic=True)
        obs, reward, terminated, truncated, _ = test_env.step(action)
        ep_rew += reward
        done = terminated or truncated
    print(f"测试轮 {ep+1} 总奖励: {ep_rew:.1f}")
test_env.close()

3.2 用 sb3 的 TRPO 跑 Breakout

ALE/Breakout-v5 弹小球打砖块，启动玩法 （需要先注册环境）

import gymnasium as gym
import ale_py

# 注册ALE的环境（必须步骤）
gym.register_envs(ale_py)
env = gym.make('ALE/Breakout-v5', render_mode='human')

obs, info = env.reset()

for _ in range(100):
    action = env.action_space.sample()
    obs, reward, terminated, truncated, info = env.step(action)
    if terminated or truncated:
        obs, info = env.reset()

env.close()

使用 Atari 经典预处理来优化 Breakout 训练效果：

- 图像预处理：灰度 + 缩放到 84x84（由 make_atari_env 内部包装）

- 帧堆叠：连续 4 帧作为输入（VecFrameStack）

- 奖励裁剪：clip_reward=True（内部包装）

- 多环境并行：n_envs > 1，加快采样，稳定梯度

import gymnasium as gym
import ale_py
from sb3_contrib import TRPO
from stable_baselines3.common.env_util import make_atari_env
from stable_baselines3.common.vec_env import VecFrameStack


# 注册 ALE 的环境（必须步骤）
gym.register_envs(ale_py)

n_envs = 4
env = make_atari_env(
    "ALE/Breakout-v5",
    n_envs=n_envs,
    seed=0,
    monitor_dir="./breakout_logs",  # 使用 Monitor 记录训练过程
    env_kwargs={"render_mode": "rgb_array"},  # 训练时不直接渲染窗口
)
env = VecFrameStack(env, n_stack=4)

TRPO 模型：Atari 为图像输入，需要使用 CNN 策略，训练100w步

model = TRPO(
    policy="CnnPolicy",  # 使用 CNN 策略处理图像输入
    env=env,
    learning_rate=1e-4,  # 稍小的学习率，训练更稳定
    gamma=0.99,
    verbose=1,
    target_kl=0.01,  # KL 散度约束目标值
    gae_lambda=0.95,  # 广义优势估计系数
    policy_kwargs=dict(normalize_images=False),
    n_steps=1024,
    batch_size=128,
    device="cuda",
    tensorboard_log="./trpo_breakout_tensorboard",
)

model.learn(total_timesteps=1000_000)
model.save("trpo_breakout_sb3")

测试

# 创建测试环境（与训练相同的预处理，但只用 1 个环境）
env_test = make_atari_env(
    "ALE/Breakout-v5",
    n_envs=1,
    seed=0,
    monitor_dir="./breakout_eval_logs",
    env_kwargs={"render_mode": "rgb_array"},
)
env_test = VecFrameStack(env_test, n_stack=4)

# 加载模型进行测试
loaded_model = TRPO.load("trpo_breakout_sb3", env=env_test)


# 测试模型（在 VecEnv 上评估）
for test_ep in range(20):
    obs = env_test.reset()
    test_reward = 0.0
    done = False
    steps = 0

    # 对于 VecEnv，done 是批量的布尔数组
    while (not done) and steps < 5000:  # 限制最大步数，避免无限循环
        # 确定性预测（关闭噪声，使动作更稳定）
        action, _states = loaded_model.predict(obs, deterministic=True)
        obs, rewards, dones, infos = env_test.step(action)

        # 单环境，索引 0 即可
        test_reward += float(rewards[0])
        done = bool(dones[0])
        steps += 1

    print(f"测试轮 {test_ep + 1} - 总奖励：{test_reward:.1f}, 步数：{steps}")

env.close()
env_test.close()

PowerShell 中启动 tensorboard

# tensorboard --logdir trpo_breakout_tensorboard --port 6006
# http://localhost:6006/ 网页看tensorboard

可视化 平均游戏长度 / 平均得分，上升趋势（还需要更多步数）：

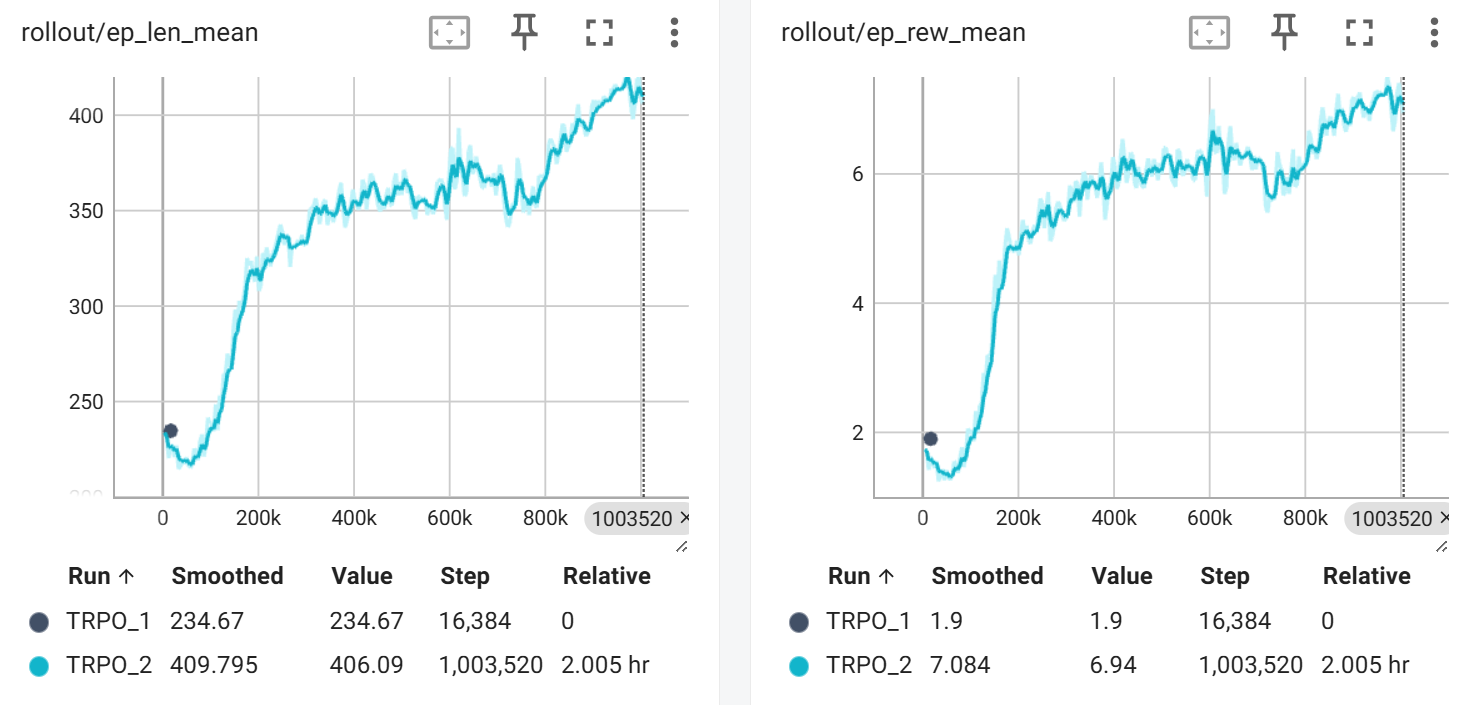
3.3 手搓TRPO

https://github.com/spy-ban/Reinforcement-Learning/tree/main/TRPO/TRPO-CartPole-v1

TRPO-CartPole-v1/

• agent.py：TRPO 算法核心逻辑（策略更新、Fisher 向量积、共轭梯度、线搜索等）
• networks.py ：自定义 Actor-Critic 网络结构（全连接 MLP）
• buffer.py ：采样数据缓冲区，实现交互数据的存储与张量化
• hyperparams.py ：TRPO_Config，集中管理超参数与设备选择
• train.py ：训练与测试流程（包含 GAE、early stopping、周期评估等逻辑）
• main.py ：入口脚本，一键训练并测试 TRPO 在 CartPole-v1 上的表现
• trpo_cartpole_custom.pth ：手写 TRPO 训练得到的模型权重

训练6000 timesteps 后即达到 475+ 均分（满分500）。