递归与分治算法

递归算法

递归算法（Recursion Algorithm）是一种重要的编程方法，核心思想是函数通过调用自身 来解决问题。在递归中，一个复杂的问题被分解为相同类型但规模更小的子问题，直到达到一个简单到可以直接解决的基本情况（基准情况）。递归算法特别适合解决具有自相似结构的问题，时间复杂度跟递归深度和每层处理的复杂度有关。

递归算法的妙处在于它能用简洁优雅的代码解决看似复杂的问题，但在使用时一定要注意避免无限递归和重复计算等问题。

算法步骤

定义递归函数，明确函数的功能和参数
确定递归的基准情况（终止条件）
将问题分解为更小的子问题
调用自身解决子问题
将子问题的结果组合起来，得到原问题的解

核心特性：

自我调用：函数在其定义中直接或间接调用自身
终止条件：必须有基准情况使递归能够终止
问题分解：将大问题分解为相同类型但规模更小的子问题
时间复杂度：与递归深度和每层处理的工作量相关
空间复杂度：受函数调用栈深度影响，通常与递归深度成正比

基础实现

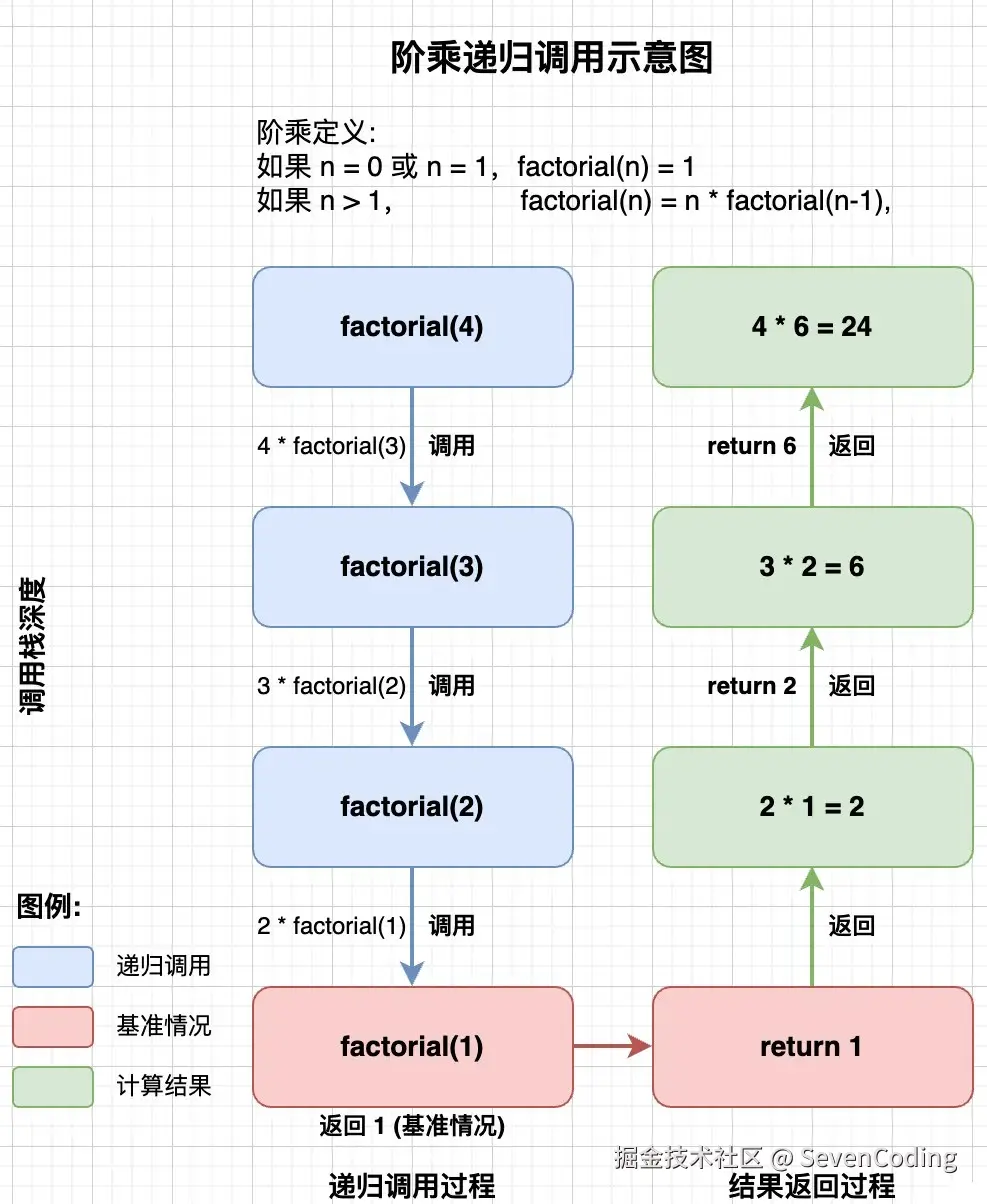
接下来通过阶乘（factorial）计算来展示递归算法的实现：

java 复制代码

public class Factorial {
    public static int factorial(int n) {
        // 基准情况
        if (n == 0 || n == 1) {
            return 1;
        }
        
        // 递归情况：n! = n * (n-1)!
        return n * factorial(n - 1);
    }
    
    // 测试
    public static void main(String[] args) {
        for (int i = 0; i <= 10; i++) {
            System.out.printf("%d! = %d
", i, factorial(i));
        }
    }
}

实现递归的核心思想，将计算 n! 的问题转化为计算 (n-1)! 的子问题。同时设置清晰的终止条件 if (n == 0 || n == 1) return 1; 确保递归能够结束。

优化策略

尾递归优化

通过将递归操作放在函数返回位置，可以被编译器优化，避免额外的栈空间消耗

java 复制代码

public static int factorialTailRecursive(int n) {
    return factorialHelper(n, 1);
}

private static int factorialHelper(int n, int accumulator) {
    // 基准情况
    if (n == 0 || n == 1) {
        return accumulator;
    }
    
    // 尾递归调用
    return factorialHelper(n - 1, n * accumulator);
}

记忆化递归

缓存已计算结果，避免重复计算

java 复制代码

public static int factorialMemoization(int n) {
    int[] memo = new int[n + 1];
    return factorialWithMemo(n, memo);
}

private static int factorialWithMemo(int n, int[] memo) {
    // 基准情况
    if (n == 0 || n == 1) {
        return 1;
    }
    
    // 检查是否已计算
    if (memo[n] != 0) {
        return memo[n];
    }
    
    // 计算并缓存结果
    memo[n] = n * factorialWithMemo(n - 1, memo);
    return memo[n];
}

优点

代码简洁优雅，易于理解和实现
适合处理树、图等具有递归结构的数据
某些问题用递归比迭代更直观（比如树的遍历）

缺点

函数调用开销较大，会影响性能
递归深度过大时可能导致栈溢出
重复计算子问题可能导致指数级时间复杂度
调试和跟踪执行流程较为困难
资源消耗（特别是栈空间）随递归深度增加

应用场景

1）数学计算：阶乘、斐波那契数列、组合数等 2）数据结构操作：树的遍历 、图的搜索（DFS） 3）分治算法：归并排序、快速排序 4）动态规划：子问题的递归求解 5）回溯算法：排列组合、八皇后、数独求解

分治算法

分治法(Divide and Conquer)是一种解决复杂问题的重要算法思想，其核心思想是将一个难以直接解决的大问题，分割成若干个规模较小的子问题，以便各个击破，最后将子问题的解组合起来，得到原问题的解。分治法的思想可以追溯到古代，但作为一种系统化的算法策略，它在计算机科学领域得到了极大的发展和应用。

算法步骤

分治算法通常遵循以下三个步骤：

分解(Divide)：将原问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。
解决(Conquer)：若子问题规模较小且容易解决则直接解决，否则递归地解各子问题。
合并(Combine)：将各子问题的解合并为原问题的解。

核心特性：

递归结构：分治算法通常使用递归实现，每个子问题继续分解直到达到基本情况
独立性：各子问题之间相互独立，不存在交叠
问题等价性：子问题与原问题形式相同，只是规模减小
合并操作：需要有效的合并子问题解的方法
基本情况处理：当问题规模小到一定程度，可以直接求解

优点

高效性：对于许多问题，分治算法能提供较高的效率
并行计算：分治算法天然适合并行计算，各子问题可以独立求解
模块化：问题划分为相互独立的模块，便于理解和实现
可复用性：同样的分治模式可以应用于多种问题求解

缺点

递归开销：递归调用会导致额外的函数调用开销和栈空间使用
内存使用：某些分治算法实现可能需要额外的内存空间
不适用性：不是所有问题都适合使用分治策略，尤其是子问题不独立的情况
合并难度：某些问题的子问题解合并起来可能相当复杂

应用场景

排序算法：归并排序、快速排序
搜索算法：二分搜索
矩阵运算：Strassen矩阵乘法
傅里叶变换：快速傅里叶变换(FFT)
最近点对问题：计算几何中的经典问题
大整数乘法：Karatsuba算法
棋盘覆盖问题：使用L型骨牌覆盖棋盘
图算法：最短路径、最小生成树等问题

递归与分治算法

递归算法

算法步骤

基础实现

优化策略

尾递归优化

记忆化递归

优点

缺点

应用场景

相关的 LeetCode 热门题目

分治算法

算法步骤

优点

缺点

应用场景

相关的 LeetCode 热门题目