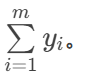🎬 博主名称 :个人主页
🔥 个人专栏 : 《算法通关》
⛺️心简单,世界就简单

引言
二分答案虽然说是作为基础算法,但二分这个思想是非常重要的,对于最小的最大值问题,最大的最小值问题,我们常常用到,所以我们接下来就进行题目练习
上一篇详细讲了这个基础算法,接下来我们通过一系列题来进行练习,掌握他
题目一
链接:寻找段落 - 洛谷 P1419 - Virtual Judge![]() https://vjudge.net/problem/%E6%B4%9B%E8%B0%B7-P1419
https://vjudge.net/problem/%E6%B4%9B%E8%B0%B7-P1419
题目展示
给定一个长度为 n 的序列 a,定义 ai 为第 i 个元素的价值。现在需要找出序列中最有价值的"段落"。段落的定义是长度在 [S,T]之间的连续序列。最有价值段落是指平均值最大的段落。
段落的平均值 等于 段落总价值 除以 段落长度。
Input
第一行一个整数 n,表示序列长度。
第二行两个整数 S 和 T,表示段落长度的范围,在 [S,T]之间。
第三行到第 n+2 行,每行一个整数表示每个元素的价值指数。
Output
一个实数,保留 3 位小数,表示最优段落的平均值。
Sample 1
输入
3
2 2
3
-1
2
输出1.000
【数据范围】
对于 30% 的数据有 n≤1000。
对于 100% 的数据有 1≤n≤100000,1≤S≤T≤n,−10^4≤ai≤10^4。
这道题主要是思考出来二分谁,以及理解如何利用单调队列解决求出窗口最小值问题
思路:
其实我最开始想的是对S T这个范围进行二分,然后这样长度就固定,然后check函数内容就是一个滑动窗口,但这样是不对的,S T是没有单调性的,不一定就是长度越长,平均数就越大,所以我们就不能这样,
我们可以取二分这个平均数,然后判断:是否存在长度在[s, t]之间的子数组,其平均值 ≥ mid
那么又一个问题来了如何判断平均值≥mid?
假设平均值 ≥ mid,那么:
-
子数组的元素都减去mid后,这个子数组的和 ≥ 0
-
即:存在长度在[s, t]之间的子数组,其元素减去mid后的和 ≥ 0
我们就可以 转换为前缀和问题
然后遍历前缀和数组,i 作为右端点,然后就变成了sum[i]-?这个值是大于等于mid,所以需要一个左端点,我们这时候可以用滑动窗口来维护数组某个片段的最小值,然后这个维护的方法就是传说中的单调队列。
这个窗口就是范围必须要在i-t到i-s范围,
cpp
#include<bits/stdc++.h>
using namespace std;
double a[100020];
int n,s,T;
double sum[100010];//前缀和数组
int q[100010];
bool check(double m){
int h=0,t=0;//h是head窗口的左边界,t是tail是窗口的右边界
//让每个数都减去m这个平均值,最后去利用前缀和判断这个区间是不是大于等于0就行
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i]-m;
for(int i=s;i<=n;i++){//i从s开始
//窗口保持着头是窗口的最小值,所以这个窗口是从小到大排序方式
//新进来的sum[i-s]如果比尾巴这个值小就让尾巴这个数出去(t--)
while(h<t&&sum[q[t-1]]>sum[i-s]) t--;
//让i-s 进来
q[t++]=i-s;
//窗口要始终保持在i-t,i-s范围
while(h<t&&q[h]<i-T) h++;
//如果遇到了平均数大于等于0的就直接返回1
if(h<t&&sum[i]-sum[q[h]]>=0) return 1;
}
return 0;
}
int main(){
cin>>n>>s>>T;
for(int i=1;i<=n;i++) cin>>a[i];
double l=-10000,r=10000;
while(0.000001<r-l){
//这是一个浮点数的二分答案
double m=(l+r)/2;
if(check(m)) l=m;
else r=m;
}
cout <<fixed<<setprecision(3)<<r<<endl;
return 0;
}题目二
链接:P1083 [NOIP 2012 提高组] 借教室 - 洛谷
题目展示
在大学期间,经常需要租借教室。大到院系举办活动,小到学习小组自习讨论,都需要向学校申请借教室。教室的大小功能不同,借教室人的身份不同,借教室的手续也不一样。
面对海量租借教室的信息,我们自然希望编程解决这个问题。
我们需要处理接下来 n 天的借教室信息,其中第 i 天学校有 ri 个教室可供租借。共有 m 份订单,每份订单用三个正整数描述,分别为 dj,sj,tj,表示某租借者需要从第 sj 天到第 tj 天租借教室(包括第 sj 天和第 tj 天),每天需要租借 dj 个教室。
我们假定,租借者对教室的大小、地点没有要求。即对于每份订单,我们只需要每天提供 dj 个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说我们要按照订单的先后顺序依次为每份订单分配教室。如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申请人修改订单。这里的无法满足指从第 sj 天到第 tj 天中有至少一天剩余的教室数量不足 dj 个。
现在我们需要知道,是否会有订单无法完全满足。如果有,需要通知哪一个申请人修改订单。
输入格式
第一行包含两个正整数 n,m,表示天数和订单的数量。
第二行包含 n 个正整数,其中第 i 个数为 ri,表示第 i 天可用于租借的教室数量。
接下来有 m 行,每行包含三个正整数 dj,sj,tj,表示租借的数量,租借开始、结束分别在第几天。
每行相邻的两个数之间均用一个空格隔开。天数与订单均用从 1 开始的整数编号。
输出格式
如果所有订单均可满足,则输出只有一行,包含一个整数 0。
否则(订单无法完全满足)输出两行,第一行输出一个负整数 −1,第二行输出需要修改订单的申请人编号。
输入
4 3
2 5 4 3
2 1 3
3 2 4
4 2 4
输出
-1
2
4 2 4输出 #1复制
-1 2说明/提示
【输入输出样例说明】
第 1 份订单满足后,4 天剩余的教室数分别为 0,3,2,3。第 2 份订单要求第 2 天到第 4 天每天提供 3 个教室,而第 3 天剩余的教室数为 2,因此无法满足。分配停止,通知第 2 个申请人修改订单。
【数据范围】
对于 10% 的数据,有 1≤n,m≤10;
对于 30% 的数据,有 1≤n,m≤1000;
对于 70% 的数据,有 1≤n,m≤105;
对于 100% 的数据,有 1≤n,m≤106,0≤ri,dj≤109,1≤sj≤tj≤n。
这个是读懂题目要的是第一个不满足的订单,而不是满足的,然后我们对二分时候要注意一下
思路:
这题其实刚开始看的时候没有理解为啥二分,咋二分,看了题解,发现是二分订单的单号,
仔细想了一下是这样的,如果你选择mid这个订单,发现从 l 到mid这些订单可以满足,按我们就往右找看看有没有不满足的,如果l到mid不满足那就往左看有没有还不满足的,因为咱要找第一个不满足的订单,然后这个看有没有不满足的是利用差分进行前缀和判断
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+10;
int n,m;
int sum[N],r[N],diff[N],d[N],s[N],t[N];
bool check(int mid){
memset(diff,0,sizeof(diff));
//对前mid个数进行差分处理
for(int i=1;i<=mid;i++) {
diff[s[i]]+=d[i];
diff[t[i]+1]-=d[i];
}
for(int i=1;i<=n;i++){
//开始判断有没有哪个订单已经不行了
sum[i]=sum[i-1]+diff[i];
if(sum[i]>r[i]) return 0;
}
return 1;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>r[i];
}
for(int i=1;i<=m;i++) cin>>d[i]>>s[i]>>t[i];
int l=1,r=m;
if(check(m)) {
cout<<0;
return 0;
}
while(l<=r){
int mid=(l+r)/2;
if(!check(mid)) r=mid-1;//这里注意,为啥是!
//因为我们题中要的是第一个不满足的订单
//所以就!
else l=mid+1;
}
//同样的这样输出,是因为r=mid-1造成不满足l<=r
cout<<-1<<"\n"<<l;
}题目三
链接: P2678 [NOIP 2015 提高组] 跳石头 - 洛谷
题目展示
一年一度的"跳石头"比赛又要开始了!
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
输入格式
第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证 L≥1 且 N≥M≥0。
接下来 N 行,每行一个整数,第 i 行的整数 Di(0<Di<L), 表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出格式
一个整数,即最短跳跃距离的最大值。
输入输出样例
输入
25 5 2
2
11
14
17
21
输出
4
这题不是很难,
思路:
这个跟上篇那个奶牛差不多,都是要找两个位置直接的最大的最小距离,所以我们就对距离进行二分,然后判断每两个石头之间距离是否满足这个最小距离,不满足就说明他俩之间距离太小,就直接把这个石头给扔了,然后继续判断下一个
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,L;
int x[50050];
bool check(int mid){
int last=0;//记录上一个石头的位置,开始时第一个石头在0位置
int num=0;
for(int i=0;i<=n;i++){
if(x[i]-last<mid) num++;//发现这个x[i]这个石头不满足最小距离,就把纸条搬走
else{
last=x[i];//更新上一次石头位置 ,即上一个石头的位置
}
if(num>m) return false;
}
return true;
}
signed main(){
cin>>L>>n>>m;
int l=0x3f3f3f3f,r=0;
for(int i=0;i<n;i++){
cin>>x[i];
}
x[n]=L;
l=1;
r=x[n]-0;//可能情况的最大值
while(l<=r){
int mid=l+(r-l)/2;
if(check(mid)){
l=mid+1;
}
else{
r=mid-1;
}
}
cout<<r;//这里输出r,因为最后l+1造成的不满足l<=r所以最后的正确的值是r而不是l
}题目四
链接:P1314 [NOIP 2011 提高组] 聪明的质监员 - 洛谷
题目展示
小 T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 n 个矿石,从 1 到 n 逐一编号,每个矿石都有自己的重量 wi 以及价值 vi。检验矿产的流程是:
- 给定 m 个区间 [li,ri];
- 选出一个参数 W;
- 对于一个区间 [li,ri],计算矿石在这个区间上的检验值 yi:
其中 j 为矿石编号,[p] 是指示函数,若条件 p 为真返回 1,否则返回 0。
这批矿产的检验结果 y 为各个区间的检验值之和。即:
若这批矿产的检验结果与所给标准值 s 相差太多,就需要再去检验另一批矿产。小 T 不想费时间去检验另一批矿产,所以他想通过调整参数 W 的值,让检验结果尽可能的靠近标准值 s,即使得 ∣s−y∣ 最小。请你帮忙求出这个最小值。
输入格式
第一行包含三个整数 n,m,s,分别表示矿石的个数、区间的个数和标准值。
接下来的 n 行,每行两个整数,中间用空格隔开,第 i+1 行表示 i 号矿石的重量 wi 和价值 vi。
接下来的 m 行,表示区间,每行两个整数,中间用空格隔开,第 i+n+1 行表示区间 [li,ri] 的两个端点 li 和 ri。注意:不同区间可能重合或相互重叠。
输出格式
一个整数,表示所求的最小值。
输入输出样例
输入 #1复制
5 3 15 1 5 2 5 3 5 4 5 5 5 1 5 2 4 3 3输出 #1复制
10说明/提示
【输入输出样例说明】
当 W 选 4 的时候,三个区间上检验值分别为 20,5,0,这批矿产的检验结果为 25,此时与标准值 S 相差最小为 10。
【数据范围】
对于 10% 的数据,有 1≤n,m≤10;
对于 30% 的数据,有 1≤n,m≤500;
对于 50% 的数据,有 1≤n,m≤5,000;
对于 70% 的数据,有 1≤n,m≤10,000;
对于 100% 的数据,有 1≤n,m≤200,000,0<wi,vi≤10^6,0<s≤10^12,1≤li≤ri≤n。
跟前面做的二分答案的题有一点点的差别,我们要灵活运用他
思路:
我们观察可以发现,W越大y就越小,W月小y就越大,我们就可以利用这个单调性,来二分W,然后找到答案
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=2e5+10;
LL n,m,s;
LL y,ans;
LL w[N],v[N];
int l[N],r[N];
LL cnt[N],sum[N];//两个前缀和数组
//cnt是记录前i个矿石重量>=W的个数
//sum是记录前i个重量>=W的矿石的总重
//这样每个区间[l,r]的简言之=(cnt[r]-cnt[l-1]) * (sum[r]-sum[l-1])
bool check(LL mid){
y=0;
memset(cnt,0,sizeof(cnt));
memset(sum,0,sizeof(sum));
for(int i=1;i<=n;i++){
if(w[i]>mid){
cnt[i]=cnt[i-1]+1;
sum[i]=sum[i-1]+v[i];
}
else{
cnt[i]=cnt[i-1];
sum[i]=sum[i-1];
}
}
for(int i=1;i<=m;i++){
int rr=r[i];
int ll=l[i];
y+=(cnt[rr]-cnt[ll-1])*(sum[rr]-sum[ll-1]);
}
if(y>s) return 1;//y>s说明W小了,咱想要接近s就让W大点,让下面 L=mid+1
return 0;
}
int main(){
cin>>n>>m>>s;
LL max_w=0;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
max_w=max(max_w,w[i]);
}
for(int i=1;i<=m;i++){
cin>>l[i]>>r[i];
}
LL L=1,R=1000020;
LL ans=0x3f3f3f3f3f3f3f3f;
while(L<=R){
int mid=(L+R)/2;
if(check(mid)){
L=mid+1;
}
else{
R=mid-1;
}
//比较一下刚才二分出来的y
ans=min(ans,llabs(s-y));
}
cout<<ans;
}题目五
题目展示
有一条奶牛冲出了围栏,来到了一处圣地(对于奶牛来说),上面用牛语写着一段文字。
现用汉语翻译为:
有 N 个区间,每个区间 x,y 表示提供的 x∼y 共 y−x+1 堆优质牧草。你可以选择任意区间但不能有重复的部分。
对于奶牛来说,自然是吃的越多越好,然而奶牛智商有限,现在请你帮助他。
输入格式
第一行一个整数 N。
接下来 N 行,每行两个数 x,y,描述一个区间。
输出格式
输出最多能吃到的牧草堆数。
输入输出样例
输入 #1复制
3 1 3 7 8 3 4输出 #1复制
5说明/提示
1≤n≤1.5×105,0≤x≤y≤3×106。
理解如何dp,以及本题为啥要以右端点排序
思路:
状态定义
dp[i] 表示考虑前 i 个区间(按右端点排序后),能够获得的最大牧草堆数。
为什么按右端点排序?
按右端点排序后,我们可以保证:
-
当我们考虑第 i 个区间时,所有可能与它重叠的区间都在它前面
-
这使得我们可以方便地找到最后一个不重叠的区间
对于每个区间 i,我们有两种选择:
情况1:不选第 i 个区间
如果我们不选区间 i,那么前 i 个区间的最优解就是前 i-1 个区间的最优解:
cpp
dp[i]=dp[i-1];//不选当前区间情况2:选第 i 个区间
如果我们选区间 i,那么:
-
我们不能选任何与区间 i 重叠的区间
-
我们需要找到最后一个右端点小于区间 i 左端点的区间 j
-
这样,区间 j 和它之前的所有区间都不会与区间 i 重叠
cppdp[i]=max(dp[i],dp[j]+interval[i].r-interval[i].l+1);cpp#include<bits/stdc++.h> using namespace std; #define int long long const int N=150010; struct Interval { int l,r; }interval[N]; int n; int rihghtend[N]; int dp[N]; bool cmp(const Interval& a,const Interval& b){ return a.r<b.r; } signed main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>interval[i].l>>interval[i].r; } //按右端点排序 sort(interval+1,interval+n+1,cmp); //记录排序后的右端点 for(int i=1;i<=n;i++){ rihghtend[i]=interval[i].r; } dp[0]=0; for(int i=1;i<=n;i++){ dp[i]=dp[i-1];//不选当前区间 int l=interval[i].l;//当前区间的左端点 //找到第一个 >=区间左端点的 // lower_bound找到第一个≥l的位置,减1就是最后一个<l的位置 int j=lower_bound(rihghtend+1,rihghtend+i,l)-rihghtend-1; dp[i]=max(dp[i],dp[j]+interval[i].r-interval[i].l+1); } cout<<dp[n]; }