决策树是一种直观且易于解释的监督学习算法,广泛应用于分类和回归任务。它通过模拟人类决策过程,将复杂问题拆解为一系列简单的判断规则,最终形成类似 "树" 状的结构。以下从基础概念、原理、算法类型、优缺点及应用场景等方面展开详细介绍。
概念
决策树通过对训练样本的学习,并建立分类规则,然后依据分类规则,对新样本数据进行分类预测,属于有监督学习
核心
所有数据从根节点一步一步落到叶子节点
根节点:第一个节点
非叶子节点:中间节点
叶子节点:最终结果节点
需要考虑的问题:
1.哪个节点作为根节点?哪些节点作为中间节点?哪些节点作为叶子节点?
2.节点如何分裂?
3.节点分裂标准的依据?
决策树的分类标准
1.ID3算法
衡量标准:
熵值:表示随机变量不确定性的度量,或者说是物体内部的混乱程度
熵值计算公式:

举例说明(数据如下图):
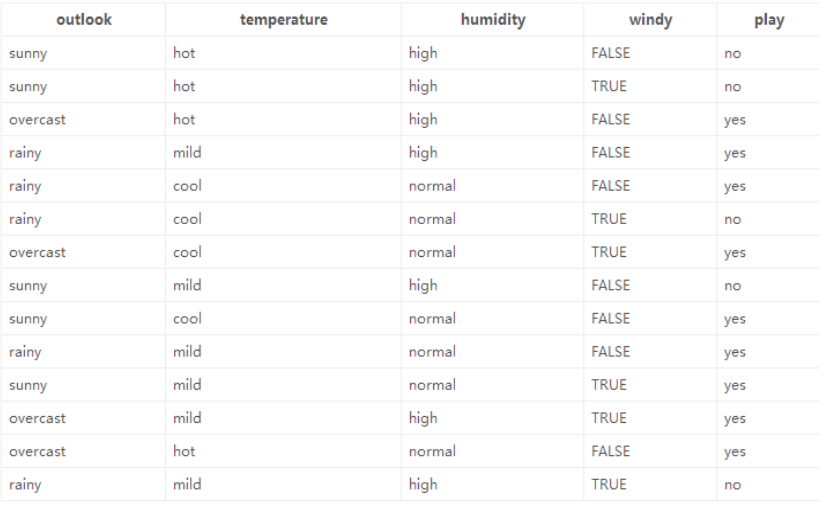
熵:熵值越小,该节点越"纯"。
第一遍遍历:
1.标签(结果是否外出打球)的熵(类别熵):
14天中,9天打球,5天不打球,熵为: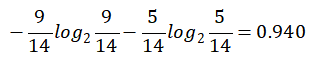
计算 对数的P ython程序 :
import math
result = -9/14*math.log(9/14, 2) - 5/14*math.log(5/14, 2)
2.基于天气的划分
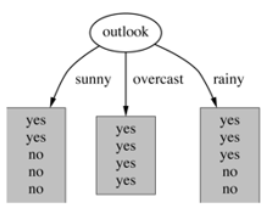
属性熵:
晴天【5天】的熵:
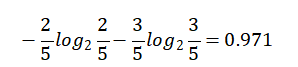
Overcast(阴天)【4天】的熵:
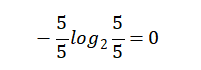
雨天【5天】的熵:
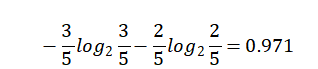
那么,天气对应标签结果的熵为:
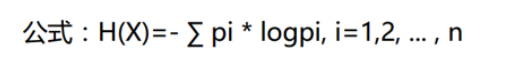
熵值计算:
5/14*0.971+4/14*0+5/14*0.971=0.693
则 信息增益为: 0.940-0.693 =0.247
在决策树算法中,信息增益(information gain)是特征选择的一个重要指标。它描述的是一个特征能够为整个系统带来多少信息量(熵),用于度量信息不确定性减少的程度。
如果一个特征能够为系统带来最大的信息量,则该特征最重要,将会被选作划分数据集的特征。
3.基于温度 的划分
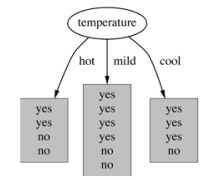
Hot【4天】的熵:
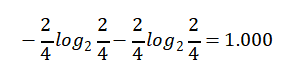
Mild【6天】的熵:
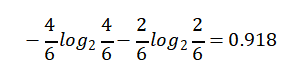
Cool【4天】的熵:
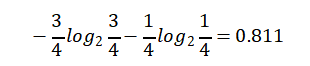
熵值计算:4/14*1+6/14*0.918+4/14*0.811=0.911
信息增益为:0.940 -- 0.911 = 0.029
4.基于湿度的划分
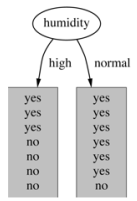
High【7天】的熵:
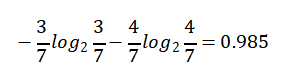
Normal【7天】的熵:
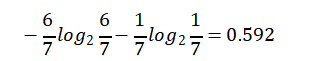
熵值计算:7/14*0.985+7/14*0.592=0.789
信息增益:0.940 -- 0.789 =0.151
5.基于有风的划分
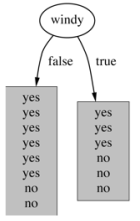
False【8天】的熵值:
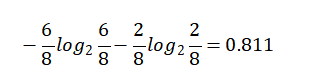
True【6天】的熵值:
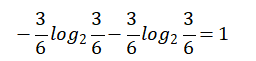
熵值计算:8/14*0.811 + 6/14*1 = 0.892
信息增益:0.940 - 0.892 = 0.048
综上:信息增益的大小:
天气:0.247
温度:0.029
湿度:0.151
有风:0.048
显然,信息增益最大的是: 天气 > 湿度 > 有风 > 温度
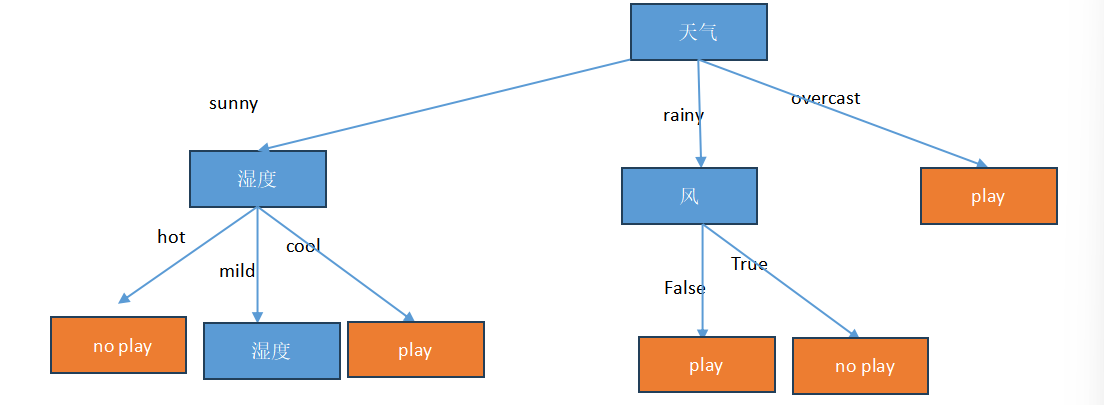
2.C4.5算法(解决稀疏向量的问题,例如编号)
衡量标准:信息增益率
C4.5算法是一种决策树生成算法,它使用信息增益比(gain ratio)来选择最优分裂属性,具体步骤如下:
1、计算所有样本的类别熵(H)。
2、对于每一个属性,计算该属性的熵【也为自身熵】(Hi)。
3、对于每一个属性,计算该属性对于分类所能够带来的信息增益(Gi = H - Hi)。
4、计算每个属性的信息增益比(gain ratio = Gi / Hi),即信息增益与类别自身熵的比值。
选择具有最大信息增益比的属性作为分裂属性。
3.CART决策树(用Gini指数最小化准则来进行特征选择。)
衡量标注:基尼系数
决策树剪枝
为什么要剪枝:
防止过拟合
如何剪枝:
预剪枝和后剪枝
通常进行预剪枝,因为后剪枝虽然精确度高,但是速度慢
预剪枝策略:
1.限制树的深度
2.限制叶子节点的个数以及叶子节点的样本树
3.基尼系数
决策树的优缺点
优点
简单直观,容易理解
不需要特征标准化
可处理离散和连续特征
对缺失值不敏感
可用于分类与回归
缺点
容易过拟合
对小样本数据不稳定
对类别不平衡敏感
可解释性好但精度可能不如集成方法(如随机森林、XGBoost)