LeetCode 分类刷题：110. 平衡二叉树

题目

给定一个二叉树，判断它是否是平衡二叉树

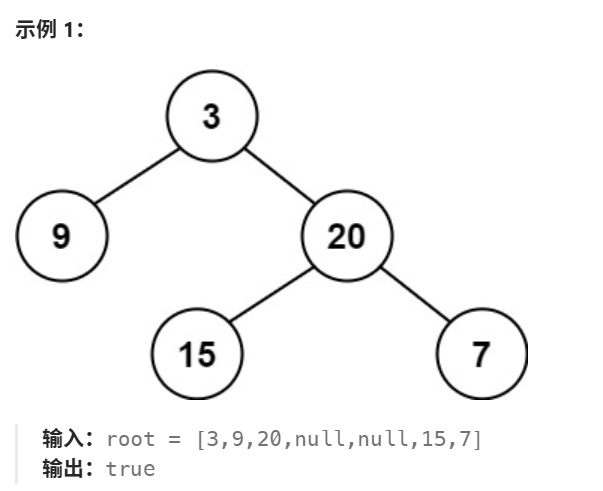
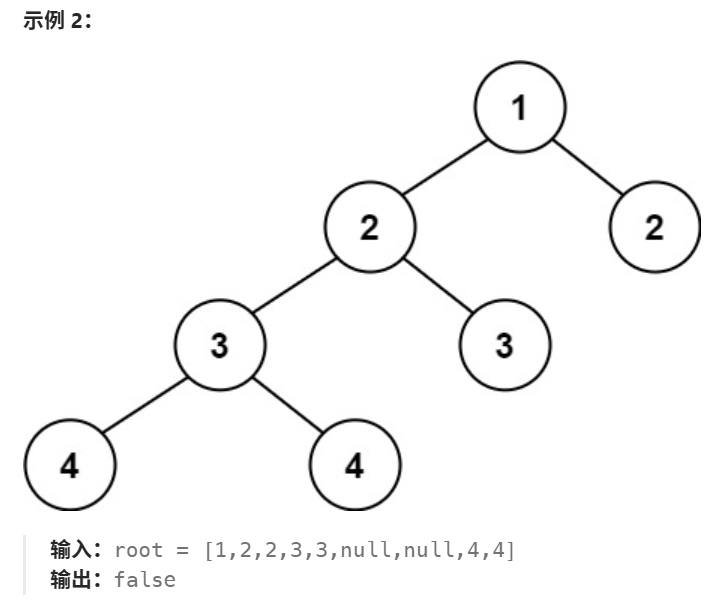
解析

// 怎么递归？

// 左右子树的高度相差不超过1

// 递归计算左、右子树的高度，如果高度相差超过1，返回-1；否则正常返回树的高度

// 递归终止条件：节点为空或已经检测出某棵子树不平衡

答疑

问：代码中的 −1 是怎么产生的？怎么返回的？

答：在某次递归中，发现左右子树高度绝对差大于 1，我们会返回 −1 。这个 −1 会一路向上不断返回，直到根节点。

作者：灵茶山艾府

链接：https://leetcode.cn/problems/balanced-binary-tree/solutions/2015068/ru-he-ling-huo-yun-yong-di-gui-lai-kan-s-c3wj/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

答案

这里一开始没写对，因为leftH 和 rightH没有声明类型！！！不止犯一次的错误了！！！

为什么必须加 let / const？

在 JavaScript 中，未声明的变量会成为全局变量（即使在函数内部）。
递归时，leftH 和 rightH 会被错误地覆盖（例如：第一次递归的 leftH 会污染后续递归的 leftH），导致高度计算错误。

javascript 复制代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function(root) {
    function f(node) {
        if(node === null) return 0;
        const leftH = f(node.left);
        if(leftH === -1) return -1;
        const rightH = f(node.right);
        if(rightH === -1 || Math.abs(leftH - rightH) > 1) return -1;
        return Math.max(leftH, rightH) + 1;
    }
    return f(root) !== -1;
};

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树的节点个数。

空间复杂度：O(n)。最坏情况下，二叉树退化成一条链，递归需要 O(n) 的栈空间。