PYTHON学习——决策树

决策树

概念

决策树通过对训练样本的学习，并建立分类规则，然后根据分类规则，对新样本数据进行分类预测，属于有监督学习。

核心

所有数据从根节点一步一步落到叶子节点。

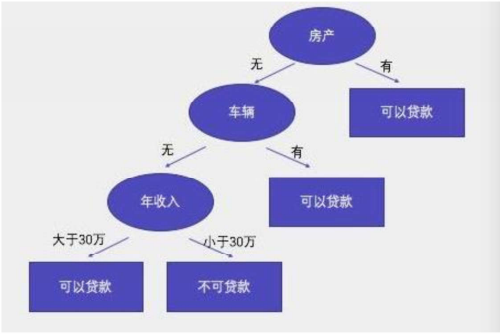
根节点：

第一个节点。

非叶子节点：

中间节点。

叶子节点：

最终结果节点。

决策树分类标准：

ID3算法

衡量标准：熵值：

表示随机变量不确定性的度量，或者说是物体内部的混乱程度。

计算公式：

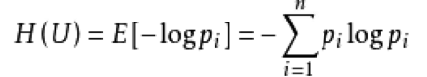
C4.5

定义

为解决信息增益的偏置问题，引入 "特征固有值" 做归一化：IGR(D,A)=IV(A)IG(D,A)其中 "固有值IV(A)" 是特征A的熵：IV(A)=−∑v=1V∣D∣∣Dv∣log2∣D∣∣Dv∣

核心逻辑

若特征A取值极多（如客户 ID），IV(A)会很大 → 信息增益比被 "惩罚"，避免无意义特征被选中；
信息增益比越大 → 特征划分效果越好。

基尼系数（Gini Index）------ CART 算法

定义

基尼系数衡量数据集的 "不纯度"，公式：Gini(D)=1−∑i=1npi2（pi：类别i的占比，基尼越小→纯度越高）

按特征A拆分后的基尼系数（加权平均）：Gini(D∣A)=∑v=1V∣D∣∣Dv∣Gini(Dv)

基尼增益（划分效果）：Gini_gain=Gini(D)−Gini(D∣A)

基尼增益越大 → 特征划分效果越好；
CART 树直接选择 "基尼系数最小的子节点组合" 对应的特征 + 阈值。

计算示例

同上述数据集：

原始基尼：Gini(D)=1−(104)2−(106)2=0.48
按 "月消费" 拆分后基尼：Gini(D∣A)=105∗(1−(54)2−(51)2)+105∗(1−0−1)=0.16
基尼增益：0.48−0.16=0.32

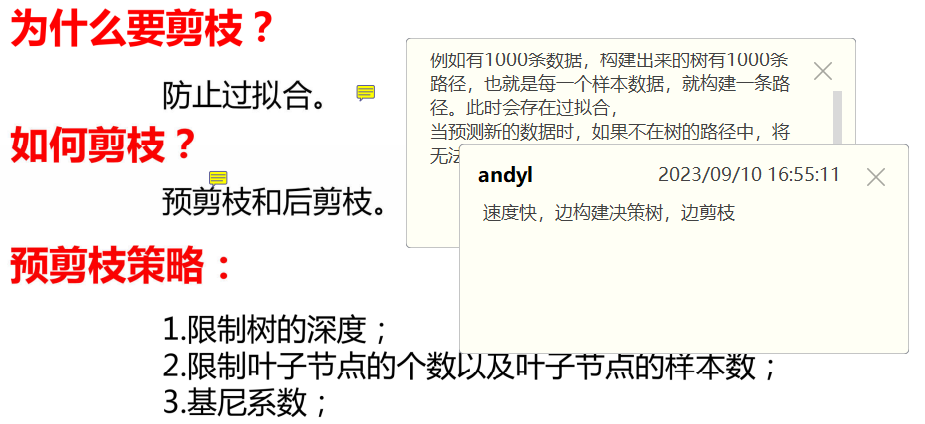
决策树剪枝

实例

python 复制代码

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.tree import plot_tree#决策树的绘图
from imblearn.over_sampling import SMOTE  # 导入SMOTE
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve, auc, roc_auc_score

def cm_plot(y,yp):
   from sklearn.metrics import confusion_matrix
   import matplotlib.pyplot as plt
   cm = confusion_matrix(y,yp)
   plt.matshow(cm,cmap=plt.cm.Blues)
   plt.colorbar()
   for x in range(len(cm)):
       for y in range(len(cm)):
          plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',verticalalignment='center')
          plt.ylabel('True label')
          plt.xlabel('Predicted label')
   return plt

df = pd.read_excel('电信客户流失数据.xlsx')
X = df.iloc[:, :-1]  # 所有特征列（除了最后一列）
y = df["流失状态"]   # 标签列

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y  # stratify保证类别分布一致
)

# 构建决策树分类器（针对流失预测调参）
dt_churn = DecisionTreeClassifier(
    criterion="gini",
    max_depth=12,  # 控制树深度，避免过拟合
    min_samples_split=18,
    random_state=42
)

# 训练+预测
dt_churn.fit(X_train, y_train)
y_pred = dt_churn.predict(X_test)
cm_plot(y_test,y_pred).show()
# 评估模型
print("准确率：", accuracy_score(y_test, y_pred))
print("\n混淆矩阵：")
print(confusion_matrix(y_test, y_pred))  # 看"流失客户"的预测准不准
print("\n分类报告：")
print(classification_report(y_test, y_pred))

# 计算特征重要性
feature_importance = pd.DataFrame({
    "特征": X.columns,
    "重要性": dt_churn.feature_importances_
}).sort_values(by="重要性", ascending=False)

print("特征重要性（前5名）：")
print(feature_importance.head())

fig, ax = plt.subplots(figsize=(32, 32)) #设置
plot_tree(dt_churn,filled = True, ax=ax)
plt.show()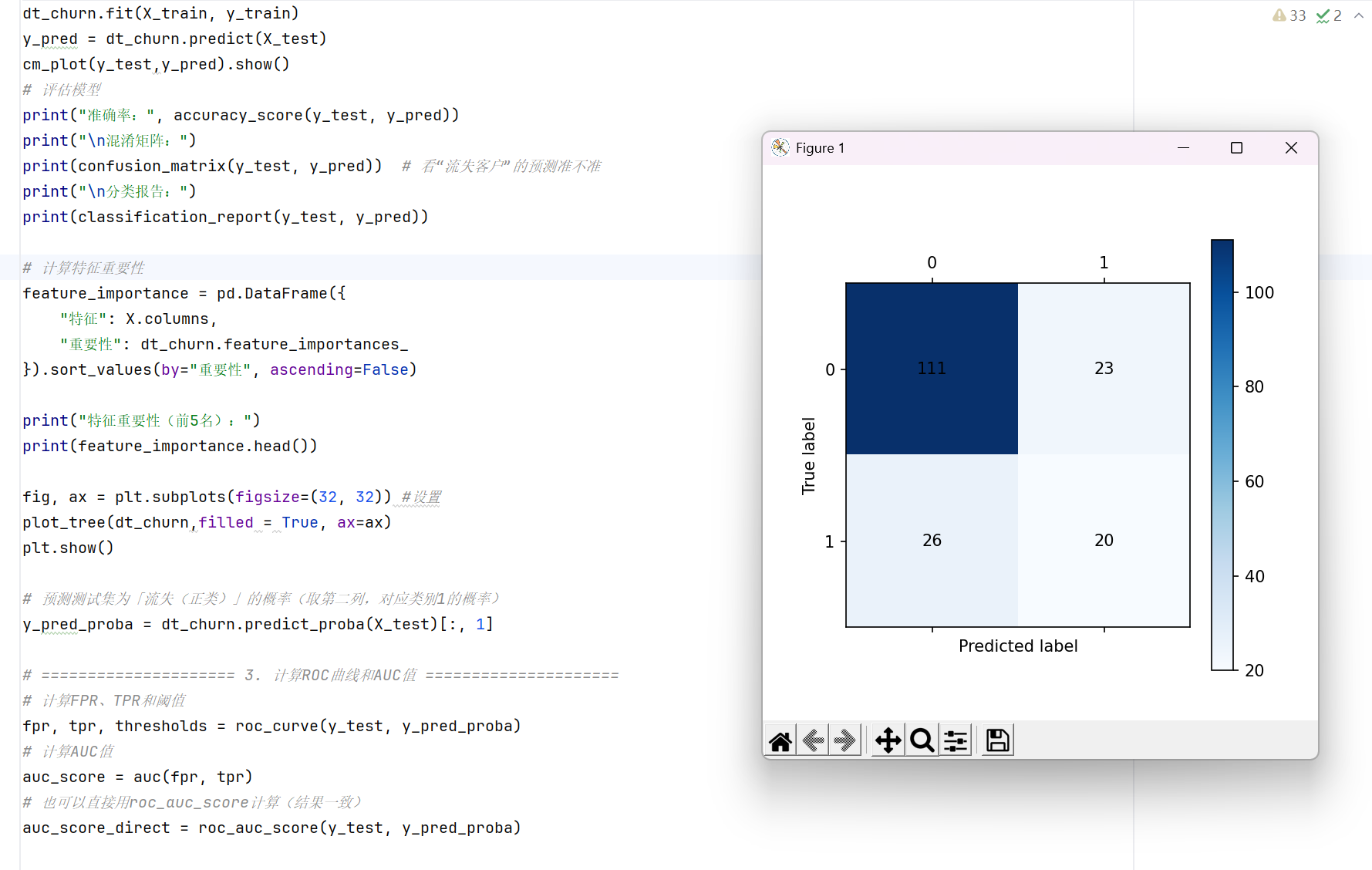

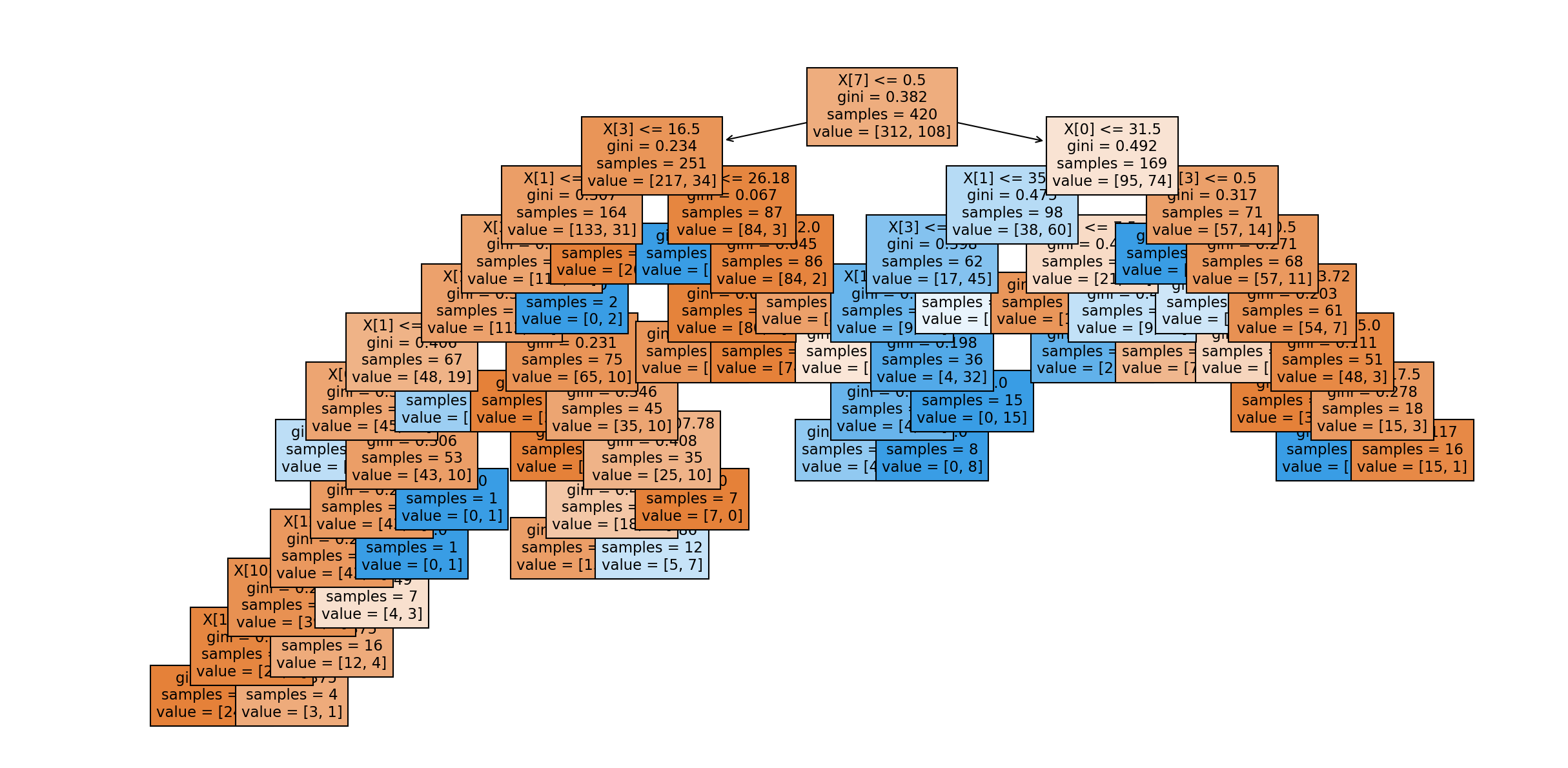
决策树之回归树模型

解决回归问题的决策树模型即为回归树（必须是二叉树）

决策树的回归树（Regression Tree）是用于预测连续型标签 （如客户月消费、房价）的树形模型，核心逻辑是通过递归划分特征空间，让每个叶节点输出一个代表该区域的数值（通常是该区域样本的均值）。

一、回归树的核心逻辑

与分类树（用 "纯度" 划分）不同，回归树用 **"误差最小化"** 作为划分标准，主流准则是：

均方误差（MSE）：MSE(D)=∣D∣1∑x∈D(y(x)−yˉD)2（yˉD是数据集D的标签均值）
平均绝对误差（MAE）：MAE(D)=∣D∣1∑x∈D∣y(x)−yˉD∣

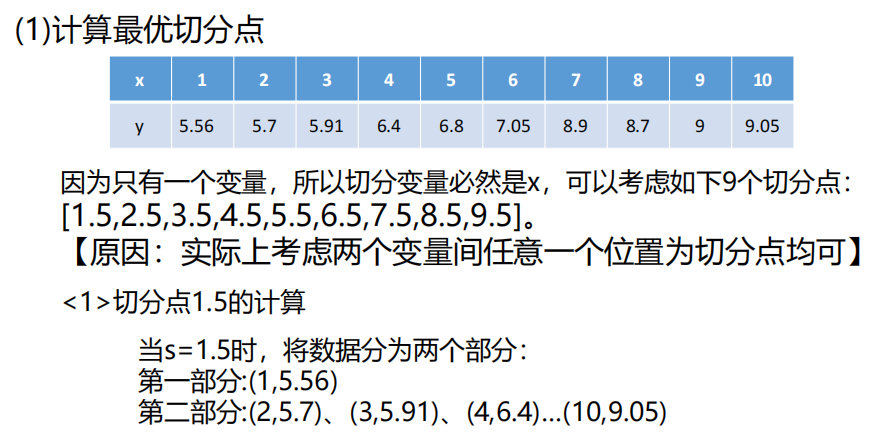
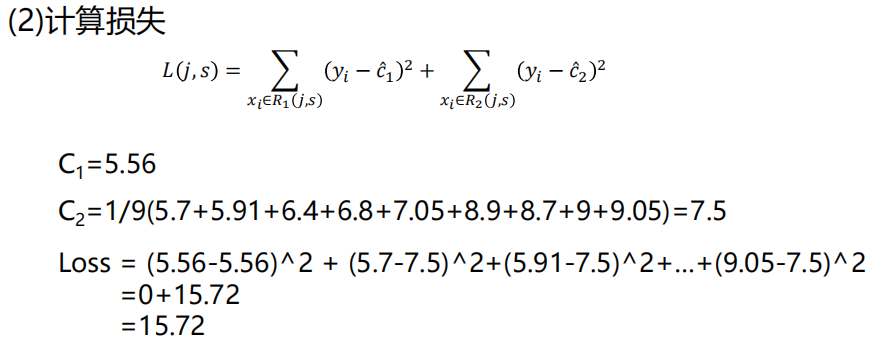
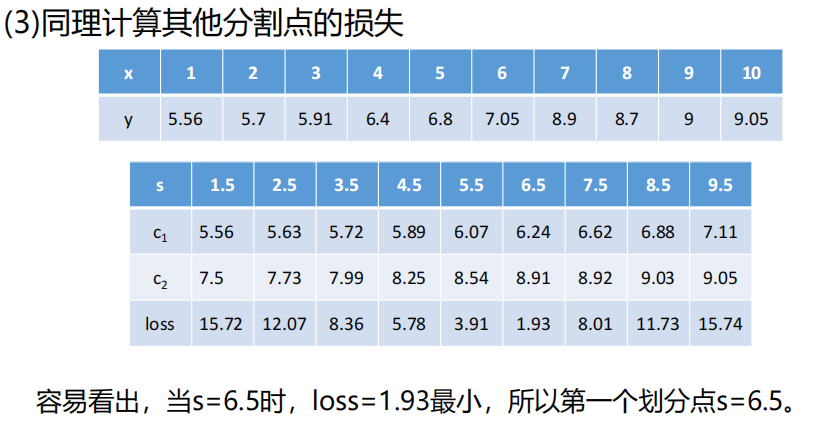
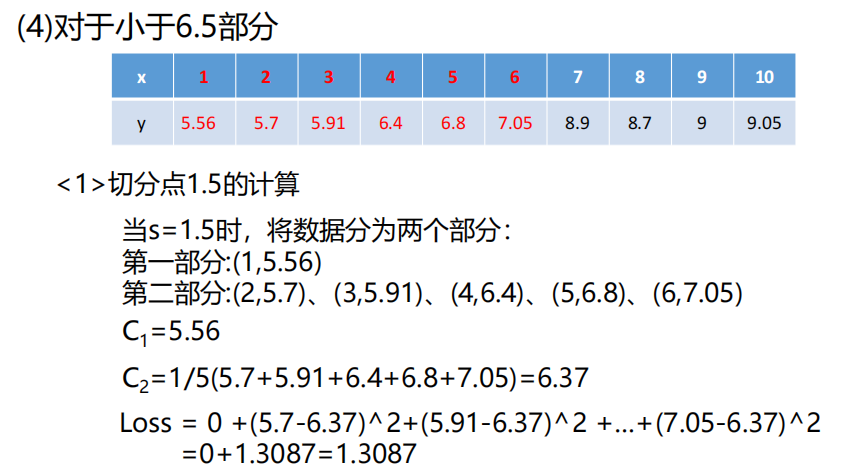
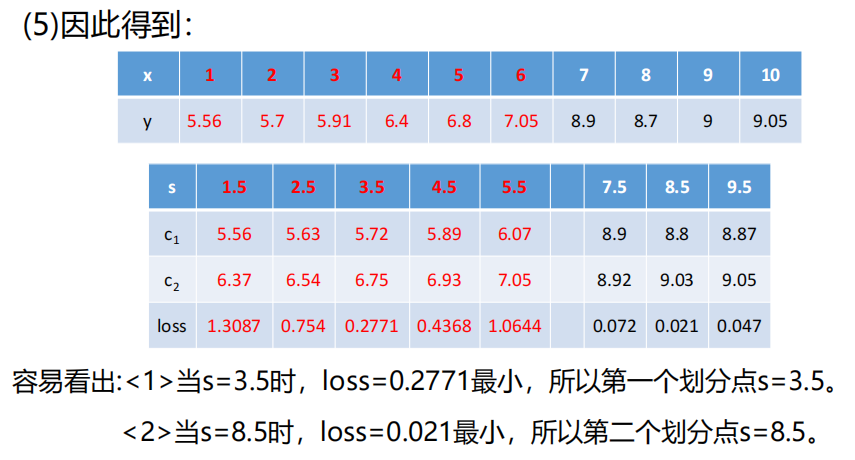
划分过程：

对每个特征A的每个可能阈值t，将数据拆分为D1（A≤t）和D2（A>t）；
计算拆分后的加权 MSE：MSEsplit=∣D∣∣D1∣MSE(D1)+∣D∣∣D2∣MSE(D2)；
选择 "加权 MSE 最小" 的特征 + 阈值作为当前节点的划分规则；
递归划分，直到满足停止条件（如树深度、叶节点样本数）；
叶节点输出该区域样本的标签均值。

二、回归树 vs 分类树的区别

维度	分类树	回归树
标签类型	离散型（类别）	连续型（数值）
划分准则	熵 / 基尼系数（纯度）	MSE/MAE（误差）
叶节点输出	类别（多数投票）	数值（区域均值）
评估指标	准确率、AUC	MSE、R²、MAE

AUC性能测量

在机器学习中，AUC（Area Under the ROC Curve） 是 ROC 曲线下的面积，是评估二分类模型性能的核心指标，尤其适合类别不平衡场景（如电信客户流失预测：流失客户少、未流失客户多）。

一、AUC 核心基础

1. 本质含义

AUC 衡量模型区分正类（如 "流失"）和负类（如 "未流失"） 的能力：

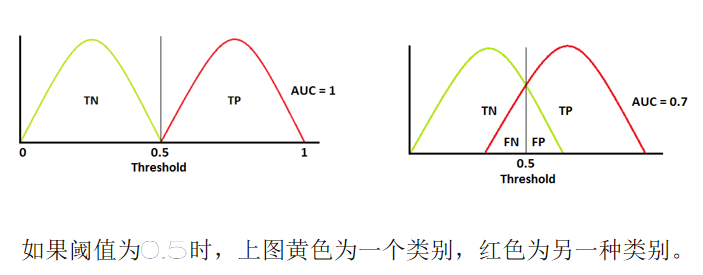
AUC = 1：模型完美区分正 / 负类（所有正类预测概率＞负类）；
0.8 ≤ AUC ＜ 1：模型区分能力优秀；
0.7 ≤ AUC ＜ 0.8：模型区分能力良好；
0.5 ≤ AUC ＜ 0.7：模型区分能力一般（仅比随机猜测好）；
AUC = 0.5：模型等同于随机猜测；
AUC ＜ 0.5：模型完全失效（反向预测可接近 1）。

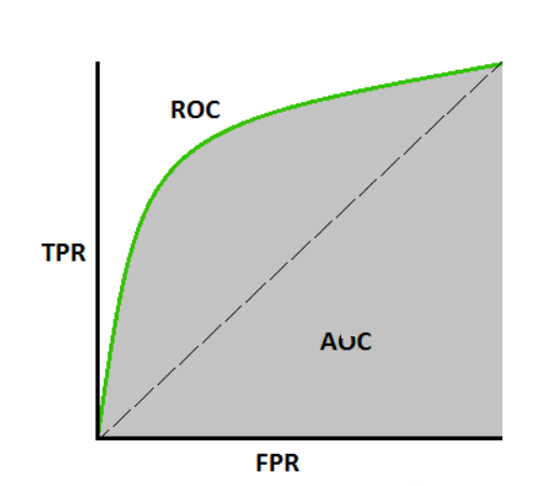
2. 与 ROC 的关系

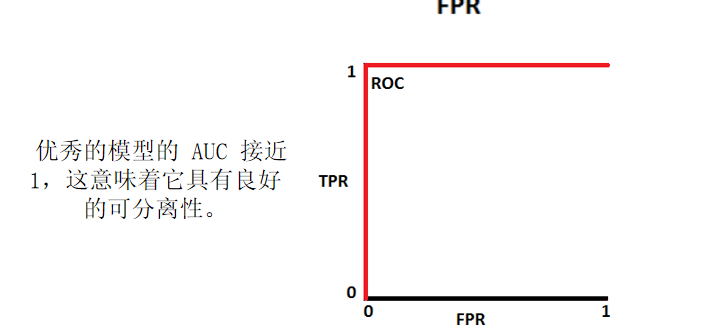
ROC 曲线以假正例率（FPR） 为横轴、真正例率（TPR） 为纵轴：

TPR（召回率）：实际正类中被正确预测为正类的比例 → TPR=TP+FNTP；
FPR：实际负类中被错误预测为正类的比例 → FPR=FP+TNFP；
AUC 是 ROC 曲线与坐标轴围成的面积，越接近 1 越好。

3. 适用场景

类别不平衡（如流失率 10%）：AUC 比 "准确率" 更可靠（准确率易被多数类主导）；
关注 "区分能力" 而非 "绝对预测准度"：如预测 "哪些客户更可能流失"（排序能力）。

二、AUC 计算前提

AUC仅适用于二分类模型，且需要模型输出「预测为正类的概率 / 得分」（而非直接的类别）：

分类树：用predict_proba()输出正类概率；
回归树：若强行用于二分类（如将连续标签二值化），需先将预测值映射为概率（或直接用预测值作为得分）。

python 复制代码

# 预测测试集为「流失（正类）」的概率（取第二列，对应类别1的概率）
y_pred_proba = dt_churn.predict_proba(X_test)[:, 1]

# ===================== 3. 计算ROC曲线和AUC值 =====================
# 计算FPR、TPR和阈值
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
# 计算AUC值
auc_score = auc(fpr, tpr)
# 也可以直接用roc_auc_score计算（结果一致）
auc_score_direct = roc_auc_score(y_test, y_pred_proba)

print(f"AUC值（auc函数）：{auc_score:.4f}")
print(f"AUC值（roc_auc_score函数）：{auc_score_direct:.4f}")

# ===================== 4. 绘制ROC曲线 =====================
plt.figure(figsize=(8, 6))
# 绘制ROC曲线
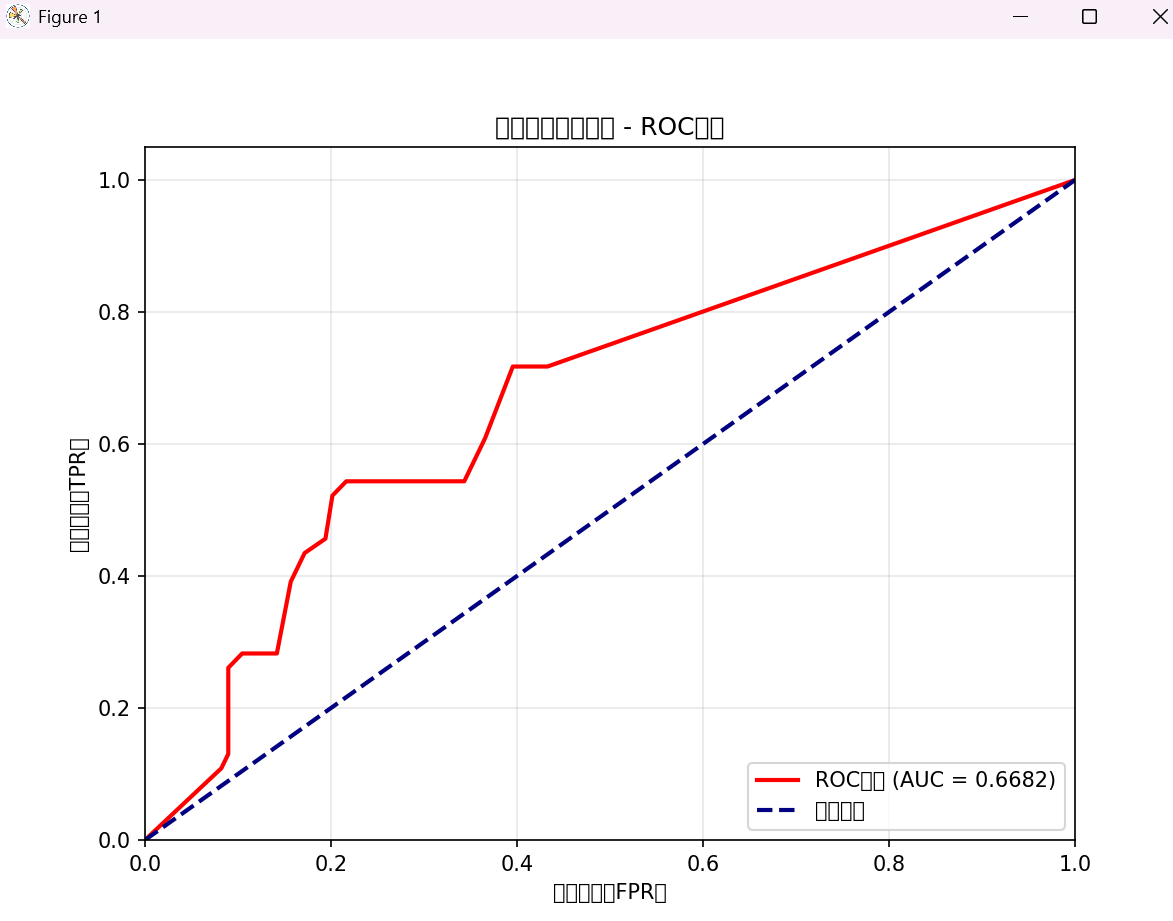
plt.plot(fpr, tpr, color='red', lw=2, label=f'ROC曲线 (AUC = {auc_score:.4f})')
# 绘制随机猜测的基准线（对角线）
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
# 图表美化
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正例率（FPR）')
plt.ylabel('真正例率（TPR）')
plt.title('电信客户流失预测 - ROC曲线')
plt.legend(loc="lower right")
plt.grid(alpha=0.3)
plt.show()