算法-栈与队列

一、栈和队列的用法

1.1 双端队列

通常使用到栈的时候可以使用ArrayDeque，实际上ArrayDeque是一个双端队列，既可以当栈使用又可以当队列使用。

import java.util.ArrayDeque;

// 默认初始容量为 16
ArrayDeque<Integer> deque = new ArrayDeque<>();

// 指定初始容量
ArrayDeque<String> dequeWithCapacity = new ArrayDeque<>(32);

1.1.1 双端操作

添加元素：

方法	作用	队列满时的行为
addFirst(e)	在头部插入元素	抛出 IllegalStateException
addLast(e)	在尾部插入元素	抛出 IllegalStateException
offerFirst(e)	在头部插入元素	返回 false（推荐使用）
offerLast(e)	在尾部插入元素	返回 false（推荐使用）

删除元素：

方法	作用	队列空时的行为
removeFirst()	移除并返回头部元素	抛出 NoSuchElementException
removeLast()	移除并返回尾部元素	抛出 NoSuchElementException
pollFirst()	移除并返回头部元素	返回 null（推荐使用）
pollLast()	移除并返回尾部元素	返回 null（推荐使用）

查看元素（不删除）：

方法	作用	队列空时的行为
getFirst()	返回头部元素	抛出 NoSuchElementException
getLast()	返回尾部元素	抛出 NoSuchElementException
peekFirst()	返回头部元素	返回 null（推荐使用）
peekLast()	返回尾部元素	返回 null（推荐使用）

1.1.2 替代 Stack 类（更高效的栈）

ArrayDeque<Integer> stack = new ArrayDeque<>();
stack.push(1);
stack.push(2);
int top = stack.pop(); // 返回 2

1.1.3 实现普通队列（FIFO）

ArrayDeque<String> queue = new ArrayDeque<>();
queue.offer("A");  // 尾部插入
queue.offer("B");
String head = queue.poll(); // 头部移除，返回 "A"

1.2 优先级队列

PriorityQueue 是一个基于优先级堆的无界队列，元素按照自然顺序或自定义顺序排序。

1.2.1 定义

// 默认最小堆（自然顺序）
PriorityQueue<Integer> minHeap = new PriorityQueue<>();

// 自定义比较器（如最大堆）
// 使用Lambda表达式
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
// 或使用内置比较器
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());


// 自定义对象排序
PriorityQueue<Task> pq = new PriorityQueue<>(
    Comparator.comparingInt(t -> t.priority)
);

1.2.2 操作

// 添加元素
pq.offer(5);  // 推荐使用，返回布尔值
pq.add(3);    // 队列满时抛出异常（但PriorityQueue无界）

// 获取队首元素
int head = pq.peek(); // 返回队首元素（不删除）

// 移除元素
int head = pq.poll(); // 移除并返回队首元素（队列空时返回null）
pq.remove(obj);       // 删除指定元素（需存在）

二、栈与队列

2.1 用栈实现队列

leetcode题目链接：232. 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 ------ 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

解法：

class MyQueue {
    Stack<Integer> inStack = new Stack<Integer>();
    Stack<Integer> outStack = new Stack<Integer>();
    public MyQueue() {
        inStack = new Stack<Integer>();
        outStack = new Stack<Integer>();
    }
    
    public void push(int x) {
        inStack.push(x);
    }
    
    public int pop() {
        if (outStack.isEmpty()) {
            while(!inStack.isEmpty()){
                outStack.push(inStack.pop());
            }
        }

        return outStack.pop();
    }
    
    public int peek() {
        if (outStack.isEmpty()) {
            while(!inStack.isEmpty()){
                outStack.push(inStack.pop());
            }
        }

        return outStack.peek();
        
    }
    
    public boolean empty() {
        return inStack.isEmpty() && outStack.isEmpty();
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

2.2 用队列实现栈

leetcode题目链接：225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的标准操作 ------ 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

解法：

class MyStack {
    // 主队列，始终保持queue1中按照新元素在最前面的顺序保存所有元素
    LinkedList<Integer> queue1 = new LinkedList<>();
    // 辅助队列
    LinkedList<Integer> queue2 = new LinkedList<>();

    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    public void push(int x) {
        // queue2负责接收最新的元素
        queue2.offer(x);
        // queue2接收完最新元素之后，把queue1中的元素全部按照顺序放入queue2
        while(!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        
        // 交换queue1与queue2，始终保持queue1中按照新元素在最前面的顺序保存所有元素
        LinkedList<Integer> temp = queue1;
        queue1 = queue2;
        queue2 = temp;
    }
    
    public int pop() {
        return queue1.poll();
    }
    
    public int top() {
        return queue1.peek();
    }
    
    public boolean empty() {
        return queue1.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

2.3 最小栈

leetcode题目链接：155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

解法：

/**
 * 使用两个栈，stack用于存储所有元素，minStack用于存储当前的最小值。
 */
class MinStack {
    private Deque<Integer> stack;
    private Deque<Integer> minStack;

    public MinStack() {
        stack = new ArrayDeque<>();
        minStack = new ArrayDeque<>();
    }

    public void push(int val) {
        stack.push(val);
        if (minStack.isEmpty() || val <= minStack.peek()) {
            minStack.push(val);
        }
    }

    public void pop() {
        int val = stack.pop();
        if (val == minStack.peek()) {
            minStack.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

2.4 有效的括号

leetcode题目链接：20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

**输入：**s = "()"

**输出：**true

示例 2：

**输入：**s = "()[]{}"

**输出：**true

示例 3：

**输入：**s = "(]"

**输出：**false

解法：

class Solution {
    public boolean isValid(String s) {
        if(s == null || s.length() == 0){
            return true;
        }

        char[] arr = s.toCharArray();
        Stack<Character> stack = new Stack<Character>();
        for(int i = 0; i < arr.length; i++){
            if(arr[i] == '(' || arr[i] == '[' || arr[i] == '{'){
                stack.push(arr[i]);
                continue;
            }

            if(stack.isEmpty()){
                return false;
            }
            Character top = stack.pop();
            
            if(arr[i] == ')' && top != '('){
                return false;
            }
            if(arr[i] == '}' && top != '{'){
                return false;
            }
            if(arr[i] == ']' && top != '['){
                return false;
            }
        }
        
        return stack.isEmpty();
    }
}

2.5 删除字符串中的所有相邻重复项

leetcode题目链接：1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 s 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

解法：

class Solution {
    public String removeDuplicates(String s) {
        if(s == null || s. length() == 0){
            return s;
        }
        
        char[] arr = s.toCharArray();
        // 先使用栈结构对元素进行去重
        ArrayDeque<Character> deque = new ArrayDeque();
        for(char c : arr){
            if(deque.isEmpty() || deque.peek() != c){
                deque.offerFirst(c);
            }else{
                deque.pollFirst();
            }
        }
        
        // 栈中的数据转化为字符串
        StringBuilder sb = new StringBuilder();
        while(!deque.isEmpty()){
            sb.append(deque.pollLast());
        }

        return sb.toString();
    }
}

2.6 逆波兰表达式求值

leetcode题目链接：150. 逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/' 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

• 1 <= tokens.length <= 104
• tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

解法：

class Solution {
    /**
     * 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中
     */
    public int evalRPN(String[] tokens) {
        ArrayDeque<Integer> stack = new ArrayDeque<Integer>();
        for(String token: tokens){
            if(token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/")){
                Integer a = stack.pop();
                Integer b = stack.pop();
                Integer result = 0;
                switch (token) {
                    case "+":
                        result = b + a;
                        break;
                    case "-":
                        result = b - a;
                        break;
                    case "*":
                        result = b * a;
                        break;
                    case "/":
                        result = b / a;
                        break;
                }
                stack.push(result);
            }else{
                stack.push(Integer.parseInt(token));
            }
        }

        return stack.pop();
    }
}

2.7 前K个高频元素

leetcode题目链接：347. 前K个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1：

**输入：**nums = [1,1,1,2,2,3], k = 2

输出：[1,2]

示例 2：

**输入：**nums = [1], k = 1

输出：[1]

示例 3：

**输入：**nums = [1,2,1,2,1,2,3,1,3,2], k = 2

输出：[1,2]

解法：

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 统计nums中元素出现的个数，放入map中。key是nums中的值，value指出现的次数
        Map<Integer, Integer> map = new HashMap<>();
        for(Integer num : nums){
            map.put(num, map.getOrDefault(num, 0)+1);
        }

        // 为了找到前k频繁的num，构建一个优先级队列，按照出现的次数从小到大排序
        PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<Map.Entry<Integer, Integer>>((a, b) -> a.getValue() - b.getValue());
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
            queue.offer(entry);
            if(queue.size() > k){
                queue.poll();
            }
        }

        // 从优先级队列中取值，塞入结果数组中
        int[] result = new int[k];
        for(int i = k-1; i >= 0; i--){
            if(!queue.isEmpty()){
                result[i] = queue.poll().getKey();
            }
        }

        return result;
    }
}

2.8 字符串解码

leetcode题目链接：394. 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

测试用例保证输出的长度不会超过 105。

示例 1：

输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

解法：

/**
 * 解码字符串，处理形如k[encoded_string]的嵌套编码结构
 */
class Solution {
    /**
     * 解码给定的编码字符串
     *
     * @param s 输入的编码字符串，格式符合题目要求
     * @return 解码后的字符串
     */
    public String decodeString(String s) {
        // 存储重复次数的栈（处理嵌套时保存外层数字）
        Stack<Integer> numStack = new Stack<>();
        // 存储字符串片段的栈（处理嵌套时保存外层字符串）
        Stack<String> strStack = new Stack<>();
        // 当前正在构建的结果字符串
        StringBuilder res = new StringBuilder();
        // 当前解析到的重复次数（用于处理多位数）
        int num = 0;

        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            // 1. 处理数字字符：逐位计算完整重复次数
            if (Character.isDigit(c)) {
                num = num * 10 + (c - '0'); // 处理连续数字（例如"123"转换为整数123）
            }
            // 2. 遇到左括号：压栈并重置状态，进入新嵌套层级
            else if (c == '[') {
                strStack.push(res.toString()); // 当前字符串暂存栈中（外层字符串）
                numStack.push(num);            // 当前数字暂存栈中（外层数字）
                res = new StringBuilder();     // 重置，开始处理内层字符串
                num = 0;                       // 重置数字计数器
            }
            // 3. 遇到右括号：弹栈并拼接字符串，完成当前层解码
            else if (c == ']') {
                int k = numStack.pop();        // 获取当前层重复次数
                String prevStr = strStack.pop();// 获取外层未完成的字符串
                // 将内层字符串重复k次，拼接在外层字符串后
                StringBuilder temp = new StringBuilder(prevStr);
                String current = res.toString();
                for (int j = 0; j < k; j++) {
                    temp.append(current);
                }
                res = new StringBuilder(temp.toString()); // 更新为拼接后的结果
            }
            // 4. 处理普通字符：直接追加到当前结果
            else {
                res.append(c);
            }
        }
        return res.toString();
    }
}

2.9 数组中的第K个最大元素

leetcode题目链接：215. 数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

解法：

class Solution {
    /**
     * 优先级队列，队列中的元素从小到大排序
     * 每进来一个元素就挤走当前k个元素中的最小值（也就是队列的头部元素）
     */
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> queue = new PriorityQueue<Integer>((a, b) -> a - b);
        for(int num : nums){
            queue.offer(num);
            if(!queue.isEmpty() && queue.size() > k){
                queue.poll();
            }
            
        }
        
        return queue.poll();
    }
}

2.10 数据流的中位数

leetcode题目链接：295. 数据流的中位数

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

• 例如 arr = [2,3,4] 的中位数是 3 。
• 例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

实现 MedianFinder 类:

• MedianFinder() 初始化 MedianFinder 对象。

• void addNum(int num) 将数据流中的整数 num 添加到数据结构中。

• double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

示例 1：

输入
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]

解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1);    // arr = [1]
medianFinder.addNum(2);    // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3);    // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0

解法：

import java.util.Collections;
import java.util.PriorityQueue;

/**
 * MedianFinder 类用于动态维护数据流的中位数。
 * 通过两个堆（最大堆和最小堆）实现高效的中位数计算。
 */
public class MedianFinder {
    // 最大堆存储较小的一半元素，堆顶为最大值
    private PriorityQueue<Integer> maxHeap;
    // 最小堆存储较大的一半元素，堆顶为最小值
    private PriorityQueue<Integer> minHeap;

    /**
     * 构造函数初始化两个堆：
     * - maxHeap 使用逆序比较器实现最大堆
     * - minHeap 默认是最小堆
     */
    public MedianFinder() {
        maxHeap = new PriorityQueue<>(Collections.reverseOrder());
        minHeap = new PriorityQueue<>();
    }

    /**
     * 向数据结构中添加一个数字，并动态调整堆的平衡
     * @param num 待添加的整数
     */
    public void addNum(int num) {
        // 1. 先将新元素加入最大堆（较小的一半）
        maxHeap.offer(num);
        // 2. 将最大堆的堆顶（当前较小一半的最大值）转移到最小堆（较大的一半）
        minHeap.offer(maxHeap.poll());
        
        // 3. 平衡堆的大小：
        // 如果最大堆元素数量少于最小堆，说明需要从最小堆"借"一个最小值回来
        // 保证 maxHeap 的大小始终 >= minHeap
        if (maxHeap.size() < minHeap.size()) {
            maxHeap.offer(minHeap.poll());
        }
    }

    /**
     * 计算当前数据流的中位数
     * @return 中位数（偶数个元素时为两堆顶的平均值，奇数时为maxHeap堆顶）
     */
    public double findMedian() {
        // 总元素数为奇数时，maxHeap 的堆顶即为中位数
        if (maxHeap.size() > minHeap.size()) {
            return maxHeap.peek();
        } 
        // 总元素数为偶数时，取两堆顶的平均值
        else {
            // 使用 0.5 替代 /2.0 避免浮点精度问题，同时保证结果为 double 类型
            return (maxHeap.peek() + minHeap.peek()) * 0.5;
        }
    }
}

三、单调栈

3.1 每日温度

leetcode题目链接：739. 每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:

输入: temperatures = [30,60,90]
输出: [1,1,0]

解法：

class Solution {
    /**
     * 经典的单调栈解法
     */
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        // 初始值为0
        int[] result = new int[n];
        // 单调栈，里面存储的是下标.使用双端队列模拟单调递减栈
        ArrayDeque<Integer> stack = new ArrayDeque<Integer>();
        
        for(int i = 0; i < n; i++){
            // 当栈不为空且当前温度高于栈顶日期的温度时，说明找到了栈顶日期的更高温度
            while(!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]){
                // 弹出栈顶日期索引
                Integer index = stack.pop();
                // 计算等待天数并存入结果数组
                result[index] = i - index;
            }

            // 将当前日期索引压入栈中，保持栈内温度递减的特性
            stack.push(i);
        }
        
        // 栈中剩余未处理的日期说明后续没有更高温度，结果数组默认值0无需处理
        return result;
    }
}

3.2 下一个更大元素I

leetcode题目链接：496. 下一个更大元素I

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x大的元素。

给你两个没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组ans作为答案，满足ans[i]是如上所述的 下一个更大元素 。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

解法：

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int[] result = new int[n];
        for(int i = 0; i < n; i++){
            result[i] = -1;
        }
        
        // 先将nums1中的元素放入map中，key为元素，value为nums1中元素对应的索引
        Map<Integer, Integer> map1 = new HashMap<>();
        for(int i = 0; i < nums1.length; i++){
            map1.put(nums1[i], i);
        }
        
        // 遍历nums2，使用单调栈存储nums2中的元素，栈中的元素是单调递减的
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        for(int i = 0; i < nums2.length; i++){
            while(!stack.isEmpty() && nums2[i] > stack.peek()){
                Integer num = stack.pop();
                if(map1.get(num) != null){
                    result[map1.get(num)] = nums2[i];
                } 
            }
            
            stack.push(nums2[i]);
        }
        
        return result;
    }
}

3.3 下一个更大元素II

leetcode题目链接：503. 下一个更大元素II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

解法：

class Solution {
    /**
     * 相比下一个更大元素I，循环了2遍数组，确保不仅找元素后面比当前元素大的元素，还会找元素前面比当前元素大的元素
     */
    public int[] nextGreaterElements(int[] nums) {
        // 初始化结果数组
        int n = nums.length;
        int[] res = new int[n];
        Arrays.fill(res, -1);
        
        // 单调栈，遍历2遍数组
        Deque<Integer> stack = new ArrayDeque<>();
        for (int i = 0; i < 2 * n; i++) {
            int idx = i % n;
            int num = nums[idx];
            while (!stack.isEmpty() && nums[stack.peek()] < num) {
                int top = stack.pop();
                res[top] = num;
            }
            
            stack.push(idx);
        }
        return res;
    }
}

3.4 接雨水

leetcode题目链接：42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

解法：

class Solution {
    // // 解法一：暴力解法，将问题拆分成计算每一根柱子的存水量，再将所有柱子的存水量相加，得到总共的存水量
    // // 一根柱子的存水量怎么计算：找到这根柱子左右两侧的最高柱子（形成的蓄水池会包含当前柱子），取较低者-当前柱子的高度=当前柱子的蓄水量
    // public int trap(int[] height) {
    //     int result = 0;
        
    //     // 第一根柱子和最后一根柱子，都不会形成蓄水
    //     for(int i = 1; i < height.length - 1; i++){
    //         int leftMax = 0;
    //         int rightMax = 0;

    //         // 寻找左侧的最高柱子
    //         for(int j = 0; j <= i; j++){
    //             leftMax = Math.max(leftMax, height[j]);
    //         }

    //         // 寻找右侧的最高柱子
    //         for(int k = i; k < height.length; k++){
    //             rightMax = Math.max(rightMax, height[k]);
    //         }

    //         //计算当前柱子的储水量
    //         result += Math.min(leftMax, rightMax) - height[i];

    //     }

    //     return result;
    // }



    // 解法二：在上述的暴力法中，对于每个柱子，我们都需要从两头重新遍历一遍求出左右两侧的最大高度，这里是有很多重复计算的，很明显最大高度是可以记忆化的。
    // 具体在这里可以用数组边递推边存储，也就是常说的动态规划，DP
    public int trap2(int[] height) {
        int len = height.length;
        if(len<=1){
            return 0;
        }

        // dp[i][0]表示 下标i左侧的柱子最大高度
        // dp[i][1]表示下标i右侧的柱子最大高度
        // 当前柱子的存水量= min(dp[i][0],dp[i][1])-height[i]
        int[][] dp = new int[len][2];
        
        //初始化
        dp[0][0] = height[0];
        dp[len-1][1] = height[len-1];
        for(int i=1; i<len; i++){
            dp[i][0] = Math.max(height[i], dp[i-1][0]);
        }
 
        for(int i= len-2; i>=0; i--){
            dp[i][1] = Math.max(height[i], dp[i+1][1]);
        }

        // 遍历每个柱子，累加当前柱子顶部可以储水的高度，
        // 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
        int res=0;
        for(int i=1;i<len;i++){
             res += Math.min(dp[i][0], dp[i][1]) - height[i];
        }
 
        return res;
    }

    /**
     * 解法三：单调栈
     */
    public int trap(int[] height) {
        int res = 0; // 存储最终结果，即总接水量
        Deque<Integer> stack = new ArrayDeque<>(); // 单调栈，保存柱子索引，对应高度递减

        // 遍历每个柱子
        for (int i = 0; i < height.length; i++) {
            // 当栈非空且当前柱子高度大于栈顶柱子高度时，说明可能形成凹槽
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int top = stack.pop(); // 弹出栈顶元素作为凹槽的底部
                if (stack.isEmpty()) {
                    break; // 若栈空，说明没有左边界，无法接水，跳过
                }
                int left = stack.peek(); // 新的栈顶元素作为左边界
                int distance = i - left - 1; // 计算左右边界的水平距离
                // 计算有效接水高度（左右边界较矮者 - 底部高度）
                int boundedHeight = Math.min(height[left], height[i]) - height[top];
                res += distance * boundedHeight; // 累加该层的接水量
            }
            stack.push(i); // 将当前柱子索引入栈，保持栈的递减性
        }
        return res; // 返回总接水量
    }

}

3.5 柱状图中的最大矩形

leetcode题目链接：84. 柱状图中的最大矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

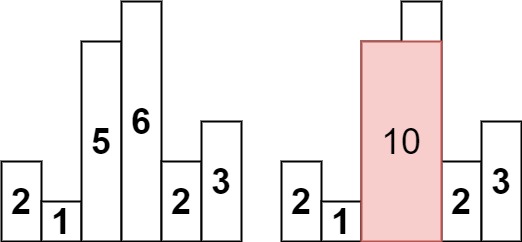
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

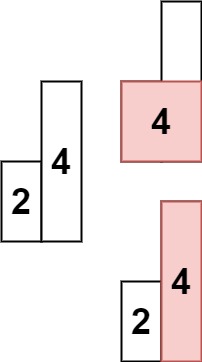
输入： heights = [2,4]
输出： 4

解法：

public class Solution {
    /**
     * 求解思路：遍历每个柱子，以每个柱子的高度为基准得到矩形的height，柱子左边第一个小于柱子高度的柱子作为左边界left，柱子右边第一个小于柱子高度的柱子作为有边界right，达到的矩形的面积=heigth*(right-left-1）
     * 方法一：动态规划，参考接雨水，使用动态规划分别计算每个柱子左侧第一个小于柱子高度的索引和右侧第一个小于柱子高度的索引，存入dp数组中。最后计算计算以每个柱子的height为基准得到矩形面积，取最大值。
     * 方法二：单调栈，因为涉及求解左/右侧第一个比他矮，可以使用单调栈的解法，具体解法如下
     */
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }
        Deque<Integer> stack = new ArrayDeque<>();
        int maxArea = 0;
        int n = heights.length;

        for (int i = 0; i < n; i++) {
            // 当前元素小于栈顶元素时，计算栈顶元素对应的最大面积
            while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
                int currentIndex = stack.pop();
                int height = heights[currentIndex];
                // 左边界是栈顶元素，若栈为空则为-1
                int left = stack.isEmpty() ? -1 : stack.peek();
                int width = i - left - 1;
                maxArea = Math.max(maxArea, height * width);
            }
            stack.push(i);
        }

        // 处理栈中剩余的元素，此时右边界为数组末尾
        while (!stack.isEmpty()) {
            int currentIndex = stack.pop();
            int height = heights[currentIndex];
            int left = stack.isEmpty() ? -1 : stack.peek();
            int width = n - left - 1;
            maxArea = Math.max(maxArea, height * width);
        }

        return maxArea;
    }
}