【剑斩OFFER】算法的暴力美学——翻转对

一、题目描述

二、算法原理

思路：归并排序（降序） + 双指针

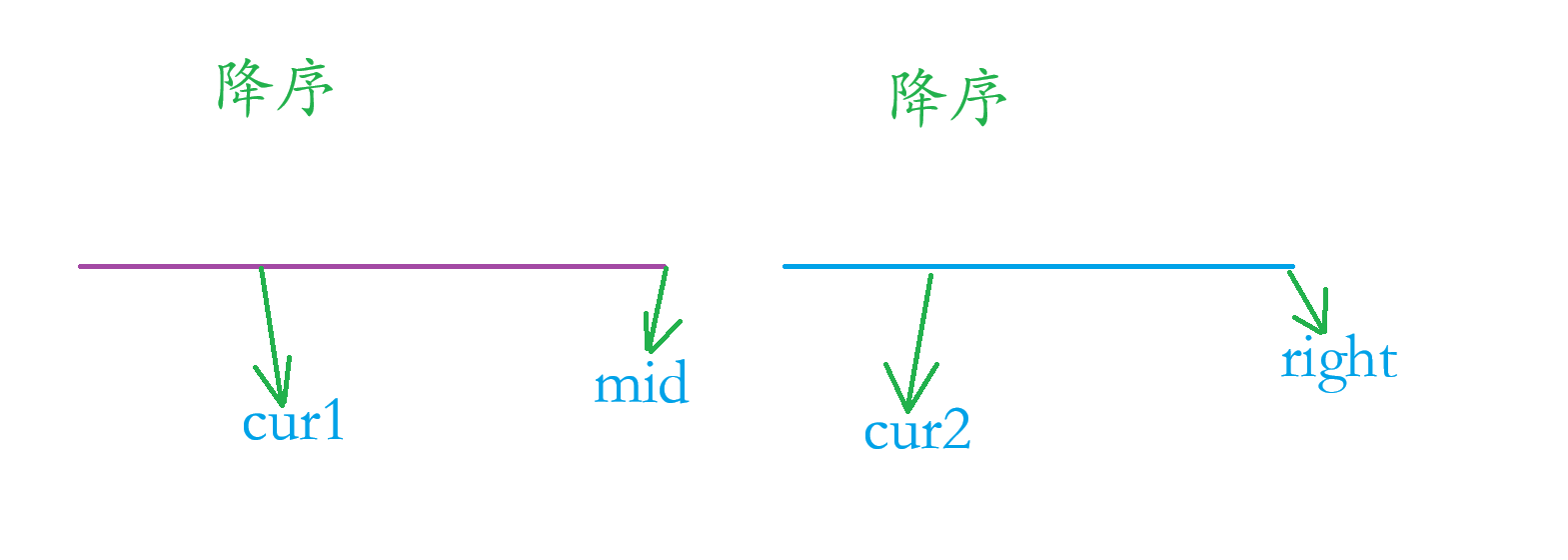
如果：nums $cur1$ <= 2 * nums $cur2$ ，那么证明我们还没有找到符合题目要求的 nums $cur$ ，所以：cur2 ++

如果：nums $cur1$ > 2 * nums $cur2$ ，符合题目要求，因为 nums $cur1$ > 2 * nums $cur2$ 又因为数组都是降序的，所以【 cur2，right 】这个区间的数字都符合题目要求。统计完符合题目要求的数字之后，那么 cur1++ 看看后面数字是否有数字大于2倍的nums $cur2$ ，那我们的 cur2 还要从头开始判断 nums $cur1$ <= 2 * nums $cur2$ 吗？答案是：不用，因为 cur1 没有 ++ 之前就已经没有符合题目要求了：nums $cur1$ <= 2 * nums $cur2$ （cur2：【mid + 1，cur2 - 1】），因为数组是降序的，cur1++ 之后更加不会符合题目要了；所以 cur2 不用返回数组的开头重新判断一遍，这样会增加时间复杂度的。

注意：上面的内容不能在合并数组的时候进行，在合并之前进行，因为在合并的时候进行会导致合并数组和找翻转对的过程冲突；所以我们要在合并数组之前进行，此时这两个数组都是有序的。

三、代码实现

cpp 复制代码

//降序找翻转对
class Solution {
    int count;
public:
    int reversePairs(vector<int>& nums) {
        count = 0;
        vector<int> tmp;
        tmp.resize(nums.size());
        Quicksort(0,nums.size() - 1,nums,tmp);
        return count;
    }

    void Quicksort(int l,int r,vector<int>& nums,vector<int>& tmp)
    {
        if(l >= r) return;
        
        int keyi = (l + r) >> 1;
        Quicksort(l,keyi,nums,tmp);//左边：【 l , keyi 】
        Quicksort(keyi + 1,r,nums,tmp);//右边：【keyi + 1,r 】

        int begin1 = l,end1 = keyi;//左边数组
        int begin2 = keyi + 1,end2 = r;//右边数组
        int index = l;//遍历起始点

        int begin3 = begin1,end3 = end1;
        int begin4 = begin2,end4 = end2;
        while(begin3 <= end3 && begin4 <= end4)//提前保存翻转对
        {
            long long tmp_i = 2 * (long long)nums[begin4];//防止数据丢失
            while(begin4 <= end4 && tmp_i >= nums[begin3])
            {
                begin4++;
                tmp_i = 2 * (long long)nums[begin4];
            }
            if(begin4 > end4) break;
            count += end4 - begin4 + 1;
            begin3++;
        }

        while(begin1 <= end1 && begin2 <= end2)//比较遍历
        {
            if(nums[begin1] > nums[begin2])
            {
                tmp[index++] = nums[begin1++];
            }
            else
            {
                tmp[index++] = nums[begin2++];
            }
        }

        while(begin1 <= end1) tmp[index++] = nums[begin1++];//把左边剩余的数字放到 tmp
        while(begin2 <= end2) tmp[index++] = nums[begin2++];//把右边剩余的数字放到 tmp
        
        for(int i = l;i < index;i++) nums[i] = tmp[i];//把 tmp 里面的数字放回到原数组 nums
    }
};

cpp 复制代码

//升序找翻转对
class Solution {
    int count;
public:
    int reversePairs(vector<int>& nums) {
        count = 0;
        vector<int> tmp;
        tmp.resize(nums.size());
        Quicksort(0,nums.size() - 1,nums,tmp);
        return count;
    }

    void Quicksort(int l,int r,vector<int>& nums,vector<int>& tmp)
    {
        if(l >= r) return;
        
        int keyi = (l + r) >> 1;
        Quicksort(l,keyi,nums,tmp);//左边：【 l , keyi 】
        Quicksort(keyi + 1,r,nums,tmp);//右边：【keyi + 1,r 】

        int begin1 = l,end1 = keyi;//左边数组
        int begin2 = keyi + 1,end2 = r;//右边数组
        int index = l;//遍历起始点

        int begin3 = begin1,end3 = end1;
        int begin4 = begin2,end4 = end2;
        while(begin3 <= end3 && begin4 <= end4)//提前保存翻转对
        {
            while(begin3 <= end3 && nums[begin3]/2.0 <= nums[begin4])//防止 5 / 2 = 2 == 2 ，所以不能/2 ，而是/2.0；5/2.0 = 2.5 > 2  
            {
                begin3++;
            }
            if(begin3 > end3) break;
            count += end3 - begin3 + 1;
            begin4++;
        }

        while(begin1 <= end1 && begin2 <= end2)//比较遍历，升序
        {
            if(nums[begin1] > nums[begin2])
            {
                tmp[index++] = nums[begin2++];
            }
            else
            {
                tmp[index++] = nums[begin1++];
            }
        }

        while(begin1 <= end1) tmp[index++] = nums[begin1++];//把左边剩余的数字放到 tmp
        while(begin2 <= end2) tmp[index++] = nums[begin2++];//把右边剩余的数字放到 tmp
        
        for(int i = l;i < index;i++) nums[i] = tmp[i];//把 tmp 里面的数字放回到原数组 nums
    }
};