机器学习--决策树

一、决策树

概念：决策树通过对训练样本的学习，并建立分类规则，然后依据分类规则，对新样本数据进行分类预测，属于有监督学习。

核心:所有数据从根节点一步一步落到叶子节点。

根节点：第一个节点

非叶子节点：中间节点

叶子节点：最终结果节点

例如

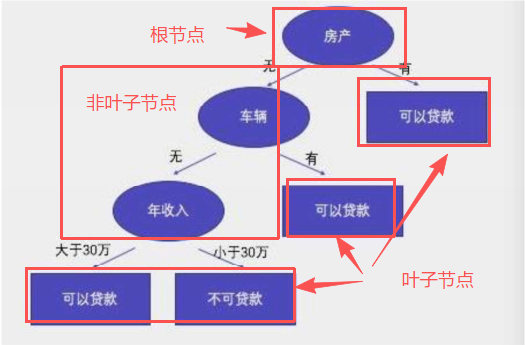
需要考虑的问题

1、哪个节点作为根节点？哪些节点作为中间节点？哪些节点作为叶子节点？

2、节点怎么分裂？

3、节点分裂标准的依据？

这个时候就要使用决策树的分类标准

1、决策树分类标准

1）ID3算法

衡量标准：

熵值:表示随机变量不确定性的度量，或者说是物体内部的混乱程度。

熵值计算公式：

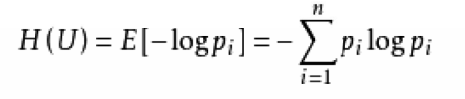
2）C4.5

衡量标准：信息增益率

3）CART

衡量标准：基尼系数

2、决策树剪枝

1）为什么要剪枝？

防止过拟合

2）如何剪枝？

预剪枝和后剪枝

3）预剪枝策略：

1、限制树的深度；

2、限制叶子节点的个数以及叶子节点的样本数；

3、基尼系数

3、结合实例理解

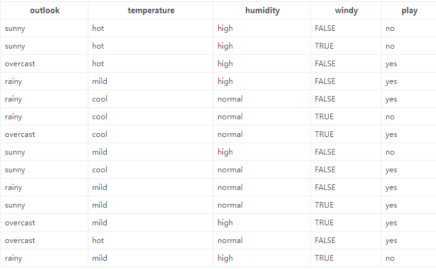
一、ID3算法：

熵：熵值越小，该节点越"纯"。

第一遍遍历：

1）标签（结果是否外出打球）的熵（类别熵）：

14天中，9天打球，5天不打球，熵为：

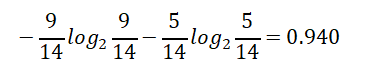
计算 对数的P ython程序 ：

import math

result = -9/14*math.log(9/14, 2) - 5/14*math.log(5/14, 2)

2）基于天气的划分

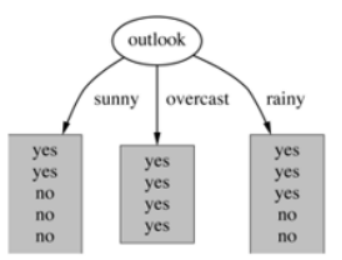
属性熵：

晴天【5天】的熵：

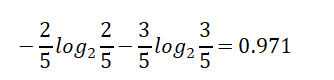
Overcast（阴天）【4天】的熵：

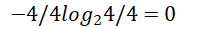
雨天【5天】的熵：

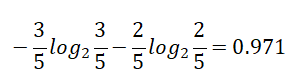
那么，天气对应标签结果的熵为：

熵值计算：

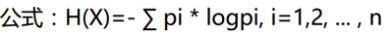
5/14*0.971+4/14*0+5/14*0.971=0.693

则 信息增益为： 0.940-0.693 =0.247

在决策树算法中，信息增益（information gain）是特征选择的一个重要指标。它描述的是一个特征能够为整个系统带来多少信息量（熵），用于度量信息不确定性减少的程度。

如果一个特征能够为系统带来最大的信息量，则该特征最重要，将会被选作划分数据集的特征。

3）基于温度的划分

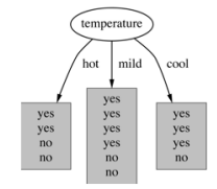
Hot【4天】的熵：

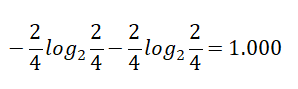
Mild【6天】的熵：

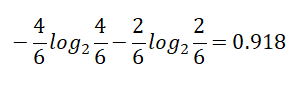
Cool【4天】的熵：

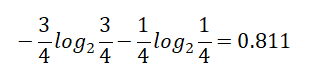
熵值计算：4/14*1+6/14*0.918+4/14*0.811=0.911

信息增益为：0.940 -- 0.911 = 0.029

4）基于湿度的划分

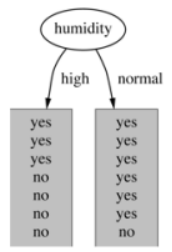
High【7天】的熵：

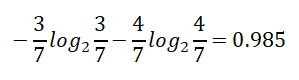
Normal【7天】的熵：

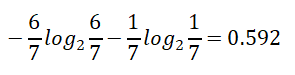
熵值计算：7/14*0.985+7/14*0.592=0.789

信息增益：0.940 -- 0.789 =0.151

5）基于有风的划分

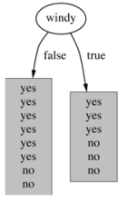
False【8天】的熵值：

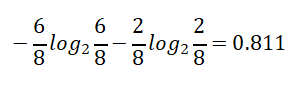
True【6天】的熵值：

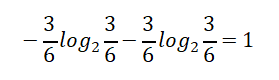
熵值计算：8/14*0.811 + 6/14*1 = 0.892

信息增益：0.940 - 0.892 = 0.048

综上：信息增益的大小：

天气：0.247

温度：0.029

湿度：0.151

有风：0.048

显然，信息增益最大的是： 天气 > 湿度 > 有风 > 温度

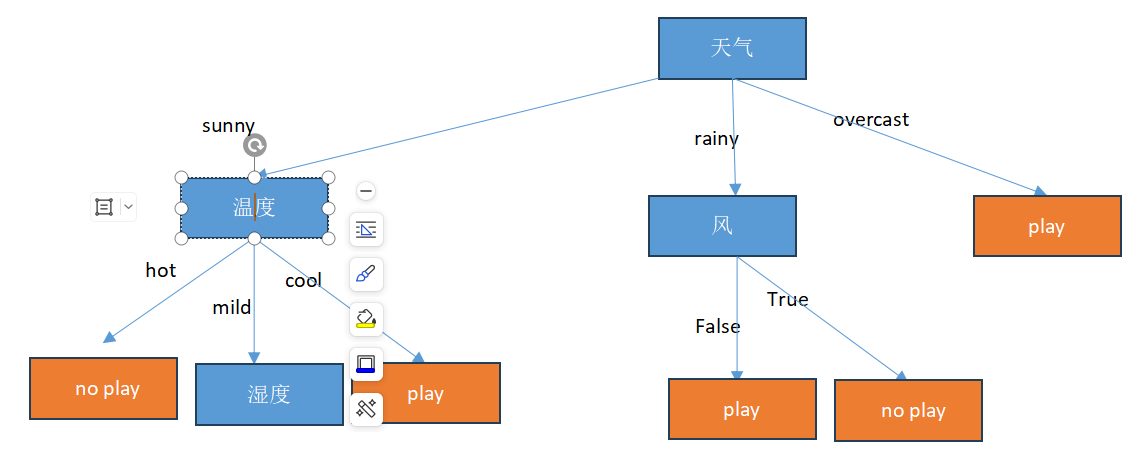
二 、 C4.5算法(解决稀疏向量的问题，例如编号)

C4.5算法是一种决策树生成算法，它使用信息增益比（gain ratio）来选择最优分裂属性，具体步骤如下：

1、计算所有样本的类别熵（H）。

2、对于每一个属性，计算该属性的熵【也为自身熵】（Hi）。

3、对于每一个属性，计算该属性对于分类所能够带来的信息增益（Gi = H - Hi）。

4、计算每个属性的信息增益比（gain ratio = Gi / Hi），即信息增益与类别自身熵的比值。

选择具有最大信息增益比的属性作为分裂属性。

第一遍计算： 【找 首要节点】

1.天气的信息增益为：

0.247，

天气的自身熵值：

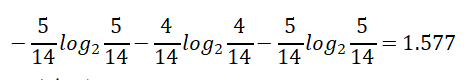
5天晴天、4天多云、5天有雨。

信息增益率：0.247/1.577 = 0.1566

2.温度的自身熵值：

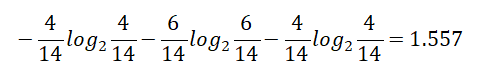
信息增益率：0.029/1.557 = 0.0186

3.湿度的自身熵值：

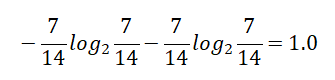
信息增益率：0.151/1.0 = 0.151

4.有风的自身熵值：

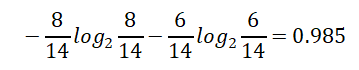
信息增益率：0.048/0.985 = 0.049

信息增益率排序：天气（0.1566）湿度（0.151）有风（0.049） 温度（0.0186）

天气 >湿度>有风>温度

三、CART决策树

用Gini指数最小化准则来进行特征选择。

基于基尼（GINI）指数

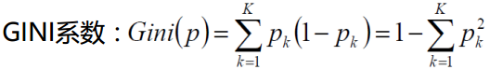
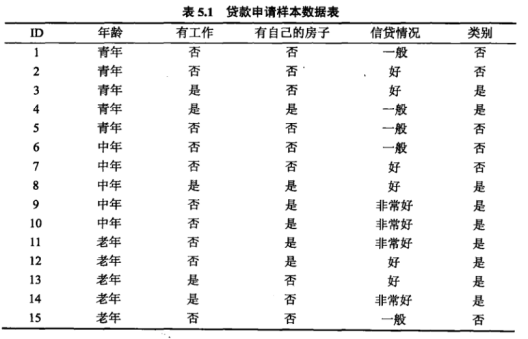
例：

特征A1（年龄）的基尼系数：

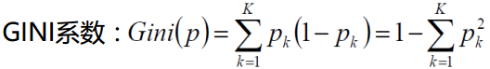
青年(5人，2人贷款)的基尼系数：

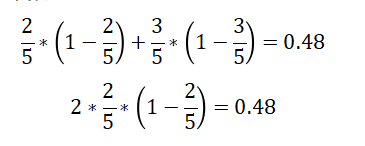
如果是类别是二分类，则 基尼系数：

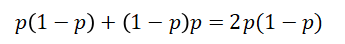
非青年（10人，7人贷款）的基尼系数：

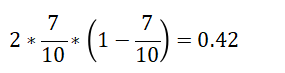
在A1=1（青年）条件下，D的基尼指数：

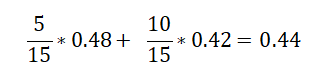
总公式：

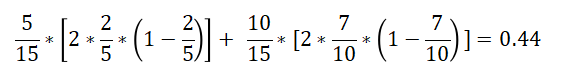
在A1=2（中年）条件下，D的基尼指数：

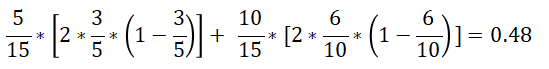
在A1=3条件下，D的基尼：

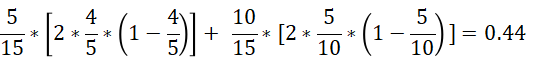
4、sklearn库中决策树参数问题（分类）

class sklearn.tree.DecisionTreeClassifier (criterion='gini' , splitter='best' , max_depth=None , min_samples_split=2 , min_samples_leaf=1 , min_weight_fraction_leaf=0.0 , max_features=None , random_state=None , max_leaf_nodes=None , min_impurity_decrease=0.0 , min_impurity_split=None , class_weight=None , presort=False)

树模型参数:

• 1.criterion :gini or entropy 【采用 基尼系数还是熵值衡量 ,默认 基尼系数 】
• 2.splitter: best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）【默认 best ， 无需更改 】
• 3.max_features: （表示寻找最优分裂时需要考虑的特征数量，默认为None，表示考虑所有特征。），log2，sqrt，N 特征小于50的时候一般使用所有的 【默认 取所有特征，无需更改 】
• 4.max_depth: **表示树的最大深度，**数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下。如果没有设置，那么将会把节点完全展开，直到所有的叶子节点都是纯的，或者达到最小叶子节点的个数阈值设置。

5.min_samples_split ： （表示分裂一个内部节点需要的最小样本数，默认为2），如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分，如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。【控制内部 节点分裂的情况 ；假设<10， 那么分裂的数量小于 10就不会再次 分裂了 ， 默认2个 】

5、电信客户流失数据案例

通过网盘分享的文件：电信客户流失数据.xlsx

链接: https://pan.baidu.com/s/19F-i3EHXrUvaCoxu54lJ1A 提取码: ym8t

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pylab import matplotlib
matplotlib.rcParams['font.sans-serif']=['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus']=False
# 可视化混淆矩阵
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix
    import matplotlib.pyplot as plt

    cm = confusion_matrix(y, yp)
    plt.matshow(cm, cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(y, x), horizontalalignment='center',
                         verticalalignment='center')
            plt.ylabel('True label')
            plt.xlabel('Predicted label')
    return plt


# 导入数据
datas = pd.read_excel("电信客户流失数据.xlsx")
# 将变量与结果划分开
x = datas.iloc[:, :-1]  # 1、datas.年龄    datas[年龄]   datas.iloc[ : , :-1]
y = datas.iloc[:, -1]  #

# 划分数据集
"""

导入模块对数据进行划分；
"""
from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test =train_test_split(x,y, test_size=0.2, random_state=50)

'''交叉验证'''
from sklearn import tree
from sklearn.model_selection import cross_val_score
scores=[]
max=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
for i in max:
    lr=tree.DecisionTreeClassifier(criterion='gini', max_depth=i, random_state=50)
    score=cross_val_score(lr,x_train,y_train,cv=8,scoring='recall')
    score_mean=sum(score)/len(score)
    scores.append(score_mean)
    print(score_mean)
best=max[np.argmax(scores)]
# 定义决策树
from sklearn import tree

dtr = tree.DecisionTreeClassifier(criterion='gini', max_depth=5, random_state=50)
dtr.fit(x_train, y_train)

"""
训练集混淆矩阵
"""
# 训练集预测值
train_predicted = dtr.predict(x_train)

from sklearn import metrics

# 绘制混淆矩阵
print(metrics.classification_report(y_train, train_predicted))
# 可视化混淆矩阵
cm_plot(y_train, train_predicted).show()

"""
测试集混淆矩阵
"""
# 测试集预测值
test_predicted = dtr.predict(x_test)  # 直接得到预测的结果

# 绘制混淆矩阵
print(metrics.classification_report(y_test, test_predicted))
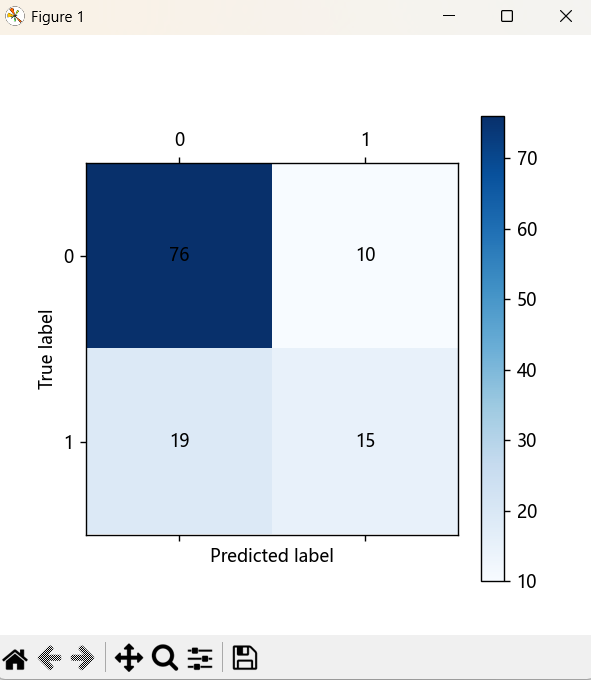
# 可视化混淆矩阵
cm_plot(y_test, test_predicted).show()
# 对决策树测试集进行评分
dtr.score(x_test, y_test)


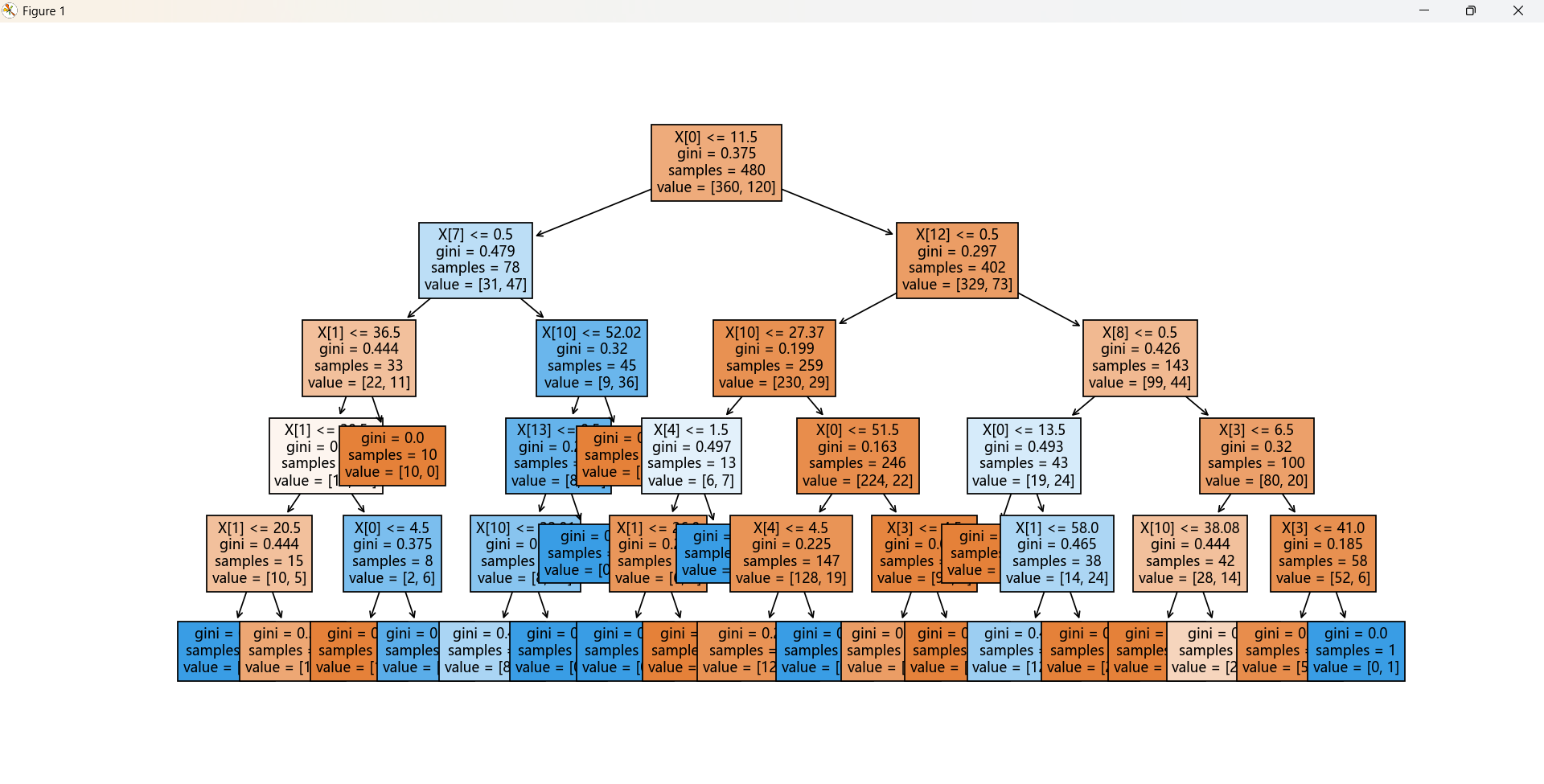
'''绘制决策树'''
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
fig,ax=plt.subplots(figsize=(30,30))
plot_tree(dtr,filled=True,ax=ax)
plt.show()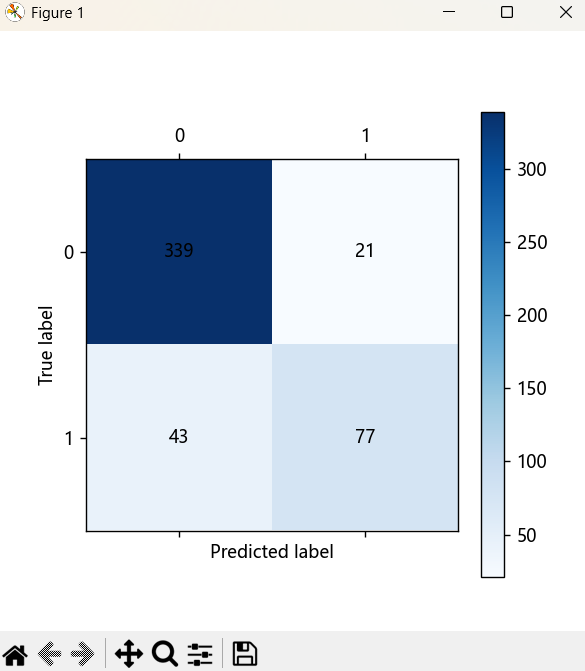

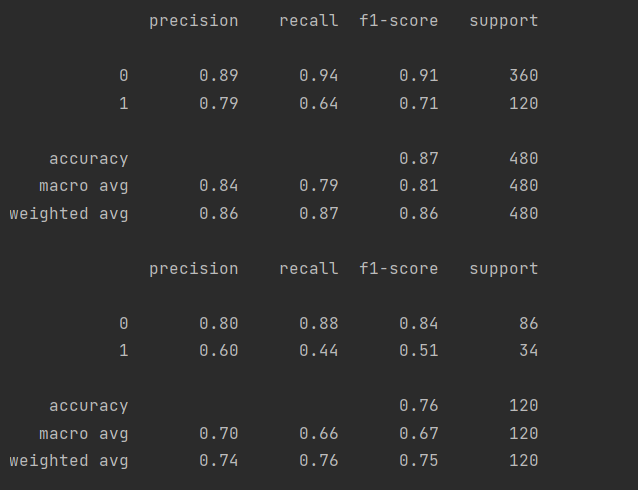
6、性能评判AUC

在机器学习中，性能测量是一项基本任务。因此，当涉及到分类问题时，我们可以依靠AUC - ROC曲线。当我们需要检查或可视化多类分类问题的性能时，我们使用AUC（曲线下面积）ROC（接收器工作特性）曲线。它是检查任何分类模型性能的最重要评估指标之一。

AUC - ROC 曲线是各种阈值设置下分类问题的性能度量。

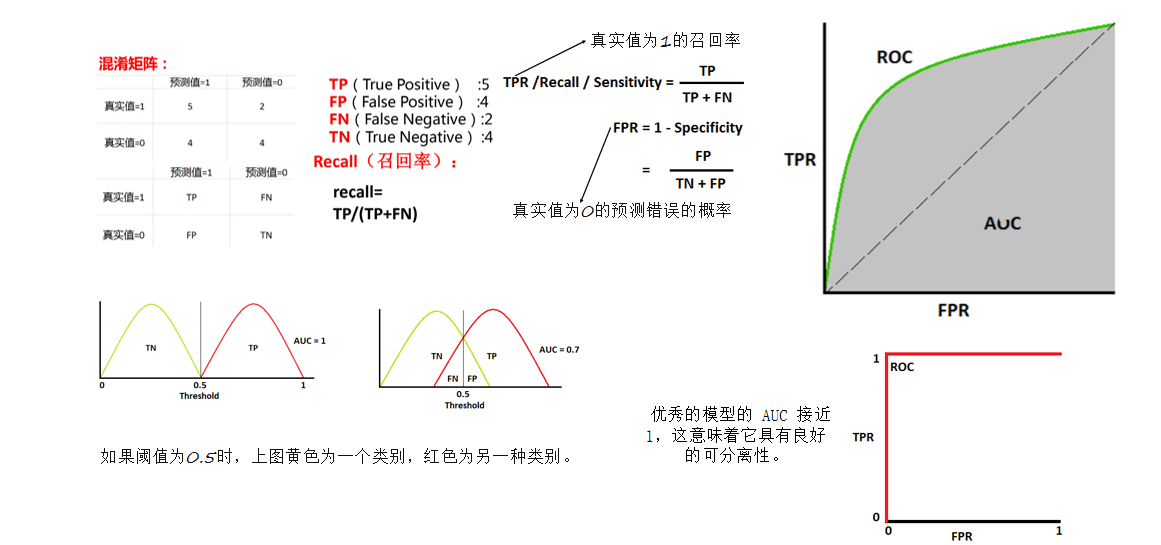
1）AUC的含义

AUC是衡量学习器优劣的一种性能指标。从定义可知，AUC可通过对ROC曲线下各部分的面积求和而得。AUC越大，说明模型对正负样本的区分能力越强，模型的性能也就越好。

2）AUC的优点

AUC考虑了分类器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器作出合理的评价。它不受样本不平衡问题的影响，因此是一个相对稳健的评价指标。

'''AUC值的计算'''
y_pred_proba = dtr.predict_proba(x_test)
a = y_pred_proba[:, 1]
auc_result = metrics.roc_auc_score(y_test, a)

'''绘制AUC-ROC曲线'''
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve#得到不同阈值的roc

# 计算ROC曲线的点
fpr, tpr, thresholds = roc_curve(y_test, a)#用来计算不同阈值下的fpr和tpr，

# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='r', lw=2, label='ROC curve(area=%0.2f)'% auc_result)
plt.plot([0, 1], [0, 1], color='b', lw=2, linestyle='--')#函数来绘制一条从点 (0,0) 到点 (1,1) 的线段。
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.1])
plt.xlabel('假正率')
# plt.xlabel('False Positive Rate')
plt.ylabel('真正率')
# plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend()
plt.show()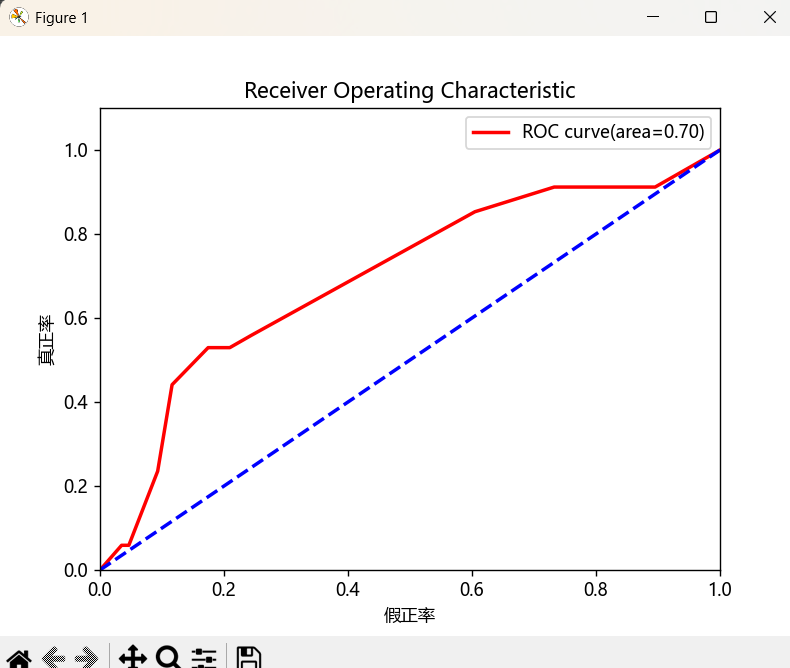

注：这里我用的标签有中文，这是因为我在前面的案例中使用了下面代码

from pylab import matplotlib
matplotlib.rcParams['font.sans-serif']=['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus']=False

7、决策树之回归树

何为回归树？
解决回归问题的决策树模型即为回归树。
特点：
必须是二叉树
1）决策数之回归树模型

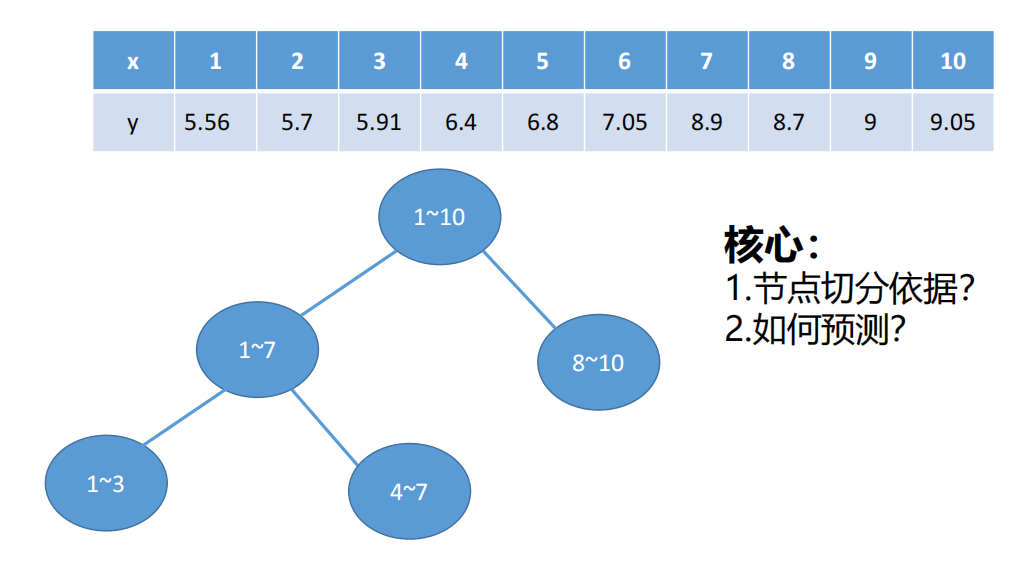
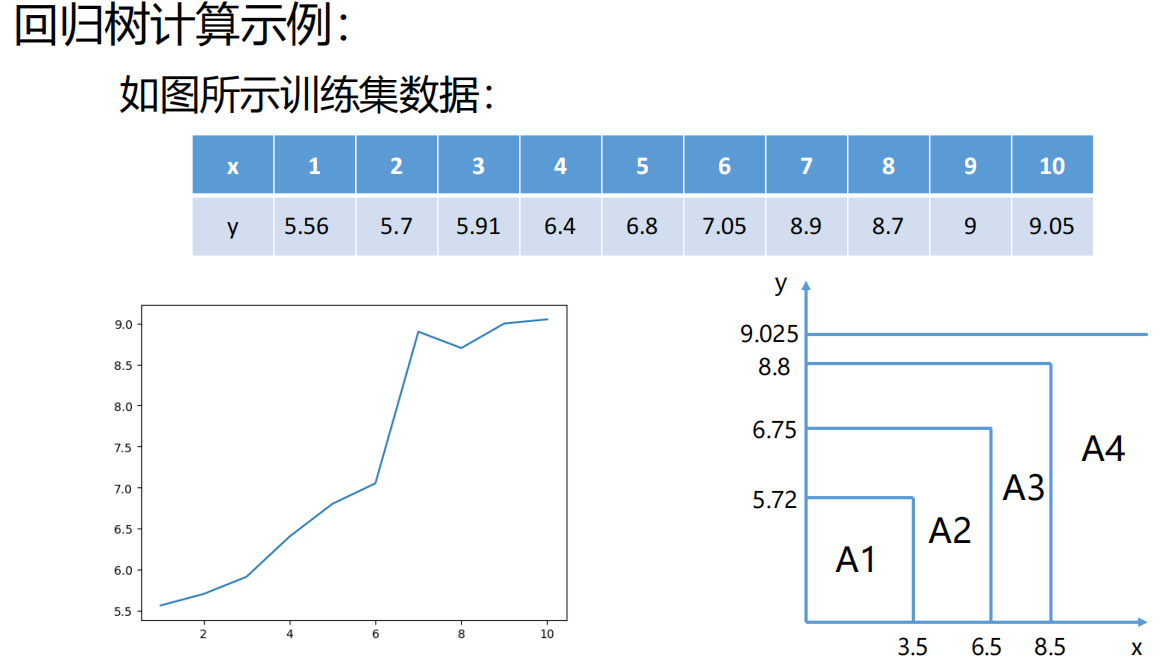
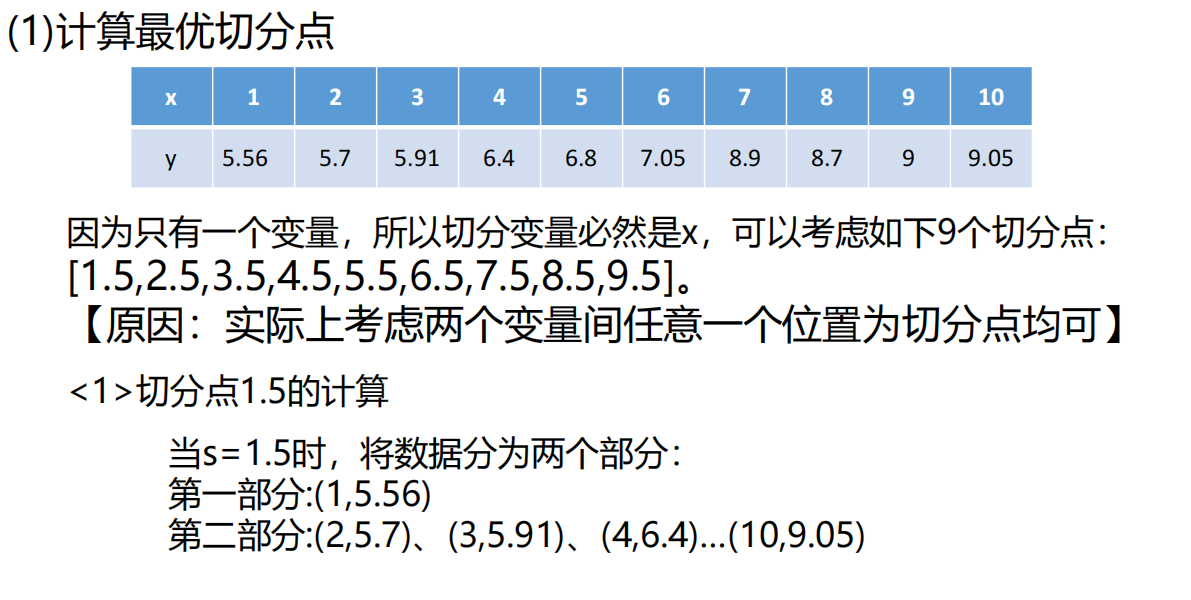
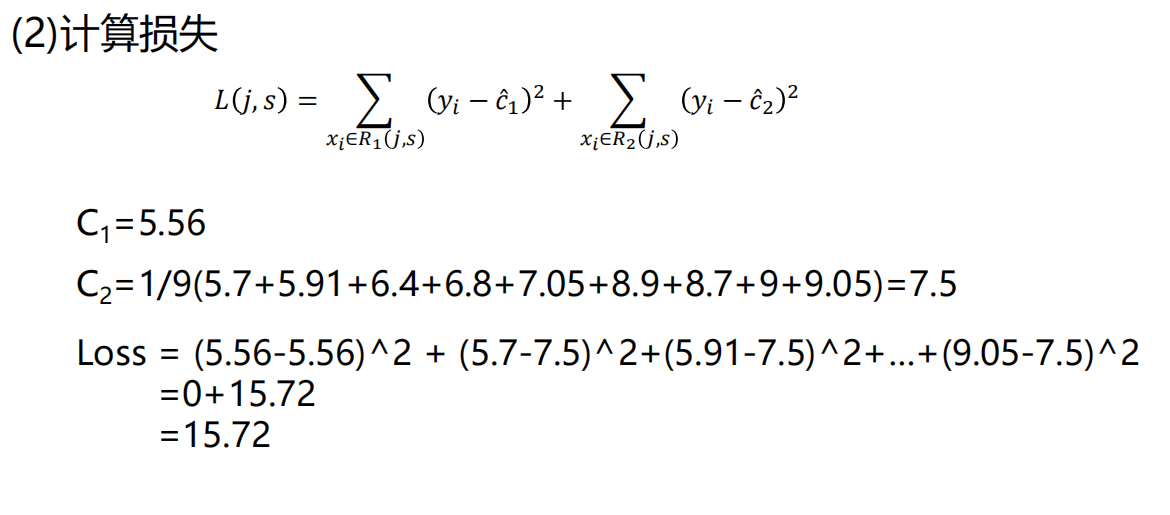
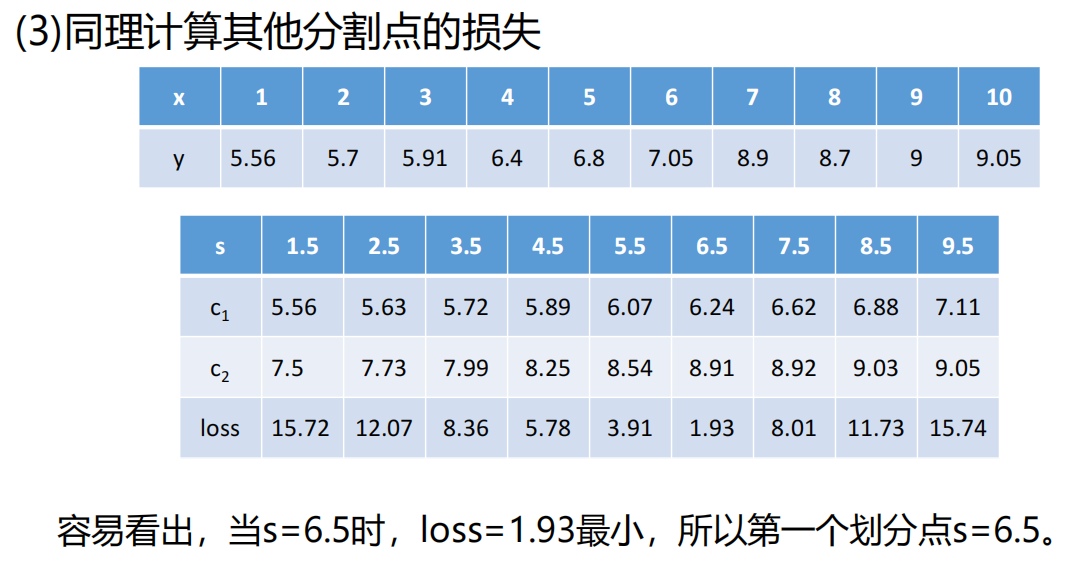
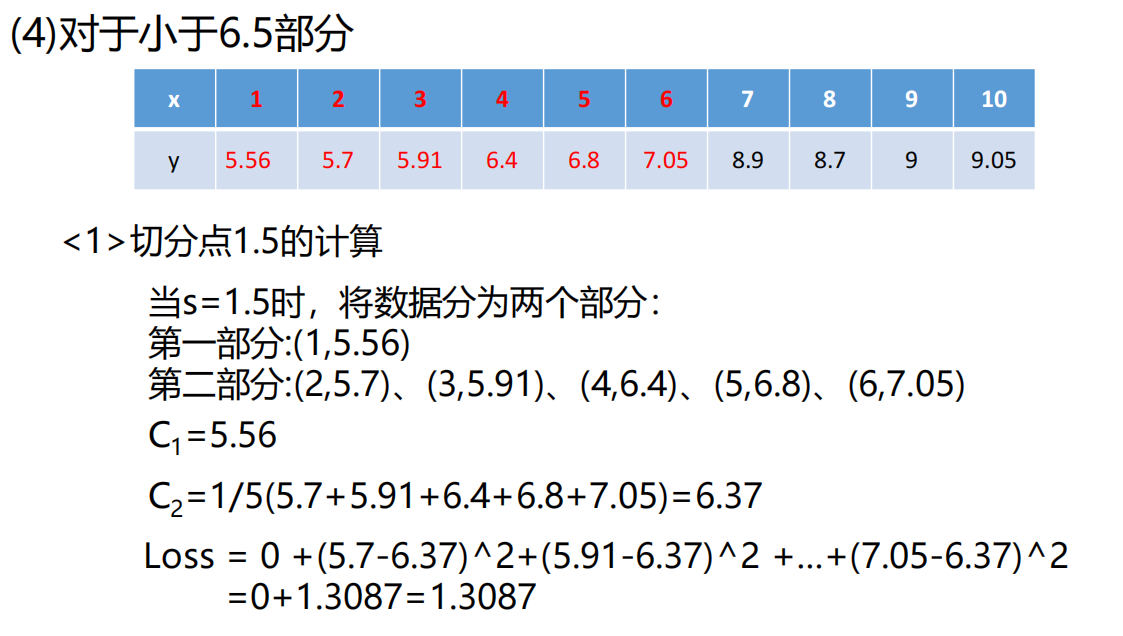
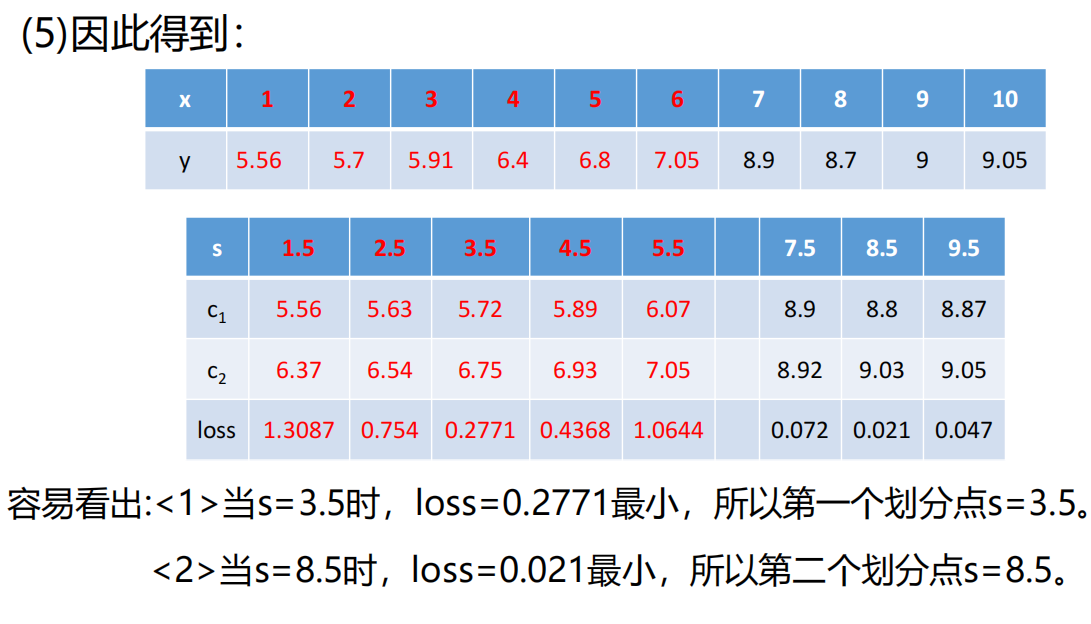
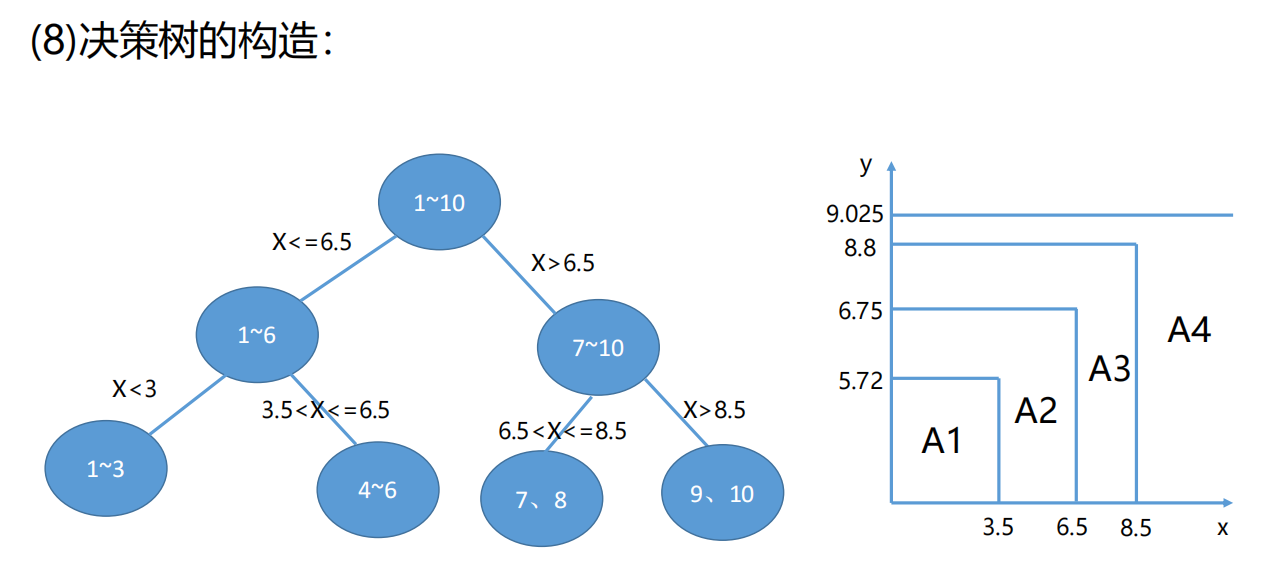
8、sklearn库中决策树之回归树参数问题

class sklearn.tree.DecisionTreeRegressor (criterion='mse' , splitter='best' , max_depth=None , min_samples_split=2 , min_samples_leaf=1 , min_weight_fraction_leaf=0.0 , max_features=None , random_state=None , max_leaf_nodes=None , min_impurity_decrease=0.0 , min_impurity_split=None , presort=False )[source]

1.criterion：节点分裂依据。默认：mse

可选择·mae(平均绝对误差)->使用绝对值

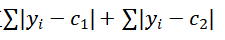
【按默认选择mse即可】

2.splitter:默认best，表示以最优的方式切分节点。决定了树构建过程中的节点分裂策略。值为'best'，意味着在每个节点上，算法会找出最好的分割点来尽量降低信息熵或者减少均方误差。如果设置为'random'，则算法会随机选择一个特征进行分裂。

【按默认选择best即可】

3.max_depth：树的最大深度。过深的树可能导致过拟合。

【通过交叉验证来进行选择】

4.min_samples_split ：默认值是2. 分裂一个内部节点需要的最小样本数，

【含义与分类相同】

5.min_samples_leaf : 默认值是1，叶子节点最少样本数

【含义与分类相同】

6.max_leaf_nodes ：设置最多的叶子节点个数，达到要求就停止分裂【控制过拟合】

【设置此参数之后max_depth失效】★重要

一些方法：

1. apply : 返回预测每个样本的叶子的索引
2. decision_path: 返回树中的决策路径
3. get_depth: 获取树的深度
4. get_n_leaves: 获取树的叶子节点数
5. get_params: 获取此估计器的参数，即前面配置的全部参数信息
6. score: 得到决策树的评判标准R2