ARIMA-LSTM-Prophet 融合模型在股票预测中的应用

哈喽，我是我不是小upper～

今儿咱们就来拆解一个实用案例 ------ 融合 ARIMA、LSTM 与 Prophet 的股票价格趋势三模型预测系统。不过先说明下，咱们重点聚焦模型融合的核心逻辑，属于理论层面的思路分享哦～

股票价格预测的核心痛点在于，它既包含宏观趋势、周期性波动，又有非线性的随机波动，单一模型很难全面覆盖这些特征。就像每个专家都有自己的专长领域，单一模型也各有优劣：

ARIMA 作为经典的时序统计模型，擅长捕捉数据中的线性自回归关系 和平稳性趋势，对规律化的波动拟合很靠谱；
LSTM 作为深度学习中的时序模型，能通过门控机制深度挖掘非线性依赖 和长周期记忆特征，应对复杂的价格突变、趋势转折更有优势；
Prophet 则主打 "可解释性"，能清晰拆解数据中的长期趋势、季节性波动（如日内、周内、年度周期） ，对有明确周期规律的股票走势适配性极高。

正因为单一模型总有 "能力边界"，在不同市场环境下可能掉链子（比如 ARIMA 搞不定非线性突变，LSTM 对周期性的捕捉不如 Prophet 直观），所以三模型融合的思路应运而生。它的核心逻辑特别好理解：就像邀请三位各有所长的专家会诊股票走势 ------ 先让 ARIMA、LSTM、Prophet 各自基于自身优势独立预测未来价格，再通过加权平均的方式将三个预测结果融合成最终输出。这种 "集思广益" 的融合方式，能中和单一模型的偏差，让预测结果更稳健：既降低了个别模型因适配性不足导致的预测方差，又提升了模型在不同市场场景下的泛化能力，比单靠一个模型 "单打独斗" 靠谱得多。

这里必须重点强调一个时间序列预测的 "红线"------ 避免数据泄露！这也是很多刚接触时序预测的同学容易踩的坑。对于股票这类强时序数据，未来的信息（比如明天的价格、后天的市场行情）绝对不能提前被模型 "偷看"------ 如果训练阶段就让模型接触到了后续的信息，哪怕是无意的，也会导致模型预测结果严重失真，看似训练效果极好，实际落地时完全没用。

常见的典型数据泄露场景有这些：

预处理时 "一刀切"：用包含验证集、测试集的数据去拟合标准化、归一化等预处理组件，相当于让模型提前知道了未来数据的分布；
窗口特征构造失误：构建滞后特征（比如用 t 时刻的价格预测 t+1 时刻）时，不小心把 t+1 时刻的真实价格混入 t 时刻的输入特征中；
滞后项使用不当：训练时引入了超出 "历史已知范围" 的未来滞后项，比如用第 10 天的数据训练时，用到了第 11 天的滞后特征；
调参时 "作弊"：把测试集数据用于模型超参数调优，相当于让模型提前适应了测试集的分布，失去了泛化能力的检验意义。

所以在咱们这个三模型融合系统中，会严格遵循 "时间先后" 原则规避数据泄露：所有数据按时间顺序切分（比如用前 80% 做训练集、中间 10% 做验证集、最后 10% 做测试集），所有预处理操作（标准化、特征构造等）都只基于训练集数据拟合，再同步作用于验证集和测试集；模型训练、预测的每一步，都只依赖当前时刻之前的历史已知数据，绝不触碰任何未来信息，确保预测结果的真实性和可靠性。

核心点

给定股票时间序列数据（其中表示第 t 时刻的收盘价，T 为总时间步长），核心目标是基于历史数据进行多步预测 ：已知前 t 时刻的观测值，预测未来 h 步的价格（h≥1，即短期 / 中期趋势预测）。

为确保预测的客观性和泛化能力，严格遵循时间序列数据切分原则（不打乱时间顺序，避免未来信息泄露）：

训练集 Train={x1,...,xTtr}：占比通常为 70%~80%，用于模型核心参数的拟合（如 ARIMA 的阶数、LSTM 的权重、Prophet 的趋势参数等）；
验证集 Val={xTtr+1,...,xTtr+Tval}：占比通常为 10%~15%，用于优化融合权重和少量关键超参（如 LSTM 的窗口大小、Prophet 的傅里叶阶数），不参与模型核心参数的重新训练；
测试集 Test={xTtr+Tval+1,...,xT}：占比通常为 10%~15%，作为 "完全 unseen" 的数据，用于最终评估模型的泛化性能，不参与任何参数调优。

ARIMA 模型

ARIMA（AutoRegressive Integrated Moving Average）是经典的时序统计模型，核心思想是先通过差分使非平稳序列平稳化，再用 AR（自回归）捕捉序列自身的滞后依赖，用 MA（滑动平均）捕捉随机扰动的滞后影响，最终实现对未来趋势的预测。ARIMA 用 ARIMA(p,d,q) 表示：d 次差分后，用 p 阶 AR 模型和 q 阶 MA 模型建模。

1. 平稳性与差分操作

非平稳序列（均值、方差随时间变化）无法直接用 ARMA 建模，因此需要通过差分消除趋势和季节性，得到平稳序列：

一阶差分（d=1）：定义差分算子，若平稳，则；
二阶差分（d=2）：若一阶差分后仍不平稳，继续对差分序列差分：；此时，
通用 d 阶差分：，最终得到平稳序列。

2. ARMA 建模（平稳序列 Zt）

对平稳后的序列，ARMA (p, q) 模型的数学表达式为：

其中：

为 AR 模型的自回归系数（捕捉 Zt 与前 p 步自身的依赖关系）；
为 MA 模型的滑动平均系数（捕捉前 q 步随机扰动对 Zt 的影响）；
为白噪声序列（均值为 0、方差恒定、无自相关的随机扰动）。

3. 预测与逆差分还原

ARIMA 模型的预测分为两步：先对平稳序列做多步预测，再通过逆差分还原为原始序列的预测值，全程采用多步递推法避免数据泄露：

参数拟合 ：基于训练集 Train 的差分序列，通过极大似然估计（MLE）求解、和；
平稳序列多步预测：
- 1 步预测：；
- 2 步预测：；
- 以此类推，后续预测均使用前一步的预测值替代真实值，不依赖未来观测；
逆差分还原 ：将预测的平稳序列还原为原始价格预测：
- 若 d=1：（初始值，训练集最后一个观测值）；
- 若 d=2：，再。

LSTM 模型

LSTM（Long Short-Term Memory）是一种改进的循环神经网络（RNN），通过门控机制（遗忘门、输入门、输出门）解决了传统 RNN 的长序列依赖遗忘问题，能有效捕捉时间序列中的非线性模式和长周期关联，适合股票价格这类复杂波动数据。

1. 输入输出构造

采用滑动窗口法构造训练样本，避免数据泄露：

设定滞后窗口大小为 w（即使用前 w 个时刻的价格预测下一个时刻）；
对训练集，构造样本，其中输入序列，目标值；
模型输入需标准化处理：，其中、仅由训练集计算，避免泄露验证集 / 测试集信息。

2. 门控机制数学表达

LSTM 单元的核心是通过门控调节细胞状态（长期记忆）和隐状态（短期记忆），各模块的数学公式如下（σ 为 sigmoid 激活函数，tanh 为双曲正切激活函数，⊙ 为元素 - wise 乘法）：

遗忘门（Forget Gate） ：决定保留多少历史细胞状态，输出（1 表示完全保留，0 表示完全遗忘）：
输入门（Input Gate） ：决定哪些新信息被存入细胞状态：
候选信息（Candidate Cell State） ：生成待存入细胞状态的新信息：
细胞状态更新 ：结合遗忘门和输入门，更新长期记忆：
输出门（Output Gate） ：决定从细胞状态中输出哪些信息作为隐状态：
隐状态（Short-Term Memory） ：作为当前时刻的输出，传递给下一个时间步：

其中为权重矩阵，为偏置向量，均为模型训练参数。

3. 预测头与多步递推预测

预测头 ：LSTM 单元的隐状态 ht 经过一层线性层映射到预测值：，其中、为线性层参数；
多步预测（避免泄露）：
- 验证集 / 测试集预测采用 "种子窗口 + 迭代预测" 策略：以训练集最后一个窗口为初始输入，预测；
- 下一个窗口输入更新为，预测；
- 迭代至完成验证集 / 测试集的所有步数预测，全程不使用未来真实值。

Prophet 模型

Prophet 是 Facebook 提出的时序预测模型，核心特点是加法可分解、可解释性强、对缺失值和异常值鲁棒，适合有明显趋势和季节性的业务数据（如股票的日内 / 周内 / 年度波动）。其核心假设是时间序列可分解为趋势、季节性、假日和残差四个独立组件的叠加。

1. 加法模型基本形式

Prophet 模型的数学表达式为：

其中：

：趋势项（Trend）：表示序列的长期变化趋势（如线性增长 / 下降、逻辑增长饱和趋势）；
：季节性项（Seasonality）：表示序列的周期性波动（如周周期、年周期），用傅里叶级数逼近；
：假日项（Holidays）：表示特定假日（如春节、国庆）或事件对序列的影响，用 0-1 指示变量建模：（表示第 t 时刻是第 k 个假日，为假日影响系数）；
：残差项（Noise）：模型无法解释的随机扰动。

2. 关键组件细节

趋势项 ：
- 分段线性趋势：，其中为增长率，为截距，通过变点划分不同阶段（每个阶段增长率和截距恒定）；
- 逻辑增长趋势（适用于饱和序列）：，C 为承载能力（序列上限）。
季节性项 s(t) ：用傅里叶级数捕捉非线性周期性，公式为：其中：
- P 为周期（如周周期 P=7，年周期 P=365）；
- N 为傅里叶阶数（N 越大，能捕捉的季节性越复杂，通常取 4~10）；
- 为季节性系数，通过模型拟合得到。

3. 模型拟合与预测

拟合：基于训练集 Train，通过最大后验估计（MAP）求解 g(t)、s(t)、h(t) 的所有参数；
预测：拟合完成后，直接输入未来时间点 t（验证集 / 测试集的时间索引），模型会自动生成趋势、季节性、假日的叠加预测 x^t，无需递推（Prophet 内部已通过趋势延续和季节性重复实现多步预测），且仅依赖训练集信息，无数据泄露。

三模型融合

采用加权平均融合策略，核心思想是利用验证集优化各模型的权重，使融合预测的误差最小化，同时保证权重的物理意义（非负、和为 1）。

1. 权重优化目标

设验证集的样本数为，三个模型在验证集上的预测值分别为：

ARIMA 预测：；
LSTM 预测：；
Prophet 预测：；
验证集真实值：。

优化目标是找到权重，最小化融合预测的均方误差（MSE），约束条件为且：

2. 权重求解方法

先不考虑约束，通过最小二乘求解初始权重：将优化问题转化为矩阵形式，其中，解得；
对进行概率单纯形投影 （Simplex Projection），确保满足非负和归一化约束：投影后权重是初始权重在单纯形上的最近点。

3. 最终融合预测

测试集上的最终预测值为三个模型预测值的加权和：

评价指标

采用三类常用时序预测评价指标，全面衡量模型的预测精度（n=Ttest 为测试集样本数，y^i 为预测值，yi 为真实值）：

1. 均方根误差（RMSE）

衡量预测值与真实值的平均平方偏差，对大误差更敏感，单位与原始数据一致：

2. 平均绝对误差（MAE）

衡量预测值与真实值的平均绝对偏差，对异常值更稳健，单位与原始数据一致：

MAE=n1∑i=1n∣yi−y^i∣

3. 平均绝对百分比误差（MAPE）

衡量预测的相对误差，直观反映预测精度（百分比），加入极小值避免分母为 0：

指标越小表示预测精度越高，其中 RMSE 适合关注整体误差，MAE 适合存在异常值的场景，MAPE 适合需要直观对比相对误差的场景。

完整案例

说我们构造一个类股票 的虚拟价格序列：几何布朗运动（有随机波动）、叠加弱周季节性（方便Prophet学到季节）、中期结构性变化。

数据划分：Train/Val/Test，严格按时间顺序；缩放器仅在训练集拟合；多步递推预测，避免任何未来信息泄露。

三模型：ARIMA（statsmodels）、LSTM（PyTorch实现）、Prophet（prophet库）。

融合：在验证集上优化权重，在测试集评估最终效果。

python 复制代码

import warnings
warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime, timedelta
from math import sqrt

# 统计与时间序列
import statsmodels.api as sm
from statsmodels.tsa.statespace.sarimax import SARIMAX
from prophet import Prophet

# PyTorch
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader

# 1. 随机种子
def set_seed(seed=42):
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)

set_seed(42)

# 2. 生成虚拟**股票**数据
def generate_synthetic_stock(n_days=900, start_date="2023-01-01", seed=42):
    np.random.seed(seed)
    dates = pd.date_range(start=start_date, periods=n_days, freq="D")
    # 几何布朗运动 (GBM)
    dt = 1/252
    mu = 0.08  # 漂移
    sigma = 0.25  # 波动
    prices = [100.0]
    for i in range(1, n_days):
        drift = (mu - 0.5*sigma**2)*dt
        shock = sigma*np.sqrt(dt)*np.random.randn()
        prices.append(prices[-1]*np.exp(drift + shock))
    prices = np.array(prices)

    # 周季节性（弱） + 结构性变化（例如中段波动加剧）
    weekly = 0.5*np.sin(2*np.pi*np.arange(n_days)/7)
    regime = np.ones(n_days)
    regime[int(n_days*0.5):int(n_days*0.7)] *= 1.05  # 中段微升
    regime[int(n_days*0.7):] *= 0.95  # 后段微降

    y = prices * (1 + 0.01*weekly) * regime
    df = pd.DataFrame({"ds": dates, "y": y})
    return df

df = generate_synthetic_stock(n_days=900, start_date="2023-01-01", seed=42)

# 3. 划分训练/验证/测试（时间顺序）
n = len(df)
train_end = int(n*0.7)    # 70% 训练
val_end = int(n*0.85)     # 15% 验证，15% 测试
train_df = df.iloc[:train_end].copy()
val_df = df.iloc[train_end:val_end].copy()
test_df = df.iloc[val_end:].copy()

# 4. 可视化 1：价格曲线 + 分区上色
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(df["ds"], df["y"], color="#1f77b4", label="价格")
ax.axvspan(train_df["ds"].iloc[0], train_df["ds"].iloc[-1], color="#2ca02c", alpha=0.15, label="Train")
ax.axvspan(val_df["ds"].iloc[0], val_df["ds"].iloc[-1], color="#ff7f0e", alpha=0.15, label="Val")
ax.axvspan(test_df["ds"].iloc[0], test_df["ds"].iloc[-1], color="#d62728", alpha=0.15, label="Test")
ax.set_title("图1：整体价格曲线与Train/Val/Test分区", fontsize=14)
ax.legend()
plt.show()

# 5. 可视化 2：滚动均值与滚动波动率（非平稳性）
roll_win = 30
roll_mean = df["y"].rolling(roll_win).mean()
roll_std = df["y"].rolling(roll_win).std()

fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(df["ds"], df["y"], color="#1f77b4", label="价格")
ax.plot(df["ds"], roll_mean, color="#2ca02c", linewidth=2.0, label=f"{roll_win}日滚动均值")
ax.plot(df["ds"], roll_std, color="#e377c2", linewidth=2.0, label=f"{roll_win}日滚动波动率")
ax.set_title("图2：滚动均值与滚动波动率（非平稳性直观）", fontsize=14)
ax.legend()
plt.show()

# 6. 构造数据（缩放器仅用训练集拟合），LSTM窗口
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
y_train = train_df["y"].values.reshape(-1, 1)
scaler.fit(y_train)  # 仅在训练集拟合

# 序列窗口函数（只用于构造训练与验证窗口；多步预测另写）
def make_sliding_windows(series, window=30):
    X, Y = [], []
    for i in range(window, len(series)):
        X.append(series[i-window:i])
        Y.append(series[i])
    return np.array(X), np.array(Y)

# LSTM数据集定义
class SeqDataset(Dataset):
    def __init__(self, X, y):
        self.X = torch.tensor(X, dtype=torch.float32)
        self.y = torch.tensor(y, dtype=torch.float32)

    def __len__(self): return len(self.X)
    def __getitem__(self, idx): return self.X[idx], self.y[idx]

# 7. ARIMA（仅用训练集拟合，多步递推预测Val+Test）
# 为简单起见，我们手动选择几个(p,d,q)中最小AIC的组合，仅在训练集上评估AIC
p_values, d_values, q_values = [0,1,2,3], [0,1], [0,1,2,3]
best_aic = np.inf
best_order = None
train_endog = train_df["y"].values

for p in p_values:
    for d in d_values:
        for q in q_values:
            try:
                model = SARIMAX(train_endog, order=(p, d, q), enforce_stationarity=False, enforce_invertibility=False)
                res = model.fit(disp=False)
                if res.aic < best_aic:
                    best_aic = res.aic
                    best_order = (p, d, q)
            except:
                continue

print("选中的ARIMA阶数(order)为：", best_order, " | 训练AIC=", best_aic)

# 用选中的阶数在训练集拟合，然后对 Val+Test 做多步递推（一次性forecast）
total_horizon = len(val_df) + len(test_df)
arima_model = SARIMAX(train_endog, order=best_order, enforce_stationarity=False, enforce_invertibility=False)
arima_res = arima_model.fit(disp=False)
arima_forecast_all = arima_res.get_forecast(steps=total_horizon).predicted_mean
arima_val_pred = arima_forecast_all[:len(val_df)]
arima_test_pred = arima_forecast_all[len(val_df):]

# 8. Prophet（仅用训练集拟合，多步预测Val+Test）
prophet_model = Prophet(
    yearly_seasonality=False,
    weekly_seasonality=True,
    daily_seasonality=False,
    changepoint_prior_scale=0.05,
    seasonality_mode='additive'
)
prophet_model.fit(train_df[["ds", "y"]])

future_df = pd.DataFrame({
    "ds": pd.date_range(start=val_df["ds"].iloc[0], periods=total_horizon, freq="D")
})
prophet_forecast = prophet_model.predict(future_df)
prophet_pred_all = prophet_forecast["yhat"].values
prophet_val_pred = prophet_pred_all[:len(val_df)]
prophet_test_pred = prophet_pred_all[len(val_df):]

# 9. LSTM（PyTorch）：训练 + 多步递推预测（避免未来真值）
window = 30
# 训练集滑动窗口（注意：缩放仅用训练集拟合）
y_train_scaled = scaler.transform(y_train)
X_train, Y_train = make_sliding_windows(y_train_scaled, window=window)

train_dataset = SeqDataset(X_train.reshape(-1, window, 1), Y_train.reshape(-1, 1))
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)

# 定义LSTM网络
class LSTMRegressor(nn.Module):
    def __init__(self, input_size=1, hidden_size=64, num_layers=2, dropout=0.2):
        super().__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers=num_layers, batch_first=True, dropout=dropout)
        self.fc = nn.Linear(hidden_size, 1)

    def forward(self, x):
        # x: (B, T, 1)
        out, _ = self.lstm(x)
        out = out[:, -1, :]
        out = self.fc(out)
        return out

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = LSTMRegressor().to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

# 训练（仅用训练集）
epochs = 40
model.train()
for epoch in range(epochs):
    losses = []
    for xb, yb in train_loader:
        xb, yb = xb.to(device), yb.to(device)
        optimizer.zero_grad()
        pred = model(xb)
        loss = criterion(pred, yb)
        loss.backward()
        optimizer.step()
        losses.append(loss.item())
    if (epoch+1) % 10 == 0:
        print(f"[LSTM] epoch {epoch+1}/{epochs} | loss={np.mean(losses):.6f}")

# 多步递推预测Val+Test：从训练末尾窗口出发，一步步喂入预测结果
def lstm_multistep_forecast(model, last_train_series, horizon, window, scaler):
    """
    last_train_series: 训练集的原始y（未缩放），用于取最后窗口
    horizon: 需要预测的步数（Val+Test总长度）
    """
    model.eval()
    history = last_train_series.copy().astype(float).reshape(-1, 1)
    preds = []
    with torch.no_grad():
        for _ in range(horizon):
            # 取最后window步（原始尺度，先缩放）
            window_series = history[-window:]
            window_scaled = scaler.transform(window_series)
            x = torch.tensor(window_scaled.reshape(1, window, 1), dtype=torch.float32).to(device)
            yhat_scaled = model(x).cpu().numpy().reshape(-1, 1)
            # 反缩放到原始尺度
            yhat = scaler.inverse_transform(yhat_scaled)[0, 0]
            preds.append(yhat)
            # 预测值作为下一步的输入
            history = np.vstack([history, [[yhat]]])
    return np.array(preds)

last_train_series = train_df["y"].values
lstm_pred_all = lstm_multistep_forecast(model, last_train_series, horizon=total_horizon, window=window, scaler=scaler)
lstm_val_pred = lstm_pred_all[:len(val_df)]
lstm_test_pred = lstm_pred_all[len(val_df):]

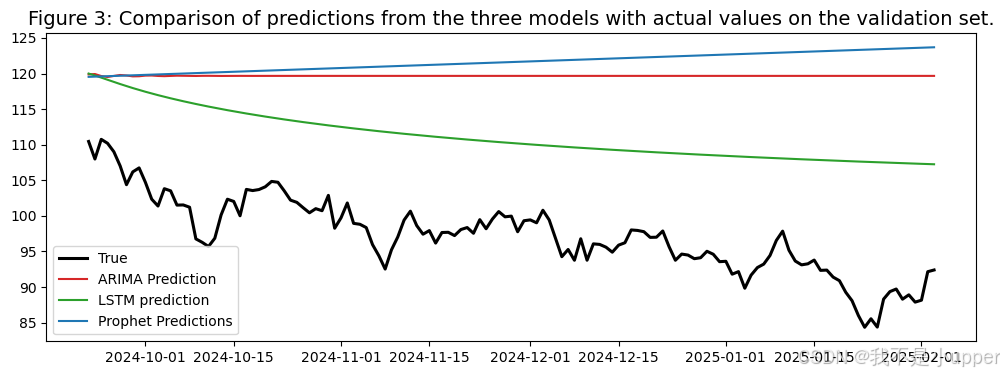
# 10. 可视化 3：验证集上三模型预测对比真实值
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(val_df["ds"], val_df["y"].values, color="#000000", linewidth=2.2, label="真实")
ax.plot(val_df["ds"], arima_val_pred, color="#d62728", label="ARIMA预测")
ax.plot(val_df["ds"], lstm_val_pred, color="#2ca02c", label="LSTM预测")
ax.plot(val_df["ds"], prophet_val_pred, color="#1f77b4", label="Prophet预测")
ax.set_title("图3：验证集上三模型预测对比真实值", fontsize=14)
ax.legend()
plt.show()

# 11. 在验证集上拟合融合权重（约束：非负、和为1）
def simplex_projection(v):
    """将向量v投影到概率单纯形：w>=0, sum(w)=1。"""
    n = len(v)
    u = np.sort(v)[::-1]
    cssv = np.cumsum(u)
    rho = np.where(u + (1.0 - cssv) / (np.arange(n) + 1) > 0)[0][-1]
    theta = (cssv[rho] - 1) / (rho + 1.0)
    w = np.maximum(v - theta, 0)
    return w

# 验证集矩阵 X_val=[arima, lstm, prophet], y_val
X_val = np.vstack([arima_val_pred, lstm_val_pred, prophet_val_pred]).T  # shape: (n_val, 3)
y_val = val_df["y"].values

# 最小二乘解（无约束），再投影到单纯形
w_ls, _, _, _ = np.linalg.lstsq(X_val, y_val, rcond=None)
w_ens = simplex_projection(w_ls)
w_ens = w_ens / w_ens.sum()

print("融合权重（在验证集上学得）:", w_ens, "  （顺序：[ARIMA, LSTM, Prophet]）")

# 12. 测试集预测与评估（融合）
X_test = np.vstack([arima_test_pred, lstm_test_pred, prophet_test_pred]).T
y_test = test_df["y"].values
y_ens_test = X_test @ w_ens

def rmse(y_true, y_pred): return sqrt(np.mean((y_true - y_pred)**2))
def mae(y_true, y_pred): return np.mean(np.abs(y_true - y_pred))
def mape(y_true, y_pred, eps=1e-8): return np.mean(np.abs((y_true - y_pred)/(y_true+eps))) * 100

print("\n=== 测试集指标（单模型与融合） ===")
for name, pred in [
    ("ARIMA", arima_test_pred),
    ("LSTM", lstm_test_pred),
    ("Prophet", prophet_test_pred),
    ("Ensemble", y_ens_test)
]:
    print(f"{name:8s} | RMSE={rmse(y_test,pred):.4f}  MAE={mae(y_test,pred):.4f}  MAPE={mape(y_test,pred):.2f}%")

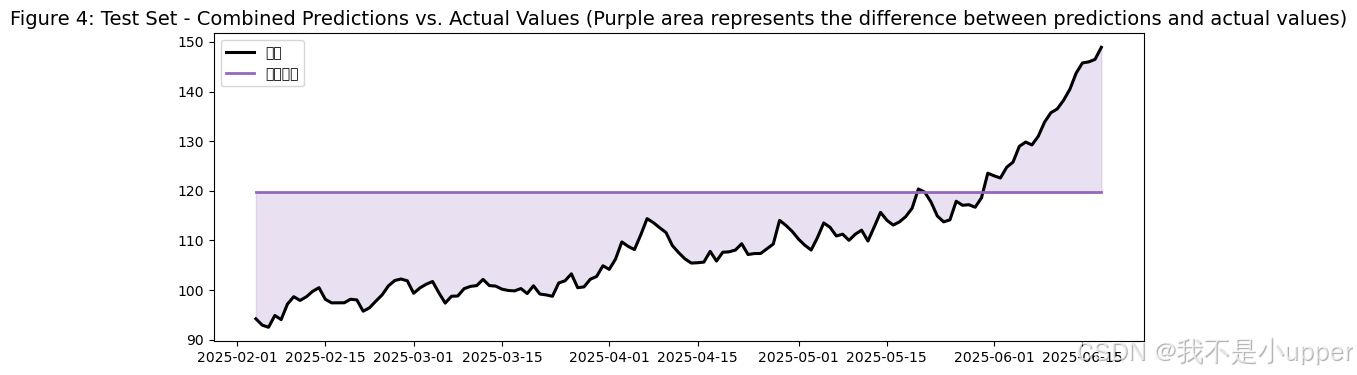
# 13. 可视化 4：测试集 融合预测 vs 真实值
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(test_df["ds"], y_test, color="#000000", linewidth=2.2, label="真实")
ax.plot(test_df["ds"], y_ens_test, color="#9467bd", linewidth=2.0, label="融合预测")
ax.fill_between(test_df["ds"], y_ens_test, y_test, color="#9467bd", alpha=0.2)
ax.set_title("图4：测试集 融合预测 vs 真实值（紫色区域为预测-真实差）", fontsize=14)
ax.legend()
plt.show()


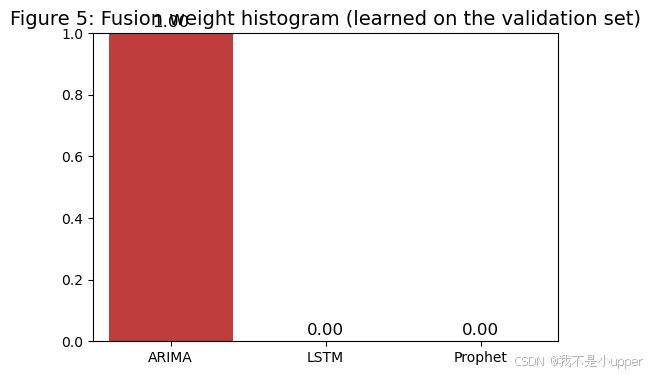
# 14. 可视化 5：融合权重柱状图（直观解释融合）
fig, ax = plt.subplots(figsize=(6, 4))
labels = ["ARIMA", "LSTM", "Prophet"]
colors = ["#d62728", "#2ca02c", "#1f77b4"]
sns.barplot(x=labels, y=w_ens, palette=colors, ax=ax)
ax.set_ylim(0, 1.0)
ax.set_title("图5：融合权重柱状图（在验证集学得）", fontsize=14)
for i, v in enumerate(w_ens):
    ax.text(i, v + 0.02, f"{v:.2f}", ha='center', color='black', fontsize=12)
plt.show()


# 15. 可视化 6：测试集各模型残差对比
fig, ax = plt.subplots(figsize=(12, 4))
errors = {
    "ARIMA": y_test - arima_test_pred,
    "LSTM": y_test - lstm_test_pred,
    "Prophet": y_test - prophet_test_pred,
    "Ensemble": y_test - y_ens_test,
}
for name, err in errors.items():
    ax.plot(test_df["ds"], err, label=name)
ax.axhline(0, color="black", linewidth=1)
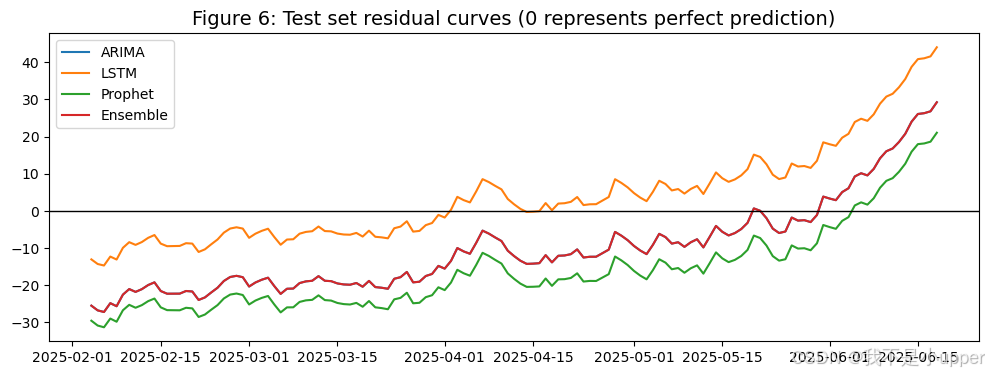
ax.set_title("图6：测试集 残差曲线（0为完美预测）", fontsize=14)
ax.legend()
plt.show()

时间切分严格按ds时间先后：Train -> Val -> Test。

缩放器MinMaxScaler仅在训练集y上拟合（fit），然后对Val/Test使用transform，不再refit，避免信息泄露。

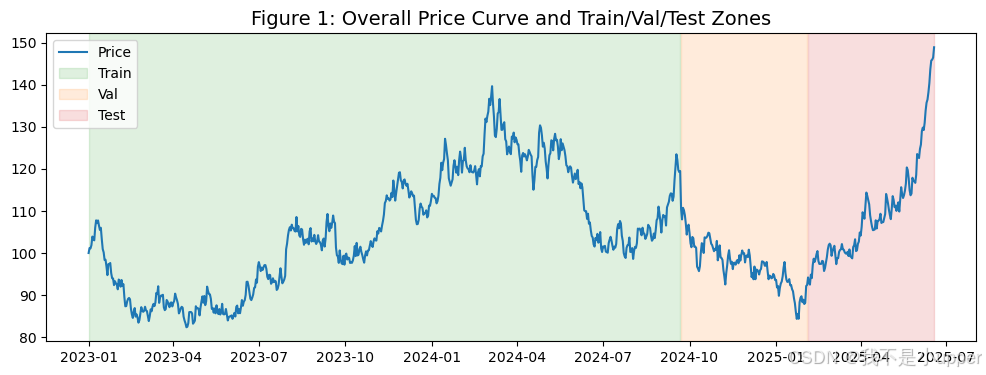
ARIMA/Prophet/LSTM均采用多步递推预测：仅用训练集拟合模型，一次性预测Val+Test的未来H步。这样不会用到Val/Test的真实值作为输入，避免泄露。

融合权重只在验证集上优化；最终报告测试集指标，测试集在模型训练与权重学习阶段完全不可见。

LSTM预测时从训练末尾窗口开始，逐步把自己的预测值作为下一步输入，不用任何未来真值（这点实践很重要，很多错误实现会不小心用到了未来真值，从而虚高验证/测试表现）。

指标（RMSE/MAE/MAPE）均在测试集上评估，真实反映泛化性能。

可视化分析：

看图3（验证期）：谁更贴近黑色真实曲线？这会影响融合权重分布。比如如果LSTM更贴合非线性跃迁，它的权重就可能较大；Prophet在存在周季节规律时也会分到一定权重；ARIMA对短期线性结构较敏感。

看图4（测试期）：紫色融合预测与黑色真实是否更接近？通常融合的泛化更稳健，峰谷偏差相对单模型会降低。

看图5（权重）：理解谁说了更多话 。权重不是固定真理：不同数据、分割、任务下会变。权重来自验证集拟合，你可以把它理解为在近期（验证期）表现更好的模型得到更大权重。

看图6（残差）：理想情况下，融合残差在0附近较均匀、波动幅度较小。这意味着系统综合了不同模型的优点，减少了系统性偏差与极端误差。

更先进的融合：用非负约束的线性回归、Lasso、或高斯过程/树模型在验证集上做元学习。但务必注意：元学习器只能在验证集上训练，测试集只能评估，避免泄露。

动态权重，可以随时间更新权重，如滑动窗口上实时再学习权重。但每次更新只能用已经发生的数据。

特征扩充，在LSTM前加入更多输入特征（成交量、技术指标如MACD、RSI等）。同样，特征构造时严禁用未来数据。

ARIMA改进，做更系统的(p,d,q)网格或使用auto_arima（pmdarima），但调参要仅用训练或通过滚动验证管控。

Prophet优化，根据数据长度合适地设置seasonality（如周/月/年）与changepoint_prior_scale。

总结

我们用ARIMA（线性自回归）、LSTM（非线性长依赖）、Prophet（趋势+季节性）三种风格互补的模型，采用严格的时间切分和多步递推；

在验证集上学习非负且和为1的融合权重，最后在测试集上评估；

大家有机会，可以在自己的业务中，尝试一下~