今天我们要认识一位特别的朋友------逻辑回归算法 。别看它名字里带着"回归",它可是分类问题中的明星选手呢!
想象一下,你面前有两扇门,一扇通向糖果屋,一扇通向图书馆。根据你的心情、时间和目的,你需要快速决定走哪一扇门。逻辑回归就像一个聪明的向导,它能根据你给出的各种线索(比如"我现在饿不饿"、"有没有半小时空闲"),快速计算出你选择糖果屋的概率是80%还是20%,从而帮你做出"去"或"不去"的决策。
在日常生活中,这样的"是非题"无处不在:这封邮件是垃圾邮件还是正常邮件 ?这张图片里的动物是猫还是狗 ?这位患者的化验结果提示患病还是健康?逻辑回归就是专门解决这类"二选一"问题的得力工具。
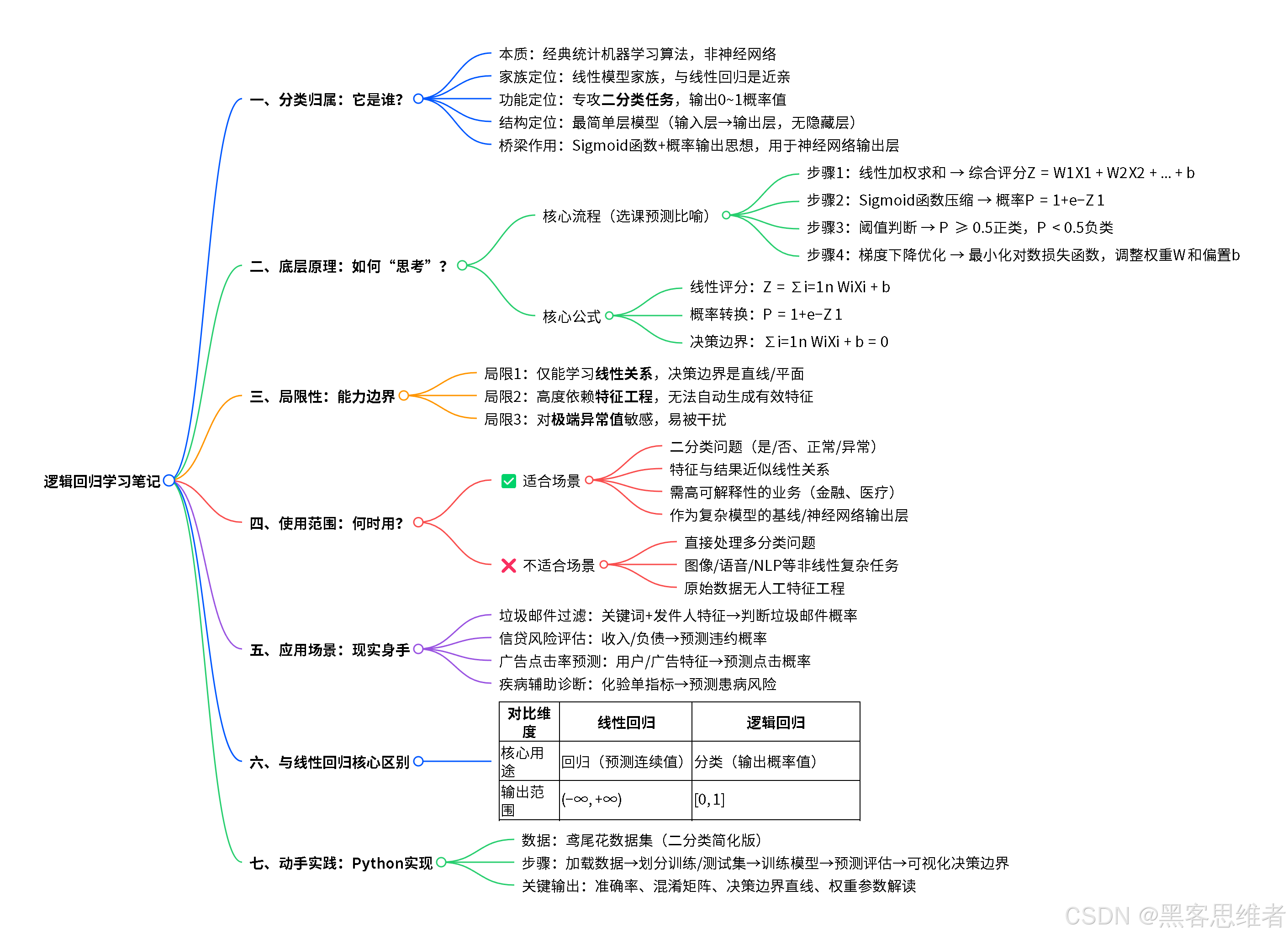
一、 分类归属:它到底是谁?
首先,我们来给逻辑回归"上户口"。这里有一个非常重要的澄清点,也是初学者最容易困惑的地方:
逻辑回归本质上不是一个神经网络,而是一个独立的、经典的机器学习算法。
为了方便你理解它在AI大家庭中的位置,我们可以用下图来梳理它的"血缘关系":
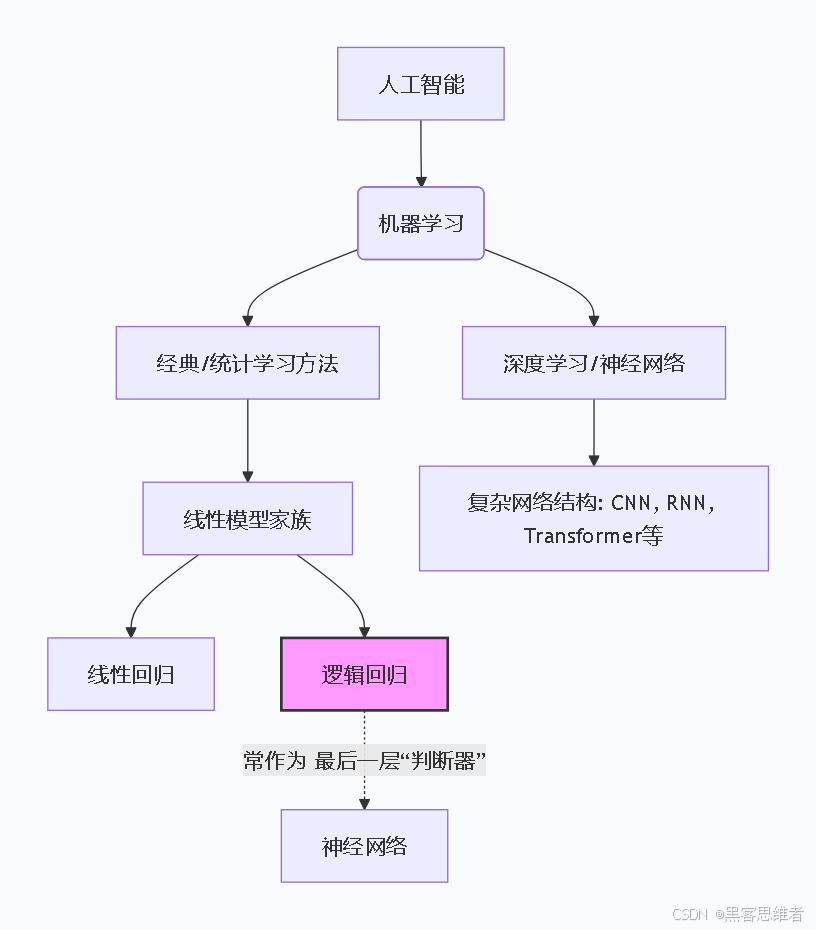
从这张"族谱"我们可以清楚地看到:
- 从家族看 :逻辑回归属于机器学习 领域下的经典统计学习方法 ,与线性回归是"近亲",都出自线性模型家族 。它比深度神经网络(如CNN、RNN)更早被提出,结构也简单得多。
- 从功能看 :它是专门为解决二分类 任务而设计的。它的核心任务是:给定输入数据,输出一个介于0和1之间的概率值,代表属于某个类别的可能性。
- 从结构看 :你可以把它理解为一个超级简化版的单层神经网络。它只有"输入层"和"输出层",没有深度学习模型中那些复杂的"隐藏层"。它的"神经元"就是一个简单的数学公式。
- 重要的桥梁作用 :尽管逻辑回归本身不是深度神经网络,但它的核心思想------用概率表示分类结果 以及使用Sigmoid激活函数 ------被广泛用于各种复杂神经网络的最后一层,专门负责将前面网络提取到的复杂特征,最终转化为一个清晰的分类判断。所以,学好逻辑回归是理解更高级AI模型的坚实基础。
简单来说,如果把复杂的深度神经网络比作能谱写交响乐的音乐大师,那么逻辑回归就像是一个能精准判断"这个音是Do还是Re"的调音器。它虽简单,却至关重要。
二、 底层原理:它是如何"思考"的?
让我们用一个完整的比喻故事,拆解逻辑回归的工作流程。
生活化比喻:学生选课预测系统
假设你是一个"课程推荐导师",要预测一个新学生是否会选择你的"AI科普课"。你手头有每个学生的两条信息:
- 线索X₁:他对科技的感兴趣程度(0-10分)。
- 线索X₂:他每周的课余空闲时间(0-10分)。
你的大脑会做如下推理:
第一步:综合打分(线性加权求和)
你会下意识地给不同线索分配重要性。比如,你觉得"兴趣"比"时间"更重要,于是在心里给"兴趣"打了权重W₁=3分 ,给"时间"打了权重W₂=1分 。同时,你发现即使一个学生兴趣和时间都一般,也可能因为你的课程口碑好而来,这个基础吸引力就是偏置B= -2分。
对于一个兴趣=8、时间=5的学生,你的综合评分Z 就是:
Z=(兴趣∗3)+(时间∗1)+(基础吸引力)=(8∗3)+(5∗1)+(−2)=27分Z = (兴趣 * 3) + (时间 * 1) + (基础吸引力) = (8*3) + (5*1) + (-2) = 27分Z=(兴趣∗3)+(时间∗1)+(基础吸引力)=(8∗3)+(5∗1)+(−2)=27分
第二步:概率转化(Sigmoid函数 - 魔法压缩器)
如果直接看27分,我们很难判断。这个分数是"极高可能选课"还是"一般可能"呢?这时你需要一个魔法压缩器(Sigmoid函数) ,它的魔力是把任何分数(正无穷大到负无穷大)都平滑地压缩到0和1之间,变成一个完美的概率值。
这个魔法公式长这样:
概率P=1/(1+e(−Z))概率 P = 1 / (1 + e^(-Z))概率P=1/(1+e(−Z))
e是一个数学常数(约2.718)。Z就是我们上一步算出的综合评分。
我们不需要记住公式,只需要知道它的魔法效果:
- 当
Z是很大的正数(比如27),e^(-Z)就非常小,P就非常接近1(例如0.999),代表"几乎肯定会选课"。 - 当
Z是很大的负数(比如-10),e^(-Z)就非常大,P就非常接近0(例如0.000),代表"几乎肯定不会选课"。 - 当
Z为0时,P正好等于0.5,代表"完全不确定,五五开"。
把我们的Z=27代进去,计算后P≈0.999。恭喜!你预测这个学生有99.9%的概率会选择你的课。
第三步:做出决策(设定阈值)
有了概率P,最后一步就是拍板。通常我们设定一个阈值 ,比如0.5。
- 如果
P >= 0.5,我们就预测学生"会选课"(输出1)。 - 如果
P < 0.5,我们就预测"不会选课"(输出0)。
核心逻辑图示:

第四步:如何学习?------ 不断试错,优化权重
一开始,导师你给的权重(W₁=3, W₂=1, B=-2)可能是瞎猜的。那怎么找到最准的权重呢?逻辑回归通过学习历史数据来优化。
- 收集数据:你找来100个过去学生的记录(他们的兴趣、时间分数,以及他们最终是否选课的真实结果)。
- 预测与对比:用你当前的权重,对这100个学生逐个预测,算出每个预测的概率P。
- 计算损失 :比较你的预测概率和真实结果(是1还是0)之间的差距。如果预测得很离谱(比如真实选了课,你却只算出P=0.1),差距就很大。这个差距用一个叫对数损失函数的公式来量化。
- 优化调整 :就像一个迷宫的寻宝游戏,损失函数告诉你现在的位置离宝藏(最优权重)有多远。逻辑回归使用一种叫梯度下降 的方法,它分析每个权重(W₁, W₂, B)对总损失"贡献"了多少错误,然后沿着减少错误最快的方向,微调这些权重。
- 循环往复 :重复步骤2-4成千上万次,直到你的权重调整到能让总损失最小,也就是预测得最准为止。
核心公式(了解即可):
- 线性部分 :
Z = W₁X₁ + W₂X₂ + ... + WₙXₙ + b(n是特征数量) - Sigmoid函数 :
P = 1 / (1 + e^(-Z)) - 决策边界 :
W₁X₁ + W₂X₂ + ... + WₙXₙ + b = 0(这条"线"或"面"就是划分两个类别的边界)
三、 局限性:它并非万能
逻辑回归虽然强大且经典,但也有它的"能力边界"。理解它的局限,才能更好地使用它。
-
"一根筋"的直线思维
局限 :逻辑回归最核心的局限在于,它只能学习线性关系 。它的决策边界永远是一条直线(二维时)或一个平面(高维时)。
为什么? 回顾它的公式,决策边界是W₁X₁ + W₂X₂ + b = 0,这本身就是一个线性方程。它就像一把锋利的直尺 ,只能画出笔直的分割线。
后果:如果两类数据在图上像螺旋一样交织在一起,或者呈环状分布(一个圈在里面,一个圈在外面),这把"直尺"无论如何也画不出一条直线把它们完美分开,它的表现就会很差。 -
对特征很"挑剔"
局限 :它的性能非常依赖于特征工程 。你需要提供足够好、有区分度的特征给它。
为什么? 逻辑回归自己不会自动创造新的特征组合。例如,要预测房子是否昂贵,如果只给它"长度"和"宽度"两个特征,它学到的就是"长度和宽度越大,越可能贵"。但如果最相关的特征是"面积"(长度×宽度),逻辑回归自己想不到这一点,需要你事先计算好"面积"这个新特征喂给它。
后果:在图像、语音等领域,原始数据(像素、声波)与最终结果的关系极其复杂、非线性,逻辑回归几乎无法直接处理,因为它无法从海量像素中自动找到"边缘"、"纹理"这些有效特征。 -
容易受"极端分子"影响
局限 :如果数据中存在非常极端的异常值(比如在一群普通客户里混入了一个超级富豪的信贷记录),逻辑回归为了拟合这个极端点,可能会过度调整自己的决策边界,从而影响对大多数普通样本的判断准确性。
四、 使用范围:何时该请它出马?
了解了它的特点,我们就能知道什么场合最适合邀请这位"判断题大师"登场。
适合用它解决的问题(它的"舒适区"):
- 问题类型 :典型的二分类问题。输出结果是"是/否"、"成功/失败"、"正面/负面"等。
- 数据关系 :特征与最终结果之间的关系大致是线性的,或可以通过特征工程转化为近似线性。
- 需求 :模型需要具备良好的可解释性。逻辑回归的权重(W)直接反映了特征的重要性(正权重促进,负权重抑制),这在金融、医疗等需要解释决策原因的领域至关重要。
- 场景 :作为更复杂模型的基准模型。在尝试复杂算法前,先用简单的逻辑回归建立一个性能基线。
- 场景 :作为深度学习网络的最后一道关卡(输出层),负责将前面提取的复杂特征转化为最终的概率输出。
不适合用它解决的问题(它的"知识盲区"):
- 多分类问题(直接处理):如识别手写数字(0-9共10类)。虽然可以通过一些技巧(如"一对多")改造,但非其专长。
- 高度复杂的非线性问题:如图像识别(猫、狗、车)、自然语言理解、语音识别。
- 需要自动特征发现的问题:直接从原始、未经处理的复杂数据(如图像像素、文本序列)中学习。
五、 应用场景:看看它在现实中的身手
逻辑回归在我们的数字生活中无处不在,以下是一些鲜活的例子:
-
垃圾邮件过滤器
- 作用:判断一封新邮件是"垃圾邮件"还是"正常邮件"。
- 工作方式:系统会提取邮件的特征,如:是否包含"免费"、"获奖"等关键词(特征X₁, X₂...),发件人是否在通讯录(Xₙ)。逻辑回归根据这些特征的权重进行计算,输出这是垃圾邮件的概率P。如果P > 0.95(阈值可能更高,以防误杀重要邮件),则将其扔进垃圾箱。
-
信贷风险评估
- 作用:银行判断是否应该给一名申请人发放贷款。
- 工作方式 :输入特征包括:申请人的年龄、收入、职业、信用历史、负债情况等。逻辑回归模型会学习历史贷款数据中,哪些特征组合容易导致违约。当新申请人提交资料时,模型会计算其违约概率P。如果P过高(超过银行设定的风险阈值),则可能拒绝贷款或降低额度。因为模型权重可解释,银行可以告诉申请人:"您的申请被拒,主要是因为年收入偏低且现有负债较高。"
-
在线广告点击率预测
- 作用:预测一个用户是否会点击网页上展示的某条广告。
- 工作方式 :特征包括:用户的性别、年龄、所在地、历史点击记录,以及广告的商品类别、展示位置、文案等。逻辑回归模型实时计算点击概率P。广告平台会优先向用户展示P值最高的广告,从而实现流量价值和用户体验的最大化。这也是为什么你总觉得广告"猜你喜欢"的原因之一。
-
疾病辅助诊断
- 作用:根据患者的检查指标,辅助医生判断其患某种疾病(如糖尿病)的风险。
- 工作方式 :输入特征为患者的化验单数据:血糖值、血压、BMI指数、年龄等。逻辑回归模型基于大量历史病例数据训练,能够输出当前患者患病的风险概率P。医生可以结合此概率和临床经验,做出更高效、更精准的诊断决策。其可解释性也便于医生和患者理解判断依据。
线性回归 vs 逻辑回归:核心区别对比表
| 对比维度 | 线性回归 | 逻辑回归 |
|---|---|---|
| 核心用途 | 解决回归问题:预测连续型数值(如销量、房价、温度、收入) | 解决分类问题:预测离散型类别(如二分类:是否患病/是否违约;多分类:图片类别/用户标签) |
| 输出结果 | 输出任意实数(范围:-∞~+∞),直接对应预测的数值结果 | 输出0~1之间的概率值(二分类):如"患病概率0.8",再通过阈值(如0.5)判定类别(≥0.5=患病,<0.5=健康);多分类则输出各类别概率之和为1 |
| 模型本质 | 线性拟合:找一条直线/平面,最小化真实值与预测值的误差(如均方误差) 公式:y=w1x1+w2x2+...+wnxn+by = w_1x_1 + w_2x_2 + ... + w_nx_n + by=w1x1+w2x2+...+wnxn+b(y为连续值) | 非线性转换的线性模型:先做线性计算,再通过Sigmoid函数(二分类)将结果映射到0~1区间 公式:P=11+e−(w1x1+...+wnxn+b)P = \frac{1}{1+e^{-(w_1x_1 + ... + w_nx_n + b)}}P=1+e−(w1x1+...+wnxn+b)1(P为某类别的概率) |
| 损失函数 | 均方误差(MSE):Loss=1n∑i=1n(yi−y^i)2Loss = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2Loss=n1∑i=1n(yi−y^i)2(聚焦数值误差最小) | 对数似然损失(对数损失):Loss=−1n∑i=1n[yiln(P^i)+(1−yi)ln(1−P^i)]Loss = -\frac{1}{n}\sum_{i=1}^n [y_i\ln(\hat{P}_i) + (1-y_i)\ln(1-\hat{P}_i)]Loss=−n1∑i=1n[yiln(P^i)+(1−yi)ln(1−P^i)](聚焦分类概率的准确性) |
| 假设前提 | 1. 特征与目标值呈线性关系; 2. 残差(预测误差)服从正态分布; 3. 无多重共线性(可选) | 1. 特征与对数几率(ln(P1−P)\ln(\frac{P}{1-P})ln(1−PP))呈线性关系; 2. 样本相互独立; 3. 无完全多重共线性 |
| 适用场景示例 | 预测商品销量、房价走势、学生考试分数、每月用电量 | 预测用户是否流失、邮件是否为垃圾邮件、肿瘤是否为恶性、信贷是否违约 |
| 模型解读 | 系数表示"特征每变化1单位,目标值平均变化多少"(如定价系数-2.5:定价涨1元,销量降2.5千件) | 系数表示"特征每变化1单位,对数几率的变化量"(需转换为优势比解读:如系数0.8,优势比e0.8≈2.22e^{0.8}≈2.22e0.8≈2.22,表示该特征使"正类概率"提升2.22倍) |
| 是否可处理非线性问题 | 原生不可,需手动添加非线性特征(如平方项、交叉项) | 原生不可,需结合特征工程(如多项式特征)或集成方法(如逻辑回归+决策树特征) |
补充说明
- 线性回归:"我算的是'具体数字',比如预测这房子值120万,那就是120万";
- 逻辑回归:"我算的是'可能性',比如这房子有80%概率是刚需房,20%概率是改善房,最后判定它是刚需房"。
两者虽都带"回归",但核心目标完全不同------一个求"数值准",一个求"分类对"。
六、 动手实践:用Python实现一个简单的逻辑回归
理论说了这么多,我们来点实际的!下面是一个使用Python的scikit-learn库,对经典的鸢尾花数据集进行二分类预测的完整示例。即使你没写过代码,也可以通过注释理解每一步在做什么。
python
# 导入必要的工具包
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import seaborn as sns
# 1. 加载数据:我们使用著名的鸢尾花数据集,但为了二分类,只取其中两个品种
iris = datasets.load_iris()
# 只取前100个样本(对应品种0和1,品种2去掉),特征只取前两个(萼片长度和宽度)方便画图
X = iris.data[:100, :2] # 特征矩阵:100个样本,每个样本2个特征
y = iris.target[:100] # 目标标签:0或1
print(f"数据集形状:特征{X.shape}, 标签{y.shape}")
# 2. 划分数据:一部分用于训练模型,一部分用于测试模型效果,保证公平
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
print(f"训练集样本数:{len(X_train)}, 测试集样本数:{len(X_test)}")
# 3. 创建并训练逻辑回归模型
# 创建逻辑回归"机器"
model = LogisticRegression()
# 把训练数据喂给机器,让它学习规律
model.fit(X_train, y_train)
# 4. 使用训练好的模型进行预测
y_pred = model.predict(X_test) # 预测测试集的类别(0或1)
y_pred_proba = model.predict_proba(X_test) # 预测测试集的概率(属于0和1的概率各是多少)
print("\n测试集前5个样本的预测结果:")
for i in range(5):
print(f" 样本{i}: 真实类别={y_test[i]}, 预测类别={y_pred[i]}, 属于类别0的概率={y_pred_proba[i][0]:.3f}, 属于类别1的概率={y_pred_proba[i][1]:.3f}")
# 5. 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
print(f"\n模型在测试集上的准确率:{accuracy:.2%}")
# 绘制混淆矩阵,看看具体错在哪
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=iris.target_names[:2], yticklabels=iris.target_names[:2])
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.title('混淆矩阵')
plt.show()
# 6. 可视化决策边界和数据点(这是理解逻辑回归的关键!)
# 创建网格来绘制决策边界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
# 用模型预测整个网格上每个点的类别
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 开始画图
plt.figure(figsize=(10, 6))
# 画出决策区域
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Paired)
# 画出训练数据点
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, edgecolors='k', cmap=plt.cm.Paired, label='训练集', s=60, marker='o')
# 画出测试数据点,并用形状区分
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolors='k', cmap=plt.cm.Paired, marker='s', s=80, label='测试集', alpha=0.7)
# 标记出预测错误的点
for i in range(len(X_test)):
if y_test[i] != y_pred[i]:
plt.scatter(X_test[i, 0], X_test[i, 1], s=150, facecolors='none', edgecolors='red', linewidths=2, label='预测错误' if i==0 else "")
plt.xlabel(iris.feature_names[0]) # 萼片长度
plt.ylabel(iris.feature_names[1]) # 萼片宽度
plt.title('逻辑回归分类结果与决策边界')
plt.legend()
plt.show()
print("\n模型参数解读:")
print(f" 学到的权重 (W): {model.coef_[0]}") # 对应两个特征的重要性
print(f" 学到的偏置 (b): {model.intercept_[0]:.3f}")
print(" 决策边界方程: {:.3f} * 萼片长度 + {:.3f} * 萼片宽度 + {:.3f} = 0".format(model.coef_[0][0], model.coef_[0][1], model.intercept_[0]))运行这段代码,你会看到:
- 数字结果:模型的准确率,以及每个测试样本的预测详情。
- 混淆矩阵:一张图清晰展示预测对了多少,具体哪些类别被混淆了。
- 决策边界图 :这是最直观的部分!你会看到一条直线将两种颜色的点(代表两种花)分开。这条线就是逻辑回归学到的"是非分界线"。位于线一侧的点被预测为类别0,另一侧的被预测为类别1。红色圈出的点就是预测错误的样本。
通过这个实践,你将亲眼看到逻辑回归如何用一条直线(决策边界)来划分世界,并深刻理解它的工作原理和局限性。
总结
逻辑回归,这位AI世界的"是非判断题大师",其核心价值 在于:用简洁、可解释的线性模型,为二分类问题提供一个坚实的概率化解决方案。
它就像你学习人工智能旅程中的第一把钥匙。虽然它不能直接打开图像识别、自然语言处理那些华丽的宫殿大门,但它教会了你最重要的思维模式:如何将现实问题转化为数学特征,如何用概率来表达不确定性,以及如何通过优化来逼近真理。
记住它的特点:擅长线性二分类、需要好特征、结果易解释。理解并掌握逻辑回归,你便为后续学习更强大的神经网络(如CNN、RNN)打下了无比坚实的基础。因为无论后面的网络多么复杂,它们最终往往都要回到"逻辑回归"这一步,来做出那个最根本的"是"或"否"的判断。