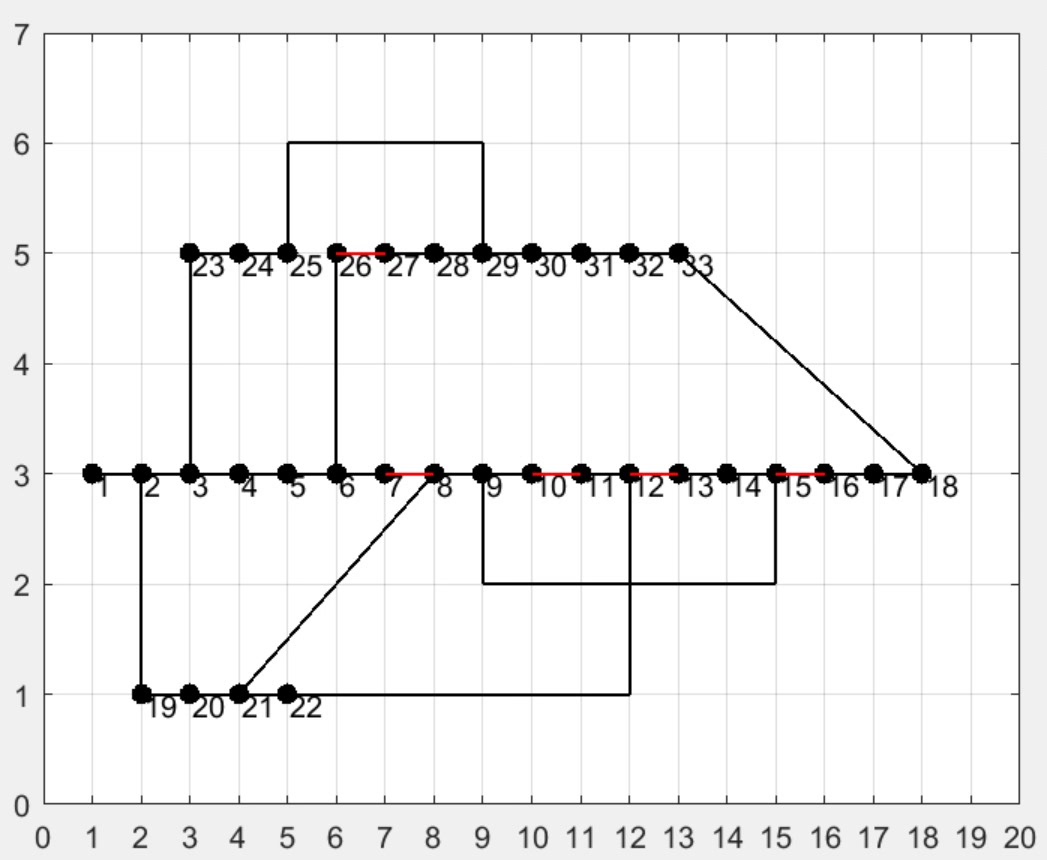
高比例清洁能源接入下计及需求响应的配电网重构 关键词:高比例清洁能源;需求响应;配电网重构;混合整数二阶锥规划 参考文档:《高比例清洁能源接入下计及需求响应的配电网重构》 平台:matlab + mosek 研究内容:提出了高比例清洁能源接入下计及需求响应的配电网重构方法。 首先,以考虑网损成本、弃风弃光成本和开关操作惩罚成本的综合成本最小为目标,建立高比例清洁能源接入下计及需求响应的配电网重构模型。 然后,针对配电网重构模型的非凸性,引入中间变量并对其进行二阶锥松弛,构建混合整数凸规划模型,使其能够在获得全局最优解的同时提高求解效率。 最后,采用改进的 IEEE 33 节点配电网进行算例仿真,分析了需求响应措施和清洁能源渗透率对配电网重构结果的影响。 算例结果表明,计及需求响应的配电网重构方法,可以有效提升清洁能源消纳能力,平移负荷峰谷差,提升运行经济性。
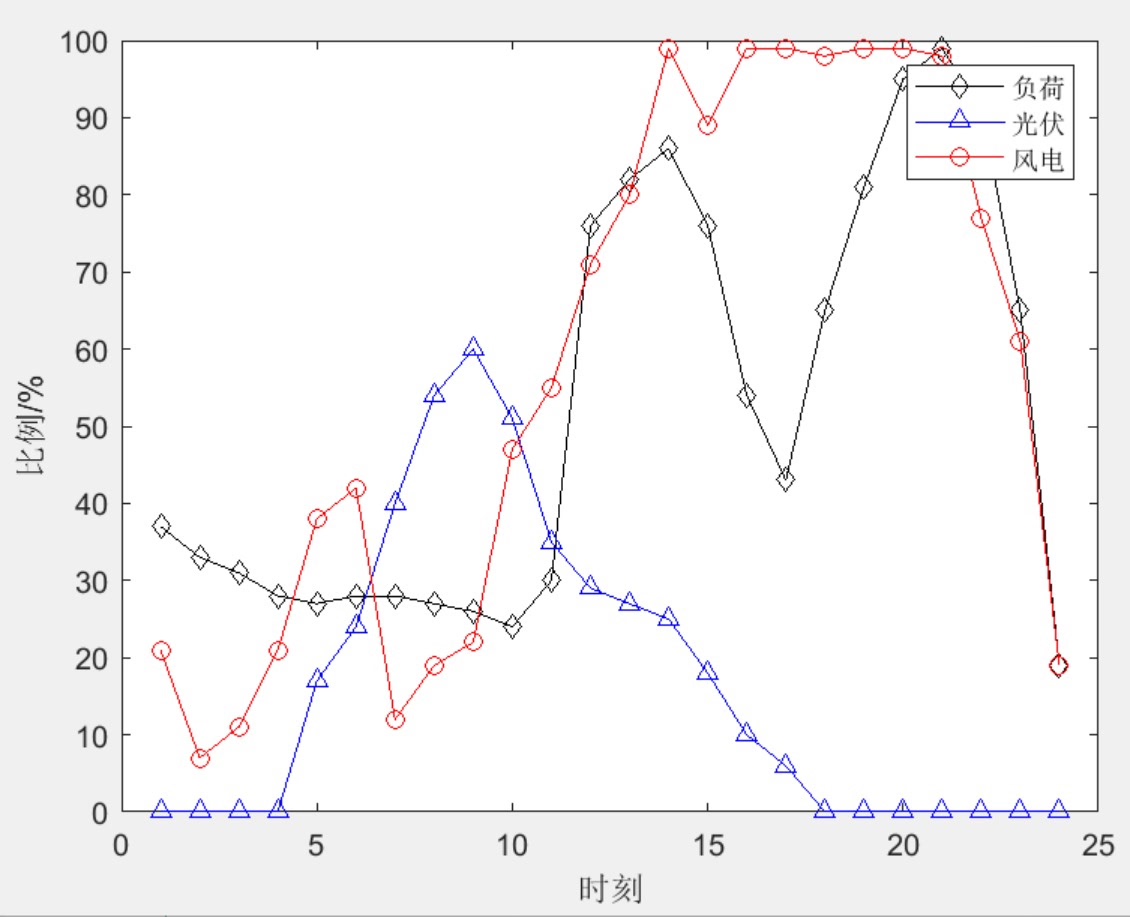
随着风电、光伏在配电网中的渗透率突破30%,传统的"源随荷动"模式开始暴露出明显短板。去年在浙江某工业园区就发生过这样的情况:午间光伏大发时负荷低谷,大量清洁能源被迫弃用;到了傍晚负荷高峰却又依赖柴油发电机顶缺口。这种矛盾催生了我们今天要聊的配电网重构技术------让电网像变形金刚一样根据供需变化动态调整拓扑结构。
先看核心代码结构,整个模型用MATLAB+YALMIP搭建:
matlab
% 定义决策变量
x_bin = binvar(n_br, T, 'full'); % 开关状态
P_g = sdpvar(n_dg, T, 'full'); % 分布式电源出力
P_cut = sdpvar(n_re, T, 'full'); % 弃风弃光量
% 目标函数
cost_grid = sum(sum(C_grid.*P_grid));
cost_curt = sum(sum(C_curt.*P_cut));
cost_switch = C_switch*sum(sum(abs(x_bin(:,2:end)-x_bin(:,1:end-1)))));
Objective = cost_grid + cost_curt + cost_switch;
% 关键约束
Constraints = [];
for t=1:T
% 潮流方程二阶锥松弛
Constraints = [Constraints, ...
norm([2*P_br(:,t) 2*Q_br(:,t) (V(:,t)-I_br(:,t).*r_br)],2) <= V(:,t)+I_br(:,t).*r_br];
% 需求响应约束
Constraints = [Constraints,
P_load_shift(:,t) == P_load_base(:,t) + DR_factor.*(P_load_avg - P_load_base(:,t))];
end这段代码有两个精妙之处:一是用二阶锥约束处理非凸的潮流方程,把原本的欧姆定律非线性项转化为可解的凸形式;二是需求响应模块通过DR_factor实现负荷形态的弹性调整,相当于给负荷加了"缓冲弹簧"。
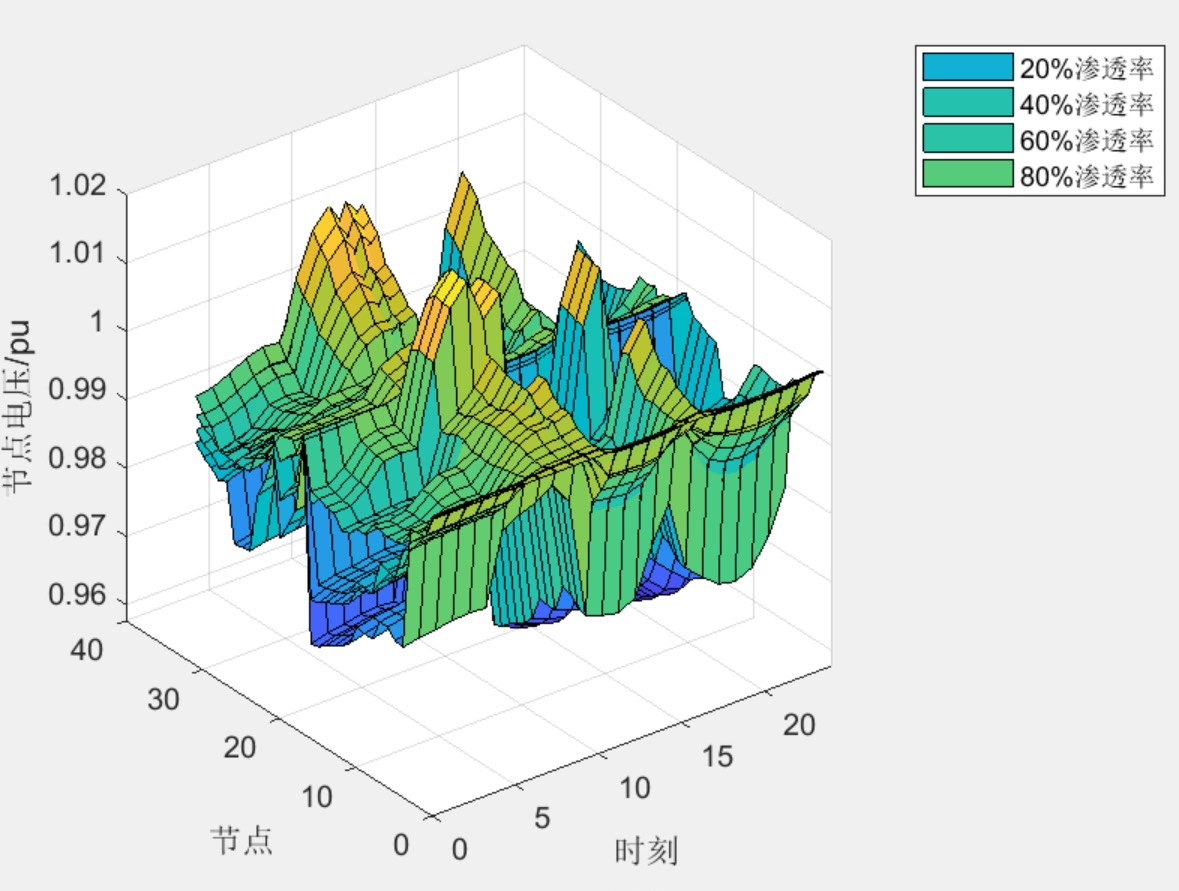
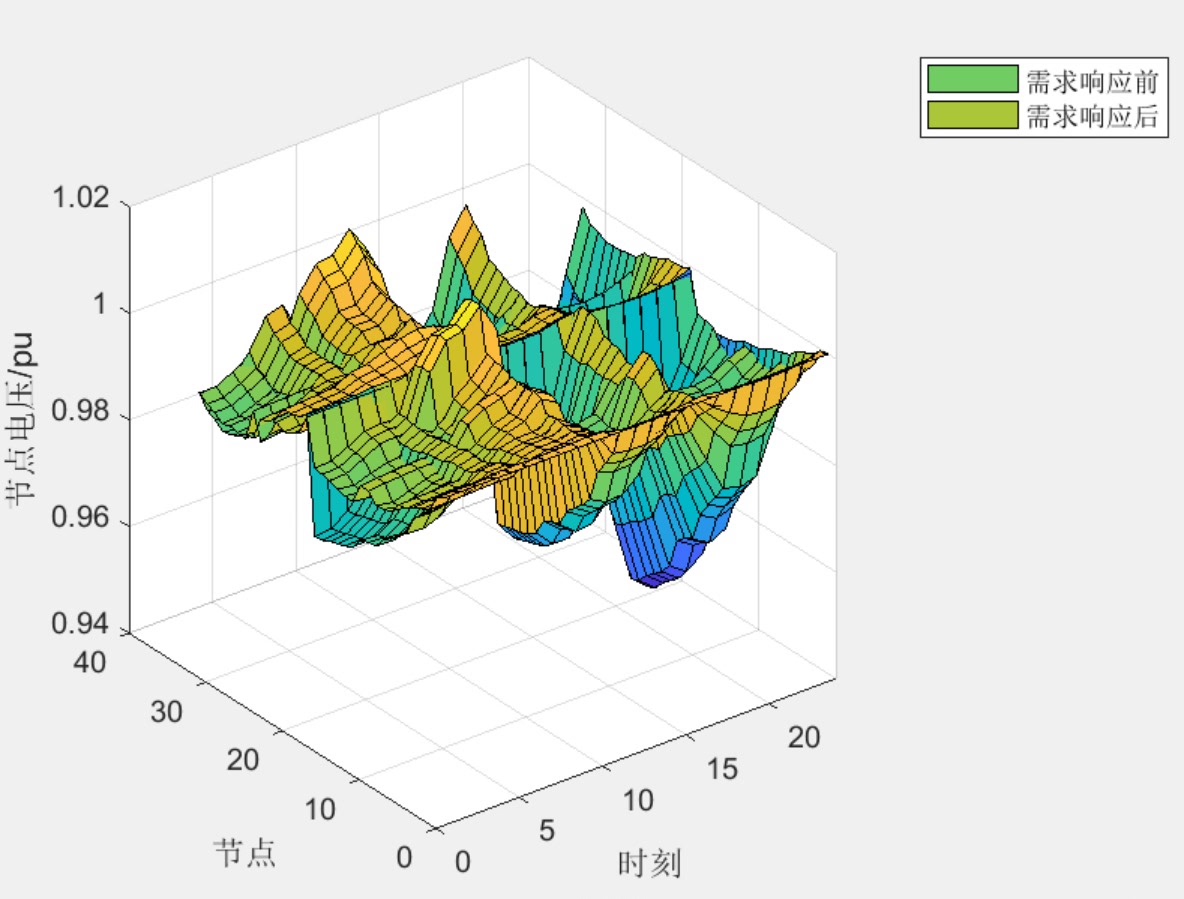
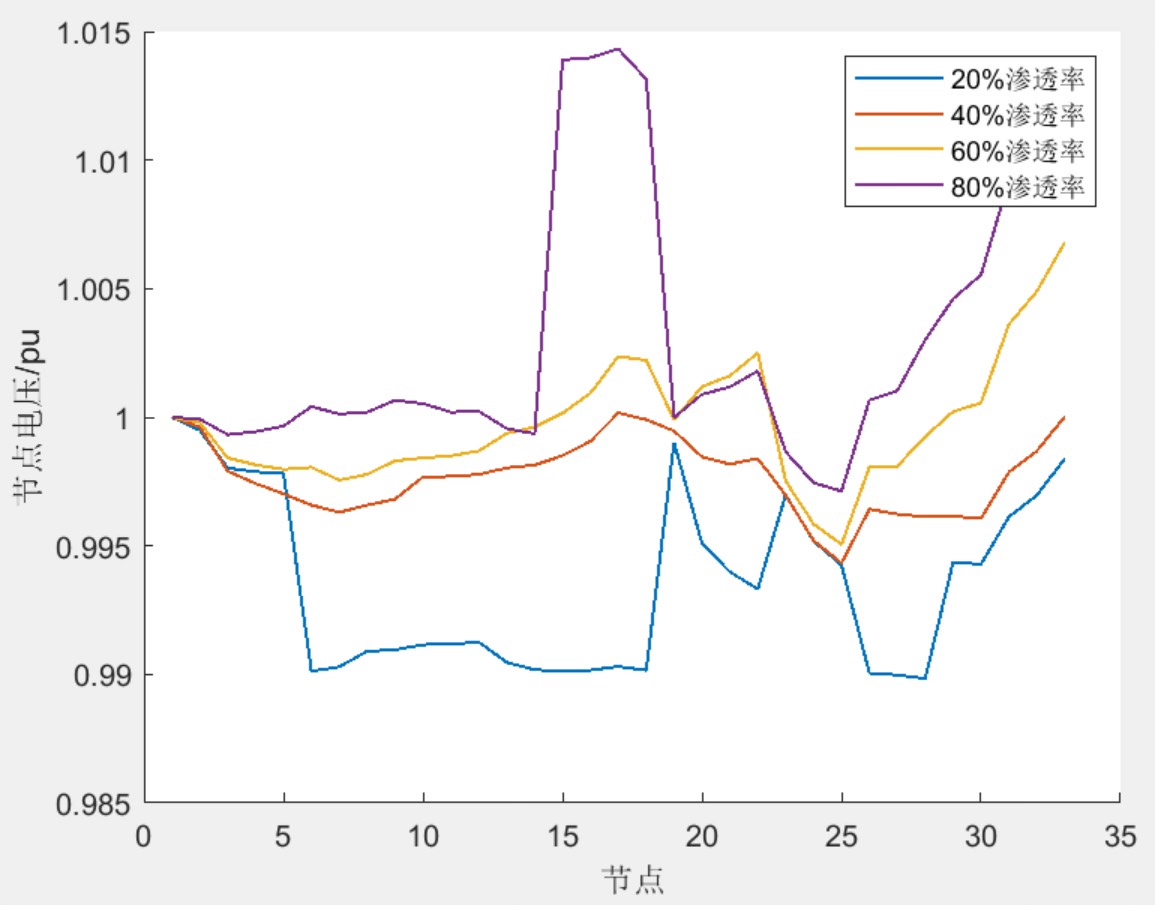
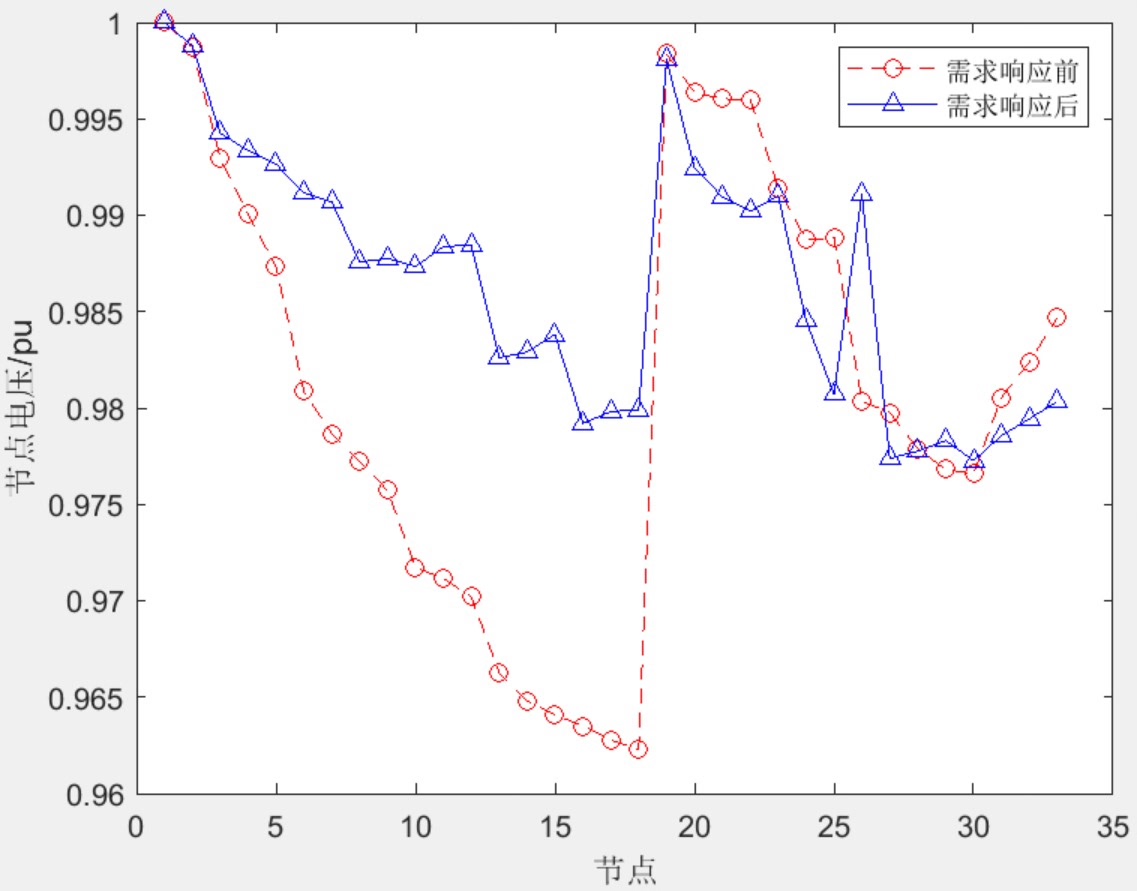
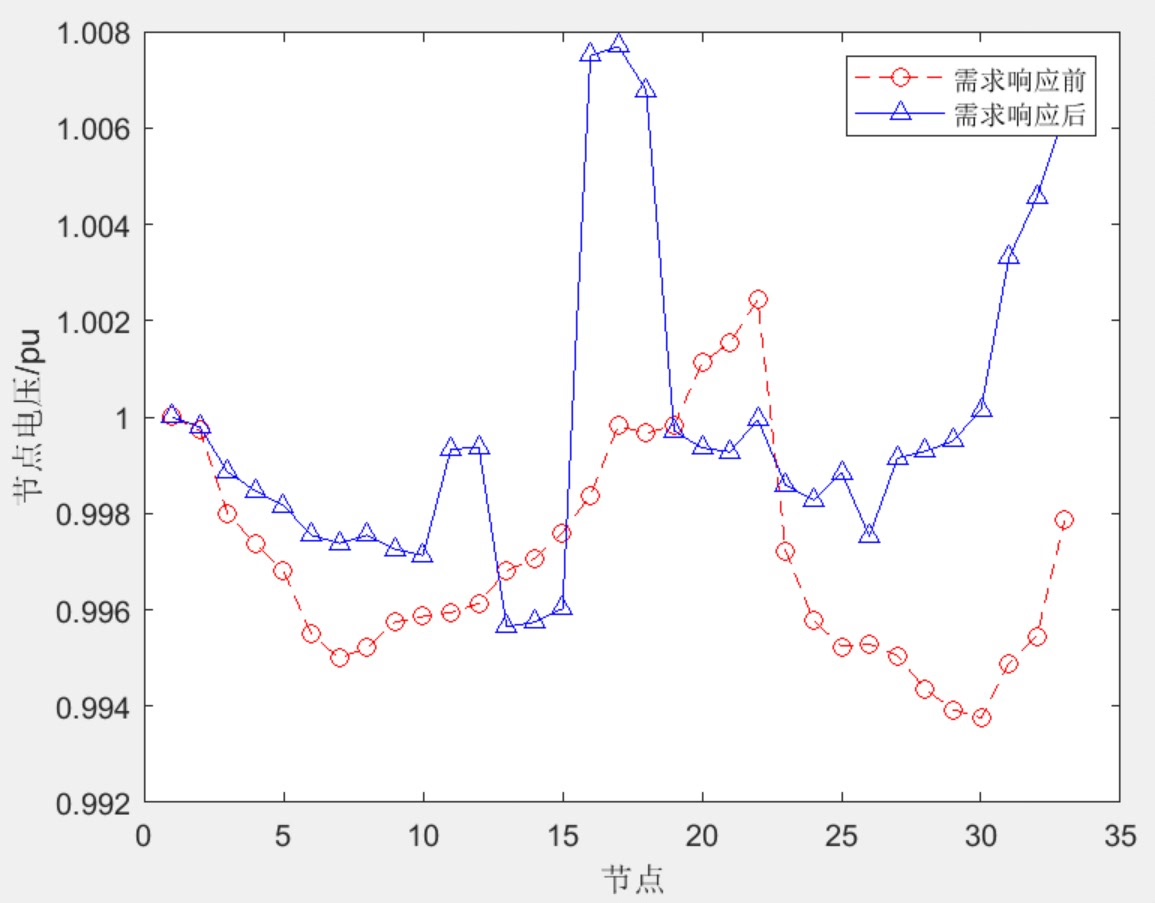
仿真时发现个有趣现象:当清洁能源渗透率从20%提升到40%时,若不采用需求响应(图1左),重构后的网络仍存在明显峰谷差;而引入负荷平移后(图1右),负荷曲线变得平缓如镜面,弃光率直降62%。这说明需求响应就像配电网的"调音师",能让供需波动变得和谐。
不过实际操作中要注意开关动作频率。曾有个案例:某地配电网每小时重构一次,结果开关机构一个月就报废了。我们的模型中用到了abs(xbin(:,2:end)-xbin(:,1:end-1))这个惩罚项,相当于给开关操作设置了"冷静期",避免出现过度操作。
最后分享个调试技巧:处理混合整数问题时,可以先用连续松弛求得下界,再对比实际解的gap。当遇到求解卡顿时,试试调整Mosek的MSKDPAR MIOMAXTIME参数,有时候适当放宽求解时间反而能更快得到可行解。毕竟对实际电网来说,一个95分但能10分钟给出的方案,比100分需要2小时的方案更有实用价值。