前言
二分算法是细节最多,最容易写出死循环的算法,但熟练后也是最简单的
二分查找不止可以运用在数组有序的情况下,在数组无序时,满足"二段性"依旧可以引用
此章开始引入模板,但关于模板一定要理解之后记忆而不是死记硬背
模板:
1.朴素的二分查找
2.查找左边界的二分模板
3.查找右边界的二分模板
目录
1.二分查找
https://leetcode.cn/problems/binary-search/

理解题意
对升序有序整型数组给定目标值,存在即返回下标,否则返回-1

算法原理
解法一:暴力解法,O(N)
直接遍历,存在即返回
解法二:二分查找
不论数组是否有序,都可以随意选取一个元素,将其与目标值对比,之后再次进行范围的增加或者减小,其本质是数组有"二段性"
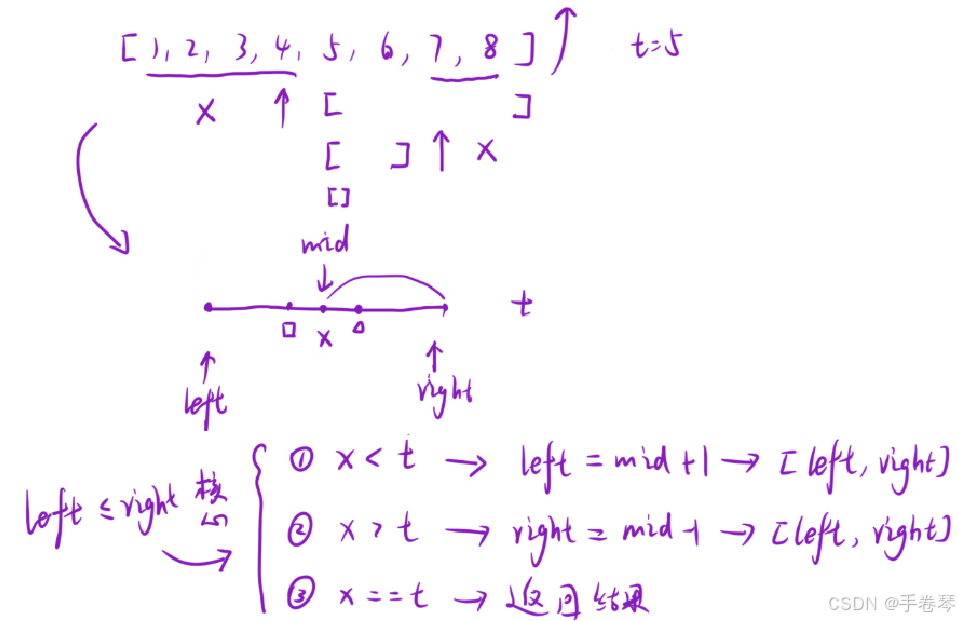
细节问题
1.当left > right时,循环结束
2.时间复杂度:
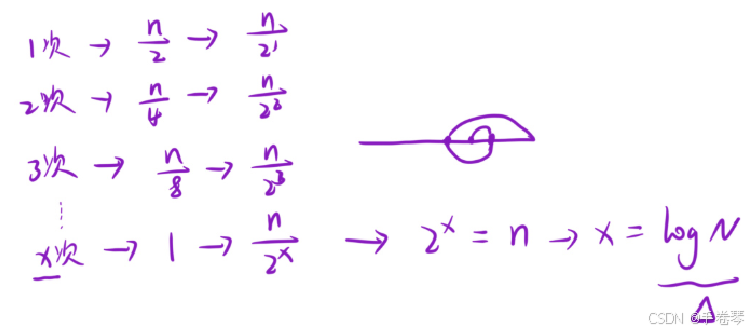
logN的时间复杂度会有多块呢? 2^32 在O(N)下 4 * 10^9,但在O(logN)下只需要32次
扩展
一般进行二分查找的划分是在中间位置进行划分,但为什么?
这与概率学的数学期望有关,从中间位置开始,其时间复杂度是最好的
本题做法
1.定义left,right,mid
2.求mid尽量不要这样写:mid = (left + right) / 2; 而是mid = left + (right - left) / 2; 或者mid = (left + right + 1) / 2;或者mid = left + (right - left + 1) / 2; 可以防止溢出
代码
暴力解法:
class Solution {
public:
int search(vector<int>& nums, int target) {
int sub = 0;
for (auto i : nums) {
if (target == i) {
return sub;
}
sub++;
}
return -1;
}
};二分解法:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while(left <= right)
{
int mid = left + (right - left) / 2; // 防止溢出
if(nums[mid] < target)
{
left = mid + 1;
}
else if(nums[mid] > target)
{
right = mid - 1;
}
else
return mid;
}
return -1;
}
};朴素二分模板
while(left <= right)
{
int mid = left + (right - left) / 2;
if(......)
{
left = mid + 1;
}
else if(......)
{
right = mid - 1;
}
else
return ......;
}注意:一定要是left <= right
求mid尽量不要这样写:mid = (left + right) / 2; 而是mid = left + (right - left) / 2; 或者mid = left + (right - left + 1) / 2; 可以防止溢出
对于式中是否+1,都不会影响最终判断结果:
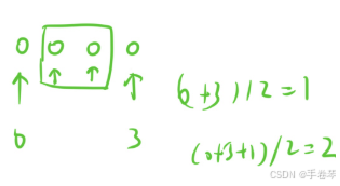
2.在排序数组中查找元素的第一个和最后一个位置
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

理解题意
1.非递减:不动或者递增

2.返回目标值最前和最后的位置下标
题目示例

算法原理
解法一:暴力解法,O(N)
定义begin和end,依次查找整个数组
解法二:朴素二分
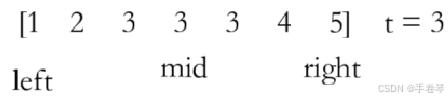
当mid直接指向目标值时,要想判断mid指向的是起始值还是结束值又或者中间值,还需要将mid向前和向后遍历查看所在位置,此时效率和暴力查找一样(将上述数组全换为3)
解法三:左右边界查找
依旧根据二段性判断
1.查找区间的左端点
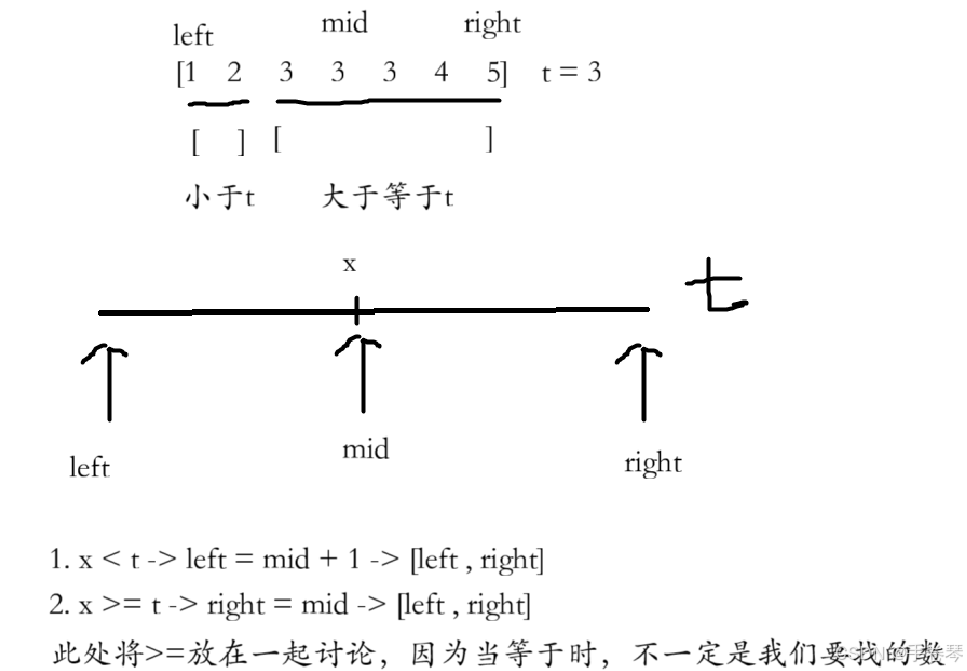
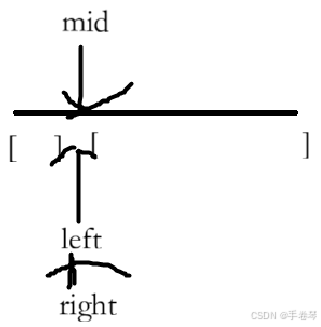
细节处理
1.循环条件应该是left < right,而不是left <= right
第一种情况:有结果
当mid == right == left时,就是最终结果,因此不必判断
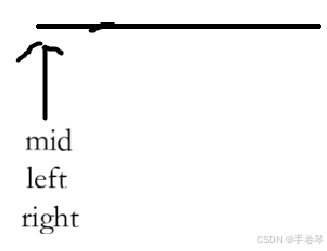
第二种情况:全大于t
仅仅只需要判断mid的值即可
第三种情况:全小于t
情况与第二种相似
总结此细节:当left == right时就是最终结果,如果判断,就会进入死循环。
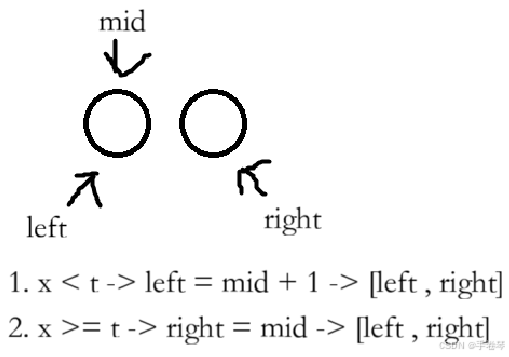
2.求中点操作
利用"二段性"
在朴素二分中,防止溢出有:mid = left + (right - left) / 2; (命中左端点)或者mid = left + (right - left + 1) / 2;(命中右端点) 两种操作。
但在此时只能使用mid = left + (right - left) / 2;
当使用mid = left + (right - left + 1) / 2;时:
如果此刻mid满足第二种形式,right会在原地不动,然后接着判断,从而陷入死循环。
2.查找区间右端点
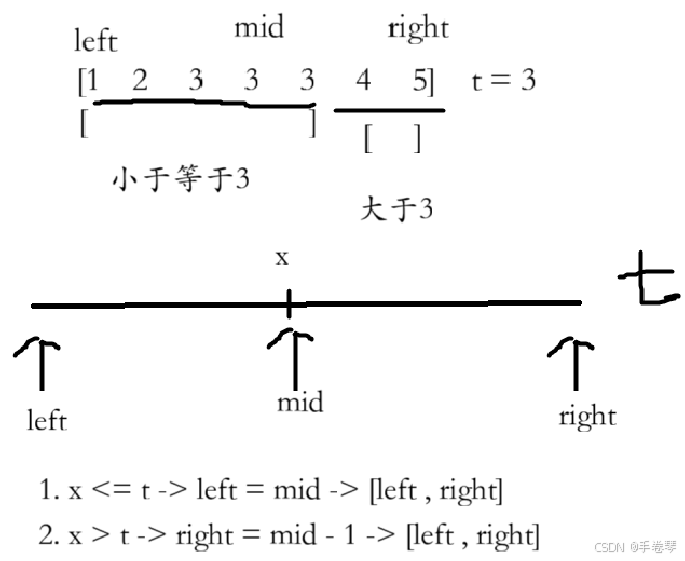
1.循环条件应该是left < right,而不是left <= right
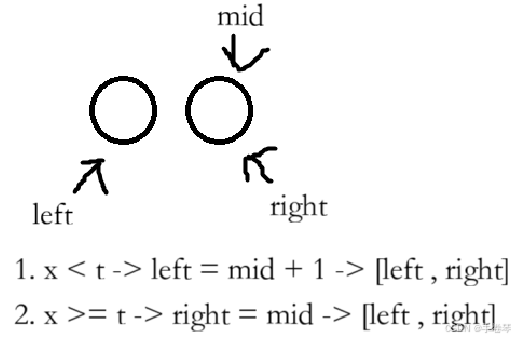
2.求中点方式
在朴素二分中,防止溢出有:mid = left + (right - left) / 2; (命中左端点)或者mid = left + (right - left + 1) / 2;(命中右端点) 两种操作。
但在此时只能使用mid = left + (right - left + 1) / 2;
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
// 边界情况
if(nums.size() == 0)
return {-1,-1};
int begin = 0;
// 二分左端点
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target)
left = mid + 1;
else right = mid;
}
// 判断是否有结果
if(nums[left] != target)
return {-1,-1};
else begin = left;
// 二分右端点
left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target)
left = mid;
else right = mid - 1;
}
return {begin,right};
}
};左右端点模板
// 二分左端点
while(left < right)
{
int mid = left + (right - left) / 2;
if(......)
left = mid + 1;
else
right = mid;
}
// 二分右端点
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(......)
left = mid;
else
right = mid - 1;
}本章节持续更新。