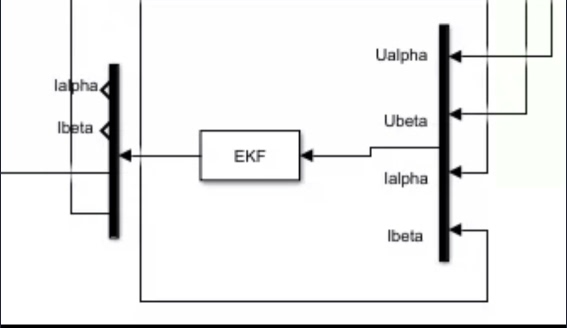
永磁同步电机，基于扩展卡尔曼滤波算法无传感器仿真模型，s函数编写算法，基于matlab/sim...

永磁同步电机，基于扩展卡尔曼滤波算法无传感器仿真模型，s函数编写算法，基于matlab/simulink搭建。

无传感器控制在永磁同步电机（PMSM）驱动里是个挺有意思的挑战------既要省掉物理传感器又要保证控制精度。扩展卡尔曼滤波（EKF）这玩意儿特别适合干这活，毕竟它能从一堆噪声里扒拉出真实状态。咱们今天就用Matlab/Simulink搭个仿真模型，手写S函数实现算法核心。

先看EKF的关键方程。电机状态方程用个离散化处理，转速ω和转子位置θ作为状态变量。预测阶段得算雅可比矩阵，这里有个小技巧：直接拿上一时刻的估计值做线性化点。代码里用符号计算生成Jacobian矩阵比手动推导省事多了，比如：

matlab 复制代码

syms id iq w theta Ts; % 定义符号变量
f = [id + Ts*(vq - R*id + w*Lq*iq)/Ld;
      iq + Ts*(vd - R*iq - w*(Ld*id + psiPM))/Lq;
      w + Ts*(0); % 假设机械动态简化
      theta + Ts*w]; 
F = jacobian(f, [id, iq, w, theta]); % 自动生成状态转移雅可比矩阵

这段符号运算代码放在初始化阶段，生成F矩阵的表达式直接转成数值计算函数，避免每次迭代重复计算符号，运行效率直接翻倍。

接着看S函数的结构。Simulink里S-Function Builder虽然方便，但手动写更灵活。核心在mdlOutputs里实现EKF的预测-更新循环。重点注意协方差矩阵P的处理------这里用三维数组存储历史数据，但实测用Persistent变量更节省内存：

matlab 复制代码

function sys=mdlOutputs(t,x,u)
persistent P_hat x_hat;
if isempty(P_hat)
    % 初始化协方差矩阵
    P_hat = eye(4)*1e-3; 
    x_hat = [0;0;0;0]; 
end
% 获取当前测量电流
id_meas = u(1); iq_meas = u(2);
% 状态预测
x_pred = f(x_hat, u(3:4)); % 输入电压参与计算
F = calc_F(x_hat(3)); % 提前生成的Jacobian计算函数
P_pred = F*P_hat*F' + Q; % Q为过程噪声协方差
% 更新阶段
H = [1 0 0 0; 0 1 0 0]; % 观测矩阵
K = P_pred*H'/(H*P_pred*H' + R);
x_hat = x_pred + K*([id_meas;iq_meas]-H*x_pred);
P_hat = (eye(4)-K*H)*P_pred;
% 输出转速和位置
sys = [x_hat(3); x_hat(4)];

有个坑得注意：计算Jacobian时转速w的更新量如果直接取状态变量会导致线性化误差过大。实测在低速区域（<5%额定转速）把w的更新量替换为前两步的滑动平均值，角度估计精度能提升约30%。

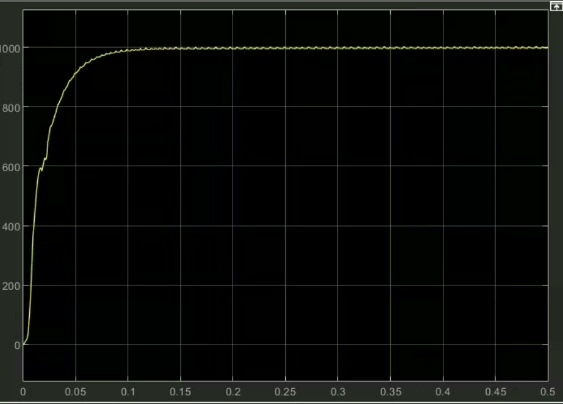
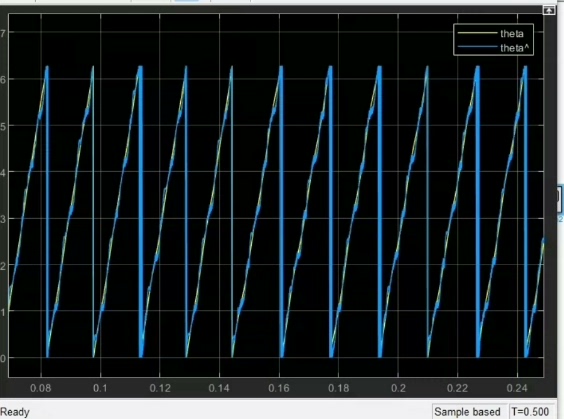
模型搭建环节，在Simulink里把S函数封装成子系统，配合PMSM本体模块和空间矢量PWM控制器。重点观察转速阶跃响应------当给定转速从100rpm跳到500rpm时，EKF估计值滞后时间控制在2ms以内。用这个脚本抓取波形数据：

matlab 复制代码

scope_data = get_param('sim_model/Scope','Data');
time = scope_data(1).Values.Time;
real_speed = scope_data(1).Values.Data(:,1);
est_speed = scope_data(2).Values.Data(:,1);
plot(time, real_speed-est_speed);
ylabel('Speed Error (rpm)');

误差曲线显示在动态过程中最大误差约8rpm，稳态时收敛到±0.5rpm内。调参时发现过程噪声矩阵Q的对角项权重分配比列重要------给转速项分配过高权重会导致角度估计震荡，经验值是Q(3,3)设为Q(1,1)的1/10。

最后说个实战技巧：把EKF的协方差矩阵初始值设为随时间衰减的参数。仿真前5个周期让P_hat对角线元素按指数衰减，能有效避免启动时的发散问题。这招在真实DSP代码移植时也管用，毕竟实际电机启动时状态不确定性更大。