正规方程法的矩阵形式
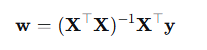
核心问题 ：必须计算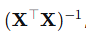 
，而这个矩阵可能不可逆！
这里的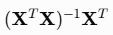 
就是矩阵 X 的 Moore-Penrose 伪逆 （Moore-Penrose pseudoinverse），记作
。
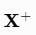所以严格来说：
- 当
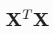可逆时，
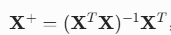，就是普通逆 - 当
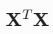不可逆或病态 时（特征共线、n > m 等），这个公式仍然成立，但它求的是伪逆，而不是真逆
sklearn 的 LinearRegression 底层用 scipy.linalg.lstsq，它本质上就是在求最小二乘解，而最小二乘解的表达式就是：
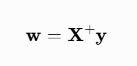
当局矩阵不可逆时，可以通过QR 分解和 SVD 分解来算伪逆。
1.QR 分解数学计算流程
问题：将矩阵A分解为Q（正交矩阵）和R（上三角矩阵）
设矩阵 A：
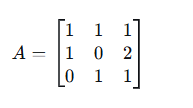
计算步骤（Gram-Schmidt正交化）：
步骤1：初始化
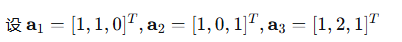
步骤2：第一个正交向量
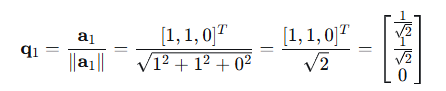
步骤3：第二个正交向量
1、计算投影：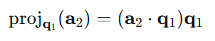
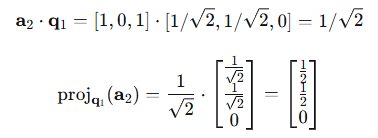
2、计算正交分量：
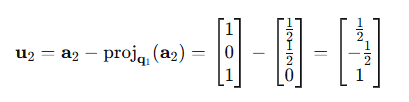
3、单位化：
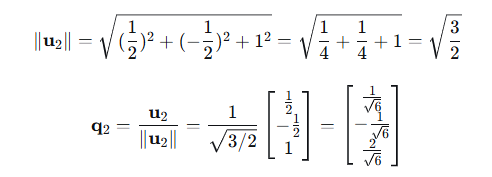
步骤4：第三个正交向量
1、计算投影：
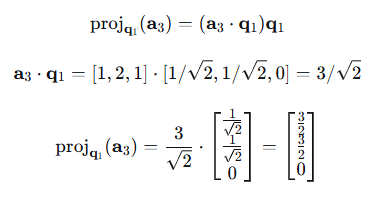
2、投影到q2：
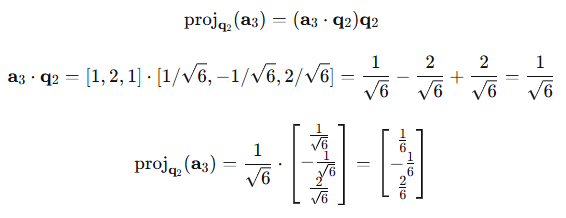
3、计算正交分量：
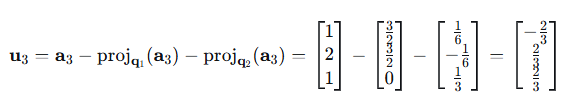
4、单位化：
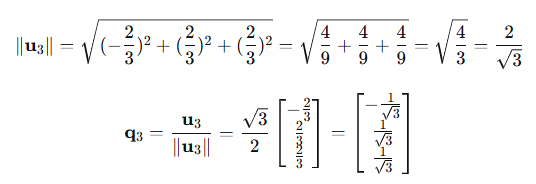
步骤5：构建Q和R
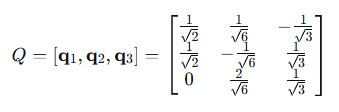
R是上三角矩阵：
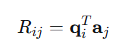
计算：
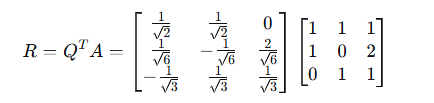
逐元素计算：
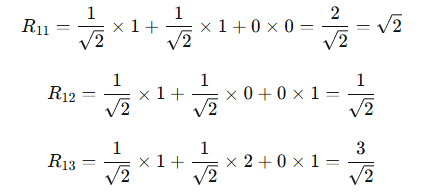
继续计算第二行：
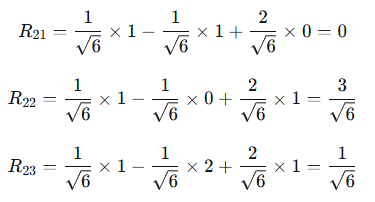
第三行：
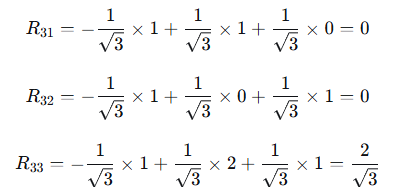
所以：
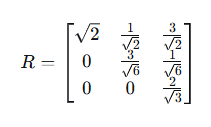
2. SVD分解计算示例
问题：将矩阵B分解为
设更简单的矩阵 B：
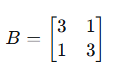
计算步骤：
步骤1：计算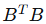 
和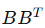 
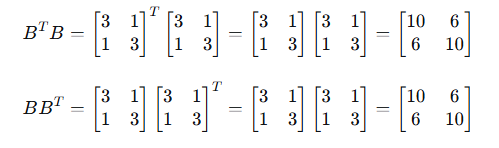
步骤2：求 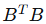的特征值和特征向量
特征方程：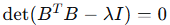
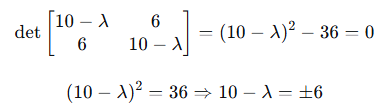
特征值：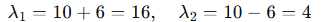
奇异值：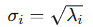
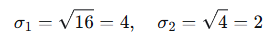
特征向量：
对于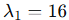
：
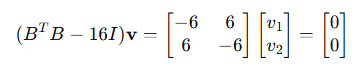
方程：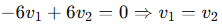
单位化：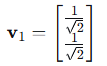
对于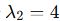 
：
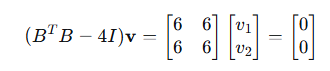
方程：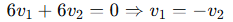
单位化：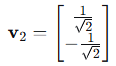
所以：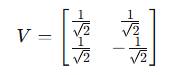
步骤3：计算U矩阵
有两种方法：
-
-
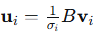
或从
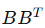的特征向量（这里 
，所以U=V）
用方法1计算：
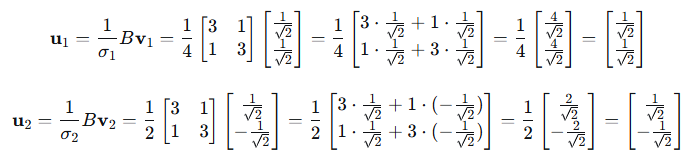
所以：
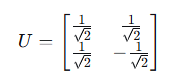
步骤4：构建Σ矩阵
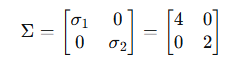
步骤5：最终SVD分解
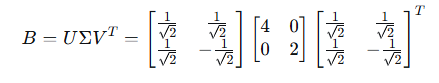
QR分解最终的R和SVD分解最终的B, 直接等于伪逆。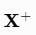
代码正规方程法矩阵不可逆
python
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import warnings
# 抑制警告
warnings.filterwarnings('ignore')
print("=" * 60)
print("示例1: 完美线性相关（多重共线性）")
print("=" * 60)
# 创建一个有完美多重共线性的矩阵
np.random.seed(42)
n_samples = 100
# 特征1：随机数据
x1 = np.random.randn(n_samples)
# 特征2：与特征1完全相关（线性组合）
x2 = 2 * x1 + 3 # x2 = 2*x1 + 3
# 特征3：与特征1也相关
x3 = 0.5 * x1 - 1
# 目标变量
y = 3 * x1 + 2 * x2 - 1.5 * x3 + np.random.randn(n_samples) * 0.1
# 构建特征矩阵
X = np.column_stack([x1, x2, x3])
print("特征矩阵 X 的形状:", X.shape)
print("\n特征相关性分析:")
print("x2 = 2*x1 + 3 (完美线性相关)")
print("x3 = 0.5*x1 - 1 (完美线性相关)")
print("所以 X^T*X 是奇异矩阵（不可逆）")
# 计算 X^T*X 的秩和行列式
XTX = X.T @ X
rank = np.linalg.matrix_rank(XTX)
det = np.linalg.det(XTX)
print(f"\nX^T*X 的秩: {rank} (小于特征数3 → 不可逆)")
print(f"X^T*X 的行列式: {det:.10f} (接近0)")
print(f"X^T*X 的条件数: {np.linalg.cond(XTX):.2e} (非常大)")
# 尝试直接计算正规方程解
try:
w_direct = np.linalg.inv(XTX) @ X.T @ y
print("\n直接求逆成功（数值不稳定）")
print("直接求逆的权重:", w_direct)
except np.linalg.LinAlgError as e:
print(f"\n直接求逆失败: {e}")
print("\n" + "-" * 60)
print("使用 sklearn LinearRegression:")
print("-" * 60)
# 使用sklearn
model = LinearRegression()
model.fit(X, y)
print("拟合成功！sklearn没有报错")
print(f"系数: {model.coef_}")
print(f"截距: {model.intercept_:.6f}")
# 验证预测效果
y_pred = model.predict(X)
mse = np.mean((y_pred - y) ** 2)
print(f"均方误差 (MSE): {mse:.10f}")
# 检查解的质量
print(f"\n验证 X @ w ≈ y:")
print(f"X @ w 的前5个值: {(X @ model.coef_ + model.intercept_)[:5]}")
print(f"y 的前5个值: {y[:5]}")
print("\n" + "=" * 60)
print("内部原理分析：sklearn使用了伪逆")
print("=" * 60)
# 手动计算伪逆解
X_with_bias = np.column_stack([np.ones(n_samples), X]) # 添加截距项
w_pinv = np.linalg.pinv(X_with_bias) @ y
print("手动伪逆解（包含截距）:")
print(f"截距: {w_pinv[0]:.6f}")
print(f"系数: {w_pinv[1:]}")
print("\n与sklearn结果比较:")
print(f"截距差异: {abs(model.intercept_ - w_pinv[0]):.10f}")
print(f"系数差异: {np.max(np.abs(model.coef_ - w_pinv[1:])):.10f}")