（数据结构）二叉树、二叉搜索树+简单的排序算法（考前速成版）

404未精通的狗2025-12-21 8:38

二叉树、二叉搜索树+简单排序算法

此笔记为博主机考前抱佛脚所做，不管有没有用也一并上传记录下来罢，由于时间仓促笔记基本做在了代码注释中
以及特别鸣谢以下视频带我抱佛脚：

  1. 考研数据结构代码完整带你敲一遍！！！带运行！！！从新建一个文件开始！！！
  2. 二叉搜索树的删除操作
  3. 【有挂！！】二叉树遍历秒解，前序遍历、中序遍历、后序遍历

二叉树

实现：

  1. 初始化
  2. 清空树
  3. 按给定元素顺序插入树
  4. 查找树的值为x的结点
  5. 求树的高度
  6. 输出二叉树（前、中、后序遍历、层序遍历）
  7. 判树空
c 复制代码 
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

//二叉树
typedef struct treeNode {
	int val;
	struct treeNode* lchild,*rchild;
}BTNode;

typedef struct {
	int num;//计算树的结点，可以判断是否是空树
	BTNode* root;//树的根节点
}BTree;

//初始化二叉树
BTree* initBTree() {
	BTree* btree = (BTree*)malloc(sizeof(BTree));
	btree->num = 0;
	btree->root=NULL;
	return btree;
}

//清空树
//拆解成先清空孩子结点、再清空根节点的小任务
void clearAssist(BTNode* root,int* num ) {
	if (!root) return;
	clearAssist(root->lchild, num);
	clearAssist(root->rchild, num);
	(*num)--;
	free(root);
}
bool clearBTree(BTree* t) {
	if (!t || t->num == 0) return true;
	clearAssist(t->root, &t->num);
	// 清空后根节点置空（避免悬空指针）
	t->root = NULL;
	return true;
}

//查找结点（同样使用递归）
BTNode* searchAssist(BTNode* root, int x) {
	if (!root) return NULL;
	if (root->val == x) return root;
	BTNode* left = searchAssist(root->lchild, x); 
	BTNode* right= searchAssist(root->rchild, x);
	// 优先返回左子树的结果：左找到则返回左，否则返回右，都没找到返回NULL
	return left ? left : right;
}

BTNode* searchXBTree(BTree* t, int x) {
	if (!t||t->num==0) return NULL;
	return searchAssist(t->root,x);
}

//求树的高度，依然使用递归，从底下往上数，左右分开数取大的
//依然是清楚：退出条件、重复部分和返回值
int heightAssist(BTNode* root) {
	if (!root) return 0;
	int left=heightAssist(root->lchild);
	int right=heightAssist(root->rchild);
	return left > right ? left + 1 : right + 1;
}
int getHBTree(BTree* t) {
	if (!t || t->num == 0) return 0;
	return heightAssist(t->root);
}
//判断树空
bool isEmptyBTree(BTree* t) {
	if (!t || t->num == 0) return true;
	else return false;
}

//按给定的元素插入树 arr[5]={1,2,3,4,5}
//层序遍历思想：把结点赋值后放入队列，每次取出头结点并把其左右子节点入队
//层序遍历就在取队头时输出元素

BTree* insertArrBTree(BTree* btree, int* arr,int n)//n是arr中元素数
{
	if (!btree) return NULL;
	if (btree->num == 0) {
		btree->root = (BTNode*)malloc(sizeof(BTNode));
		btree->root->lchild = btree->root->rchild = NULL;
		//把头结点先按照arr赋值
		btree->root->val = arr[0];
		btree->num++;
	}
	//创建队列,注意存储的是结点的指针
	BTNode* queue[1000] = { 0 };
	//先把根节点入队
	queue[0] = btree->root;
	//队尾入列，队头出列
	int in = 1, out = 0;
	int i = 1;
	while (i < n) {
		//先取出队列的头节点,注意对out处理
		BTNode* cur = queue[out++];
		//如果左节点非空（赋过值了），直接入队.注意队列操作时对in、out的处理
		if (cur->lchild) {
			queue[in++] = cur->lchild;
		}
		//如果是空的要先赋值(注意包括需要开辟空间、给孩子置空、再赋值）
		else {
			cur->lchild = (BTNode*)malloc(sizeof(BTNode));
			cur->lchild->lchild = cur->lchild->rchild = NULL;
			cur->lchild->val = arr[i++];
			queue[in++] = cur->lchild;
			btree->num++; 
		}
		if (i >= n) break;//如果此时已经加完元素了，就退出
		//接着看右孩子
		if (cur->rchild) {
			queue[in++] = cur->rchild;
		}
		//如果是空的要先赋值(注意包括需要开辟空间、给孩子置空、再赋值）
		else {
			cur->rchild = (BTNode*)malloc(sizeof(BTNode));
			cur->rchild->lchild = cur->rchild->rchild = NULL;
			cur->rchild->val = arr[i++];
			queue[in++] = cur->rchild;
			btree->num++;
		}
	}
	return btree;
}

//输出二叉树-前、中、后、层序遍历
//前中后都利用递归
void preAssist(BTNode* root) 
{
	if (!root) return;
	printf("%d ", root->val);//根
	preAssist(root->lchild);//左
	preAssist(root->rchild);//右
}
void preShowBTree(BTree* btree)
{
	if (!btree) return;
	preAssist(btree->root);
}

void midAssist(BTNode* root)
{
	if (!root) return;
	midAssist(root->lchild);//左
	printf("%d ", root->val);//根
	midAssist(root->rchild);//右
}
void midShowBTree(BTree* btree)
{
	if (!btree) return;
	midAssist(btree->root);
}

void behAssist(BTNode* root)
{
	if (!root) return;
	behAssist(root->lchild);//左
	behAssist(root->rchild);//右
	printf("%d ", root->val);//根
}
void behShowBTree(BTree* btree)
{
	if (!btree) return;
	behAssist(btree->root);
}

//层序遍历
void leverShowBTree(BTree* btree) {
	if (!btree) return;
	BTNode* queue[1000] = {NULL};
	queue[0] = btree->root;
	int in = 1, out = 0;
	int i = 0;
	//循环的条件是队列非空
	while (out!=in) {
		BTNode* cur = queue[out++];
		printf("%d ", cur->val);
		if (cur->lchild) queue[in++] = cur->lchild;
		if (cur->rchild) queue[in++] = cur->rchild;
	}
	printf("\n");
}

int main()
{
	BTree* t = initBTree();
	int arr[10] = { 3,1,2,5,4,6,7,11,9,5 };
	insertArrBTree(t, arr, 10);
	preShowBTree(t);
	printf("\n");
	leverShowBTree(t);
	printf("%d \n", t->num);
	clearBTree(t);
	printf("%d \n", t->num);
	return 0;
}

二叉搜索树

实现：

  1. 插入值为x的结点
  2. 按给定数组创建树
  3. 查找值为x的结点：利用二叉搜索树的特点
  4. 删除值为x的结点（第一个遇到的）
  5. 查询元素个数（递归）------二叉树通用
c 复制代码 
#include <stdio.h>
#include <stdlib.h>

//二叉搜索树，主要的功能是查找（相同元素可以不放进树）
//对3、1、2、5、4使用一定的规则插入，保证对每个根结点，比他小于等于的在左边，比他大的在右边



//结点------直接用二叉树的结点就行
typedef struct BTNode {
	struct BTNode* lchild;
	struct BTNode* rchild;
	int val;
}BTNode;
typedef struct {
	int num;//计算树的结点，可以判断是否是空树
	BTNode* root;//树的根节点
}BTree;

//1. 插入值为x的结点
BTNode* insertBST(BTNode* root,int x) {
	BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
	cur->lchild = cur->rchild = 0;
	cur->val = x;
	BTNode* in = root;//插入结点当前的父节点，初始化
	//循环找cur的插入位置
	while (1) {
		//如果cur比in小或等于，放左边
		if (cur->val <= in->val) {
			//如果左边为空，直接插入退出循环
			if (!in->lchild) {
				in->lchild = cur;
				break;
			}
			//如果左边不为空，继续往下走
			else {
				in = in->lchild;
				continue;
			}
		}
		//如果cur比root大，放右边
		else {
			//如果右边为空，直接插入退出循环
			if (!in->rchild) {
				in->rchild = cur;
				break;
			}
			//如果右边不为空，继续往下走
			else {
				in = in->rchild;
				continue;
			}
		}
	}
	return root;
}
//2. 给定数组创建树
BTNode* createBST(int* arr, int n) {
	if (!arr || n <= 0) return NULL;//创建失败
	//1.设置arr[0]为根节点
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->lchild = root->rchild = 0;
	root->val = arr[0];
	//2.从第二个元素开始插入
	for (int i = 1;i < n;i++) {
		root = insertBST(root, arr[i]);
	}	
	return root;
}

//3. 查找值为x的结点：利用二叉搜索树的特点
//比根小的往左找、比根大的往右找
BTNode* searchXBST(BTNode* root, int x)
{
	if (!root) return NULL;
	BTNode* cur = root;
	while (cur) {
		if (x == cur->val) return cur;
		else if (x < cur->val) {
			cur = cur->lchild;
			continue;
		}
		else if (x > cur->val) {
			cur = cur->rchild;
			continue;
		}
	}
	//如果到了这里，肯定是因为没有找到
	return NULL;
}

//4. 删除值为x的结点（第一个遇到的）
// 分情况讨论：
// 1、删除叶子结点 可以直接删除
// 2、删除只有一个子结点的结点 可以直接删除再把子结点接上父结点就行
// 3、删除有两个结点的结点（即有左右子树） 用中序前继或者后继替换这个结点（可以用中序遍历来理解）

//辅助函数1：查找目标节点的父节点
BTNode* findFatherXBST(BTNode* root, BTNode* target) {
	//没有父节点的情况
	if (!root || !target || root == target) return NULL;
	BTNode* father = root;
	while (father) {
		if (father->lchild == target || father->rchild == target) return father;
		if (target->val <= father->val) {
			father = father->lchild;
		}
		else if (target->val > father->val) {
			father = father->rchild;
		}
	}
	return NULL;//未找到父节点（目标不在树中）
}

//辅助函数2：找节点的中序后继
//Successor:后继,中序后继是该节点右子树的最左侧结点
BTNode* findMidSuccessor(BTNode* node) {
	//由于找中序后继替换的场景只在有左右子树的情况下用到，所以这里默认没有右子树就是没有中序后继
	if (!node || !node->rchild) return NULL;
	BTNode* cur = node->rchild;
	while (cur->lchild) {
		cur = cur->lchild;
	}
	return cur;
}
//核心：删除值为x的结点
BTNode* deleteXBST(BTNode* root, int x) {
	//1.找到待删除节点和父节点
	BTNode* delNode= searchXBST(root, x);
	if (!delNode) return root;//找不到x直接返回原树
	BTNode* father = findFatherXBST(root, delNode);
	//2.分情况删除结点
	////（1）删除叶子结点（结点没有子结点）
	if (!delNode->lchild && !delNode->rchild) {
		if (father->lchild== delNode) {
			father->lchild = NULL;
		}
		else {
			father->rchild = NULL;
		}
		free(delNode);
	}
	////（2）删除只有一个子节点的结点
	//只有左子树
	else if (delNode->rchild == NULL) {//全无的已经在上面处理完了
		if (father == NULL) { // 待删节点是根节点
			BTNode* newRoot = delNode->lchild;
			free(delNode);
			return newRoot;
		}
		BTNode* cur = delNode->lchild;
		// 把左子树接给父节点
		if (father->lchild == delNode) {
			father->lchild = delNode->lchild;
		}
		else {
			father->rchild = delNode->lchild;
		}
		free(delNode);
	}
	//只有右子树
	else if (delNode->lchild == NULL) {//全无的已经在上面处理完了
		if (father == NULL) { // 待删节点是根节点
			BTNode* newRoot = delNode->rchild;
			free(delNode);
			return newRoot;
		}
		BTNode* cur = delNode->lchild;
		// 把右子树接给父节点
		if (father->lchild == delNode) {
			father->lchild = delNode->rchild;
		}
		else {
			father->rchild = delNode->rchild;
		}
		free(delNode);
	}
	////(3)删除有两个子节点的结点
	else {
		//找中序后继
		BTNode* successor = findMidSuccessor(delNode);
		int successorVal = successor->val; // 暂存后继值（只用知道值就可以实现替换了）
		//删除中序后继，其必是叶子或是只有一个右子节点的结点，所以可以递归调用删除函数自身，走前两种情况解决
		root = deleteXBST(root, successorVal);
		// 用后继值替换待删节点的值
		delNode->val = successorVal;
	}
	return root;
}

//5. 查询元素个数（递归）------二叉树通用
//重复小问题：一棵树的结点数=左子树结点个数+右子树结点个数+1（根节点）
int countBST(BTNode* root) {
	if (!root) return 0;
	int left = countBST(root->lchild);
	int right = countBST(root->rchild);
	return left + right + 1;
}

//前序遍历
void preAssist(BTNode* root)
{
	if (!root)  return;
	printf("%d ", root->val);//根
	preAssist(root->lchild);//左
	preAssist(root->rchild);//右
}
//中序遍历
void midAssist(BTNode* root)
{
	if (!root) return;
	midAssist(root->lchild);//左
	printf("%d ", root->val);//根
	midAssist(root->rchild);//右
}

int main() {
	int arr[] = { 3,1,2,5,4 };
	BTNode* bst = createBST(arr, 5);

	printf("初始中序遍历：");
	midAssist(bst); // 输出：1 2 3 4 5
	printf("\n");

	insertBST(bst, 9);
	printf("插入9后中序遍历：");
	midAssist(bst); // 输出：1 2 3 4 5 9
	printf("\n");

	BTNode* search = searchXBST(bst, 2);
	if (search) printf("找到节点2：get\n");

	// 测试删除场景1：删除叶子节点（9）
	bst = deleteXBST(bst, 9);
	printf("删除叶子节点9后中序遍历：");
	midAssist(bst); // 输出：1 2 3 4 5
	printf("\n");

	// 测试删除场景2：删除单孩子节点（1，只有右孩子2）
	bst = deleteXBST(bst, 1);
	printf("删除单孩子节点1后中序遍历：");
	midAssist(bst); // 输出：2 3 4 5
	printf("\n");

	// 测试删除场景3：删除双孩子节点（3，有左右子树）
	bst = deleteXBST(bst, 3);
	printf("删除双孩子节点3后中序遍历：");
	midAssist(bst); // 输出：2 4 5
	printf("\n");
}

手写笔记辅助理解：

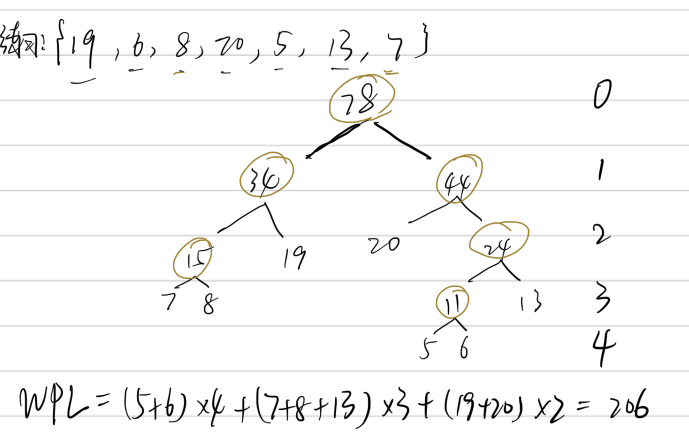
排序算法

选择排序

c 复制代码 
//交换函数
//
void swap(int* arr, int i,int j) {
	if (!arr || i < 0 || j < 0) return;
	if (i == j) return;
	int temp = arr[i];
	ar r[i] = arr[j];
	arr[j] = temp;
}
//选择排序（升序）
//双层循环 O（n^2),逐个比较
void selectionSort(int* arr, int n) {
	if (!arr || n <= 1) return;
	for (int i = 0;i < n;i++) {
		for (int j = 0;j < n;j++) {
			if (arr[i] > arr[j]) swap(arr, i, j);
		}
	}
}

冒泡排序

c 复制代码 
//冒泡排序（升序）
//每轮循环停止条件是i==j
//j就是本轮冒泡需要排序的位置
// 冒泡排序就是指每一轮循环中待排序的数会像冒泡泡一样移动到j-1的位置
void bubbleSort(int* arr, int n) {
	if (!arr || n <= 1) return;
	for (int j = n - 1;j >= 0;j--) {
		for (int i = 0;i < j;i++) {
			if (arr[i] > arr[i + 1]) swap(arr,i,i+1);
		}
	}
}
相关推荐
太理摆烂哥3 小时前
数据结构之并查集
数据结构
Knight_AL3 小时前
CMS vs G1 GC 写屏障：拦截时机与漏标的根本原因
java·jvm·算法
YGGP3 小时前
【Golang】LeetCode 75. 颜色分类
算法·leetcode
北山小恐龙3 小时前
针对性模型压缩：YOLOv8n安全帽检测模型剪枝方案
人工智能·深度学习·算法·计算机视觉·剪枝
涛涛北京3 小时前
【强化学习实验】- PPO
算法
2301_797312263 小时前
学习Java29天
java·算法
杜子不疼.4 小时前
【LeetCode 704 & 34_二分查找】二分查找 & 在排序数组中查找元素的第一个和最后一个位置
算法·leetcode·职场和发展
LYFlied4 小时前
【每日算法】LeetCode 437. 路径总和 III
前端·算法·leetcode·面试·职场和发展
宵时待雨5 小时前
C语言笔记归纳20：文件操作
c语言·开发语言·笔记·算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04BongoCat - 跨平台键盘猫动画工具05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07jdk21下载、安装（Windows、Linux、macOS）08sqli-labs靶场通关笔记：第18-19关 HTTP头部注入09Open-AutoGLM Windows 安装部署教程10RedissonClient的配置解析