前言
大家好,欢迎来到我们今天的主题:定点数的编码表示这一章节。
相信很多学C语言或C++的学弟学妹们都经历过这样一个"灵异事件":你定义了一个 int 类型的变量,给它赋值为大约 21 亿(具体是 231−12^{31}-1231−1),然后手贱给它加了个 1。结果呢?这个数瞬间变成了一个巨大的负数!
当时你的表情大概是这样的:🤯(WDF)。
为什么?计算机坏了?CPU 抽风了?
Nonono,这是计算机底层为你精心准备的一场"数字魔术"。要看懂这场魔术,我们就得钻进计算机肚子里,看看它是怎么用那一堆冷冰冰的"0"和"1"来表示我们现实世界中丰富多彩的数字的。
今天这篇博文,咱们不搞照本宣科那一套,我尽量用最通俗的话和最硬核的原理,带你彻底搞懂定点数、原码、反码、补码和移码这几个让无数初学者头大的概念。
定点数的"百变戏法"(原码、反码、补码、移码)
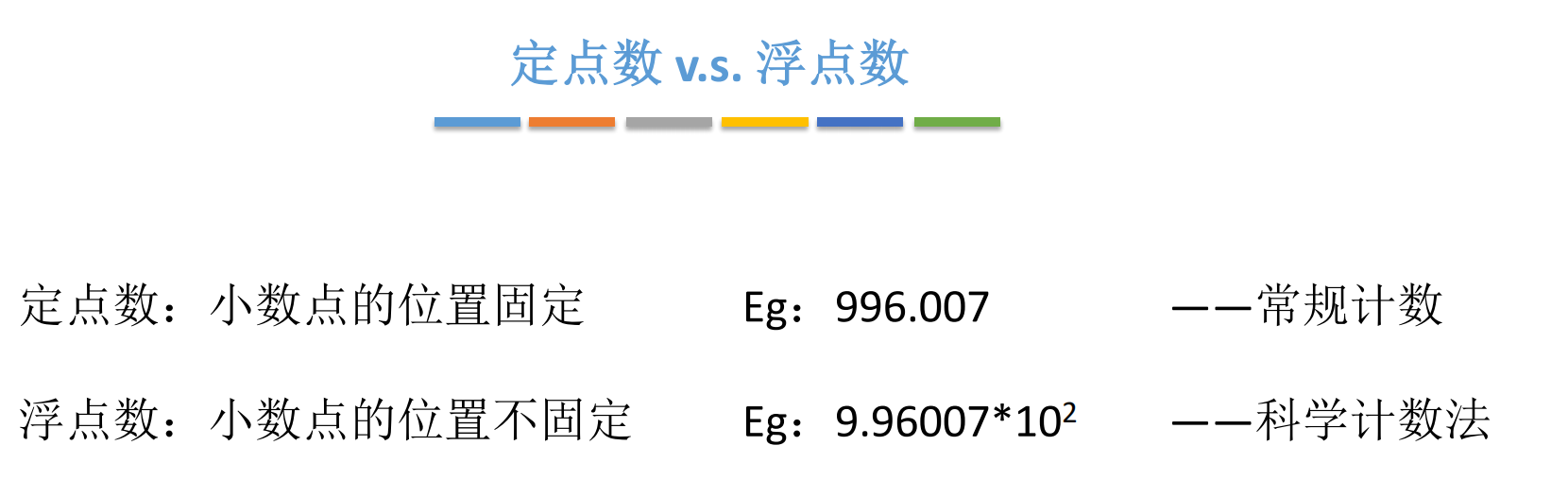
1. 开胃菜:定点数 VS 浮点数
在计算机的世界里,所有数据最终都是 0 和 1。要表示一个数,最大的问题是:小数点点在哪儿?
根据小数点位置是否固定,我们将数字的表示分为两大门派:
-
定点数 (Fixed-Point Number):
顾名思义,小数点的位置是死板的、固定不变的。这就好比我们平时去超市买菜,价格标签上写着 12.50 元,小数点永远在那两位小数前面。在计算机里,我们通常约定小数点要么在最后面(表示纯整数),要么在最前面(表示纯小数)。
-
浮点数 (Floating-Point Number):
小数点的位置是飘忽不定的。这就像科学计数法,比如 1.23×1051.23 \times 10^51.23×105 和 1.23×10−51.23 \times 10^{-5}1.23×10−5,虽然数字部分都是 123,但因为指数不同,小数点的位置实际上发生了"浮动"。浮点数是为了解决超大或超小数值表示而生的(这一部分我们后续章节细聊)。
本篇的主角,是定点数。 我们要看看,在小数点锁死的情况下,计算机怎么玩出花来。
2. "裸奔"的数字:无符号数 (Unsigned Number)
最简单粗暴的表示方式,就是无符号数。
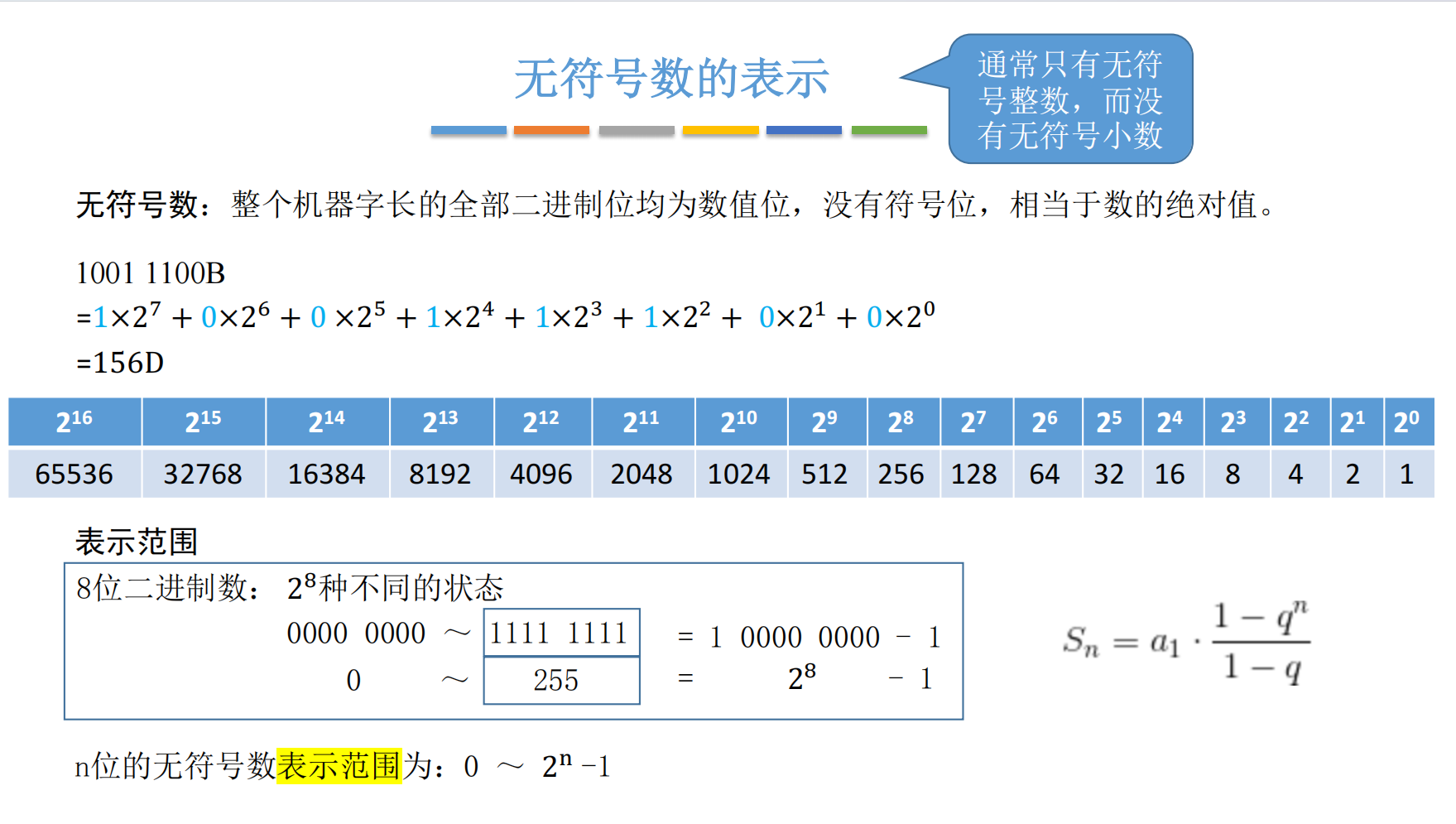
所谓"无符号",就是说整个机器字长(比如一个 8 bit 的寄存器)里所有的二进制位,全部用来表示数值本身,没有哪一位是拿来表示正负号的。默认大家都是正数(或者零)。
2.1 表示与计算
这跟我们小学学的二进制转十进制一模一样。每一位二进制数乘以它对应的"位权",然后相加。
假设我们有一个 8 位的无符号数,二进制是 10011100:
数值=1×27+0×26+0×25+1×24+1×23+1×22+0×21+0×20=128+0+0+16+8+4+0+0=156\begin{aligned} 数值 &= 1 \times 2^7 + 0 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \\ &= 128 + 0 + 0 + 16 + 8 + 4 + 0 + 0 \\ &= 156 \end{aligned}数值=1×27+0×26+0×25+1×24+1×23+1×22+0×21+0×20=128+0+0+16+8+4+0+0=156
2.2 表示范围
对于一个 nnn 位的无符号数:
-
最小值: 显然是所有位全为 0,即 00...000\dots000...0,真值为 000。
-
最大值: 显然是所有位全为 1,即 11...111\dots111...1。
这个全为 1 的值是多少呢?
-
笨办法: 2n−1+2n−2+⋯+202^{n-1} + 2^{n-2} + \dots + 2^02n−1+2n−2+⋯+20,这是一个等比数列求和,结果是 2n−12^n - 12n−1。
-
聪明办法: 假设这个数是 XXX (n个1)。如果我给 XXX 加 1,会发生什么?末位 1+11+11+1 变 000 进 111,一直连锁反应,最后变成了 111 后面跟 nnn 个 000,也就是 2n2^n2n。既然 X+1=2nX+1 = 2^nX+1=2n,那么 X=2n−1X = 2^n - 1X=2n−1。
结论:nnn 位无符号数的表示范围是 [0,2n−1][0, 2^n - 1][0,2n−1]。
例如,8位无符号数(C语言中的 unsigned char)的范围是 [0,28−1]=[0,255][0, 2^8-1] = [0, 255][0,28−1]=[0,255]。
无符号数通常只用来表示整数(在 C/C++ 中有 unsigned int, unsigned long 等,但没有 unsigned float)。
其最大的坑在于"下溢出"。
请大家看看这段代码,会不会死循环?
c
unsigned int i;
for (i = 10; i >= 0; --i) {
printf("%u\n", i);
}答案是:会!
因为当 i 等于 0 时,再减 1,它不会变成 -1,而是会变成无符号数的最大值(比如 32位下的 232−12^{32}-1232−1),这永远满足 i >= 0 的条件。这就是无符号数回绕(Wrapping)现象。
3. 有符号数的"四大金刚":原、反、补、移
现实世界是有负数的,计算机必须得能表示负数。对于定点数,我们通常把最高位腾出来,当作符号位 ,我们称为这个是有符号数。比如:1000 0010,这个最高位的1,代表着这个数是一个负数,数值由右边七位来决定,即:-2,0000 0010就是正2.
-
符号位 = 0 ,表示 正数。
-
符号位 = 1 ,表示 负数。
剩下的位(称为尾数)才用来表示数值的大小。
为了解决负数的存储和运算问题,聪明的计算机先驱们发明了四种编码方式,我称之为"四大金刚":原码、反码、补码、移码。
为了后续演示方便,我们统一假设机器字长为 8位。
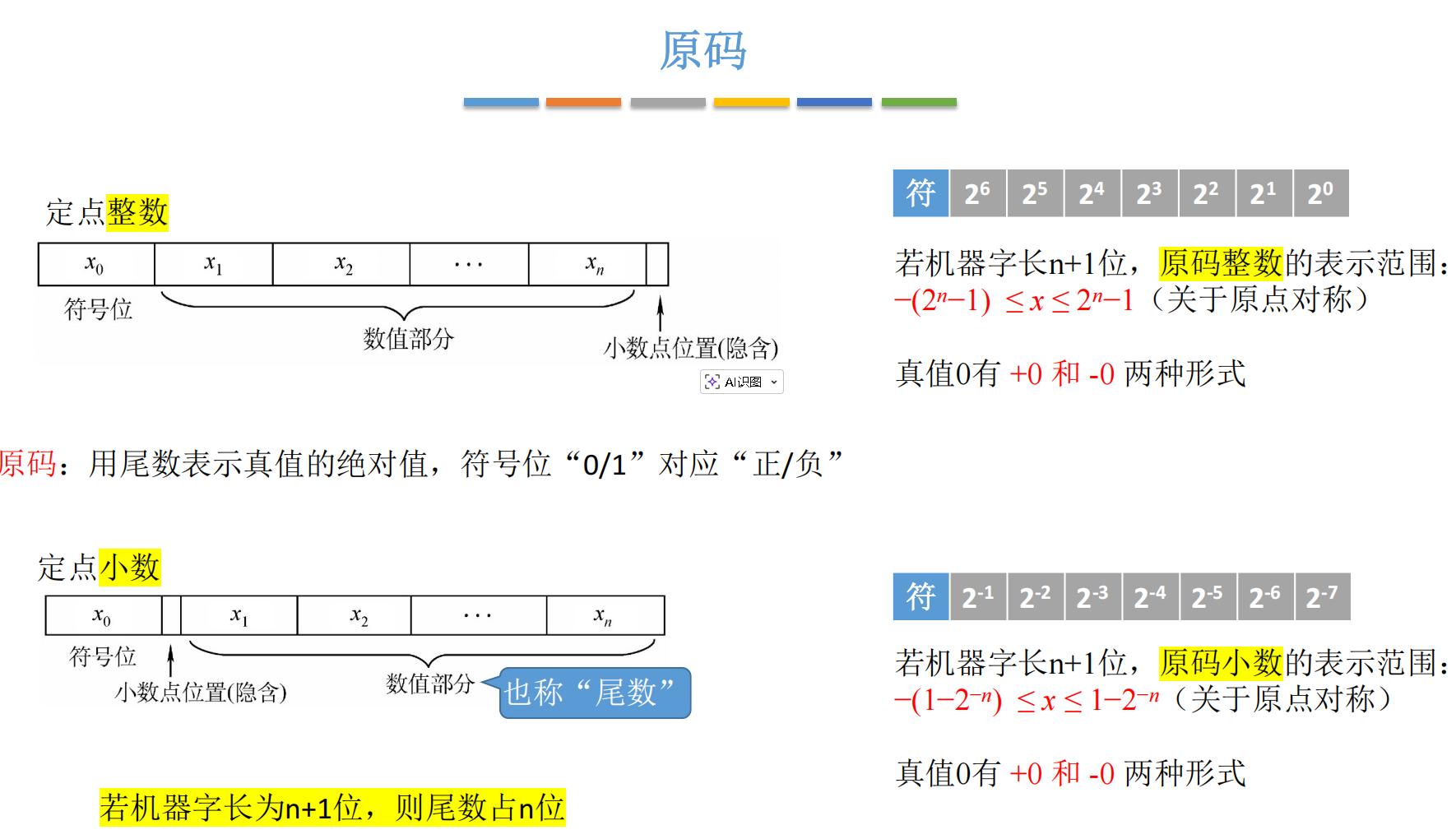
3.1 原码 (Sign-Magnitude):所见即所得
原码是最符合人类思维习惯的表示方法。
- 定义: 最高位为符号位,其余位表示数值的绝对值。
3.1.1 定点整数的原码
小数点隐含在最后一位的后面。
-
例:+19+19+19
-
符号位:正数 →0\rightarrow 0→0
-
数值位:19 的二进制是 100111001110011。我们要凑够 7 位尾数,前面补两个 0,变成 001001100100110010011。
-
[+19]原=00010011[+19]_{原} = 00010011[+19]原=00010011
-
-
例:−19-19−19
-
符号位:负数 →1\rightarrow 1→1
-
数值位:绝对值还是 19,尾数还是 001001100100110010011。
-
[−19]原=10010011[-19]_{原} = 10010011[−19]原=10010011
-
3.1.2 定点小数的原码
小数点隐含在符号位的后面,尾数的第一位权值是 2−1=0.52^{-1}=0.52−1=0.5,第二位是 2−2=0.252^{-2}=0.252−2=0.25,以此类推。
-
例:+0.75+0.75+0.75
-
0.75=0.5+0.25=2−1+2−20.75 = 0.5 + 0.25 = 2^{-1} + 2^{-2}0.75=0.5+0.25=2−1+2−2,二进制是 0.110.110.11。
-
符号位:000
-
数值位(凑够7位):110000011000001100000
-
[+0.75]原=0.1100000[+0.75]_{原} = 0.1100000[+0.75]原=0.1100000 (书上为了看得清楚,可能会写成 0.11000000.11000000.1100000 或者 0,11000000,11000000,1100000,那个点或逗号是给人看的,机器里不存在)
-
-
例:−0.75-0.75−0.75
-
符号位:111
-
数值位:110000011000001100000
-
[−0.75]原=1.1100000[-0.75]_{原} = 1.1100000[−0.75]原=1.1100000
-
3.1.3 原码的缺陷
原码看起来很美好,简单直观。但是它有两个致命的缺陷,导致现代计算机基本废弃了用它来进行整数运算:
-
"0"的表示不唯一:
-
+0\]原=00000000\[+0\]_{原} = 00000000\[+0\]原=00000000
-
一个数学上的 0,竟然占用了两个编码状态,我们称为正零与负零!这在硬件设计上是一个浪费,判断一个数是不是 0 还需要比较两次。
-
-
加减法运算极其复杂:
-
如果要做 1+(−1)1 + (-1)1+(−1),用原码表示就是 00000001+1000000100000001 + 1000000100000001+10000001。如果直接相加,结果是 100000101000001010000010,这是原码的 −2-2−2。结果显然错了!
-
为了用原码做加减法,CPU 的 ALU(算术逻辑单元)必须得先判断两个操作数的符号。如果是同号相加,就加绝对值;如果是异号相加(即减法),还得比较绝对值谁大,用大的减小的,最后还要确定结果的符号......
-
CPU 设计师:我太难了,这得增加多少逻辑电路啊!累吐血了!
-
为了解决这个问题,反码和补码应运而生。
3.2 反码 (One's Complement):尴尬的中间商
反码的出现是为了解决原码计算困难的问题,它是通往补码的必经之路。
-
定义:
-
正数: 反码和原码一模一样。(如假包换)
-
负数: 原码的符号位不变,尾数各位全部取反(0变1,1变0)。
-
-
例:+19+19+19
-
+19\]原=00010011\[+19\]_{原} = 00010011\[+19\]原=00010011
-
-
例:−19-19−19
-
−19\]原=10010011\[-19\]_{原} = \\mathbf{1}0010011\[−19\]原=10010011
-
[−19]反=11101100[-19]_{反} = 11101100[−19]反=11101100
-
-
例:−0.75-0.75−0.75
-
−0.75\]原=1.1100000\[-0.75\]_{原} = \\mathbf{1}.1100000\[−0.75\]原=1.1100000
-

反码的地位:
反码在现代计算机中几乎不作为最终的数据存储格式。它最大的问题是,它依然有两个0!
+0\]反=00000000\[+0\]_{反} = 00000000\[+0\]反=00000000
正零是全0,负零是全1。这依然很尴尬。反码现在更多的身份是"原码转补码的中间跳板"。
3.3 补码 (Two's Complement):计算机界的"真神"
这是本篇最重要的部分,也是面试最高频的考点。现代计算机系统中,整数一律采用补码来存储和运算!

3.3.1 补码的定义与转换
-
定义:
-
正数: 补码和原码、反码统统一样。(正数真是个好孩子)
-
负数: 在反码的基础上,末位加 1。
-
简而言之,负数补码的口诀:"符号位不变,尾数取反,末位加一"。
-
例:−19-19−19 求补码
-
写出原码:100100111001001110010011
-
求反码(尾数取反):111011001110110011101100
-
末位加一:11101100+1=1110110111101100 + 1 = 1110110111101100+1=11101101
-
[−19]补=11101101[-19]_{补} = 11101101[−19]补=11101101
-
-
例:−0.75-0.75−0.75 求补码
-
写出原码:1.11000001.11000001.1100000
-
求反码:1.00111111.00111111.0011111
-
末位加一:1.0011111+0.0000001=1.01000001.0011111 + 0.0000001 = 1.01000001.0011111+0.0000001=1.0100000 (注意进位!)
-
[−0.75]补=1.0100000[-0.75]_{补} = 1.0100000[−0.75]补=1.0100000
-
如何补码转回原码
已知一个负数的补码,怎么求原码?
很多同学会想着逆运算:"先减1,再取反"。这当然对。
但是,有一个更骚的操作:对补码再求一次补码,就回到了原码!
试一下:已知 [−19]补=11101101[-19]_{补} = 11101101[−19]补=11101101
符号位不变,尾数取反:100100101001001010010010
末位加一:10010010+1=1001001110010010 + 1 = 1001001110010010+1=10010011
这不就是 [−19]原[-19]_{原}[−19]原 吗?神不神奇!
记住:负数原码与补码的转换互为逆运算,操作逻辑完全一致。
3.3.2 深度硬核:为什么计算机要用补码?(核心考点)
补码不止解决了"0"的唯一性问题,这只是表象。补码真正的牛X之处在于它统一了加法和减法,拯救了 ALU 的设计师。
我们要引入一个概念:模运算 (Modulo Arithmetic)。
想象一个圆形的挂钟,上面有 0 到 11 一共 12 个刻度。这就构成了一个"模 12"的系统。

现在指针指向 2 点。如果不动指针,我想让它指向 1 点,有两种办法:
-
逆时针 拨 1 个格(相当于做减法:2−1=12 - 1 = 12−1=1)。
-
顺时针 拨 11 个格(相当于做加法:2+11=132 + 11 = 132+11=13)。在模 12 的世界里,13 实际上就是 1(13mod 12=113 \mod 12 = 113mod12=1)。
发现了吗?在模运算系统中,减去一个数,等于加上这个数对应的"补数"。 在模 12 系统中,-1 的补数就是 11(因为 ∣−1∣+11=12|-1| + 11 = 12∣−1∣+11=12)。
计算机的 nnn 位寄存器,本质上就是一个"模 2n2^n2n"的计数器。对于 8 位系统,模就是 28=2562^8 = 25628=256。
当我们用补码表示负数 −X-X−X 时,实际上存储的是 2n−∣X∣2^n - |X|2n−∣X∣。
现在来看看补码如何用加法器搞定减法运算 A−BA - BA−B:
我们把它看作 A+(−B)A + (-B)A+(−B)。我们在计算机里计算 [A]补+[−B]补[A]{补} + [-B]{补}[A]补+[−B]补。
A\]补+\[−B\]补=A+(2n−B)=2n+(A−B)\\begin{aligned} \[A\]_{补} + \[-B\]_{补} \&= A + (2\^n - B) \\\\ \&= 2\^n + (A - B) \\end{aligned}\[A\]补+\[−B\]补=A+(2n−B)=2n+(A−B) 由于我们的寄存器只有 nnn 位,这个结果中最前面的那个 2n2\^n2n(也就是最高位进位产生的一个 1,后面跟 n 个 0)会被直接**丢弃**(溢出舍弃)。 所以,最终寄存器里剩下的结果就是 A−BA - BA−B 的补码形式! **实战案例:用补码计算 2−22 - 22−2 (8位)** * 222 的补码:000000100000001000000010 * −2-2−2 的补码:原码 10000010→10000010 \\rightarrow10000010→ 反码 11111101→11111101 \\rightarrow11111101→ 补码 111111101111111011111110 直接相加: 00000010 (+2) + 11111110 (-2) ---------- 1 00000000 ↑ 最高位进位,丢弃! 结果是 `00000000`,正是 0 的补码!完美! **ALU 设计师喜极而泣:** 有了补码,我的 ALU 里面只需要设计一个加法器(Adder),就可以同时搞定加法和减法运算了!电路复杂度大大降低,运行效率咔咔提升。这就是补码被称为"神"的原因。 ##### 3.3.3 补码的细节:唯一的 0 和多出来的负数 **1. "0"的唯一性** * \[+0\]补=\[+0\]原=00000000\[+0\]_{补} = \[+0\]_{原} = 00000000\[+0\]补=\[+0\]原=00000000 * \[−0\]补\[-0\]_{补}\[−0\]补:原码 10000000→10000000 \\rightarrow10000000→ 反码 11111111→11111111 \\rightarrow11111111→ 末位加一,产生连续进位 →100000000\\rightarrow \\mathbf{1}00000000→100000000。最高位的 1 被丢弃,剩下 000000000000000000000000。 看到了吗?正负零的补码殊途同归,都是全 0。完美解决了原码和反码的问题。 2. 那个多出来的负数 细心的你可能会发现,在原码和反码中,100000001000000010000000 表示 −0-0−0。现在在补码中,−0-0−0 被合并没了,那 100000001000000010000000 这个二进制编码空出来了,它表示谁呢? 在补码系统中,我们人为规定,符号位为 1,尾数全为 0 的数,表示当前字长下能表示的**最小负数**。 * 对于 8 位整数,\[x\]补=10000000\[x\]_{补} = 10000000\[x\]补=10000000,它表示的真值是 −27=−128-2\^7 = -128−27=−128。 * 对于 8 位定点小数,\[x\]补=1.0000000\[x\]_{补} = 1.0000000\[x\]补=1.0000000,它表示的真值是 −1-1−1。 这个数很特殊,它是没有对应的原码和反码的(因为原码反码表示不了 -128)。 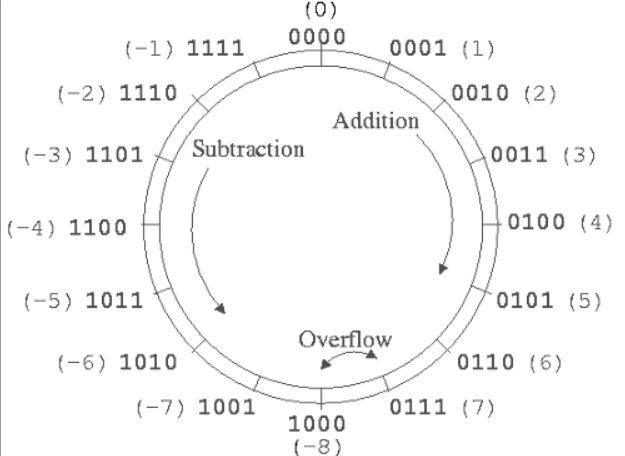 *** ** * ** *** #### 3.4 移码 (Excess Code / Offset Binary):为了比较而生 移码通常只用于表示整数。它的定义非常简单。 * **定义:** 在补码的基础上,**将符号位取反**。 * **例:+19+19+19** * \[+19\]补=00010011\[+19\]_{补} = \\mathbf{0}0010011\[+19\]补=00010011 * 符号位 0 变 1:**\[+19\]移=10010011\[+19\]_{移} = \\mathbf{1}0010011\[+19\]移=10010011** * **例:−19-19−19** * \[−19\]补=11101101\[-19\]_{补} = \\mathbf{1}1101101\[−19\]补=11101101 * 符号位 1 变 0:**\[−19\]移=01101101\[-19\]_{移} = \\mathbf{0}1101101\[−19\]移=01101101** 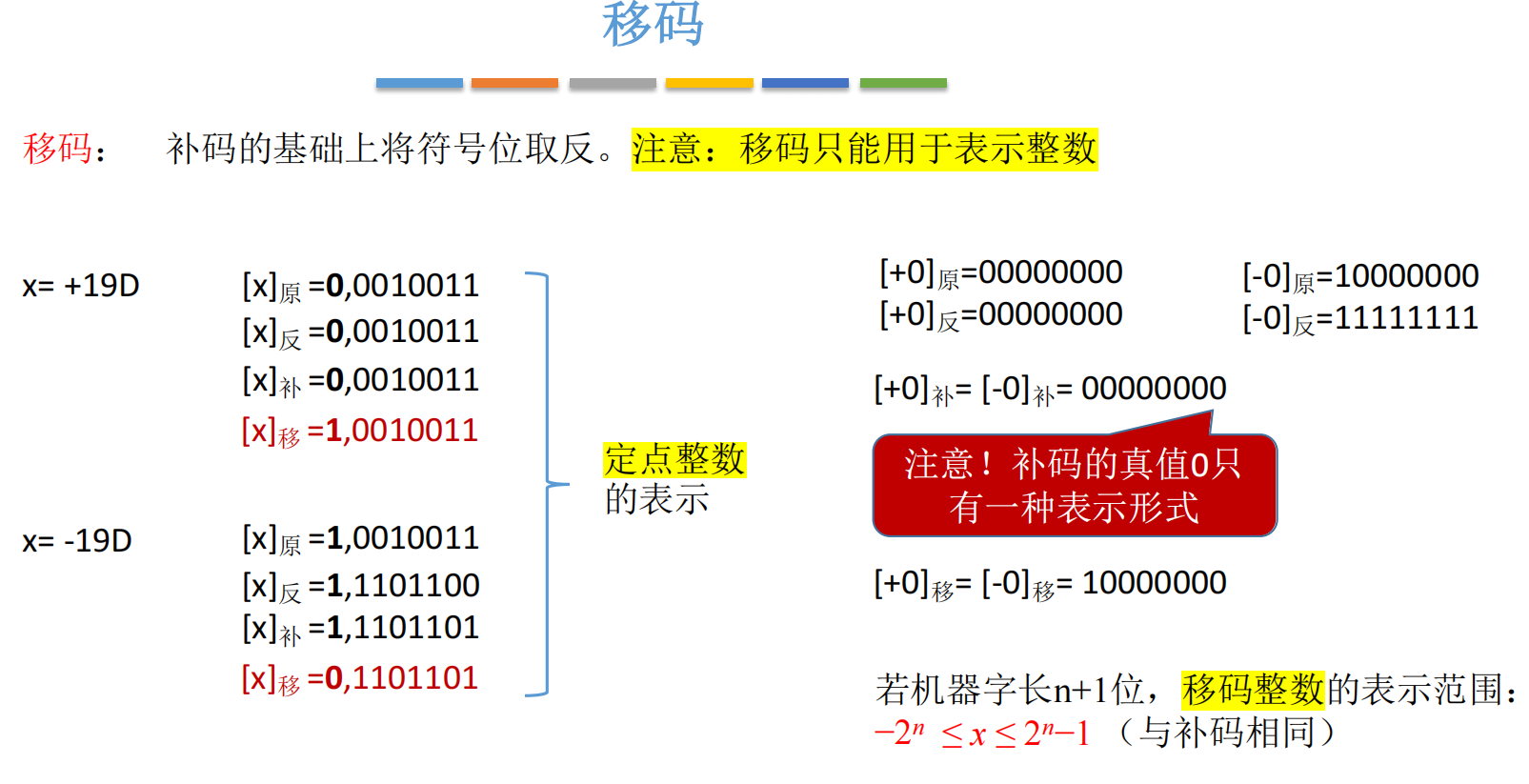 > **注意:** 也有教科书定义移码为"真值 + 偏置值(Bias)"。对于 n 位整数,偏置值通常取 2n2\^n2n 或 2n−12\^n-12n−1。我们这里采用王道书和大多数教材的定义:补码符号位取反(这等价于真值 + 2n2\^n2n)。 **为什么要有移码?** 看看上面的例子,正数的移码符号位是 1,负数的移码符号位是 0。这看起来很反直觉是不是? 移码最大的妙处在于,它把所有的负数映射到了正数区间,把正数映射到了更大的正数区间。这使得**我们可以像比较无符号数一样,直接比较两个移码的大小!** * 最小的数(例如 -128),其移码是 000000000000000000000000。 * 最大的数(例如 +127),其移码是 111111111111111111111111。 从全 0 到全 1,随着移码的值(当做无符号数看)增大,其对应的真值也是单调递增的。  **应用场景:** 移码主要用于\*\*浮点数的阶码(指数部分)\*\*表示。因为阶码即要有正也要有负,用移码表示后,硬件在比较两个浮点数的指数大小时,不需要考虑符号,直接按位比较即可,电路设计更简单。 *** ** * ** *** ### 4. 知识点大一统与表示范围盘点 这部分是考试的重灾区,一定要背下来,理解着背!我们假设机器字长为 n+1n+1n+1 位(1位符号位,n位尾数)。 | **编码方式** | **整数表示范围** | **小数表示范围** | **零的表示** | **备注** | |----------|-------------------------------------------------------------------|-----------------------------------------------------------------------------|---------------|-----------------------| | **原码** | \[−(2n−1),2n−1\]\[- (2\^n - 1), \\quad 2\^n - 1\]\[−(2n−1),2n−1\] | \[−(1−2−n),1−2−n\]\[- (1 - 2\^{-n}), \\quad 1 - 2\^{-n}\]\[−(1−2−n),1−2−n\] | 双重 (+0, -0) | 直观,计算复杂 | | **反码** | \[−(2n−1),2n−1\]\[- (2\^n - 1), \\quad 2\^n - 1\]\[−(2n−1),2n−1\] | \[−(1−2−n),1−2−n\]\[- (1 - 2\^{-n}), \\quad 1 - 2\^{-n}\]\[−(1−2−n),1−2−n\] | 双重 (+0, -0) | 中间状态 | | **补码** | **\[−2n,2n−1\]\[- 2\^n, \\quad 2\^n - 1\]\[−2n,2n−1\]** | **\[−1,1−2−n\]\[- 1, \\quad 1 - 2\^{-n}\]\[−1,1−2−n\]** | **唯一 (全0)** | **现代计算机标准,多表示一个最小负数** | | **移码** | \[−2n,2n−1\]\[- 2\^n, \\quad 2\^n - 1\]\[−2n,2n−1\] | (通常不用于小数) | 唯一 (符号位1,其余0) | 用于浮点数阶码,便于比较 | **重点记忆:** 1. **补码的整数范围比原码多一个最小负数**(比如 8 位是 -128 到 +127)。 2. **补码的小数范围可以取到 -1**,但取不到 +1。 3. 补码和移码的 0 都是唯一的。 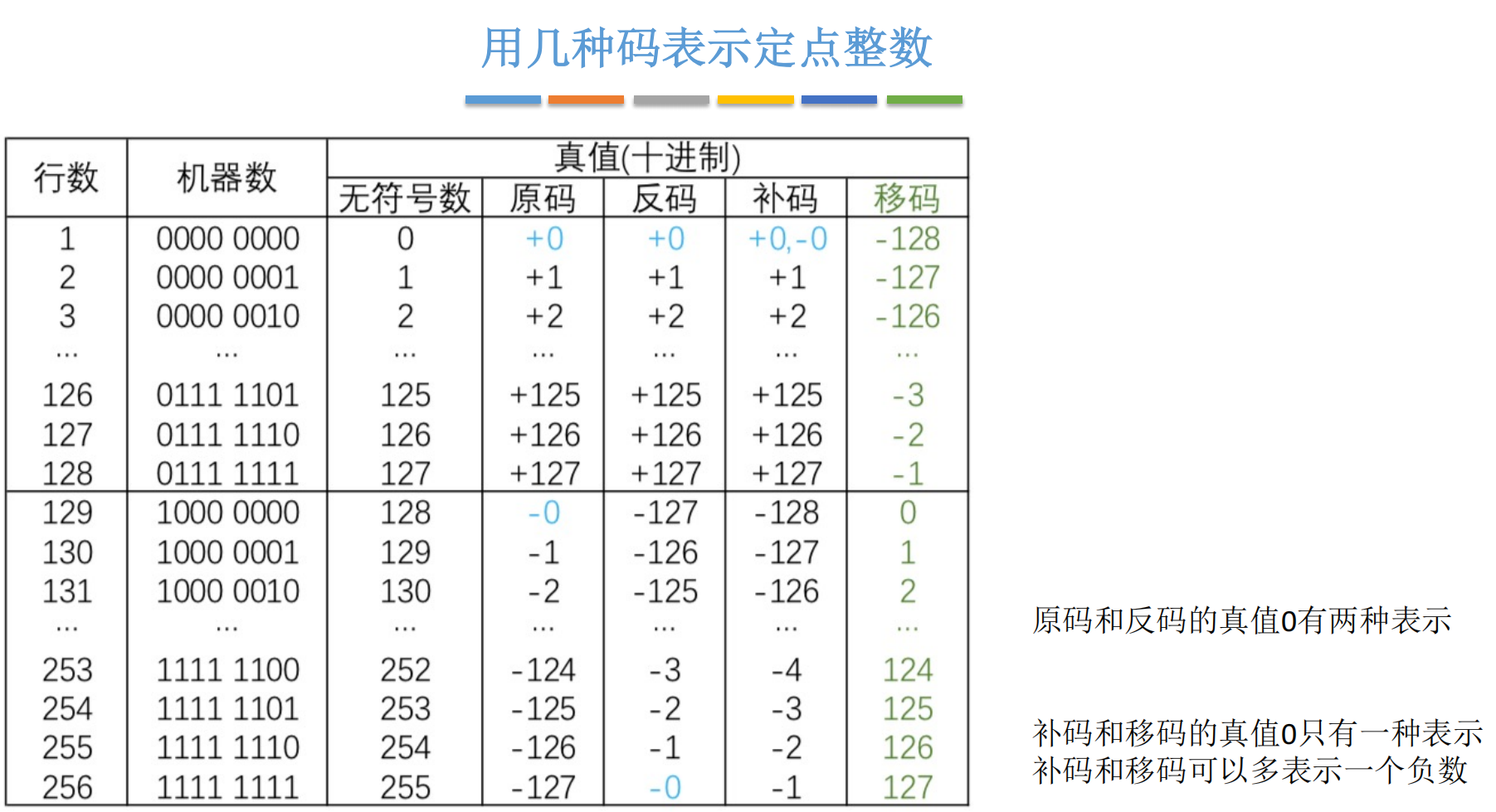 *** ** * ** *** ### 5. 实战演练与快速转换秘籍 光说不练假把式。我们拿两个数来练练手,假设是 8 位机器数。 #### 演练 1:真值 x=+50x = +50x=+50 1. **二进制:** 50=32+16+2=00110010250 = 32 + 16 + 2 = 00110010_250=32+16+2=001100102 2. **原码:** 正数符号位为 0 →00110010\\rightarrow \\mathbf{0}0110010→00110010 3. **反码:** 正数同原码 →00110010\\rightarrow \\mathbf{0}0110010→00110010 4. **补码:** 正数同原码 →00110010\\rightarrow \\mathbf{0}0110010→00110010 5. **移码:** 补码符号位取反 →10110010\\rightarrow \\mathbf{1}0110010→10110010 #### 演练 2:真值 x=−100x = -100x=−100 1. **二进制绝对值:** 100=64+32+4=011001002100 = 64 + 32 + 4 = 01100100_2100=64+32+4=011001002 2. **原码:** 负数符号位为 1 →11100100\\rightarrow \\mathbf{1}1100100→11100100 3. **反码:** 原码符号位不变,尾数取反 →10011011\\rightarrow \\mathbf{1}0011011→10011011 4. **补码:** 反码末位加 1 →10011011+1=10011100\\rightarrow 10011011 + 1 = \\mathbf{1}0011100→10011011+1=10011100 5. **移码:** 补码符号位取反 →00011100\\rightarrow \\mathbf{0}0011100→00011100 #### 手算补码的"骚操作" 考试或者面试时,为了求快,求负数补码(或从负数补码求原码)有一个无需经过反码的快速方法: **口诀:"从右往左找第一个 1,这个 1 和它右边的 0 保持不变,它左边的所有位(包括符号位)全部取反。"** 来试一下求 −100-100−100 的补码: * 原码:11100100111001\\mathbf{00}11100100 * 从右往左看,第一个 `1` 在第三位。 * 保留这个 `1` 和右边的 `00`,即 `...100`。 * 左边的 `1110` 全部取反变成 `0001`。 * 合体:10011100\\mathbf{1}001110010011100。 对比一下上面一步步算出来的结果,是不是一模一样?这个方法在做题时能帮你节省大量时间! *** ** * ** *** ### 总结  洋洋洒洒写了这么多,希望能帮你把这块硬骨头啃下来。 * 记住**定点数**就是小数点固定。 * 记住**无符号数**容易发生回绕。 * 记住**原码**最直观但计算最废柴。 * 记住**补码**是计算机计算的核心,它用模运算的魔法统一了加减法,还解决了 0 的唯一性问题。 * 记住**移码**是为了方便比较大小而生的。 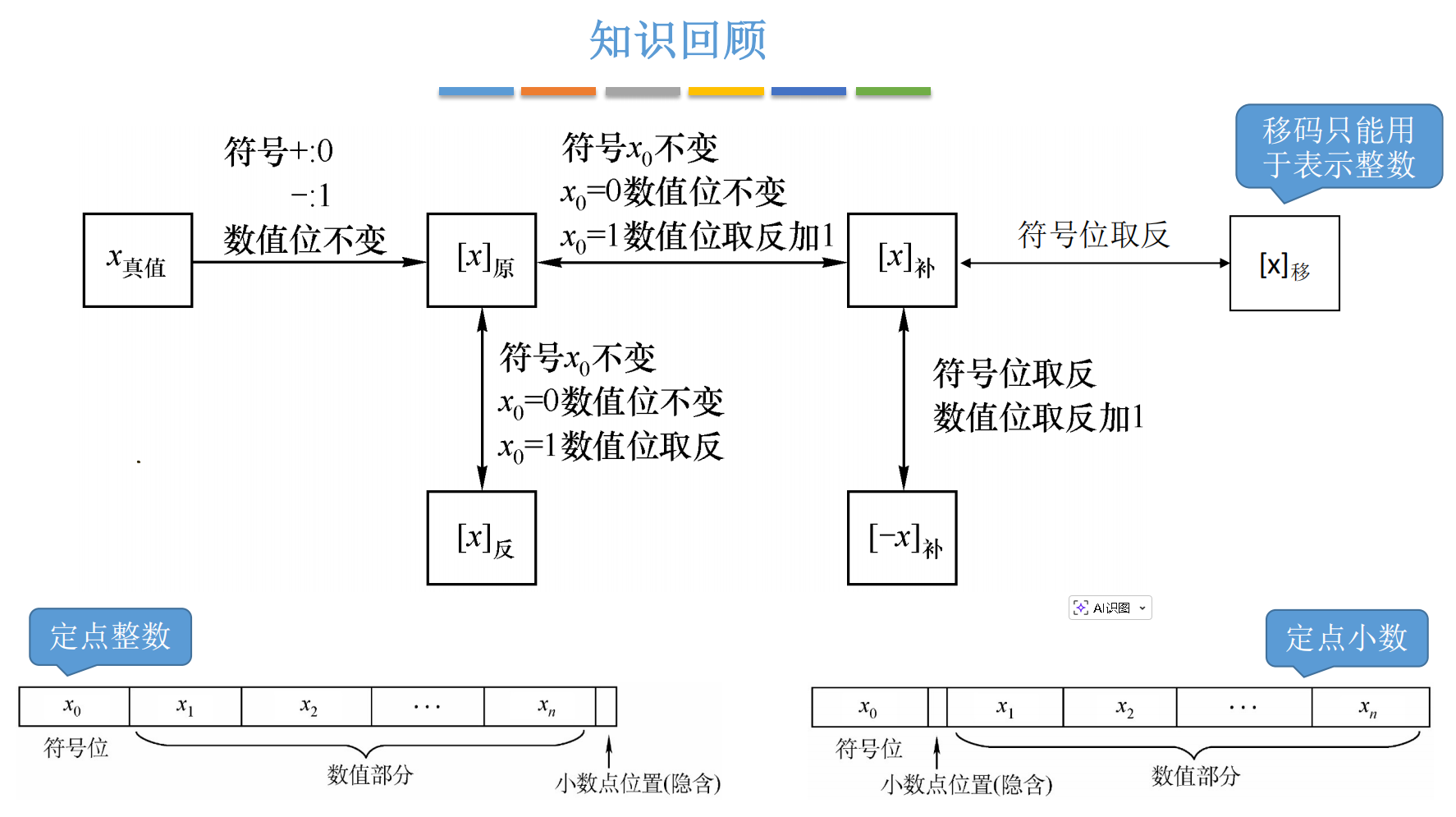 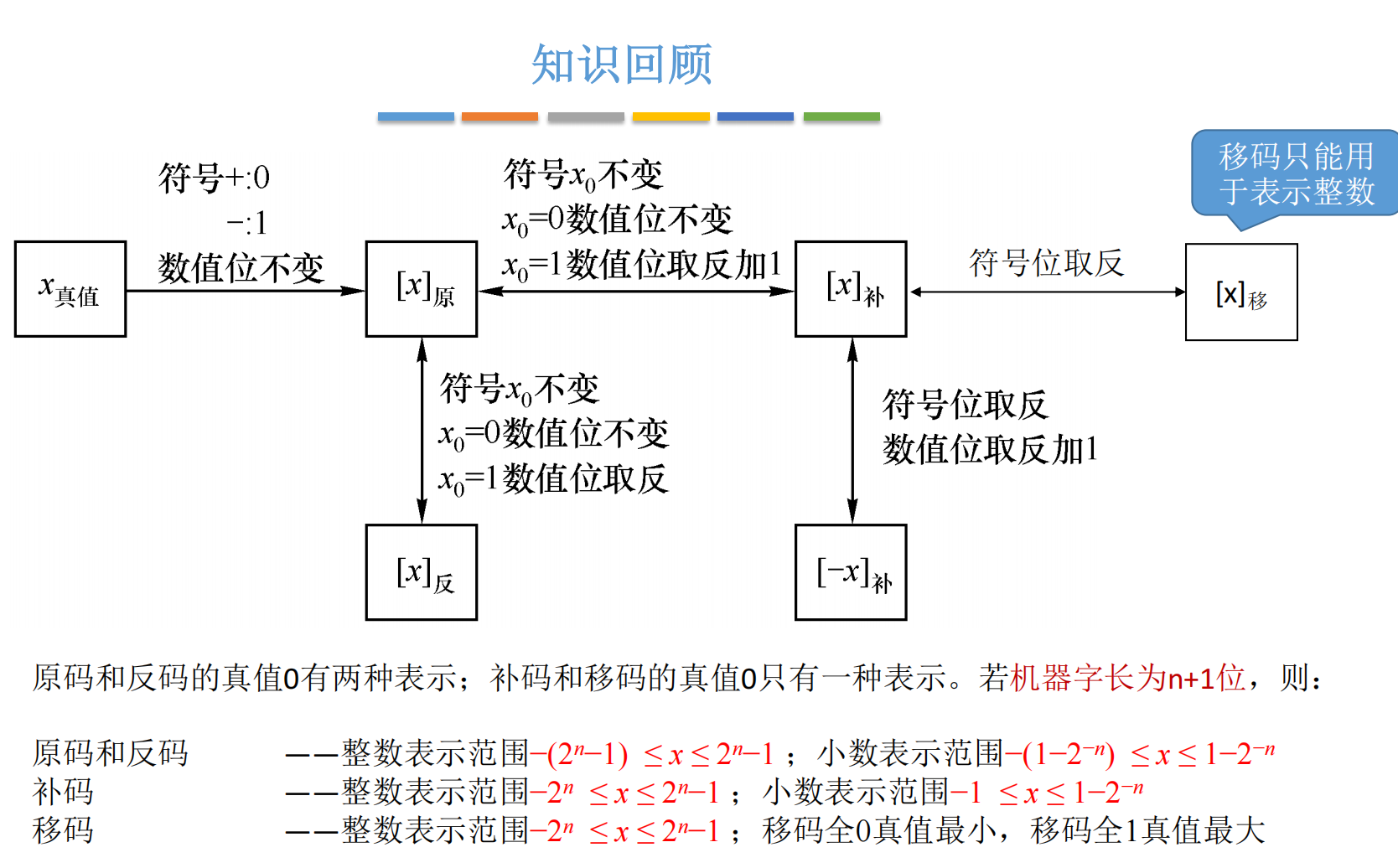 如果你觉得这篇博文对你有帮助,别忘了点赞、收藏、关注,我们下期见!
