概述
决策树是一种有监督学习算法，通过对训练样本学习建立分类或回归规则，以树状结构呈现，使所有数据从根节点逐步落到叶子节点得出预测结果。
决策树简单直观，无需数据预处理，能直接处理分类和回归任务，对缺失值不敏感，但容易过拟合，小样本下不稳定，单棵树精度通常不如集成方法。
节点
| 步骤 | 阶段 | 说明 |
|---|---|---|
| 1 | 根节点 | 所有数据进入根节点，依据首个最优特征进行第一次划分 |
| 2 | 非叶子节点 | 在中间节点按特征取值继续二分/多分，数据沿路径向下传递 |
| 3 | 叶子节点 | 数据抵达叶子节点，输出最终预测结果（类别或数值） |
| 本质逻辑 |
根节点：第一次划分的节点，包含全部训练样本。
中间节点（非叶子节点）：每次依据某特征的某个切分点，将数据分成子集后生成的节点；只要还能继续划分且满足继续分裂的条件，它就是中间节点。
叶子节点：无法继续分裂或达到停止条件的节点，直接输出预测结果。
节点分裂标准的依据
分裂的目标是让子节点比父节点更"纯"或更"精确"。常用指标如下：
分裂方式
离散特征
多叉分裂：按每个取值创建一个分支（ID3、C4.5）
二元分裂：将某些取值归为一类，其余归为另一类（CART）
连续特征
排序后尝试切分点（通常取相邻值的中点或分位数点），生成左右两个子集（CART、C4.5）
ID3算法
衡量标准熵值
熵（Entropy）源于信息论（Shannon 1948），用来度量一个系统的不确定性或信息量。
在决策树中，熵用来衡量数据集类别分布的混杂程度：
熵 = 0 → 数据完全纯净（所有样本属于同一类别）
熵越大 → 类别分布越均匀，越难预测
C4.5算法
C4.5 是分类决策树算法，核心目标与 ID3 一致------通过特征划分让子集更纯，但解决了 ID3 的几个关键短板：
在 ID3 算法中，我们用信息增益（IG）来选择划分特征：它会优先挑"取值多、能带来很多分支"的特征（比如"客户 ID"这种唯一标识类特征）。但这类特征往往对分类没有实际意义，只是把每个样本单独分成一类，属于"过拟合""无意义划分"。
为了克服这种"偏向于选择取值多的特征"的问题，C4.5 引入了 "信息增益比（Information Gain Ratio，IGR） 做归一化，让特征选择更合理。
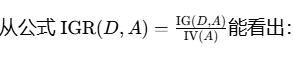
若特征 A取值特别多（比如"客户 ID"，每个客户对应唯一值），那么 IV(A)会很大（因为每个子集占比都很小，log后再求和处理后数值大）。此时就算 IG(D,A)不小，除以一个很大的 IV(A)后，IGR(D,A)也会被"拉低"。
→ 这就避免了像 ID3 那样，只因为某个特征取值多，就把无意义的特征选进来。
ID3选分裂特征时，容易偏爱取值多的无意义特征（比如"用户ID"），虽然按它划分后数据看起来很"纯"，但对实际分类毫无帮助。
C4.5的解决办法：用信息增益率（信息增益 ÷ 特征自身熵）选特征。
特征自身熵（固有值）：衡量特征取值的复杂程度（取值越多越分散，自身熵越高）。
核心逻辑：若特征取值极多（如ID），自身熵会很大 → 信息增益率被"惩罚"变低，避免被选中；反之，取值合理且能显著提升数据纯净度的特征，信息增益率更高，会被优先选为分裂依据。
结果：选出的特征既能让数据更纯净，又不会被无意义的多值特征干扰
CART算法
CART决策树通过最小化基尼指数选择分裂特征------基尼指数衡量数据的不纯度（值越小越纯净），对每个特征计算按其划分后所有子集的基尼指数总和，选择使总和最小的特征作为分裂点，从而让划分后的子集尽可能属于同一类别，实现高效且纯净的分类划分。
决策树剪枝
决策树剪枝是通过简化树结构来提升模型泛化能力的关键方法，核心目标是防止过拟合（即树过于复杂，记住训练数据噪声而非真实规律）。剪枝分为预剪枝和后剪枝两种主流策略，通常优先选择计算高效、效果稳定的预剪枝。
预剪枝
在树生成过程中提前停止分裂，常见策略包括：
限制树的深度（如最多5层）；
限制叶子节点数量或样本数（如每个叶子至少包含10个样本）；
设定基尼系数/信息增益阈值（如分裂后指标提升小于0.01则停止）。
优点：训练速度快，计算成本低；缺点：可能因过早停止错过潜在有用分支。
决策树优缺点
优点
简单直观：树形结构清晰呈现逻辑规则，易于理解。
无需标准化：数值特征无须缩放，直接输入模型。
兼容多类型：同时支持离散和连续特征混合输入。
耐受缺失值：对数据缺失不敏感，鲁棒性强。
多任务适用：可用于分类和回归两类问题。
缺点
容易过拟合：过度拟合训练数据中的噪声，泛化能力差。
小样本不稳定：数据量少时结果波动大。
类别不平衡敏感：少数类样本易被多数类主导。
精度局限：单棵树精度通常低于集成方法（如随机森林、XGBoost）。
决策树回归模型
决策树回归树）是通过递归划分特征空间，用叶节点样本均值预测连续型标签（如房价、消费额）的树形模型。
分类树用「纯度」（比如基尼系数、信息熵）来衡量划分好坏；
回归树用「误差最小化」来衡量划分好坏，最终每个叶子节点输出的是该区域内样本标签的均值。
整体建模流程可以概括为：
选择最优特征与最优切分点：遍历所有特征、所有可能的切分位置，找到能让"划分后左右子区域误差之和最小"的那个特征与切分点；
递归划分：把当前区域按照"最优特征+最优切分点"拆成左右两个子区域，对每个子区域重复步骤1，直到满足停止条件（比如节点样本数太少、误差下降不明显、达到预设最大深度等）；
叶子节点输出：每个叶子节点存储该区域内所有样本标签的均值，作为这个区域对未知样本的预测值。
回归树要解决的核心问题是：怎么切分，才能让划分后的区域"整体预测误差最小"？这里需要先定义"误差"的度量方式，最常见的就是 均方误差 和 平均绝对误差。
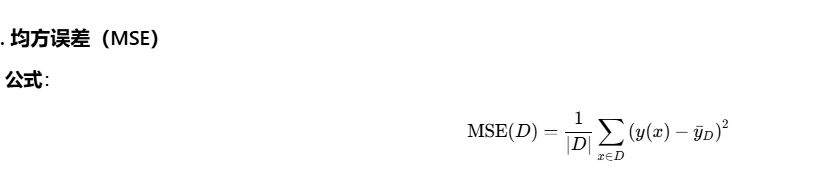衡量数据集 D中，所有样本真实值与均值的平方差的平均值，反映数据的离散程度
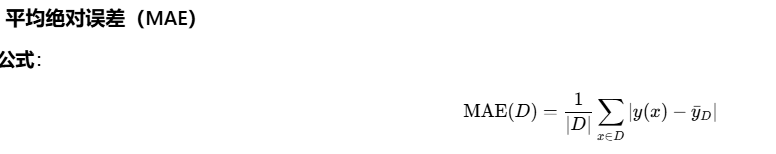
Scikit-learn中的决策树实现
核心参数
AUC
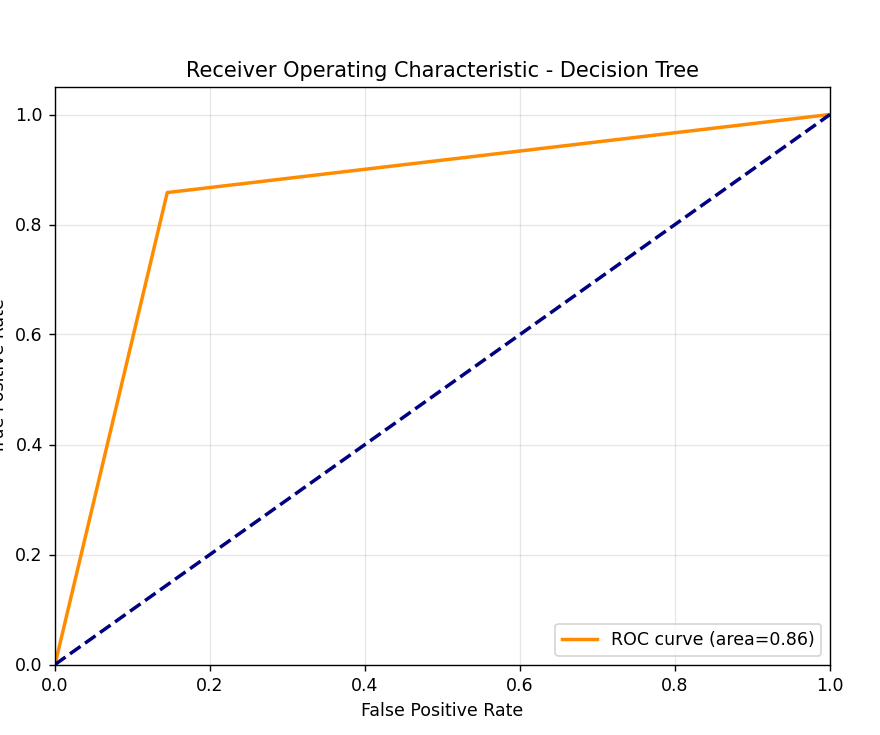
AUC 是ROC 曲线下方的面积，用于量化二分类模型区分正负样本的能力------AUC 越接近 1，模型排序能力越强；越接近 0.5，模型等同于随机猜测。
AUC-ROC曲线
AUC：曲线下面积，衡量模型对正负样本的区分能力
ROC：接收者操作特征曲线，显示不同阈值下真正例率和假正例率的关系
AUC 的优缺点
优点
全面反映分类能力：综合考虑了分类器对正例和负例的区分能力，体现模型在所有阈值下的整体表现。
样本不平衡下依然有效：不依赖正负样本比例，在类别分布悬殊时仍能客观评估模型性能。
稳健可靠：不受样本不平衡问题干扰，是相对稳健的评价指标，避免因多数类主导而产生误导。
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_curve, auc
# 生成示例数据
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建并训练决策树模型
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)
# 预测概率
y_pred_proba = clf.predict_proba(X_test)[:, 1] # 取正类的概率
# 计算ROC曲线和AUC
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
auc_result = auc(fpr, tpr)
# 绘制ROC曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area={auc_result:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic - Decision Tree')
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)
plt.show()
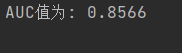
print(f"AUC值为: {auc_result:.4f}")
