目录
[为什么是低秩 ?](#为什么是低秩 ?)
[1、矩阵 B 初始化为零(B = 0)](#1、矩阵 B 初始化为零(B = 0))
[2、引入缩放因子 α / r(Scaling)](#2、引入缩放因子 α / r(Scaling))
[3、无额外推理开销:参数合并(Weight Merging)](#3、无额外推理开销:参数合并(Weight Merging))
为什么是低秩 ?
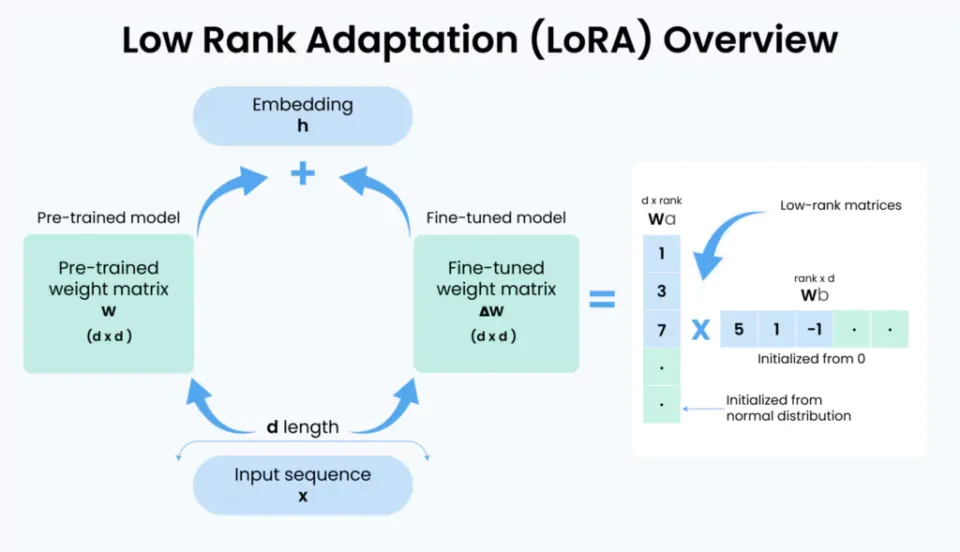
大量实证研究表明:大模型在微调过程中,权重增量矩阵 ΔW 具有显著的低内在秩(low intrinsic rank)。这意味着,尽管 ΔW 是一个高维矩阵(例如 4096×4096),其有效信息却集中在少数几个主成分上。
在 LoRA 中,矩阵 W 是模型的权重矩阵。而在传统的微调中,W 会直接进行调整,但在 LoRA 中,核心思想是将原始的权重矩阵 W 被分解为两个较小的低秩矩阵:A 和 B。这两个矩阵的乘积(A * B)就是对权重矩阵的调整部分:
ΔW = A × B
-
- A 是一个较小的矩阵,表示模型需要进行的最小调整。
- B 是另一个矩阵,将调整后的信息映射回原始权重空间。
通过这种低秩分解,LoRA 能够将微调过程中需要调整的参数数量大幅减少,同时保持原始模型的结构和基础知识不变。
低秩的选择?
在 LoRA 中,秩(r) 的选择非常关键。秩表示矩阵的"维度",它控制了低秩矩阵的参数数量。选择合适的秩是 LoRA 有效性的核心因素之一。
秩过大:如果选择的秩 r 太大,LoRA 的优势将被削弱,因为低秩矩阵的参数量仍然较大,无法有效减少计算和内存开销。
秩过小:如果秩选择过小,模型的拟合能力可能会下降,导致微调效果不佳。
在实际应用中,可以通过实验来选择最适合的秩值。通常,秩的大小会根据任务的复杂度和可用的计算资源进行调节。对于一般的应用场景,秩值通常设置在几到几十之间。
代码实现:
python
import torch
import torch.nn as nn
class LoRALinear(nn.Module):
def __init__(self, in_features: int, out_features: int, r: int, lora_alpha: int = 16):
super().__init__()
self.r = r
self.lora_alpha = lora_alpha
self.scaling = lora_alpha / r # 核心缩放因子
# 冻结原始权重(通常从预训练模型加载)
self.weight = nn.Parameter(
torch.empty(out_features, in_features),
requires_grad=False
)
# 低秩分解矩阵
self.lora_A = nn.Parameter(torch.zeros(r, in_features)) # shape: (r, d_in)
self.lora_B = nn.Parameter(torch.zeros(out_features, r)) # shape: (d_out, r)
# 初始化:A ~ N(0, σ²), B = 0 → 初始 ΔW = 0
nn.init.normal_(self.lora_A, std=1/r)
nn.init.zeros_(self.lora_B)
def forward(self, x: torch.Tensor) -> torch.Tensor:
# 主干路径:冻结权重计算
base_out = torch.nn.functional.linear(x, self.weight)
# LoRA 路径:低秩扰动
lora_out = (x @ self.lora_A.T) @ self.lora_B.T
# 合并输出
return base_out + lora_out * self.scaling在上述代码实现中,我们通过定义一个 LoRA 模块 ,为原始模型(如线性层)附加了两个低秩矩阵 A 与 B 。在前向传播阶段,模型会根据 A 和 B 的乘积对冻结的原始权重 W₀进行轻量级偏移,从而实现参数高效的微调。
从架构设计角度看,LoRA 在实现细节上有三个关键点:
1、矩阵 B 初始化为零(B = 0)
这是一项非常重要的架构决策。在训练初期,ΔW = B @ A = 0,意味着模型的行为与原始预训练模型 **保持完全一致,**这带来了两个优势:
-
(1)安全启动(Safe Warm-up):不会因为随机初始化造成模型预测突变,破坏预训练知识体系。
-
(2)快速收敛(Stable Convergence):从稳定基线开始学习,优化路径更平滑。
2、引入缩放因子 α / r(Scaling)
LoRA 在结构中使用了一个可学习的缩放因子:
ΔW=(B@A)×rα
其中:
-
r:低秩矩阵的秩(rank),决定可训练自由度
-
α:缩放系数,用于控制更新强度
这种设计的架构价值在于:
-
(1)统一学习率(LR Invariance):即使 r 发生变化,微调强度仍然稳定,不需要重新寻找学习率等超参数。
-
(2)提高鲁棒性与部署便捷度:不同任务、不同结构间迁移更容易。
3、无额外推理开销:参数合并(Weight Merging)
LoRA 的另一个工程亮点是推理阶段 零额外计算。训练完成后,可以把低秩更新合并回原始权重:
Wmerged=W0+(B@A)×rα
合并后:
-
模型不再需要 A、B,也不再计算矩阵乘法
-
推理路径 完全与原模型一致
-
延迟(latency)与吞吐(throughput)保持不变
这让 LoRA 在实际部署中极具性价比,非常适合用于边缘设备、本地模型运行以及大规模在线推理服务。------ 在效果追平全量微调的前提下,将训练成本降低一个数量级,同时解决多任务部署的存储 / 推理痛点。
综上所述,LoRA 本质上是对大模型微调方式的一次"降维重构":它利用了"大模型知识高度结构化"的事实,将任务适配压缩到更低维度的流形(Manifold)上,以最小扰动实现最大适应。
适配场景:
| 场景 | 有效性原因 | 效果表现 |
|---|---|---|
| 小样本下游任务 | 少量参数微调不易过拟合,保留预训练知识 | 效果超全量微调 |
| 大模型轻量化微调 | 单卡即可训练,无需分布式集群 | 训练成本降低 90%+ |
| 多任务快速适配 | 每个任务仅保存 LoRA 权重(MB 级) | 存储成本降低千倍 |
| 工业级推理部署 | 合并 LoRA 权重后无推理延迟 | 推理速度与原模型一致 |
参考: