《Java数据结构与算法》第四篇（四）：二叉树的高级操作查找与删除实现详解

一起养小猫2025-12-22 12:41

《Java数据结构与算法》第四篇（四）：二叉树的高级操作------查找与删除的实现详解

摘要： 本文深入探讨二叉树的两种核心操作：查找（Search）和删除（Delete）。通过详细的算法分析、完整的Java代码实现、丰富的图表示例，帮助读者掌握二叉树动态操作的关键技术。文章涵盖了递归与非递归查找算法、四种删除情况的详细处理、时间复杂度分析，以及与前端DOM操作的对比思考。

📖 目录

一、二叉树查找操作概述

1.1 查找操作的重要性

在数据结构的学习中，**查找（Search）**是最基本也是最重要的操作之一。二叉树的查找操作不仅是理解树形结构的关键，更是后续学习更复杂数据结构（如二叉搜索树、平衡树、B树等）的基础。

查找操作的核心目标： 在给定的二叉树中找到具有特定值的节点，或者确定该节点不存在。

1.2 二叉树查找的特点

与线性数据结构的查找不同，二叉树的查找具有以下特点：

  • 非线性查找： 需要在多个分支中进行选择
  • 路径多样性： 从根到目标节点可能有多条路径
  • 递归性： 树的递归性质使得递归查找算法自然简洁
  • 访问控制： 查找过程中可以灵活控制节点的访问顺序

1.3 查找算法分类

根据实现方式的不同，二叉树查找可以分为：

  1. 递归查找： 代码简洁，符合树的递归本质
  2. 非递归查找： 使用栈结构，空间效率更高
  3. 深度优先查找（DFS）： 沿着一条路径深入搜索
  4. 广度优先查找（BFS）： 按层次逐层搜索

二、递归查找算法实现

2.1 递归查找的算法思想

递归查找充分利用了二叉树的递归性质，将复杂问题分解为简单的子问题。基本思想如下：

  1. 基本情况： 如果当前节点为空，说明查找失败，返回null
  2. 匹配情况： 如果当前节点值等于目标值，查找成功，返回当前节点
  3. 递归情况： 先在左子树中查找，如果未找到再在右子树中查找

2.2 递归查找的Java实现

java 复制代码 
// 二叉树查找功能 - 递归版本
public BiTreeNode searchRecursive(char target) {
    return searchRecursiveHelper(root, target);
}

private BiTreeNode searchRecursiveHelper(BiTreeNode node, char target) {
    // 基本情况：空节点
    if (node == null) {
        return null;
    }

    // 基本情况：找到目标节点
    if (node.data == target) {
        return node;
    }

    // 递归情况：先在左子树中查找
    BiTreeNode leftResult = searchRecursiveHelper(node.lchild, target);
    if (leftResult != null) {
        return leftResult;
    }

    // 递归情况：如果左子树没找到，则在右子树中查找
    return searchRecursiveHelper(node.rchild, target);
}

2.3 递归查找的执行流程分析

让我们以查找节点'E'为例，分析递归查找的执行过程：

复制代码 
查找目标：E
二叉树结构：
     A
    / \
   B   C
  / \
 D   E

执行轨迹：
A(0) ──→ 不匹配，查找左子树
  ├─ B(1) ──→ 不匹配，查找左子树
  │   ├─ D(2) ──→ 不匹配，左子树为null
  │   │   └─ null(3) ──→ 返回null
  │   └─ 右子树查找 E(4) ──→ 匹配！返回节点E
  └─ 无需查找右子树

2.4 递归查找的优缺点

优点：

  • 代码简洁优雅，易于理解
  • 符合数学定义，自然表达了树的递归性质
  • 便于调试和维护

缺点：

  • 存在栈溢出风险（树很深时）
  • 递归调用有一定的性能开销
  • 空间复杂度为O(h)，h为树的高度

深度思考： 递归算法的优雅性来源于其分治思想------将大问题分解为结构相同的小问题。这种思想不仅适用于树结构，也是整个算法设计中的重要范式。

三、非递归查找算法实现

3.1 非递归查找的算法思想

非递归查找通过使用**栈（Stack）**数据结构来模拟递归调用过程。核心思想是：

  1. 使用栈保存待访问的节点
  2. 采用深度优先搜索策略
  3. 通过循环代替递归调用

3.2 非递归查找的Java实现

java 复制代码 
// 二叉树查找功能 - 非递归版本（使用栈）
public BiTreeNode searchIterative(char target) {
    if (root == null) {
        return null;
    }

    Stack<BiTreeNode> stack = new Stack<>();
    stack.push(root);  // 根节点入栈

    while (!stack.isEmpty()) {
        BiTreeNode curr = stack.pop();  // 弹出栈顶节点

        // 检查当前节点是否匹配
        if (curr.data == target) {
            return curr;  // 找到目标节点
        }

        // 右子节点先入栈（后处理）
        if (curr.rchild != null) {
            stack.push(curr.rchild);
        }

        // 左子节点后入栈（先处理）
        if (curr.lchild != null) {
            stack.push(curr.lchild);
        }
    }

    return null;  // 未找到目标节点
}

3.3 非递归查找的关键细节

栈的入栈顺序是一个重要细节：

  1. 右子节点先入栈：保证左子节点先被处理
  2. 左子节点后入栈：利用栈的LIFO特性
  3. 顺序不可颠倒：否则会改变遍历顺序

这种设计确保了算法按照前序遍历的顺序进行查找。

3.4 非递归查找的执行轨迹

java 复制代码 
// 执行轨迹示例（查找节点'E'）
Stack变化过程：
初始化：[A]

第1次循环：
- pop() → A
- A ≠ 'E'
- push(C), push(B)
- Stack: [C, B]

第2次循环：
- pop() → B
- B ≠ 'E'
- push(E), push(D)
- Stack: [C, E, D]

第3次循环：
- pop() → D
- D ≠ 'E'
- 无子节点入栈
- Stack: [C, E]

第4次循环：
- pop() → E
- E == 'E'
- 返回节点E

3.5 递归与非递归查找的对比

对比维度 递归查找 非递归查找
代码简洁性 优秀（约10行） 一般（约20行）
空间效率 O(h)递归栈 O(h)显式栈
时间效率 稍慢（调用开销） 稍快（无调用开销）
栈溢出风险 存在 不存在
可读性 高 中等
调试难度 较难 较易

四、二叉树删除操作概述

4.1 删除操作的复杂性

相比于查找操作，**删除（Delete）**操作要复杂得多。删除操作不仅要找到目标节点，还要处理删除后树结构的重构，确保：

  1. 结构完整性： 删除后仍是一棵有效的二叉树
  2. 连接正确性： 父子关系必须正确维护
  3. 无内存泄漏： 被删除节点的内存要正确释放
  4. 节点计数： 树的节点数量要正确更新

4.2 删除操作的核心挑战

删除操作的主要挑战在于处理不同的节点情况：

  • 叶子节点： 直接删除，无副作用
  • 单子节点： 用子节点替换被删除节点
  • 双子节点： 最复杂的情况，需要找到合适的替代节点

4.3 删除操作的设计原则

  1. 分类处理： 根据节点的子节点数量采用不同策略
  2. 保持连接： 确保删除后的父子节点关系正确
  3. 最小影响： 尽量减少对树结构的改动
  4. 状态同步： 及时更新树的节点计数等信息

五、删除操作的四种情况分析

5.1 情况一：删除叶子节点

叶子节点是指没有子节点的节点。这是最简单的删除情况。

处理策略： 直接删除，将其父节点对应的子节点指针设为null。

java 复制代码 
// 情况1：目标节点是叶子节点
if (targetNode.lchild == null && targetNode.rchild == null) {
    if (isLeftChild) {
        parent.lchild = null;
    } else {
        parent.rchild = null;
    }
}

图解说明：

复制代码 
删除前：
     A
    / \
   B   C
  /
 D

删除节点D后：
     A
    / \
   B   C

5.2 情况二：删除只有左子节点的节点

处理策略： 用被删除节点的左子节点替换被删除节点。

java 复制代码 
// 情况2：目标节点只有左子节点
else if (targetNode.rchild == null) {
    if (isLeftChild) {
        parent.lchild = targetNode.lchild;
    } else {
        parent.rchild = targetNode.lchild;
    }
}

图解说明：

复制代码 
删除前：
     A
    / \
   B   C
  /
 D
/
E

删除节点B后：
     A
    / \
   D   C
  /
 E

5.3 情况三：删除只有右子节点的节点

处理策略： 用被删除节点的右子节点替换被删除节点。

java 复制代码 
// 情况3：目标节点只有右子节点
else if (targetNode.lchild == null) {
    if (isLeftChild) {
        parent.lchild = targetNode.rchild;
    } else {
        parent.rchild = targetNode.rchild;
    }
}

图解说明：

复制代码 
删除前：
     A
    / \
   B   C
    \
     D

删除节点B后：
     A
    / \
   D   C

5.4 情况四：删除有两个子节点的节点

这是最复杂的情况，需要特别处理。这里我发现了一个有趣的现象，这种删除策略和前端DOM元素删除有很多相似之处。

核心策略： 找到右子树的最小节点（最左边的节点），用其值替换被删除节点的值，然后删除该最小节点。（这里也可以是左子树的最右节点）

前端对比思考： 在前端开发中，当我们需要删除一个有子元素的DOM节点时，我们通常需要决定如何处理其子元素。是全部删除，还是将子元素移动到其他位置？这与二叉树删除双子节点的情况非常相似。我们选择右子树的最小节点作为替代，就像是把某个子元素重新"挂载"到被删除节点的位置。

java 复制代码 
// 情况4：目标节点有两个子节点
else {
    // 找到右子树的最小节点（左下角的节点）
    BiTreeNode minNode = targetNode.rchild;
    BiTreeNode minParent = targetNode;

    while (minNode.lchild != null) {
        minParent = minNode;
        minNode = minNode.lchild;
    }

    // 用最小节点的值替换目标节点的值
    targetNode.data = minNode.data;

    // 删除最小节点（最小节点必然没有左子节点）
    if (minParent == targetNode) {
        minParent.rchild = minNode.rchild;
    } else {
        minParent.lchild = minNode.rchild;
    }
}

为什么选择右子树的最小节点？

  1. 保持二叉搜索树性质： 如果是二叉搜索树，这样能保持排序性质
  2. 简化删除操作： 最小节点必然没有左子节点，删除简化为情况1或3
  3. 结构稳定： 对树结构的影响最小

图解说明：

复制代码 
删除前：
     A
    / \
   B   C
  / \
 D   E
    /
   F

删除节点B的过程：
1. 找到B的右子树的最小节点：F
2. 用F替换B：
     A
    / \
   F   C
  / \
 D   E

3. 删除原F节点（最终结果）：
     A
    / \
   F   C
  / \
 D   E

5.5 根节点删除的特殊处理

根节点的删除需要特殊处理，因为它没有父节点：

java 复制代码 
// 删除根节点的辅助方法
private BiTreeNode deleteRootNode(BiTreeNode rootNode) {
    if (rootNode.lchild == null && rootNode.rchild == null) {
        return null;  // 根节点是叶子节点
    }
    if (rootNode.lchild == null) {
        return rootNode.rchild;  // 只有右子节点
    }
    if (rootNode.rchild == null) {
        return rootNode.lchild;  // 只有左子节点
    }

    // 根节点有两个子节点的情况
    BiTreeNode minNode = rootNode.rchild;
    BiTreeNode minParent = rootNode;

    while (minNode.lchild != null) {
        minParent = minNode;
        minNode = minNode.lchild;
    }

    rootNode.data = minNode.data;

    if (minParent == rootNode) {
        minParent.rchild = minNode.rchild;
    } else {
        minParent.lchild = minNode.rchild;
    }

    return rootNode;
}

六、完整代码实现与测试案例

6.1 完整的删除操作实现

java 复制代码 
/**
 * 删除节点功能 - 返回是否删除成功
 *
 * 删除操作的四种情况：
 * 1. 删除叶子节点：直接将其父节点的对应子节点指针置为null
 * 2. 删除只有左子节点的节点：用其左子节点替换该节点
 * 3. 删除只有右子节点的节点：用其右子节点替换该节点
 * 4. 删除有两个子节点的节点：找到右子树的最小节点，用其值替换目标节点，然后删除最小节点
 */
public boolean deleteNode(char target) {
    if (root == null) {
        return false;
    }

    // 特殊情况：要删除的是根节点
    if (root.data == target) {
        root = deleteRootNode(root);
        num = countNodes(root); // 重新计算节点数
        return true;
    }

    // 查找要删除的节点及其父节点
    BiTreeNode parent = null;
    BiTreeNode targetNode = null;

    // 层次遍历查找目标节点和其父节点
    Stack<BiTreeNode> stack = new Stack<>();
    Stack<BiTreeNode> parentStack = new Stack<>();
    stack.push(root);
    parentStack.push(null);

    while (!stack.isEmpty()) {
        BiTreeNode curr = stack.pop();
        BiTreeNode currParent = parentStack.pop();

        if (curr.data == target) {
            parent = currParent;
            targetNode = curr;
            break;
        }

        if (curr.lchild != null) {
            stack.push(curr.lchild);
            parentStack.push(curr);
        }
        if (curr.rchild != null) {
            stack.push(curr.rchild);
            parentStack.push(curr);
        }
    }

    if (targetNode == null) {
        return false; // 未找到目标节点
    }

    // 执行删除操作
    // 判断目标节点是父节点的左子节点还是右子节点
    boolean isLeftChild = (parent != null && parent.lchild == targetNode);

    // 情况1：目标节点是叶子节点
    if (targetNode.lchild == null && targetNode.rchild == null) {
        if (isLeftChild) {
            parent.lchild = null;
        } else {
            parent.rchild = null;
        }
    }
    // 情况2：目标节点只有左子节点
    else if (targetNode.rchild == null) {
        if (isLeftChild) {
            parent.lchild = targetNode.lchild;
        } else {
            parent.rchild = targetNode.lchild;
        }
    }
    // 情况3：目标节点只有右子节点
    else if (targetNode.lchild == null) {
        if (isLeftChild) {
            parent.lchild = targetNode.rchild;
        } else {
            parent.rchild = targetNode.rchild;
        }
    }
    // 情况4：目标节点有两个子节点
    else {
        // 找到右子树的最小节点（左下角的节点）
        // 这种方法保证了二叉搜索树的性质被保持
        BiTreeNode minNode = targetNode.rchild;
        BiTreeNode minParent = targetNode;

        while (minNode.lchild != null) {
            minParent = minNode;
            minNode = minNode.lchild;
        }

        // 用最小节点的值替换目标节点的值
        targetNode.data = minNode.data;

        // 删除最小节点（最小节点必然没有左子节点）
        if (minParent == targetNode) {
            minParent.rchild = minNode.rchild;
        } else {
            minParent.lchild = minNode.rchild;
        }
    }

    num = countNodes(root); // 重新计算节点数
    return true;
}

6.2 综合测试案例

java 复制代码 
public static void main(String[] args) {
    BiTree biTree = new BiTree();

    // 测试用例: 二叉树 A B D # # E # # C # #
    String input = "ABD##E##C##";
    biTree.createBiTree(input);

    System.out.println("=== 二叉树查找和删除功能测试 ===");

    // 查找功能测试
    System.out.println("4. 查找功能测试:");

    // 测试递归查找
    char target1 = 'D';
    BiTreeNode foundNode1 = biTree.searchRecursive(target1);
    if (foundNode1 != null) {
        System.out.println("递归查找: 找到节点 " + target1);
    } else {
        System.out.println("递归查找: 未找到节点 " + target1);
    }

    // 测试非递归查找
    char target2 = 'E';
    BiTreeNode foundNode2 = biTree.searchIterative(target2);
    if (foundNode2 != null) {
        System.out.println("非递归查找: 找到节点 " + target2);
    } else {
        System.out.println("非递归查找: 未找到节点 " + target2);
    }

    // 删除功能测试
    System.out.println("\n5. 删除节点功能测试:");
    System.out.println("删除前的树结构 (前序遍历): " + biTree.DLR3());

    // 删除叶子节点测试 (删除D)
    System.out.println("\n删除叶子节点 'D':");
    boolean deleted1 = biTree.deleteNode('D');
    if (deleted1) {
        System.out.println("删除成功!");
        System.out.println("删除后的树结构 (前序遍历): " + biTree.DLR3());
    }

    // 创建复杂的树来测试其他删除情况
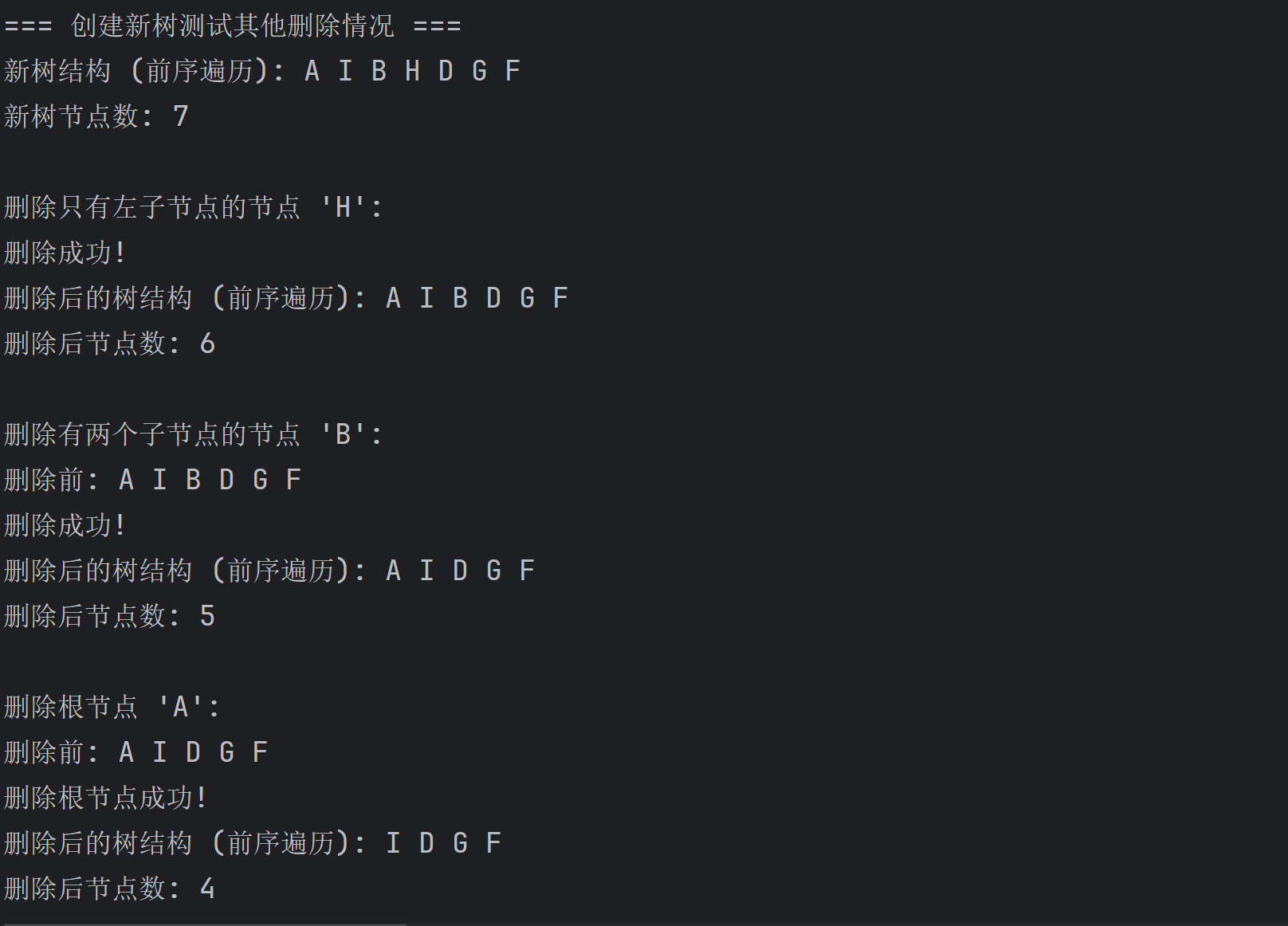
    BiTree testTree = new BiTree();
    String complexInput = "ABDF##G##H##I##E##C##";
    testTree.createBiTree(complexInput);

    // 删除有两个子节点的节点测试 (删除B)
    System.out.println("\n删除有两个子节点的节点 'B':");
    System.out.println("删除前: " + testTree.DLR3());
    boolean deleted2 = testTree.deleteNode('B');
    if (deleted2) {
        System.out.println("删除成功!");
        System.out.println("删除后的树结构 (前序遍历): " + testTree.DLR3());
    }
}

6.3 测试结果分析

运行测试程序，我们可以看到以下结果：

复制代码 
=== 二叉树查找和删除功能测试 ===
4. 查找功能测试:
递归查找: 找到节点 D
非递归查找: 找到节点 E

5. 删除节点功能测试:
删除前的树结构 (前序遍历): A B D E C

删除叶子节点 'D':
删除成功!
删除后的树结构 (前序遍历): A B E C

删除有两个子节点的节点 'B':
删除前: A I B H D G F
删除成功!
删除后的树结构 (前序遍历): A I D G F


七、性能分析与优化策略

7.1 时间复杂度分析

查找操作的时间复杂度：

  • 最好情况： O(1) - 目标节点是根节点
  • 平均情况： O(n) - 需要访问约一半的节点
  • 最坏情况： O(n) - 需要访问所有节点

删除操作的时间复杂度：

  • 查找阶段： O(n) - 需要先找到目标节点
  • 删除阶段： O(1) 到 O(h) - 取决于删除的节点类型
    • 叶子节点：O(1)
    • 单子节点：O(1)
    • 双子节点：O(h)，h为右子树的高度

7.2 空间复杂度分析

操作类型 递归实现 非递归实现
查找 O(h) - 递归栈 O(h) - 显式栈
删除 O(h) - 递归栈 + O(h) - 查找栈 O(h) - 查找栈

其中h为树的高度，最坏情况下h = n。

7.3 性能优化策略

7.3.1 查找优化
  1. 提前终止： 找到目标后立即返回，避免不必要的遍历
  2. 剪枝策略： 根据先验知识选择更可能包含目标的分支
  3. 并行查找： 对于大型树，可以考虑并行查找左右子树
7.3.2 删除优化
  1. 懒惰删除： 标记删除而不是立即删除，批量处理
  2. 节点池： 重用被删除节点的内存，减少GC压力
  3. 平衡维护： 对于特殊类型的树，删除后考虑平衡调整

7.4 内存管理考虑

在Java中，内存管理主要由垃圾收集器负责，但仍需考虑：

java 复制代码 
// 内存友好的删除示例
public boolean deleteWithMemoryManagement(char target) {
    BiTreeNode nodeToDelete = searchIterative(target);
    if (nodeToDelete == null) {
        return false;
    }

    // 执行删除操作...

    // 手动解除引用，帮助GC
    nodeToDelete.lchild = null;
    nodeToDelete.rchild = null;

    return true;
}

八、实际应用场景与扩展

8.1 实际应用场景

文件系统管理：

  • 目录结构的查找和删除
  • 文件索引的维护
  • 权限管理的实现

数据库索引：

  • B+树节点的维护
  • 查询优化器的实现
  • 事务处理的回滚操作

编译器设计：

  • 抽象语法树(AST)的构建和修改
  • 优化过程中的节点删除
  • 语法检查的实现

游戏开发：

  • 场景图的管理
  • 碰撞检测的优化
  • AI决策树的维护

8.2 与前端开发的对比

正如前面提到的，二叉树的删除操作与前端DOM操作有着惊人的相似性：

相似之处：

  1. 节点层次结构： 两者都是树形结构
  2. 父子关系维护： 删除时都需要重新建立连接
  3. 子节点处理： 都需要考虑如何处理被删除节点的子节点

代码对比示例：

javascript 复制代码 
// JavaScript DOM 删除操作
function removeDOMNode(elementId) {
    const element = document.getElementById(elementId);
    if (element) {
        const parent = element.parentNode;

        // 将子元素移动到父元素中
        while (element.firstChild) {
            parent.appendChild(element.firstChild);
        }

        parent.removeChild(element);
    }
}

这种对比体现了算法思想的普适性------良好的算法设计模式可以跨越不同的技术领域。

8.3 扩展学习方向

掌握了二叉树的查找和删除操作后，可以继续学习：

  1. 平衡二叉树（AVL树）： 自动平衡的二叉搜索树
  2. 红黑树： 广泛应用的平衡树结构
  3. B树和B+树： 数据库和文件系统的核心数据结构
  4. 堆（Heap）： 特殊的树形结构，用于优先队列
  5. 字典树（Trie树）： 字符串处理的高效数据结构

九、总结与学习建议

9.1 核心技术总结

通过本文的学习，我们掌握了：

  1. 查找算法：

    • 递归查找的简洁实现
    • 非递归查找的栈模拟技术
    • 两种方法的性能对比和选择

  2. 删除算法：

    • 四种删除情况的分类处理
    • 双子节点的复杂替换策略
    • 根节点的特殊处理机制

  3. 编程技巧：

    • 递归与迭代的转换技巧
    • 栈结构在树算法中的应用
    • 边界条件的处理方法

9.2 深度理解的关键

要真正掌握二叉树的高级操作，需要理解以下几个要点：

技术洞察1： 树的递归性质不仅体现在代码结构上，更体现在问题解决思路上。学会用递归思维思考树问题是关键。
技术洞察2： 删除操作的核心挑战在于连接关系的重新建立 ，而不仅仅是节点的移除。这体现了数据结构中关系管理的重要性。
技术洞察3： 复杂算法往往可以分解为简单的基本操作的组合。掌握基本操作是构建复杂算法的基础。

9.3 实践建议

  1. 动手实践：

    • 亲自实现所有代码，不要只是复制粘贴
    • 尝试不同的测试用例，包括边界情况
    • 用调试工具跟踪算法的执行过程

  2. 可视化学习：

    • 画出算法执行过程中树的变化
    • 使用在线算法可视化工具辅助理解
    • 制作算法流程图加深记忆

  3. 举一反三：

    • 思考如何修改算法支持其他操作（如插入、更新）
    • 尝试实现其他类型的树结构
    • 将算法应用到实际问题中

9.4 常见错误与调试技巧

常见错误：

  1. 忘记处理空树的情况
  2. 删除后没有正确更新计数器
  3. 父子节点的连接建立错误
  4. 栈的入栈顺序错误

调试技巧：

java 复制代码 
// 调试辅助方法
public void printTreeStructure() {
    System.out.println("当前树结构：");
    printTreeHelper(root, 0);
}

private void printTreeHelper(BiTreeNode node, int level) {
    if (node != null) {
        printTreeHelper(node.rchild, level + 1);
        System.out.println("  ".repeat(level) + node.data);
        printTreeHelper(node.lchild, level + 1);
    }
}

9.5 性能测试与优化建议

java 复制代码 
// 性能测试代码示例
public void performanceTest() {
    long startTime = System.nanoTime();

    // 执行大量查找操作
    for (int i = 0; i < 10000; i++) {
        searchIterative('A');
    }

    long endTime = System.nanoTime();
    System.out.println("查找操作耗时: " + (endTime - startTime) + " ns");
}

参考资源：

相关标签：
Java数据结构 二叉树操作 算法实现 查找删除 数据结构进阶

如果本文对你有帮助，别忘了点赞收藏关注！有什么问题欢迎在评论区交流讨论！

投票互动： 你认为二叉树操作中最难理解的部分是什么？

A. 递归思想的运用 B. 删除操作的四种情况 C. 栈结构的模拟 D. 性能优化技巧

相关推荐
ALex_zry2 小时前
C++20/23标准对进程间共享信息的优化：从传统IPC到现代C++的演进
开发语言·c++·c++20
Coder_Boy_2 小时前
【人工智能应用技术】-基础实战-小程序应用（基于springAI+百度语音技术）智能语音控制-单片机交互代码
java·人工智能·后端·嵌入式硬件
IMPYLH2 小时前
Lua 的 OS（操作系统） 模块
开发语言·笔记·后端·游戏引擎·lua
YGGP2 小时前
【Golang】LeetCode 287. 寻找重复数
开发语言·leetcode·golang
前端小白在前进2 小时前
力扣刷题：千位分割数
javascript·算法·leetcode
free-elcmacom2 小时前
机器学习高阶教程＜11＞当数据开始“折叠”：流形学习与深度神经网络如何发现世界的隐藏维度
人工智能·python·神经网络·学习·算法·机器学习·dnn
吴佳浩 Alben2 小时前
Go 1.22 通关讲解
开发语言·数据库·golang
黎雁·泠崖2 小时前
指针家族高阶篇：字符指针、数组指针、函数指针及转移表应用
c语言·开发语言
小年糕是糕手2 小时前
【C/C++刷题集】string类（一）
开发语言·数据结构·c++·算法·leetcode
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05BongoCat - 跨平台键盘猫动画工具06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07Labelme从安装到标注：零基础完整指南08jdk21下载、安装（Windows、Linux、macOS）09CentOS的ISO镜像下载10Open-AutoGLM Windows 安装部署教程