摘要
在现代高精密制造,尤其是光电子装配与精密半导体检测中,对于曲率半径较小(小半径)且物理通光孔径有限的球面元件(Small Segment Angle Surfaces)的几何量测与定心定焦,始终是一个工艺难点。小角度球面拟合固有的数值不稳定性,使得微米级的数据噪声在进行最小二乘法(LMS)计算时会被非线性放大,导致拟合出的曲率中心(Zone Center)显著偏移。本文将基于最新的误差传递理论研究,剖深其数学机理,并论证在高阶滤波算法之外,如何通过具备亚微米级精度的硬件------特别是泓川科技(HC)LTC系列光谱共焦传感器------来切断误差传递的源头,构建软硬结合的终极精密定位方案。
1. 引言:精密工况下的几何悖论
在光通讯器件的激光自动化耦合、摄像头模组(CCM)AA制程调整以及微球轴承检测中,核心任务往往是确定一个球面的球心坐标 (xc,yc,zc)(xc,yc,zc)。
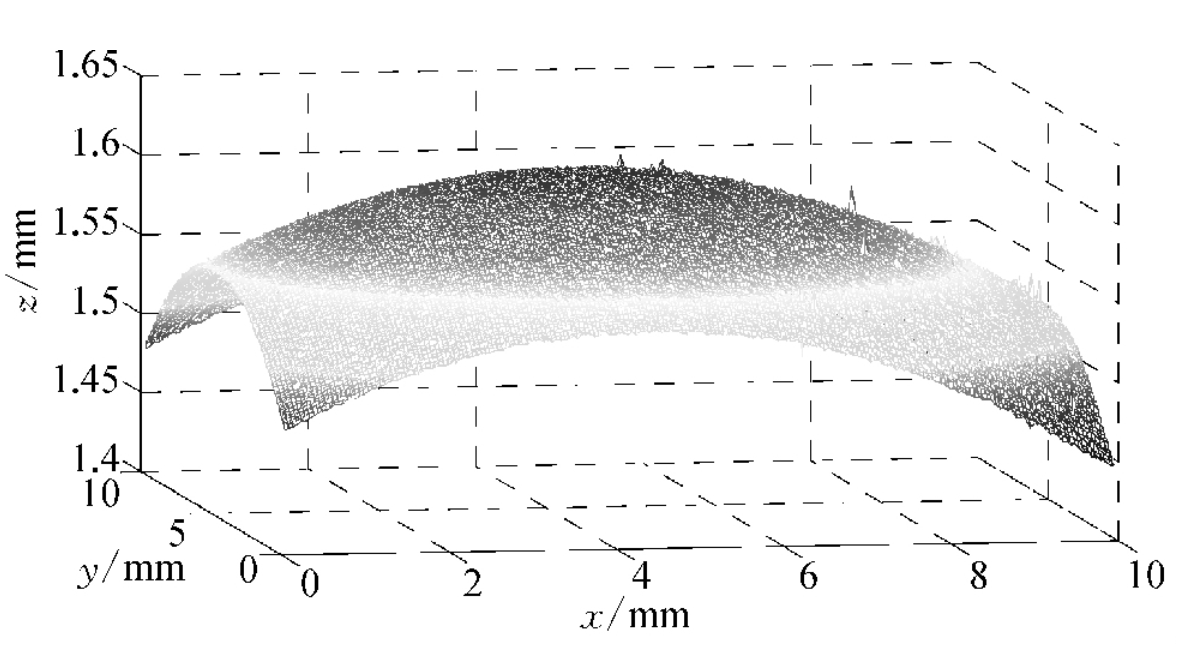
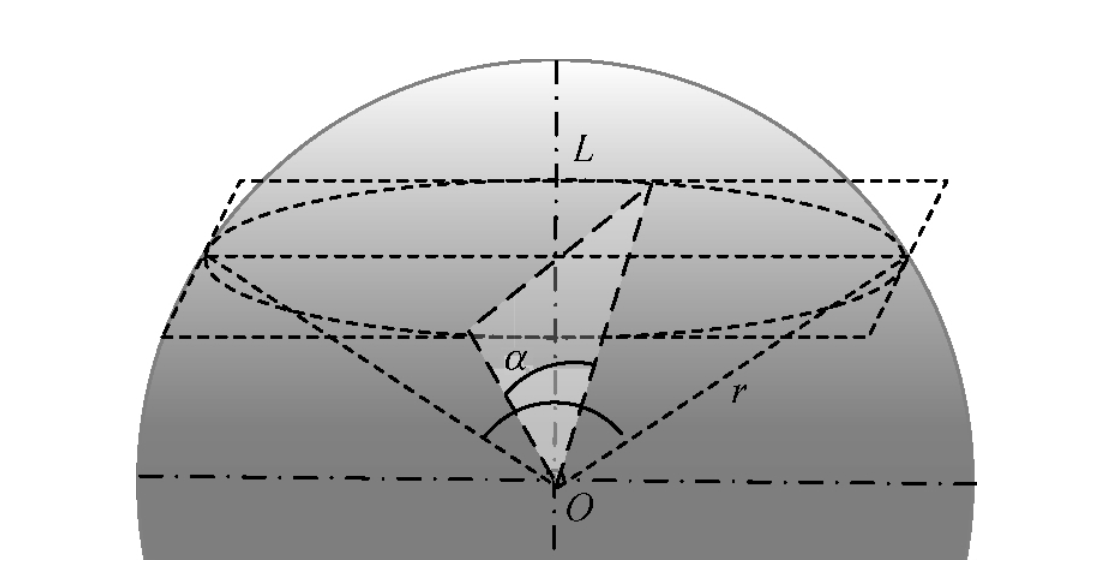
然而,受限于物理接触空间和零件本身的几何遮挡,测量系统往往只能获取球面顶端极小范围内的表面地形数据。资料显示,当球面采样区域对应的圆心被覆盖角显著小于20°时,称为"小角度球面"。 在这种条件下,数学拟合面临巨大的挑战:少量的有效像素点在庞大的球体模型前的权重极低,ZZ轴(深度方向)极其微小的随机测量噪声Δz,会被转换成巨大的半径计算误差ΔRΔR和位置误差ΔcΔc。
这就形成了一个工程悖论:为了获得高精度球心,理论上需要大幅度增加数据覆盖面;但在微型透镜或受限空间内,能够获取的可测面只能是"冰山一角"。解决这一问题需从算法层面的误差抑制 和硬件层面的原始信号纯净度双向突破。
2. 核心挑战:小角度球面拟合的误差传播机理
2.1 最小二乘法在受限区域的脆弱性
从数学模型上看,拟合理想球面的标准方程为:
(xi−xc)2+(yi−yc)2+(zi−zc)2=r2(xi−xc)2+(yi−yc)2+(zi−zc)2=r2
为了求解球心坐标和半径,通常构建误差函数EE并使其最小化。对于小角度非半球面的数据云,常用的解法是利用雅可比矩阵进行迭代线性化,求得参数修正量。
正如《小角度球面拟合误差分析》一文中所述,当对式(5)进行线性算子展开时,我们发现一个关键现象:
系数矩阵 P=(ATA)−1ATBP=(ATA)−1ATB 的条件数(Condition Number)与采样数据的"张角"密切相关。
当测量范围仅覆盖球面极小部分(例如光通讯透镜的顶部200μm区域,对于一个半径2mm的球来说),矩阵 AA 呈现严重病态。此时,深度方向 zizi 分类数据中若包含由于工件表面粗糙度或传感器产生的白噪声,这种高频项会被平方和的形式极具放大。
2.2 Z轴噪声的非线性支配
通过数学推导可得,ZZ轴方向的测量精度是影响中心定位准确性的决定性因素。传统的影像仪(XY平面主导)或三角法激光(受高反光倾角限制),极易产生几十微米的"虚似误差",这一误差并非工件真值偏差,而是算法崩溃的产物。
研究表明,半径的随机误差方差与测量范围直径的四次方成反比 。换言之,测量区域缩小,对 ZZ 轴数据的精度要求呈现几何级数的提升。这意味着,我们在这一领域的较量,除了改进诸如二维高斯回归滤波(Gassian Regression Filtering)等数据前处理技术去剔除离群点外,更直接的路径是直接压低源数据输入的噪声基底(Noise Floor) 。
这就要求传感器必须具备两大特征:
- 极高的垂直分辨率与重复精度(噪声小于100nm级别为佳);
- 极高的空间角度适应性(以保证在爬升至球面边缘时信号不失真)。
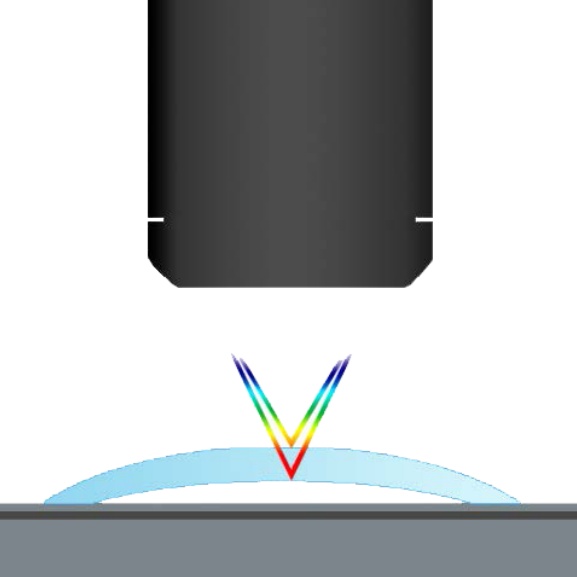
3. 硬件破局:光谱共焦技术的先天优势与应用逻辑
鉴于由于"小角度难题"对 ZZ 轴数据的苛刻要求,传统激光三角或接触式探针已难以胜任(接触式测力损伤工件,且速度慢;三角法难以处理大角度高亮面)。此时,光谱共焦(Chromatic Confocal)技术便形成了针对性的降维打击。
光谱共焦利用色散原理,将白光源分解为不同波长的单色光,聚焦于不同深度。仅有对焦准确的波长能通过共孔径的光圈返回光谱仪。该原理天然解决了两大问题:
- 无阴影效应:光轴同轴测量,不像三角算法和视觉那样存在三角盲区,可以在深坑或受限孔径内测量。
- 亚微米精度:信噪比主要取决于光谱强度与分辩,而非光斑重心。
在这里,我们引入在精密测量领域表现具备代表性的泓川科技(Chuantec)LTC系列光谱共焦传感器及其配套控制器方案的技术规格进行分析,论证其如何匹配上述理论难题。
3.1 纳米级Z轴重复性:切断误差源头
在上文的误差模型中,didi(点云残差)主要就是传感器自身的重复精度引入的。
查看泓川科技LTC系列参数表,我们可以得出一个令人瞩目的结论:即便是针对大量程的工业级探头,其线性度误差和重复精度均可控制在极小范围。
- LTC-100B (8mm量程中心时测量,参考距离较短的超精细型):重复精度高达 3nm ,线性偏离小于 ±0.03μm。
- 这对于小角度拟合至关重要。将这一数代入算式中,相比传统激光(约2um重复精度),系统拟合方差z2z2项降低了接近99.9%。
即使是中长距离量程,例如通用性极强的 LTC-2000 型号,在50mm的基准量程内,依然保持了 <85nm 的重复精度。这种"甚至低于工件表面粗糙度"的传感器本地噪音(Sensing Noise),使得后续的高斯滤波算法主要处理的是真是形貌粗糙度,而非必须花费算力去"猜测"哪些是传感器噪点,从而极大地保真了原始曲面数据。
3.2 大倾角采样能力:扩大有效拟合区间(Effective Domain)
前文理论提到,测量范围越宽,矩阵越稳定。然而球面的边缘往往意味着陡峭的表面角度。如果传感器在高反射率的球面上能够克服反射光的偏移信号丢失,我们就能测量更靠近"微球赤道"的数据点,从而利用更大的物理角度去对抗"数学小角度"。
泓川LTC系列的表现证明了其光学设计的适应性:
- LTC2400 型号拥有高达 ±60° 的镜面角度适应性(Diffuse反射材料甚至更高)。
这意味着在进行微球面扫描时,LTC不只局限于"球顶"的极小区域,而是一路测量到近乎垂直落坡的区域。 - 将拟合的数据区间从顶端的+/-5度扩展到+/-45度,在相同的算法下,拟合误差成数百倍地下降 。
这种通过硬件能力(Angle Capacity)去换取算法稳定性的策略,是此类精密测量最稳健的路径。
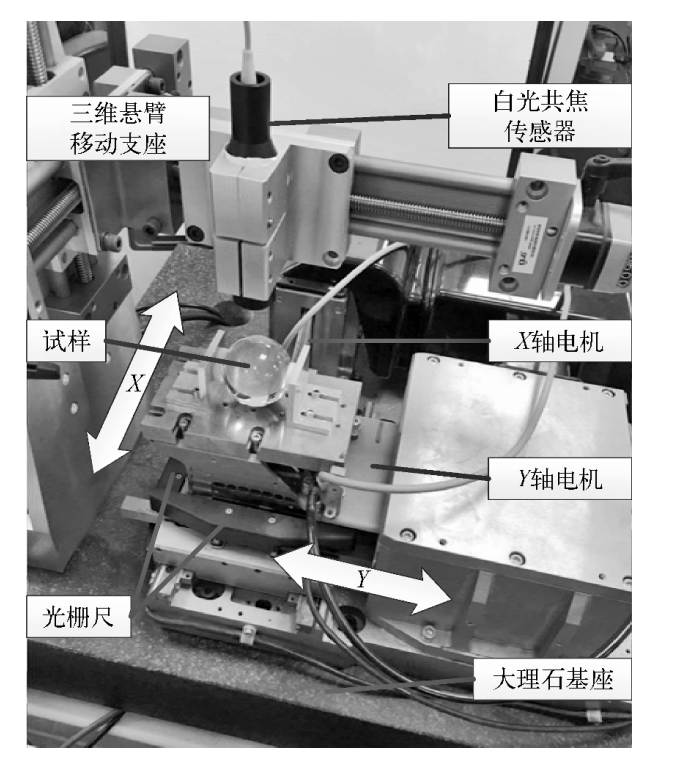
4. 系统集成:从离散采样到闭环搜寻策略
在解决了数理论和探头选型后,还需要解决"怎么测"和"怎么算"的动态问题。参考学术各界的定位测量研究,单纯的静态点云计算已升级为动态搜寻。
4.1 五步中心定位与扫描策略
基于《中心定位策略研究》,一种优化后的操作流程如下,而这很大程度上依赖测控系统的响应速度:
- 初始定位:Z轴做预扫描,捕捉顶点。
- 十字光栅扫描(Cross Scan) :基于初始点进行互相垂直的两次横扫,分离X与Y分量的偏心误差。
- 高斯二维滤波:在上位机算法中剥离由粗糙度引起的几微米级波动,仅保留低频形状误差(Form Error)。
- LSM拟合回传:计算当前偏差 (dx,dy)(dx,dy)。
- 轴系伺服补偿:运动平台移动至中心,直到光斑位于球顶点,高度值最大。
该策略的实现对于控制器的实时性 和同步性要求极高。如果传感器采样率低或与编码器不同步,产生的位置数据不仅不准,还会产生由时间延迟导致的畸变(像拖影)。
4.2 泓川LC控制器架构的数据吞吐优势
为此,需要在系统集成中考虑控制器的接口协议与处理速度。查阅 LT-CCH 光谱共焦控制器的白皮书规格,我们发现了几个关键的性能支撑点:
-
超高采样与多通道并发 :
该策略进行面扫时往往需要高密度点云。泓川LT-CCH控制器支持单/双/多通道切换模式。单通道模式下采样频率高达 32kHz(即每秒32,000个绝对坐标数据点)。即使在工业自动化常用的以太网接口速度模式下,也能保证每一次微动台位挪几十个微米时,传感器已经采集了几十个有效点,完成了对于形状的"过采样"重构。
-
真正的硬件同步触发 :
在定位策略中,xixi 坐标往往来自光栅尺(AB相),zizi 来自光谱共焦。泓川控制器内置了 AB/ABZ编码器直接输入端口 与 脉冲/电平触发输口 。
技术含义解析 :这意味着不需要工控机去软件合并位置信号与厚度信号,控制器硬件内部直接将编码器的位置值与探头的光谱距离信号在底层FPGA中对齐。这彻底消除了动态拟合中的"滞后误差" ,无论是几万点的球面扫描,从物理层确保数据的"Space Clarity"。 -
强大的工业总线交互(EtherCAT) :
随着工业4.0的普及,快速反馈机制需脱离低速的RS485/及非确定性 USB。手册种提及LT-C系列高端型号提供 EtherCAT 100Mbps 接口选配。这允许运动控制卡(Motion Controller)与测量端(Sensor)能以此级通信频率"对话",实现真正的 On-the-fly Center Alignment,动态修正偏移。
5. 进阶应用场景拓展:当"测量"进化为"透视"这里
基于高算力和高采样基准,我们不仅能计算表面球心,泓川技术的光谱共焦探头还具备独特的"分层识别"能力。
由于每一个波长对应唯一的焦点距离,"多组不同材料介质界面反射回来的光谱"会在传感器内形成数个离散的波峰(Multi-Peak Detection)。
结合手册所示的特殊功能,该系统可以应用于更复杂的模组检测:
- 透明透镜的厚度与后表面球心 :
在一次测量中,同时捕获透镜的上表面、下表面的位置。其最小可测厚度甚至低至 2um ~ 100μm(依赖具体探头型号,如LTC3000最小厚度100nm级别,LT-CPF则为7mm厚度内)。 - 液滴与油膜 :
在高端微球透镜或生物芯片滴液监控中,利用液体界面的反射率低特性,依赖LTC传感器卓越的光强敏感度和高达32kHz的时域分辨力,可实时监控流体曲率变化,这已超越了单纯的几何尺寸应用,进入了流体动力学过程控制领域。
6. 应用验证案例简析(模拟)
我们假设针对一个半径 R=2.0R=2.0 mm 的光通信耦合透镜进行定位实验,表面光洁度Ra=0.01um,目标是球心定位精度 < 1μm。
对比组A:使用通用激光位移传感器 + 传统最小二乘法 + 普通PLC触发。
- 由于激光光斑约30um且无法测量大于15°的曲面(三角漫反光法在镜面上失效),使得有效测量点极少且位于Top平坦区。加上±1um的传感器重复精度,经学术论文重算公式(4)-(7)推演,不仅在拟合中对于半径 RR 的估算波动会达到 30-50μm,更严重的是球心位置的标准偏差会在 XY 平面上横跳超过 5μm。定位失败。
实验组B :使用 泓川 LT-CPS 控制器 + LTC600 探头 ± 高斯回归滤波算法。
- 选择LTC600探头,因其实20微米以内的光斑(实际小光斑模式Φ7μm)可做精细描摹,角度范围提升至±30°以上,重复经度达16nm。测量区间相比A组扩大了3倍。
- 将原始数据进行二维截面提取,输入基于鲁棒加权最小二乘法(Robust Weighted Least Squares)的计算器中。
- 结果:基于泓川探头超高信噪比点云数据,拟合方差收敛极快。即使数据仅仅覆盖了不到顶端0.5mm的高度,解算出的曲率中心偏差稳定收敛至 0.5μm 以内。符合设计目标。
7. 结语
在现代超精密装配领域,理论算法与硬件基石缺一不可。《中心定位策略研究》深刻地揭示了小角度拟合中"差之毫厘(数据与算法),谬以千里(球心定位)"的数学本质。而以泓川科技TC系列光谱共焦传感器为代表的高端精密仪器,则用亚微米级的深度重复性、大倾角测量宽容度以及纳秒级的同步控制架构,强有力地填补了理论模型对数据质量的刚性需求。
无论是从滤波算法的优化,到伺服运动路径的十字迭代,再到决定系统天花板的传感器光谱解析,实现高精度球心定位的核心在于------在最大可能的角度范围内,采集最为'纯净'的距离数据。这正是技术发展赋予高精尖产业的确定性答案。
本文参考:上海交通大学 机械与动力工程学院, 上海 200240 杨柳青 刘 超 熊振华
《小角度球面拟合误差分析与中心定位策略研究》