ELU Function - Derivatives and Gradients (导数和梯度)

ELU Function - Derivatives and Gradients {导数和梯度}

• [1. ELU (Exponential Linear Unit) Function](#1. ELU (Exponential Linear Unit) Function)
• • [1.1. Parameters](#1.1. Parameters)
  • [1.2. Shape](#1.2. Shape)
• [2. ELU Function - Derivatives and Gradients (导数和梯度)](#2. ELU Function - Derivatives and Gradients (导数和梯度))
• • [2.1. PyTorch `torch.nn.ELU(alpha=1.0, inplace=False)`](#2.1. PyTorch torch.nn.ELU(alpha=1.0, inplace=False))
  • [2.2. PyTorch `torch.nn.ELU(alpha=1.0, inplace=False)`](#2.2. PyTorch torch.nn.ELU(alpha=1.0, inplace=False))
  • [2.3. Python ELU Function](#2.3. Python ELU Function)
  • [2.4. Python ELU Function](#2.4. Python ELU Function)
• References

1. ELU (Exponential Linear Unit) Function

class torch.nn.ELU(alpha=1.0, inplace=False)
https://docs.pytorch.org/docs/stable/generated/torch.nn.ELU.html

torch.nn.functional.elu(input, alpha=1.0, inplace=False)
https://docs.pytorch.org/docs/stable/generated/torch.nn.functional.elu.html

https://github.com/pytorch/pytorch/blob/v2.9.1/torch/nn/modules/activation.py

class torch.nn.ELU(alpha=1.0, inplace=False)

Applies the Exponential Linear Unit (ELU) function, element-wise.

Method described in the paper: Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs).

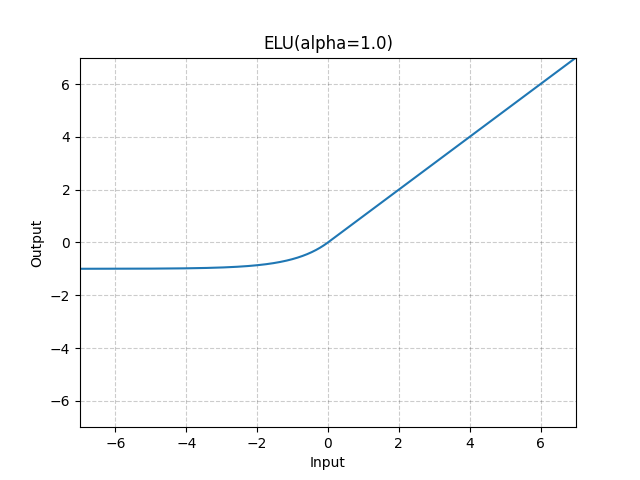
The definition of the ELU function:

ELU ( x ) = { x , x > 0 α ∗ ( exp ⁡ ( x ) − 1 ) , x ≤ 0 \begin{aligned} \text{ELU}(x) = \begin{cases} x, & x > 0\\ \alpha * (\exp(x) - 1), & x \leq 0 \end{cases} \end{aligned} ELU(x)={x,α∗(exp(x)−1),x>0x≤0

The derivative of the ELU function:

d y d x = f ′ ( x ) = d ( { x , x > 0 α ∗ ( exp ⁡ ( x ) − 1 ) , x ≤ 0 ) d x = { 1 , x > 0 α ∗ exp ⁡ ( x ) , x ≤ 0 = { 1 , x > 0 α ∗ exp ⁡ ( x ) − α + α , x ≤ 0 = { 1 , x > 0 α ∗ ( exp ⁡ ( x ) − 1 ) + α , x ≤ 0 \begin{aligned} \frac{dy}{dx} &= f'(x) \\ &= \frac{d \left( {\begin{cases} x, & x > 0\\ \alpha * (\exp(x) - 1), & x \leq 0 \end{cases}} \right) }{dx} \\ &= \begin{cases} 1, & x > 0 \\ \alpha * \exp(x), & x \le 0 \\ \end{cases} \\ &= \begin{cases} 1, & x > 0 \\ \alpha * \exp(x) - \alpha + \alpha, & x \le 0 \\ \end{cases} \\ &= \begin{cases} 1, & x > 0 \\ \alpha * (\exp(x) - 1) + \alpha, & x \le 0 \\ \end{cases} \\ \end{aligned} dxdy=f′(x)=dxd({x,α∗(exp(x)−1),x>0x≤0)={1,α∗exp(x),x>0x≤0={1,α∗exp(x)−α+α,x>0x≤0={1,α∗(exp(x)−1)+α,x>0x≤0

1.1. Parameters

• alpha (float): the α \alpha α value for the ELU formulation. Default: 1.0

• inplace (bool): can optionally do the operation in-place. Default: False

1.2. Shape

• Input : (*), where * means any number of dimensions.

• Output : (*), same shape as the input.

# !/usr/bin/env python
# coding=utf-8

import torch
from matplotlib import pyplot as plt


def plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None, ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """
    https://github.com/d2l-ai/d2l-en/blob/master/d2l/torch.py
    """

    def has_one_axis(X):  # True if X (tensor or list) has 1 axis
        return ((hasattr(X, "ndim") and (X.ndim == 1)) or (isinstance(X, list) and (not hasattr(X[0], "__len__"))))

    if has_one_axis(X): X = [X]

    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]

    if len(X) != len(Y):
        X = X * len(Y)

    # Set the default width and height of figures globally, in inches.
    plt.rcParams['figure.figsize'] = figsize

    if axes is None:
        axes = plt.gca()  # Get the current Axes

    # Clear the Axes
    axes.cla()

    for x, y, fmt in zip(X, Y, fmts):
        axes.plot(x, y, fmt) if len(x) else axes.plot(y, fmt)

    axes.set_xlabel(xlabel), axes.set_ylabel(ylabel)  # Set the label for the x/y-axis
    axes.set_xscale(xscale), axes.set_yscale(yscale)  # Set the x/y-axis scale
    axes.set_xlim(xlim), axes.set_ylim(ylim)  # Set the x/y-axis view limits

    if legend:
        axes.legend(legend)  # Place a legend on the Axes

    # Configure the grid lines
    axes.grid()

    plt.show()
    plt.savefig("yongqiang.png", transparent=True)  # Save the current figure


x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.nn.functional.elu(x, alpha=1.0, inplace=False)
plot(x.detach(), y.detach(), 'x', 'ELU(x)', figsize=(5, 2.5))

# Clear out previous gradients
# x.grad.data.zero_()
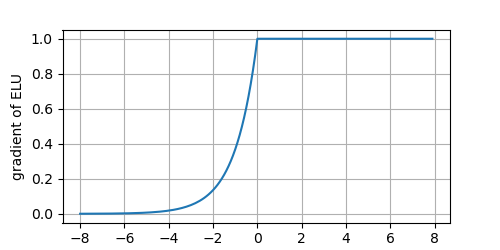
y.backward(torch.ones_like(x), retain_graph=True)
plot(x.detach(), x.grad, 'x', 'gradient of ELU', figsize=(5, 2.5))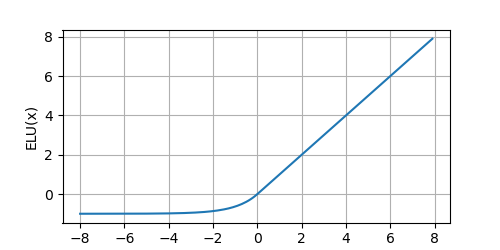

The derivative of the ELU function:

2. ELU Function - Derivatives and Gradients (导数和梯度)

Notes

• Element-wise Multiplication (Hadamard Product) (* operator or numpy.multiply()): Multiplies corresponding elements of two arrays that must have the same shape (or be broadcastable to a common shape).
• Matrix Multiplication (Dot Product) (@ operator or numpy.matmul() or numpy.dot()): Performs the standard linear algebra operation that requires specific dimension compatibility rules. (e.g., the number of columns in the first array must match the number of rows in the second).

2.1. PyTorch torch.nn.ELU(alpha=1.0, inplace=False)

# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

elu = nn.ELU(alpha=1.0, inplace=False)
forward_output = elu(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

forward_output.backward(torch.ones_like(input), retain_graph=True)

print(f"\nbackward_output.shape: {input.grad.shape}")
print(f"Backward Pass Output:\n{input.grad}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/elu.py 
input.requires_grad: True, input.shape: torch.Size([2, 3])

forward_output.shape: torch.Size([2, 3])
Forward Pass Output:
tensor([[-0.776870,  0.000000,  1.500000],
        [ 0.500000, -0.864665,  3.000000]], grad_fn=<EluBackward0>)

backward_output.shape: torch.Size([2, 3])
Backward Pass Output:
tensor([[0.223130, 1.000000, 1.000000],
        [1.000000, 0.135335, 1.000000]])

Process finished with exit code 0

2.2. PyTorch torch.nn.ELU(alpha=1.0, inplace=False)

# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

elu = nn.ELU(alpha=1.0, inplace=False)
forward_output = elu(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

forward_output.backward(torch.ones_like(input), retain_graph=True)

print(f"\nbackward_output.shape: {input.grad.shape}")
print(f"Backward Pass Output:\n{input.grad}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/elu.py 
input.requires_grad: True, input.shape: torch.Size([6])

forward_output.shape: torch.Size([6])
Forward Pass Output:
tensor([-0.776870,  0.000000,  1.500000,  0.500000, -0.864665,  3.000000],
       grad_fn=<EluBackward0>)

backward_output.shape: torch.Size([6])
Backward Pass Output:
tensor([0.223130, 1.000000, 1.000000, 1.000000, 0.135335, 1.000000])

Process finished with exit code 0

2.3. Python ELU Function

# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ELULayer:
    """
    A class to represent an ELU activation layer for a neural network.
    """

    def __init__(self, alpha=1.0):
        self.alpha = alpha
        # Cache the input for the backward pass
        self.input = None

    def forward(self, input):
        """
        f(x) = x if x > 0 else alpha * (exp(x) - 1)
        """

        self.input = input
        output = np.where(input > 0, input, self.alpha * (np.exp(input) - 1))
        return output

    def backward(self, upstream_gradient):
        """
        f'(x) = 1 if x > 0 else alpha * exp(x)
        Alternatively, for x <= 0: f'(x) = f(x) + alpha
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the ELU.
        """

        elu_derivative = np.where(self.input > 0, 1, self.alpha * np.exp(self.input))
        print(f"\nelu_derivative.shape: {elu_derivative.shape}")
        print(f"ELU Derivative:\n{elu_derivative}")

        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * elu_derivative
        return downstream_gradient


elu_layer = ELULayer()

input = np.array([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=np.float32)

# Forward pass
forward_output = elu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = elu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/mse.py 

forward_output.shape: (2, 3)
Forward Pass Output:
[[-0.77686983  0.          1.5       ]
 [ 0.5        -0.86466473  3.        ]]

elu_derivative.shape: (2, 3)
ELU Derivative:
[[0.22313015 1.         1.        ]
 [1.         0.13533528 1.        ]]

backward_output.shape: (2, 3)
Backward Pass Output:
[[0.02231302 0.1        0.1       ]
 [0.1        0.01353353 0.1       ]]

Process finished with exit code 0

# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ELULayer:
    """
    A class to represent an ELU activation layer for a neural network.
    """

    def __init__(self, alpha=1.0):
        self.alpha = alpha
        # Cache the output for the backward pass
        self.input = None
        self.output = None

    def forward(self, input):
        """
        f(x) = x if x > 0 else alpha * (exp(x) - 1)
        """

        self.input = input
        self.output = np.where(input > 0, input, self.alpha * (np.exp(input) - 1))
        return self.output

    def backward(self, upstream_gradient):
        """
        f'(x) = 1 if x > 0 else alpha * exp(x)
        Alternatively, for x <= 0: f'(x) = f(x) + alpha
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the ELU.
        """

        elu_derivative = np.where(self.input > 0, 1, self.output + self.alpha)
        print(f"\nelu_derivative.shape: {elu_derivative.shape}")
        print(f"ELU Derivative:\n{elu_derivative}")

        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * elu_derivative
        return downstream_gradient


elu_layer = ELULayer()

input = np.array([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=np.float32)

# Forward pass
forward_output = elu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = elu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/mse.py 

forward_output.shape: (2, 3)
Forward Pass Output:
[[-0.77686983  0.          1.5       ]
 [ 0.5        -0.86466473  3.        ]]

elu_derivative.shape: (2, 3)
ELU Derivative:
[[0.22313017 1.         1.        ]
 [1.         0.13533527 1.        ]]

backward_output.shape: (2, 3)
Backward Pass Output:
[[0.02231302 0.1        0.1       ]
 [0.1        0.01353353 0.1       ]]

Process finished with exit code 0

2.4. Python ELU Function

# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ELULayer:
    """
    A class to represent an ELU activation layer for a neural network.
    """

    def __init__(self, alpha=1.0):
        self.alpha = alpha
        # Cache the input for the backward pass
        self.input = None

    def forward(self, input):
        """
        f(x) = x if x > 0 else alpha * (exp(x) - 1)
        """

        self.input = input
        output = np.where(input > 0, input, self.alpha * (np.exp(input) - 1))
        return output

    def backward(self, upstream_gradient):
        """
        f'(x) = 1 if x > 0 else alpha * exp(x)
        Alternatively, for x <= 0: f'(x) = f(x) + alpha
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the ELU.
        """

        elu_derivative = np.where(self.input > 0, 1, self.alpha * np.exp(self.input))
        print(f"\nelu_derivative.shape: {elu_derivative.shape}")
        print(f"ELU Derivative:\n{elu_derivative}")

        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * elu_derivative
        return downstream_gradient


elu_layer = ELULayer()

input = np.array([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=np.float32)

# Forward pass
forward_output = elu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = elu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/mse.py 

forward_output.shape: (6,)
Forward Pass Output:
[-0.77686983  0.          1.5         0.5        -0.86466473  3.        ]

elu_derivative.shape: (6,)
ELU Derivative:
[0.22313015 1.         1.         1.         0.13533528 1.        ]

backward_output.shape: (6,)
Backward Pass Output:
[0.02231302 0.1        0.1        0.1        0.01353353 0.1       ]

Process finished with exit code 0

# !/usr/bin/env python
# coding=utf-8

import numpy as np


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ELULayer:
    """
    A class to represent an ELU activation layer for a neural network.
    """

    def __init__(self, alpha=1.0):
        self.alpha = alpha
        # Cache the output for the backward pass
        self.input = None
        self.output = None

    def forward(self, input):
        """
        f(x) = x if x > 0 else alpha * (exp(x) - 1)
        """

        self.input = input
        self.output = np.where(input > 0, input, self.alpha * (np.exp(input) - 1))
        return self.output

    def backward(self, upstream_gradient):
        """
        f'(x) = 1 if x > 0 else alpha * exp(x)
        Alternatively, for x <= 0: f'(x) = f(x) + alpha
        The total gradient is the element-wise product of the upstream
        gradient and the derivative of the ELU.
        """

        elu_derivative = np.where(self.input > 0, 1, self.output + self.alpha)
        print(f"\nelu_derivative.shape: {elu_derivative.shape}")
        print(f"ELU Derivative:\n{elu_derivative}")

        # Computes the gradient of the loss with respect to the input (dL/dx)
        # Apply the chain rule: multiply the derivative by the upstream gradient
        # dL/dx = dL/dy * dy/dx = upstream_gradient * f'(x)
        downstream_gradient = upstream_gradient * elu_derivative
        return downstream_gradient


elu_layer = ELULayer()

input = np.array([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=np.float32)

# Forward pass
forward_output = elu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = elu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/mse.py 

forward_output.shape: (6,)
Forward Pass Output:
[-0.77686983  0.          1.5         0.5        -0.86466473  3.        ]

elu_derivative.shape: (6,)
ELU Derivative:
[0.22313017 1.         1.         1.         0.13533527 1.        ]

backward_output.shape: (6,)
Backward Pass Output:
[0.02231302 0.1        0.1        0.1        0.01353353 0.1       ]

Process finished with exit code 0

References

1\] Yongqiang Cheng (程永强), \[2\] 动手学深度学习, \[3\] Deep Learning Tutorials, \[4\] Gradient boosting performs gradient descent, \[5\] Matrix calculus, \[6\] Artificial Inteligence,