深度学习3:理解神经网络

本文章知识来源于《深度学习入门》 (鱼书)，特此声明。可以当做读数笔记来进行阅读。

一、什么是神经网络？（Neural Network）

灵感来自人脑，脑由 billions（上百亿）个神经元组成，它们通过突触互相连接，传递信号。

当你看到一只猫，大脑的视觉神经元会一层层处理：从边缘 → 形状 → 耳朵/眼睛 → "这是一只猫！"

人工神经网络就是模仿这个过程的数学模型。

下图中，左侧为生物神经网络，右侧为人工神经网络

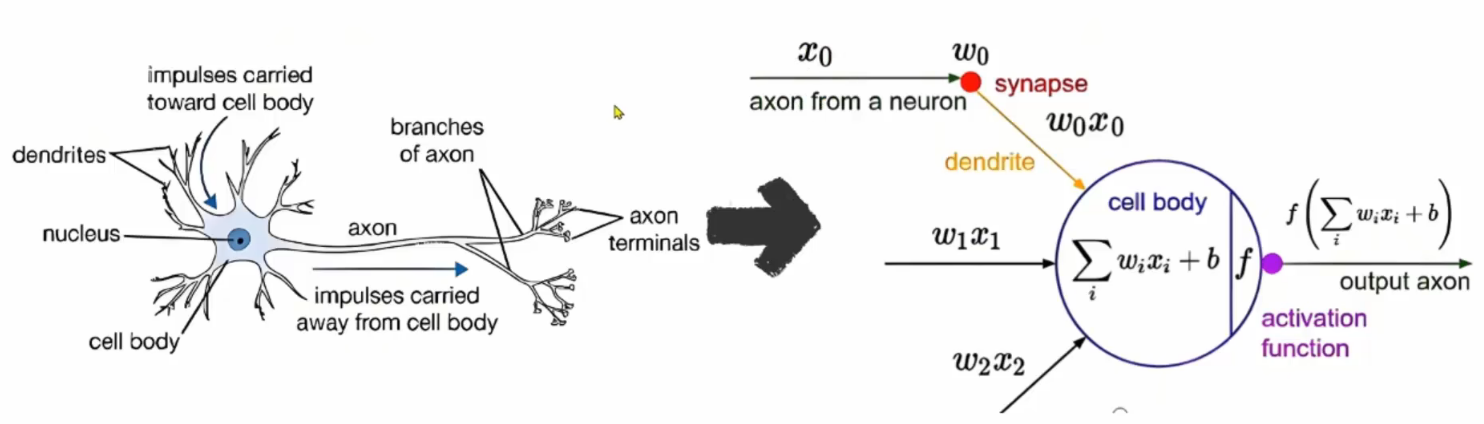
神经网络的比喻：

假设你在开一家天气预测工厂：

输入：今天的湿度、温度、风速（这些是"原料"）
工人：每一层神经元就像一排工人，他们用"加权公式"（比如：3×温度 + 2×湿度）算出一个中间判断
激活函数：每个工人下班前会拍一下"决策按钮"------比如只有当数值>0才说"要下雨！"（这就是ReLU）
输出：最后一排工人投票，决定"晴天/雨天"
训练：如果预测错了，就回溯每个工人的"权重"，微调一点点（这就是反向传播）

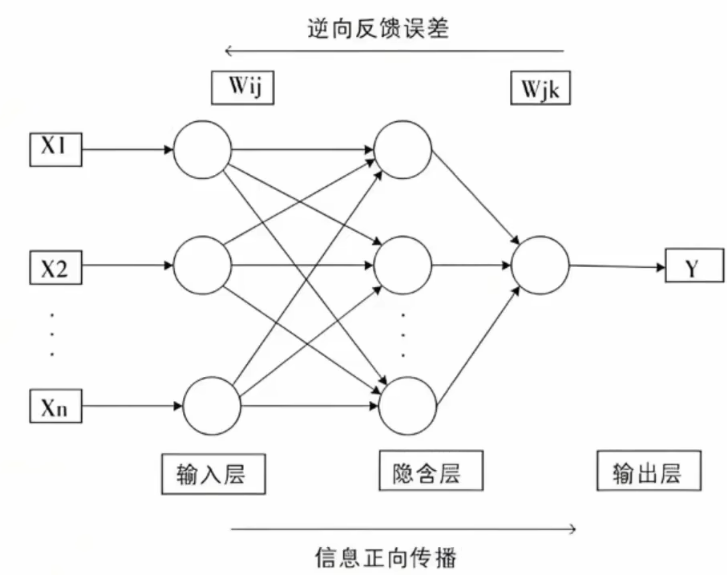
神经网络的形状类似上一章的感知机。实际上，就神经元的连接方式而言，与上一章的感知机并没有任何差异。

2.1 感知机

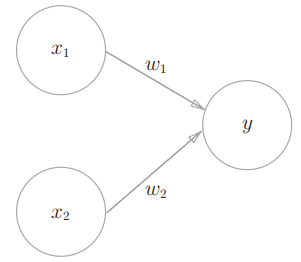
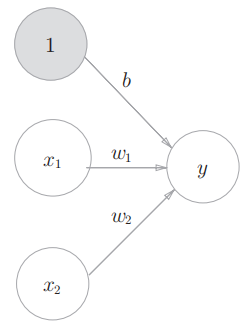
感知机接收_x_1和_x_2两个输入信号，输出_y，_果用数学式来表示图中的感知机：

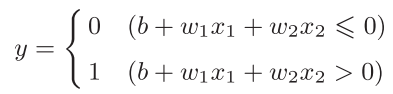
_b_是被称为偏置的参数，用于控制神经元被激活的容易程度；
而_w_1和_w_2 是表示各个信号的权重的参数，用于控制各个信号的重要性。

将上面的数学式写的更简洁一点，即引入新函数 h(x):

输入信号的总和会被函数_h_(x)转换，转换后的值就是输出_y_

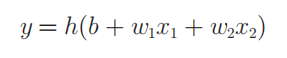
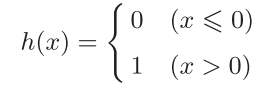
2.2 激活函数

h （x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。如"激活"一词所示，激活函数的作用在于决定如何来激活输入信号的总和。

shell 复制代码

# 计算加权输入信号和编制的总和
a=b+w1*x1+w2*x2

# 用h()函数将a转换为输出y
y=h(a)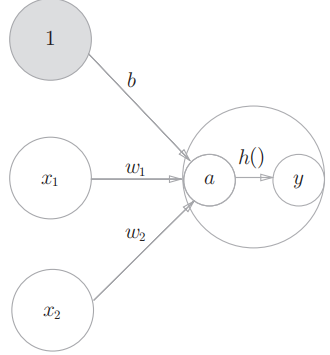

激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为"阶跃函数"。

如果将激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界了

2.2.1 sigmoid函数

神经网络中经常使用的一个激活函数就是式表示的sigmoid函数（sigmoid function）：

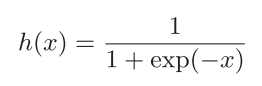
神经网络中用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。

2.2.2 对比阶跃函数

阶跃函数python实现：

python 复制代码

def step_function(x):
    if x>0:
        return 1
    else:
        return 0

上面参数x 类型只能是浮点数，稍微修改一下让它能够支持NumPy数组:

python 复制代码

def step_function(x):
    """
    阶跃函数
    :param x:
    :return:
    """
    return np.array(x > 0, dtype=np.int16)

def plot_step_function(gs):
    """
    绘制阶跃函数
    """
    ax = fig.add_subplot(gs[0, 0])
    x=np.arange(-6, 6, 0.1)
    y = step_function(x)
    ax.plot(x, y, 'b-', linewidth=2, label='y = step_function(x)')
    # 是matplotlib中用于绘制水平线的方法
    # y=0: 水平线的y坐标位置，在这里是在y=0的位置，即x轴位置
    # color='k': 线条颜色，'k'表示黑色（black）
    # linewidth=0.5: 线条宽度为0.5个像素
    # alpha=0.5: 线条透明度，0.5表示半透明
    ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
    ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
    # 标题
    ax.set_title('阶跃函数', fontsize=14, fontweight='bold')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_xlim(-5, 5)
    ax.set_ylim(-2, 2)
    # 为图表添加网格线：
    ax.grid(True, alpha=0.3)
    # 显示图例，用于标识图表中的不同数据系列 指定图例显示在图表的左上角位置
    ax.legend(loc='upper left')
    # 设置坐标轴的纵横比 'equal' 表示x轴和y轴的比例相等，即单位长度相同
    # adjustable='box' 表示通过调整坐标轴的边界框来保持比例
    ax.set_aspect('equal', adjustable='box')

python 复制代码

def sigmoid_function(x):
    """
    Sigmoid 激活函数
    :param x:
    :return:
    """
    return 1 / (1 + np.exp(-x))


def plot_sigmoid_function(gs):
    """
    绘制Sigmoid 激活函数
    """
    ax = fig.add_subplot(gs[1, 0])
    x=np.arange(-6, 6, 0.1)
    y = sigmoid_function(x)
    ax.plot(x, y, 'r-', linewidth=2, label='y = sigmoid_function(x)')
    ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
    ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
    # 标题
    ax.set_title('Sigmoid 激活函数', fontsize=14, fontweight='bold')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_xlim(-5, 5)
    ax.set_ylim(-2, 2)
    # 为图表添加网格线：
    ax.grid(True, alpha=0.3)
    # 显示图例，用于标识图表中的不同数据系列 指定图例显示在图表的左上角位置
    ax.legend(loc='upper left')
    # 设置坐标轴的纵横比 'equal' 表示x轴和y轴的比例相等，即单位长度相同
    # adjustable='box' 表示通过调整坐标轴的边界框来保持比例
    ax.set_aspect('equal', adjustable='box')

python 复制代码

if __name__ == '__main__':
    # 创建一个绘图窗口， 宽 15英寸，高 10 英寸
    fig = plt.figure(figsize=(15, 10))
    # 顶部绘制文字，18号，加粗
    fig.suptitle('阶跃函数与sigmoid 函数', fontsize=18, fontweight='bold')

    # 使用GridSpec创建1x2的子图布局
    gs = gridspec.GridSpec(2, 1, figure=fig)

    plot_step_function(gs)

    plot_sigmoid_function(gs)
    # 调整子图间距
    # rect=[0, 0, 1, 0.96] 定义了子图布局的矩形区域：
    # [左, 下, 右, 上] 分别对应矩形区域的边界
    # 0, 0 表示左侧和底部从0开始
    # 1, 0.96 表示右侧到1结束，顶部到0.96结束
    plt.tight_layout(rect=[0, 0, 1, 0.96])

    plt.show()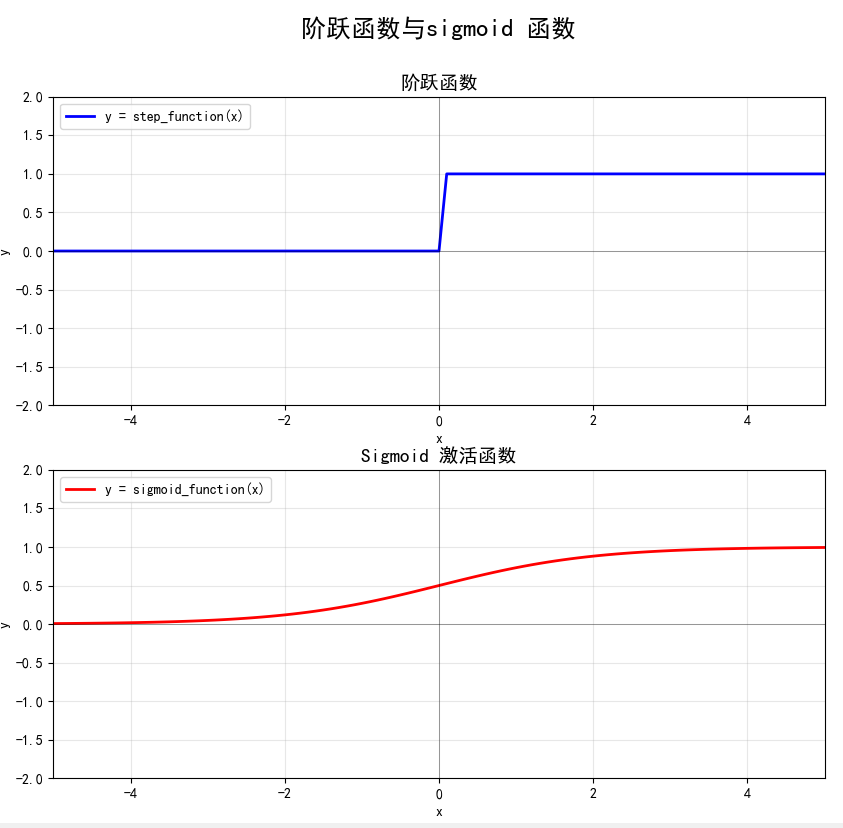

现在我们来比较一下sigmoid 函数和阶跃函数.

是"平滑性"的不同。sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。

于阶跃函数只能返回0或1，sigmoid函数可以返回0_.731 ...、0._880 _..._等实数（这一点和刚才的平滑性有关）。。也就是说，感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号。

下阶跃函数和sigmoid函数具有相似的形状，当输入信号为重要信息时，阶跃函数和sigmoid函数都会输出较大的值；当输入信号为不重要的信息时，两者都输出较小的值。还有一个共同点是，不管输入信号有多小，或者有多大，输出信号的值都在0到1之间。

两者均为非线性函数。sigmoid函数是一条曲线，阶跃函数是一条像阶梯一样的折线，两者都属于非线性的函数。神经网络的激活函数必须使用非线性函数。换句话说，激活函数不能使用线性函数。
函数本来是输入某个值后会返回一个值的转换器。向这个转换器输入某个值后，输出值是输入值的常数倍的函数称为线性函数（用数学式表示为_h_(x) = c_x_。c为常数）。因此，线性函数是一条笔直的直线。而非线性函数，顾名思义，指的是不像线性函数那样呈现出一条直线的函数。

2.3 矩阵乘法

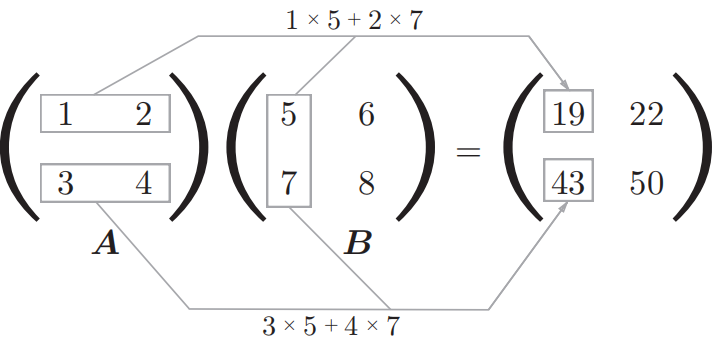
python 复制代码

    A=np.array([[1,2],[3,4]])
    B=np.array([[5,6],[7,8]])
    print(f'A.shape:{A.shape}  B.shape:{B.shape}') # A.shape: (2, 2)  B.shape: (2, 2)
    C=np.dot(A,B)
    print(f'C.shape:{C.shape}') # C.shape: (2, 2)
    print(f'np.matmul:{C}') # np.matmul: [[19 22]
                            #             [43 50]]
    print(f'A*B:{A*B}') # A*B: [[ 5  12]
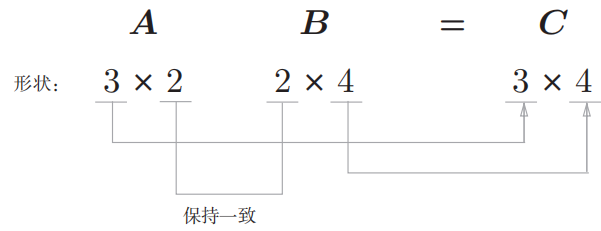
                        #      [21 32]]

再比如 A: 32 矩阵， B: 24 矩阵相乘：

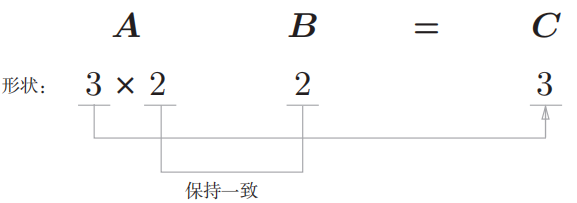
矩阵_A 的第1维的元素个数（列数）必须和矩阵 B 的第0维的元素个数（行数）相等。在上面的例子中，矩阵 **A **_的形状是3 _× 2，矩阵 B _的形状是2 _× 4，矩阵 A 的第1维的元素个数（2）和矩阵 B_的第0维的元素个数（2）相等。如果这两个值不相等，则无法计算矩阵的乘积。

2.4 神经网络内积

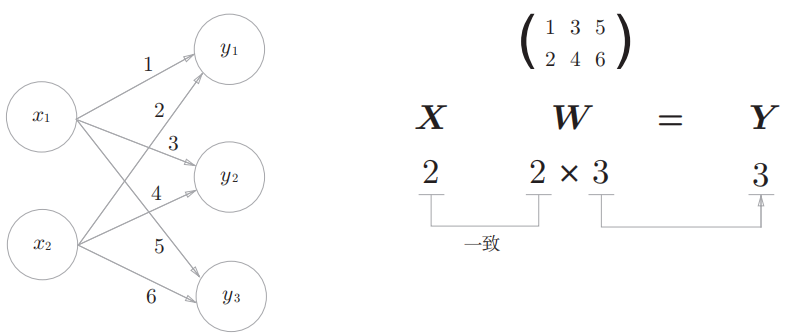
下面我们使用NumPy矩阵来实现神经网络。

python 复制代码

    X=np.array([1,2])
    W=np.array([[1,3,5],[2,4,6]])
    print(f'X.shape:{X.shape}  W.shape:{W.shape}') # X.shape: (2,)  W.shape: (2, 3)
    Y=np.dot(X,W)
    print(f'Y.shape:{Y.shape}  Y:{Y}') #Y.shape:(3,)  Y:[ 5 11 17]

np.dot（多维数组的点积），可以一次性计算出_**Y **的结果。这意味着，即便**Y **_的元素个数为100或1000，也可以通过一次运算就计算出结果

2.5 三层神经网络实现

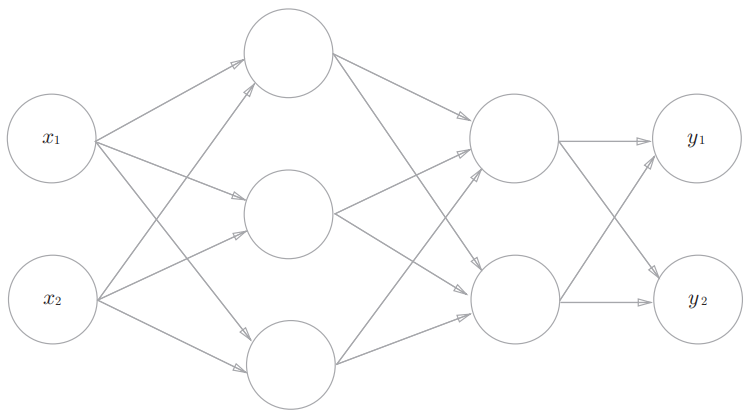
3层神经网络：

输入层(第0层)： 2个神经元
第1层（第1个隐藏层）: 3个神经元
第2层 (第2个隐藏层) : 2 个神经元
输出层(第3层)： 2 个神经元

2.5.1 输入层到第1层的传递

python 复制代码

# X是元素个数为2的一维数组
X=np.array([1.0,0.5])
# 输入是2个神经元，第1层是3个神经元，所以W1是2 × 3的数组
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
# 第1层是3个神经元
B1=np.array([0.1,0.2,0.3])

print(f'X shape:{X.shape}')   # X shape: (2,)
print(f'W1 shape:{W1.shape}') # W1 shape: (2, 3)
print(f'B1 shape:{B1.shape}') # B1 shape: (3,)

A1=np.dot(X,W1)+B1
print(f'A1 shape:{A1.shape}  A1:{A1}') # A1 shape:(3,)  A1:[0.3 0.7 1.1]
Z1=sigmoid(A1)
print(f'Z1 shape:{Z1.shape}  Z1:{Z1}') # Z1 shape:(3,)  Z1:[0.57444252 0.66818777 0.75026011]

2.5.2 第1层到第2层的传递

python 复制代码

# 第1层是3个神经元，第2层是2个神经元，所以W2为 (3,2)
W2=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
# 第2层是2个神经元
B2=np.array([0.1,0.2])

A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)

2.5.3 第2层到第3层的传递

python 复制代码

# 第2层是2个神经元，第3层是2个神经元，所以W3为 (2,2)
W3=np.array([[0.1,0.3],[0.2,0.4]])
# 第3层是2个神经元
B3=np.array([0.1,0.2])

A3=np.dot(Z2,W3)+B3
Z3=sigmoid(A3)

2.5.4 代码实现

将上面的代码进行整理：

初始化网络：数会进行权重和偏置的初始化，并将它们保存在字典变量network中

python 复制代码

def init_network():
    network={} # 创建一个空字典
    # 输入层有1个神经元， 第1层有3个神经元， 所以 w1为2×3的矩阵
    network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    # 第1层有3个神经元,所以 b1为(3,)的列表
    network['b1']=np.array([0.1,0.2,0.3])

    # 第1层有3个神经元，第2层有2个神经元，  所以 W2为3×2的矩阵
    network['W2'] = np.array([[0.1, 0.4],[0.2,0.5], [0.3, 0.6]])
    # 第2层有2个神经元
    network['b2'] = np.array([0.1, 0.2])

    # 第2层有2个神经元，第3层有2个神经元，  所以 W3为2×2的矩阵
    network['W3'] = np.array([[0.1, 0.4],[0.2,0.4]])
    # 第3层有2个神经元
    network['b3'] = np.array([0.1, 0.2])
    return network

信号向前传递

python 复制代码

def identity_function(x):
    return x

def forward(network,x):
    W1,W2,W3=network['W1'],network['W2'],network['W3']
    b1,b2,b3=network['b1'],network['b2'],network['b3']
    A1=np.dot(x,W1)+b1
    Z1=sigmoid(A1)

    A2=np.dot(Z1,W2)+b2
    Z2=sigmoid(A2)

    A3=np.dot(Z2,W3)+b3
    Y=identity_function(A3)
    return Y

主函数

python 复制代码

if __name__ == '__main__':
    # 初始化网络
    network=init_network()
    x=np.array([1.0,0.5])
    # 信号传递
    y=forward(network,x)
    print(y) # [0.31682708 0.75890403]

2.6 输出层设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言：

回归问题：用恒等函数。将输入按原样输出，对于输入的信息，不加以任何改动地直

接输出。

比如，根据一个人的图像预测这个人的体重的问题就是回归问题

分类问题：用softmax函数。是根据某个输入预测一个（连续的）数值的问题。

比如，区分图像中的人是男性还是女性的问题就是分类问题.

softmax函数的作用是将向量 a=[a1,a2,...,an]a =[_a_1,_a_2,...,a__n] 转换为概率分布,

y_k 表示第 k__个类别的概率。

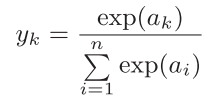
exp(x )是表示e^*x*_ _的指数函数(e是常数 2.7182...)

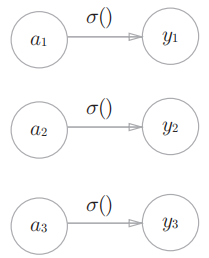
输出层共有 n个神经元，计算第k 个神经元的输出 y_k

python 复制代码

def softmax(a):
    '''
    假设 a =np.array([0.3,2.9,4.0])
    :param a:
    :return:
    '''
    # 分子：输入信号ak的指数函数
    exp_a=np.exp(a)  # [ 1.34985881 18.17414537 54.59815003]
    # 分母: 输入信号指数函数的和
    sum_exp_a=np.sum(exp_a) # 74.1221542102
    y=exp_a/sum_exp_a  # [ 0.01821127 0.24519181 0.73659691]
    return y

softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。比如，e¹⁰的值

会超过20000，e¹⁰⁰会变成一个后面有40多个0的超大值. 如果在这些超大值之间进行除法运算，结果会出现"不确定"的情况. 下面是改进的版本。

python 复制代码

def softmax(a):
    '''
    假设 a =np.array([0.3,2.9,4.0])
    :param a:
    :return:
    '''
    c=np.max(a)
    exp_a=np.exp(a-c) # 溢出对策
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a  # [ 0.01821127 0.24519181 0.73659691]
    return y

softmax函数的输出是0_.0到1._0之间的实数。并且，softmax 函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以把softmax函数的输出解释为"概率"。

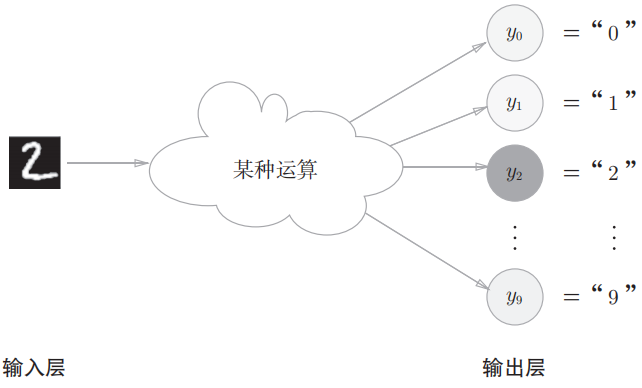
输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。比如识别手写数字：

二、什么是深度学习？（Deep Learning）

如果神经网络只有 1~2 个隐藏层，叫浅层网络
如果有 3 层或更多隐藏层 ，就叫深度神经网络（DNN） ，这种学习方法就叫 深度学习

"深度" = 网络层数多，能逐层提取更抽象的特征

识别一张猫的照片：

第1层：检测边缘（横线、竖线、曲线）
第2层：组合边缘 → 圆形（眼睛）、三角形（耳朵）
第3层：组合形状 → 脸部结构
第4层：识别出"这是猫的脸"
最后：输出"猫"的概率

深度学习是神经网络的一个子集，但因为效果太强，现在几乎成了主流。

三、三种神经网络模型

3.1 ANN（Artificial Neural Network）------人工神经网络

最基础的"大脑模型"，就像人脑中有神经元互相连接，ANN 是由很多"人工神经元"组成的网络。

通常分为三层：

输入层（接收数据，比如一张图片的像素值）
隐藏层（中间处理信息，可以有多层）
输出层（给出结果，比如"这是猫"或"这是狗"）

适合处理结构化数据 ，比如表格数据（房价预测、客户分类等），如果直接用 ANN 处理图像或语音，效果不好，因为没考虑数据的空间结构

3.2 CNN（Convolutional Neural Network）------卷积神经网络

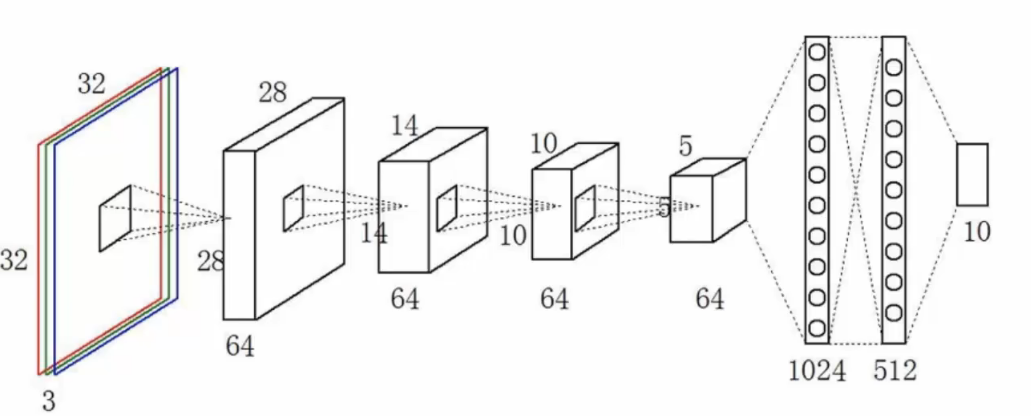
门看"图像"的专家，用"小窗口"（叫卷积核）在图像上滑动，提取局部特征（比如边缘、纹理、形状）

第一层可能识别边缘
第二层组合边缘成简单形状（如圆形、角）
更深层能识别复杂物体（如眼睛、耳朵、整张脸）

它有三个关键操作：

卷积（Convolution）：提取特征
池化（Pooling）：压缩信息，保留重点（比如取最大值）
全连接层：最后做分类

CNN 像一个"显微镜+拼图高手"，先看局部细节，再拼出整体含义。

3.3 RNN（Recurrent Neural Network）------循环神经网络

擅长处理"有顺序"的数据，有些数据是有时间顺序 或上下文依赖的，比如：

一句话："我今天吃了一个 ___" → 下一个词很可能是"苹果"而不是"汽车"
股票价格、天气预测、语音信号......

它有一个"记忆"机制------当前输出不仅取决于当前输入，还记住之前的信息。想象一个神经元在时间上"循环使用自己"，每次输入新数据时，都带着上次的记忆。

网络对比

模型	全称	擅长处理	核心思想	典型应用
ANN	人工神经网络	结构化数据（表格）	多层神经元前向传播	房价预测、分类
CNN	卷积神经网络	图像、网格数据	局部感知 + 权重共享	图像识别、目标检测
RNN	循环神经网络	序列数据（文本、语音）	带记忆的循环结构	翻译、聊天机器人